Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Impagliazzo, Russell
and
Krajíček, Jan
2002.
A Note on Conservativity Relations among Bounded Arithmetic Theories.
MLQ,
Vol. 48,
Issue. 3,
p.
375.
Hanika, Jiří
2004.
Herbrandizing search problems in Bounded Arithmetic.
Mathematical Logic Quarterly,
Vol. 50,
Issue. 6,
p.
577.
Skelley, Alan
2004.
Computer Science Logic.
Vol. 3210,
Issue. ,
p.
340.
Buresh-Oppenheim, J.
and
Morioka, T.
2004.
Relativized NP search problems and propositional proof systems.
p.
54.
Beckmann, Arnold
and
Johannsen, Jan
2005.
An unexpected separation result in Linearly Bounded Arithmetic.
MLQ,
Vol. 51,
Issue. 2,
p.
191.
Cook, Stephen
and
Morioka, Tsuyoshi
2005.
Quantified propositional calculus and a second-order theory for NC1.
Archive for Mathematical Logic,
Vol. 44,
Issue. 6,
p.
711.
Beyersdorff, Olaf
2009.
On the correspondence between arithmetic theories and propositional proof systems – a survey.
Mathematical Logic Quarterly,
Vol. 55,
Issue. 2,
p.
116.
Thapen, Neil
2011.
Higher complexity search problems for bounded arithmetic and a formalized no-gap theorem.
Archive for Mathematical Logic,
Vol. 50,
Issue. 7-8,
p.
665.
Atserias, Albert
and
Thapen, Neil
2014.
The Ordering Principle in a Fragment of Approximate Counting.
ACM Transactions on Computational Logic,
Vol. 15,
Issue. 4,
p.
1.
Beckmann, Arnold
and
Razafindrakoto, Jean-José
2017.
Logic, Language, Information, and Computation.
Vol. 10388,
Issue. ,
p.
31.
Pudlák, Pavel
2017.
Logic Colloquium '03.
p.
244.
Krajíček, Jan
2019.
Proof Complexity.
Pudlák, Pavel
and
Thapen, Neil
2019.
Random resolution refutations.
computational complexity,
Vol. 28,
Issue. 2,
p.
185.
Jeřábek, Emil
2020.
Induction rules in bounded arithmetic.
Archive for Mathematical Logic,
Vol. 59,
Issue. 3-4,
p.
461.
Kołodziejczyk, Leszek Aleksander
and
Thapen, Neil
2022.
Approximate counting and NP search problems.
Journal of Mathematical Logic,
Vol. 22,
Issue. 03,
Korten, Oliver
and
Pitassi, Toniann
2024.
Strong vs. Weak Range Avoidance and the Linear Ordering Principle.
p.
1388.
 -definable with small i (i = 1, 2, 3) in fragments of bounded arithmetic T2 in terms of natural search problems defined over polynomial-time structures. We obtain the following results:
-definable with small i (i = 1, 2, 3) in fragments of bounded arithmetic T2 in terms of natural search problems defined over polynomial-time structures. We obtain the following results: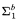 and
and 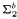 -definable in the theories
-definable in the theories 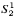 and
and 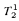 .
.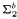 and
and 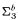 -definable in the theory
-definable in the theory 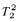 .
.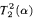 is not
is not 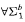 -conservative over the theory
-conservative over the theory 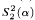 .
.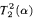 is not
is not 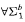 -conservative over the theory
-conservative over the theory 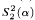 , we present two examples of a
, we present two examples of a 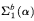 -principle separating the two theories:
-principle separating the two theories: