No CrossRef data available.
Article contents
Weakly compact cardinals in models of set theory
Published online by Cambridge University Press: 12 March 2014
Extract
The central notion of this paper is that of a κ-elementary end extension of a model of set theory. A model 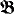 is said to be a κ-elementary end extension of a model
is said to be a κ-elementary end extension of a model 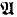 of set theory if
of set theory if 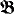 >
> 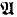 and κ, which is a cardinal of
and κ, which is a cardinal of 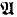 , is end extended in the passage from
, is end extended in the passage from 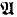 to
to 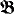 , i.e.,
, i.e., 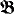 enlarges κ without enlarging any of its members (see §0 for more detail). This notion was implicitly introduced by Scott in [Sco] and further studied by Keisler and Morley in [KM], Hutchinson in [H] and recently by the author in [E]. It is not hard to see that if
enlarges κ without enlarging any of its members (see §0 for more detail). This notion was implicitly introduced by Scott in [Sco] and further studied by Keisler and Morley in [KM], Hutchinson in [H] and recently by the author in [E]. It is not hard to see that if 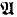 has a κ-elementary end extension then κ must be regular in
has a κ-elementary end extension then κ must be regular in 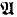 . Keisler and Morley [KM] noticed that this has a converse if
. Keisler and Morley [KM] noticed that this has a converse if 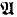 is countable, i.e., if κ is a regular cardinal of a countable model
is countable, i.e., if κ is a regular cardinal of a countable model 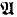 then
then 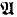 has a κ-elementary end extension. Later Hutchinson [H] refined this result by constructing κ-elementary end extensions
has a κ-elementary end extension. Later Hutchinson [H] refined this result by constructing κ-elementary end extensions 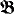 1 and
1 and 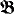 2 of an arbitrary countable model
2 of an arbitrary countable model 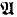 in which κ is a regular uncountable cardinal, such that
in which κ is a regular uncountable cardinal, such that 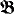 1 adds a least new element to κ while
1 adds a least new element to κ while 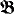 2 adds no least new ordinal to κ. It is a folklore fact of model theory that the Keisler-Morley result gives soft and short proofs of countable compactness and abstract completeness (i.e. recursive enumera-bility of validities) of the logic L(Q), studied extensively in Keisler's [K2]; and Hutchinson's refinement does the same for stationary logic L(aa), studied by Barwise et al. in [BKM]. The proof of Keisler-Morley and that of Hutchinson make essential use of the countability of
2 adds no least new ordinal to κ. It is a folklore fact of model theory that the Keisler-Morley result gives soft and short proofs of countable compactness and abstract completeness (i.e. recursive enumera-bility of validities) of the logic L(Q), studied extensively in Keisler's [K2]; and Hutchinson's refinement does the same for stationary logic L(aa), studied by Barwise et al. in [BKM]. The proof of Keisler-Morley and that of Hutchinson make essential use of the countability of 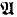 since they both rely on the Henkin-Orey omitting types theorem. As pointed out in [E, Theorem 2.12], one can prove these theorems using “generic” ultrapowers just utilizing the assumption of countability of the
since they both rely on the Henkin-Orey omitting types theorem. As pointed out in [E, Theorem 2.12], one can prove these theorems using “generic” ultrapowers just utilizing the assumption of countability of the 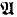 -power set of κ. The following result, appearing as Theorem 2.14 in [E], links the notion of κ-elementary end extension to that of measurability of κ. The proof using (b) is due to Matti Rubin.
-power set of κ. The following result, appearing as Theorem 2.14 in [E], links the notion of κ-elementary end extension to that of measurability of κ. The proof using (b) is due to Matti Rubin.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1985


