Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2025-01-03T10:32:09.605Z Has data issue: false hasContentIssue false
  • English
  • Français

Weakly atomic-compact relational structures

Published online by Cambridge University Press:  12 March 2014

G. Fuhrken  and
W. Taylor
G. Fuhrken
Affiliation:
University of Minnesota, Minneapolis, Minnesota 55455
W. Taylor
Affiliation:
University of Colorado, Boulder, Colorado 80302
Get access Rights & Permissions [Opens in a new window]

Extract

A relational structure 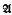is called weakly atomic-compact if and only if every set Σ of atomic formulas (taken from the first-order language of the similarity type of 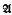augmented by a possibly uncountable set of additional variables as “unknowns”) is satisfiable in 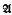whenever every finite subset of Σ is so satisfiable. This notion (as well as some related ones which will be mentioned in §4) was introduced by J. Mycielski as a generalization to model theory of I. Kaplansky's notion of an algebraically compact Abelian group (cf. [5], [7], [1], [8]).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 36 , Issue 1 , March 1971 , pp. 129 - 140
Copyright
Copyright © Association for Symbolic Logic 1971

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Balcerzyk, S., On algebraically compact groups of I. Kaplansky, Fundamenta Mathematicae, vol. 44 (1957), pp. 91–93.CrossRefGoogle Scholar
[2]Engeler, E., Äquivalenzklassen von n-Tupeln, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 5 (1959), pp. 340–345.CrossRefGoogle Scholar
[3]Erdös, P. and Rado, R., A partition calculus in set theory, Bulletin of the American Mathematical Society, vol. 62 (1956), pp. 427–489.CrossRefGoogle Scholar
[4]Grätzer, G. and Lakser, H., Equationally compact semilattices, Colloquium Mathematicum, vol. 20 (1969), pp. 27–30.CrossRefGoogle Scholar
[5]Kaplansky, I., Infinite Abelian groups, University of Michigan Press, Ann Arbor, Michigan, 1954.Google Scholar
[6]Karp, C. R., Languages with expressions of infinite length, North-Holland, Amsterdam, 1964.Google Scholar
[7]Łoś, J., Abelian groups that are direct summands of every abelian group which contains them as pure subgroups, Fundamenta Mathematicae, vol. 44 (1957), pp. 84–90.CrossRefGoogle Scholar
[8]Mycielski, J., Some compactifications of general algebras, Colloquium Mathematicum, vol. 13 (1964), pp. 1–9.CrossRefGoogle Scholar
[9]Mycielski, J. and Ryll-Nardzewski, C., Equationally compact algebras (II), Fundamenta Mathematicae, vol. 61 (1968), pp. 271–281. Errata vol. 62 (1968), p. 309.CrossRefGoogle Scholar
[10]Orey, S., On ω-consistency and related properties, this Journal, vol. 21 (1956), pp. 246–252.Google Scholar
[11]Ramsey, F. P., On a problem in formal logic, Proceedings of the London Mathematical Society (2), vol. 30 (1930), pp. 264–286.CrossRefGoogle Scholar
[12]Rasiowa, H. and Sikorski, R., A proof of the completeness theorem of Gödel, Fundamenta Mathematicae, vol. 37 (1950), pp. 193–200.CrossRefGoogle Scholar
[13]Rosser, J. B., Gödel theorems for nonconstructive logics, this Journal, vol. 2 (1937), pp. 129–137.Google Scholar
[14]Ryll-Nardzewski, C., On theories categorical in power ≥ℵ0, Bulletin de l'Académie Polonaise des Sciences, Série des sciences mathématiques, astronomiques et physiques, vol. 7 (1959), pp. 545–548.Google Scholar
[15]Taylor, W., Atomic compactness and elementary equivalence, Fundamenta Mathematicae vol. 71 (1971) (to appear).CrossRefGoogle Scholar
[16]Taylor, W., Compact models, Abstract 69T-E74, Notices of the American Mathematical Society, vol. 16 (1969), p. 980.Google Scholar
[17]Trakhtenbrot, B. A., The impossibility of an algorithm for the decision problem in finite classes (Russian), Doklady Akadémii Nauk SSSR, vol. 70 (1950), pp. 569–572.Google Scholar
[18]Vaught, R. L., Denumerable models of complete theories, Proceedings of the Symposium on the foundations of mathematics, infinitistic methods, Warsaw, Pergamon Press, Kraków, 1961, pp. 303–321.Google Scholar
[19]Węglorz, B., Equationally compact algebras (I), Fundamenta Mathematicae, vol. 59 (1966), pp. 289–298.CrossRefGoogle Scholar
[20]Węglorz, B., Equationally compact algebras (III), Fundamenta Mathematicae, vol. 60 (1967), pp. 89–93.CrossRefGoogle Scholar