Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-23T12:07:48.876Z Has data issue: false hasContentIssue false
  • English
  • Français

WEAK REFLECTION PRINCIPLE, SATURATION OF THE NONSTATIONARY IDEAL ON ω1 AND DIAMONDS

Published online by Cambridge University Press:  19 June 2017

VÍCTOR TORRES-PÉREZ
VÍCTOR TORRES-PÉREZ*
Affiliation:
INSTITUT FÜR DISKRETE MATHEMATIK UND GEOMETRIE, TU WIEN WIEDNER HAUPSTRASSE 8/104 1040 VIENNA, AUSTRIAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that WRP and saturation of the ideal NSω1 together imply 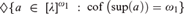$\left\{ {a \in [\lambda ]^{\omega _1 } :{\text{cof}}\left( {{\text{sup}}\left( a \right)} \right) = \omega _1 } \right\}$, for every cardinal λ with cof(λ) ≥ω2 .

Keywords

03E0503E1003E65Weak Reflection Principlesaturation of idealsdiamond principlescardinal arithmetic
Type
Articles
Information
The Journal of Symbolic Logic , Volume 82 , Issue 2 , June 2017 , pp. 724 - 736
Copyright
Copyright © The Association for Symbolic Logic 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Donder, H.-D. and Matet, P., Two cardinal versions of diamond . Israel Journal of Mathematics, vol. 83 (1993), no. 1–2, pp. 1–43.CrossRefGoogle Scholar
Feng, Q. and Jech, T., Local clubs, reflection, and preserving stationary sets . Proceedings of the London Mathematical Society (3), vol. 58 (1989), no. 2, pp. 237–257.Google Scholar
Foreman, M., Magidor, M., and Shelah, S., Martin’s maximum, saturated ideals, and nonregular ultrafilters . I. Annals of Mathematical (2), vol. 127 (1988), no. 1, pp. 1–47.Google Scholar
Foreman, M. and Todorcevic, S., A new Löwenheim-Skolem theorem. Transactions of the American Mathematical Society, vol. 357 (2005 ), no. 5, pp. 1693–1715 (electronic).Google Scholar
Holz, M., Steffens, K., and Weitz, E., Introduction to Cardinal Arithmetic, Birkhäuser Advanced Texts: Basler Lehrbücher, Birkhäuser Verlag, Basel, 1999.Google Scholar
Jech, T., Some combinatorial problems concerning uncountable cardinals . Annals of Mathematical Logic, vol. 5 (1972/73), pp. 165–198.Google Scholar
Jech, T., Set Theory, Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003. The third millennium edition, revised and expanded.Google Scholar
Jech, T., Stationary sets , Handbook of Set Theory (Foreman, M. and Kanamori, A., editors), Springer, Netherlands, 2010, pp. 93–128.Google Scholar
Jech, T. and Prikry, K., On ideals of sets and the power set operation. Bulletin of the American Mathematical Society, vol. 82 (1976), no. 4, pp. 593–595.Google Scholar
Jech, T. and Prikry, K., Ideals over uncountable sets: Application of almost disjoint functions and generic ultrapowers . Memoirs of the American Mathematical Society, vol. 18 (1979), no. 214.Google Scholar
Kunen, K., Set Theory, Studies in Logic and the Foundations of Mathematics, vol. 102, North-Holland, Amsterdam-New York, 1980.Google Scholar
Levy, J., Principes de réflexion et codages et la structure H ω 2 . Ph.D. thesis, Université Paris Diderot Paris 7, 2006.Google Scholar
Matet, P., Game ideals . Annals of Pure and Applied Logic, vol. 158 (2009), no. 1–2, pp. 23–39.Google Scholar
Namba, K., Independence proof of (ω, ω α) -distributive law in complete Boolean algebras . Commentarii mathematici Universitatis Sancti Pauli, vol. 19 (1971), pp. 1–12.Google Scholar
Namba, K., (ω 1, 2)-distributive law and perfect sets in generalized Baire space . Commentarii mathematici Universitatis Sancti Pauli, vol. 20 (1971/72), pp. 107–126.Google Scholar
Shelah, S., An $\aleph _2 $ Souslin tree from a strange hypothesis . Abstracts of Papers Presented to the American Mathematical Society, vol. 160 (1984), pp. 198.Google Scholar
Shelah, S., Advances in cardinal arithmetic , Finite and Infinite Combinatorics in Sets and Logic (Banff, AB, 1991), NATO Advanced Science Institutes Series C: Mathematical and Physical Sciences, Kluwer Academic Publishers, Dordrecht, 1993, pp. 355–383.Google Scholar
Shelah, S., Cardinal Arithmetic, Oxford Logic Guides, vol. 29, The Clarendon Press, Oxford University Press, Oxford Science Publications, New York, 1994.CrossRefGoogle Scholar
Shelah, S., Reflection implies the SCH . Fundamenta Mathematicae, vol. 198 (2008), no. 2, pp. 95–111.Google Scholar
Shelah, S., Diamonds . Proceedings of the American Mathematical Society, vol. 138 (2010), no. 6, pp. 2151–2161.Google Scholar
Shioya, M., Diamonds on $P_\kappa \lambda $ Computational Prospects of Infinity. Part II. Presented Talks (Chong, C., Feng, Q., Slaman, T. A., Hugh Woodin, W., and Yang, Y., editors), Lecture Notes Series, Institute for Mathematical Sciences, National University of Singapore, vol. 15, World Scientific Publishing, Hackensack, NJ, 2008, pp. 271–298.Google Scholar
Todorčević, S., Reflecting stationary sets , handwritten notes, October 1988.Google Scholar
Todorčević, S., Localized reflection and fragments of PFA , Set Theory (Piscataway, NJ, 1999) (Thomas, S., editor), DIMACS Series in Discrete Mathematics and Theoretical Computer Science, vol. 58, American Mathematical Society, Providence, RI, 2002, pp. 135–148.CrossRefGoogle Scholar
Todorčević, S. and Torres-Pérez, V., Rado’s conjecture and ascent paths of square sequences . Mathematical Logic Quarterly, vol. 60 (2014), no. 1–2, pp. 84–90.Google Scholar
Torres-Pérez, V., Réflexion, compacité et arithmétique des cardinaux. Ph.D. thesis, Université Paris Diderot Paris 7, 2009.Google Scholar
Veličković, B., Forcing axioms and stationary sets . Advances in Mathematics, vol. 94 (1992), no. 2, pp. 256–284.Google Scholar
Woodin, W. H.. The Axiom of Determinacy, Forcing Axioms, and the Nonstationary Ideal, de Gruyter Series in Logic and its Applications, vol. 1, Walter de Gruyter & Co., Berlin, 1999.Google Scholar