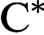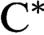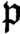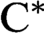Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bhat, B.V. Rajarama
and
Kumar, Manish
2022.
C⁎-extreme maps and nests.
Journal of Functional Analysis,
Vol. 282,
Issue. 8,
p.
109397.