Published online by Cambridge University Press: 12 March 2014
We introduce a very weak language 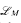 on p-adic fields K, which is just rich enough to have exactly the same definable subsets of the line K that one has using the ring language. (In our context, definable always means definable with parameters.) We prove that the only definable functions in the language
on p-adic fields K, which is just rich enough to have exactly the same definable subsets of the line K that one has using the ring language. (In our context, definable always means definable with parameters.) We prove that the only definable functions in the language 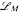 are trivial functions. We also give a definitional expansion
are trivial functions. We also give a definitional expansion 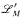 of
of 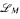 in which K has quantifier elimination, and we obtain a cell decomposition result for
in which K has quantifier elimination, and we obtain a cell decomposition result for 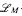 -definable sets.
-definable sets.
Our language 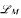 can serve as a p-adic analogue of the very weak language (<) on the real numbers, to define a notion of minimality on the field of p-adic numbers and on related valued fields. These fields are not necessarily Henselian and may have positive characteristic.
can serve as a p-adic analogue of the very weak language (<) on the real numbers, to define a notion of minimality on the field of p-adic numbers and on related valued fields. These fields are not necessarily Henselian and may have positive characteristic.