Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-19T02:56:11.971Z Has data issue: false hasContentIssue false
  • English
  • Français

The Veblen functions for computability theorists

Published online by Cambridge University Press:  12 March 2014

Alberto Marcone  and
Antonio Montalbán
Alberto Marcone
Affiliation:
Dipartimento di Matematica e Informatica, Università di Udine33100 Udine, Italy, E-mail: [email protected]
Antonio Montalbán
Affiliation:
Department of Mathematics, University of Chicago, Chicago, Il 60637, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

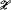We study the computability-theoretic complexity and proof-theoretic strength of the following statements: (1) “If is a well-ordering, then so is 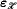”, and (2) “If 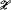is a well-ordering, then so is φ(α, 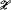)”, where ∝ is a fixed computable ordinal and φ represents the two-placed Veblen function. For the former statement, we show that ω iterations of the Turing jump are necessary in the proof and that the statement is equivalent to 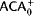over RCA0. To prove the latter statement we need to use ωα iterations of the Turing jump, and we show that the statement is equivalent to 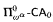. Our proofs are purely computability-theoretic. We also give a new proof of a result of Friedman: the statement “if 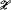is a well-ordering, then so is φ(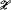, 0)” is equivalent to ATR0 over RCA0.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 76 , Issue 2 , June 2011 , pp. 575 - 602
Copyright
Copyright © Association for Symbolic Logic 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Afs08]Afshari, Bahareh, Relative computability and the proof-theoretic strength of some theories, Ph.D. thesis, University of Leeds, 2008.Google Scholar
[AR09]Afshari, Bahareh and Rathjen, Michael, Reverse mathematics and well-ordering principles: A pilot study, Annals of Pure and Applied Logic, vol. 160 (2009), no. 3, pp. 231–237.CrossRefGoogle Scholar
[BHS87]Blass, Andreas R., Hirst, Jeffry L., and Simpson, Stephen G., Logical analysis of some theorems of combinatorics and topological dynamics, Logic and combinatorics (Simpson, Stephen G., editor), American Mathematical Society, Providence, R.I., 1987, pp. 125–156.CrossRefGoogle Scholar
[Can97]Cantor, Georg, Beiträge zur Begründung der transfiniten Mengenlehre, Mathematische Annalen, vol. 49 (1897), no. 2, pp. 207–246.CrossRefGoogle Scholar
[Fef64]Feferman, Solomon, Systems of predicative analysis, this Journal, vol. 29 (1964), pp. 1–30.Google Scholar
[FMS82]Friedman, Harvey, Mcaloon, Kenneth, and Simpson, Stephen G., A finite combinatorial principle which is equivalent to the 1-consistency of predicative analysis, Patras Logic Symposion (Metakides, George, editor), North-Holland, Amsterdam, 1982, pp. 197–230.CrossRefGoogle Scholar
[FMW]Friedman, Harvey, Montalbán, Antonio, and Weiermann, Andreas, A characterization of ATR0 in terms of a Kruskal-like tree theorem, unpublished draft.Google Scholar
[Gen36]Gentzen, Gerhard, Die Widerspruchsfreiheit der reinen Zahlentheorie, Mathematische Annalen, vol. 112 (1936), no. 1, pp. 493–565.CrossRefGoogle Scholar
[Gir87]Girard, Jean-Yves, Proof theory and logical complexity, Bibliopolis, Naples, 1987.Google Scholar
[Hir94]Hirst, Jeffry L., Reverse mathematics and ordinal exponentiation, Annals of Pure and Applied Logic, vol. 66 (1994), no. 1, pp. 1–18.CrossRefGoogle Scholar
[MM09]Marcone, Alberto and Montalbán, Antonio, On Fraïssé's conjecture for linear orders of finite Hausdorff rank, Annals of Pure and Applied Logic, vol. 160 (2009), no. 3, pp. 355–367.CrossRefGoogle Scholar
[McA85]Mcaloon, Kenneth, Paris-Harrington incompleteness and progressions of theories. Proceedings of the AMS-ASL summer institute held in Ithaca, N.Y., June 28–July 16, 1982 (Nerode, Anil and Shore, Richard A., editors), Proceedings of Symposia in Pure Mathematics, vol. 42, American Mathematical Society, Providence, RI, 1985, pp. 447–460.Google Scholar
[Rat91]Rathjen, Michael, The role of parameters in bar rule and bar induction, this Journal, vol. 56 (1991), no. 2, pp. 715–730.Google Scholar
[Rat06]Rathjen, Michael, The art of ordinal analysis, International Congress of Mathematicians. Vol. II, European Mathematical Society, Zürich, 2006, pp. 45–69.Google Scholar
[RW11]Rathjen, Michael and Weiermann, Andreas, Reverse mathematics and well-ordering principles, Computability in Context: Computation and Logic in the Real World (Cooper, S. B. and Sorbi, A., editors), World Scientific, 2011.Google Scholar
[Sch77]Schütte, Kurt, Proof theory, Grundlehren der Mathematischen Wissenschaften, vol. 225, Springer-Verlag, Berlin, 1977.CrossRefGoogle Scholar
[Sho06]Shore, Richard A., Invariants, Boolean algebras and , Transactions of the American Mathematical Sodety, vol. 358 (2006), no. 3, pp. 989–1014.CrossRefGoogle Scholar
[Sim99]Simpson, Stephen G., Subsystems of second order arithmetic, Springer, 1999.CrossRefGoogle Scholar
[Veb08]Veblen, Oswald, Continuous increasing functions of finite and transfinite ordinals. Transactions of the American Mathematical Society, vol. 9 (1908), no. 3, pp. 280–292.CrossRefGoogle Scholar