Article contents
Vaught's theorem recursively revisited1
Published online by Cambridge University Press: 12 March 2014
Extract
In this paper we investigate the relationship between the number of countable and decidable models of a complete theory. The number of decidable models will be determined in two ways, in §1 with respect to abstract isomorphism type, and in §2 with respect to recursive isomorphism type.
Definition 1. A complete theory is (α, β) if the number of countable models of T, up to abstract isomorphism, is β, and similarly the number of decidable models of T is α.
Definition 2. A model 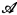 is ω-decidable if ∣
is ω-decidable if ∣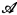 ∣= ω and for an effective listing {θn∣n < ω} of all sentences in the language of Th(
∣= ω and for an effective listing {θn∣n < ω} of all sentences in the language of Th(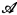 ) augmented by new constant symbols i*, i < ω, {n ∣〈
) augmented by new constant symbols i*, i < ω, {n ∣〈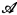 , i〉i<ω ⊨ θn} is recursive, where i interprets i* (in these terms,
, i〉i<ω ⊨ θn} is recursive, where i interprets i* (in these terms, 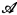 is decidable if
is decidable if 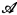 is abstractly isomorphic to an ω-decidable model).
is abstractly isomorphic to an ω-decidable model).
Definition 3. A complete theory is (α, β)r if it is (γ, β) for some γ and it has exactly αω-decidable models up to recursive isomorphism.
Specifically we will show in §1 that there is a (2, ω) theory, and in §2 that although there is a (2, 2ω) theory, there is no (2, β)r theory for any β, β < 2ω.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1981
Footnotes
The preparation of this paper was partially supported by Grant NSF-MCS 77-00802.
References
REFERENCES
- 6
- Cited by


