Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2025-01-05T14:30:10.767Z Has data issue: false hasContentIssue false
  • English
  • Français

The upper semilattice of degrees ≤ 0′ is complemented

Published online by Cambridge University Press:  12 March 2014

David B. Posner
David B. Posner*
Affiliation:
San Jose State University, San Jose, California 95192
Get access Rights & Permissions [Opens in a new window]

Extract

Let 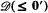denote the set of degrees ≤ 0′. A degree a ≤ 0′ is said to be complemented in 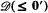if there exists a degree b ≤ 0′ such that b ∪ a = 0′ and b ∩ a = 0. R.W. Robinson (cf. [11]) showed that every degree a ≤ 0′ satisfying a″ = 0″ is complemented in 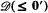and the author [8] showed that every degree a ≤ 0′ satisfying a′ = 0″ is complemented in 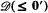. Also, in [2], R. L. Epstein showed that every r.e. degree is complemented in 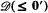. In this paper we will show that in fact every degree ≤ 0′ is complemented in 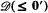. We will further show that the same is true in the upper semilattice of degrees ≤ c, where c is any complete degree. This is in contrast to the situation in the upper semilattice of r.e. degrees in which, as Lachlan [6] has shown, no degree other than 0 and 0′ is complemented.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 46 , Issue 4 , December 1981 , pp. 705 - 713
Copyright
Copyright © Association for Symbolic Logic 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Cooper, S. B., Minimal degrees and the jump operator, this Journal, vol. 38 (1973), pp. 249–271.Google Scholar
[2]Epstein, R. L., Minimal degrees of unsohability and the full approximation construction, Memoirs of the American Mathematical Society, No. 162, American Mathematical Society, Providence, RI, 1975.Google Scholar
[3]Jockusch, C., Degrees in which the recursive sets are uniformly recursive, Canadian Journal of Mathematics, vol. 24 (1972), pp. 1092–1099.CrossRefGoogle Scholar
[4]Jockusch, C., Simple proofs of some theorems on high degrees, Canadian Journal of Mathematics, vol. 29, no. 5 (1977), pp. 1072–1080.CrossRefGoogle Scholar
[5]Jockusch, C. and Posner, D., Double jumps of minimal degrees, this Journal, vol. 43 (1978), pp. 715–524.Google Scholar
[6]Lachlan, A. H., The impossibility of finding relative complements for recursively enumerable degrees, this Journal, vol. 31 (1966), pp. 434–454.Google Scholar
[7]Miller, W. and Martin, D., The degrees of hyperimmune sets, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 14 (1968).CrossRefGoogle Scholar
[8]Posner, D., High degrees, Doctoral Dissertation, University of California, Berkeley, 1977.Google Scholar
[9]Posner, D., Minimal degrees and high degrees (to appear).Google Scholar
[10]Posner, D., Joins and complements below high degrees (to appear).Google Scholar
[11]Posner, D. and Robinson, R. W., Degrees joining to 0′, this Journal, vol. 46 (1981), pp. 714–722.Google Scholar
[12]Shoenfield, J., On degrees of unsohability, Annals of Mathematics, vol. 69 (1959), pp. 644–653.CrossRefGoogle Scholar
[13]Shoenfield, J., Degrees of unsohability, North-Holland, Amsterdam, 1971.Google Scholar