Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Shelah, Saharon
2003.
Logical dreams.
Bulletin of the American Mathematical Society,
Vol. 40,
Issue. 2,
p.
203.
Džamonja, Mirna
and
Shelah, Saharon
2004.
On ◁∗-maximality.
Annals of Pure and Applied Logic,
Vol. 125,
Issue. 1-3,
p.
119.
Larson, Jean A.
2005.
Ramsey Theory for Countable Binary Homogeneous Structures.
Notre Dame Journal of Formal Logic,
Vol. 46,
Issue. 3,
Kojman, Menachem
and
Shelah, Saharon
2006.
Almost isometric embedding between metric spaces.
Israel Journal of Mathematics,
Vol. 155,
Issue. 1,
p.
309.
Fuchino, Sakae
Greenberg, Noam
and
Shelah, Saharon
2006.
Models of real-valued measurability.
Annals of Pure and Applied Logic,
Vol. 142,
Issue. 1-3,
p.
380.
Thompson, Katherine
2010.
Small universal families for graphs omitting cliques without GCH.
Archive for Mathematical Logic,
Vol. 49,
Issue. 7-8,
p.
799.
Džamonja, Mirna
2013.
Logic and Its Applications.
Vol. 7750,
Issue. ,
p.
17.
Motto Ros, Luca
2013.
The descriptive set-theoretical complexity of the embeddability relation on models of large size.
Annals of Pure and Applied Logic,
Vol. 164,
Issue. 12,
p.
1454.
GARTI, Shimon
and
SHELAH, Saharon
2014.
Partition calculus and cardinal invariants.
Journal of the Mathematical Society of Japan,
Vol. 66,
Issue. 2,
Davis, Jacob
2017.
Universal graphs at ℵω1+1.
Annals of Pure and Applied Logic,
Vol. 168,
Issue. 10,
p.
1878.
Brooke-Taylor, A.D.
Fischer, V.
Friedman, S.D.
and
Montoya, D.C.
2017.
Cardinal characteristics at κ in a small u(κ) model.
Annals of Pure and Applied Logic,
Vol. 168,
Issue. 1,
p.
37.
Cummings, James
Džamonja, Mirna
Magidor, Menachem
Morgan, Charles
and
Shelah, Saharon
2017.
A framework for forcing constructions at successors of singular cardinals.
Transactions of the American Mathematical Society,
Vol. 369,
Issue. 10,
p.
7405.
Džamonja, Mirna
and
Panza, Marco
2018.
Contradictions, from Consistency to Inconsistency.
Vol. 47,
Issue. ,
p.
159.
Shelah, Saharon
2021.
Divide and Conquer: Dividing Lines and Universality.
Theoria,
Vol. 87,
Issue. 2,
p.
259.
Poveda, Alejandro
Rinot, Assaf
and
Sinapova, Dima
2021.
Sigma-Prikry forcing I: The Axioms.
Canadian Journal of Mathematics,
Vol. 73,
Issue. 5,
p.
1205.
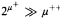 .
.