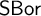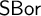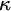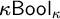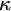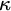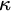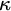1 Introduction
A standard Borel space is a measurable space (i.e., set equipped with
![]() $\sigma $
-algebra of subsets) which is isomorphic to a Borel subspace of Cantor space
$\sigma $
-algebra of subsets) which is isomorphic to a Borel subspace of Cantor space
![]() $2^{\mathbb {N}}$
. Standard Borel spaces and Borel maps (i.e., preimages of Borel sets are Borel) are ubiquitous in descriptive set theory as a basic model of “definable sets” and “definable functions” between them (see [Reference Kechris18]). The notion of “definability” here is a coarse one where, roughly speaking, all countable information is considered definable. As a result, standard Borel spaces are closed under familiar set operations of countable arity, e.g., countable products, countable unions, and injective Borel images.
$2^{\mathbb {N}}$
. Standard Borel spaces and Borel maps (i.e., preimages of Borel sets are Borel) are ubiquitous in descriptive set theory as a basic model of “definable sets” and “definable functions” between them (see [Reference Kechris18]). The notion of “definability” here is a coarse one where, roughly speaking, all countable information is considered definable. As a result, standard Borel spaces are closed under familiar set operations of countable arity, e.g., countable products, countable unions, and injective Borel images.
In this paper, we give a purely “synthetic” characterization of the category
![]() $\mathsf {SBor}$
of standard Borel spaces and Borel maps: we prove that
$\mathsf {SBor}$
of standard Borel spaces and Borel maps: we prove that
![]() $\mathsf {SBor}$
is the free category generated by some familiar set operations (e.g., those above) subject to some obvious compatibility conditions between them (e.g., products distribute over unions). In other words, every standard Borel space or Borel map can be regarded as a formal expression built from these operations (e.g.,
$\mathsf {SBor}$
is the free category generated by some familiar set operations (e.g., those above) subject to some obvious compatibility conditions between them (e.g., products distribute over unions). In other words, every standard Borel space or Borel map can be regarded as a formal expression built from these operations (e.g.,
![]() $\bigsqcup\nolimits _{n \le \aleph _0} 2^n$
), and more significantly, every true statement about the spaces or maps denoted by such expressions (e.g., a given map is an isomorphism) can be deduced in a purely formal manner from the compatibility conditions.
$\bigsqcup\nolimits _{n \le \aleph _0} 2^n$
), and more significantly, every true statement about the spaces or maps denoted by such expressions (e.g., a given map is an isomorphism) can be deduced in a purely formal manner from the compatibility conditions.
The operations on
![]() $\mathsf {SBor}$
take the form of certain well-behaved limits and colimits, which we now briefly describe (see Section 2 for the precise definitions). Recall that limits in a category
$\mathsf {SBor}$
take the form of certain well-behaved limits and colimits, which we now briefly describe (see Section 2 for the precise definitions). Recall that limits in a category
![]() $\mathsf {C}$
give abstract versions of such set operations as products (including nullary, i.e., the 1-element set), preimages of subsets, inverse limits, and the equality binary relation. Limits that exist in
$\mathsf {C}$
give abstract versions of such set operations as products (including nullary, i.e., the 1-element set), preimages of subsets, inverse limits, and the equality binary relation. Limits that exist in
![]() $\mathsf {C}$
are automatically “fully compatible” with themselves.Footnote
1
We call
$\mathsf {C}$
are automatically “fully compatible” with themselves.Footnote
1
We call
![]() $\mathsf {C}$
complete, or more generally
$\mathsf {C}$
complete, or more generally
![]() $\kappa $
-complete for a regular cardinal
$\kappa $
-complete for a regular cardinal
![]() $\kappa $
, if
$\kappa $
, if
![]() $\mathsf {C}$
has all (
$\mathsf {C}$
has all (
![]() $\kappa $
-ary) limits. Colimits, dual to limits, are abstract versions of such set operations as disjoint unions (given by coproducts), images, and quotients. There are many well-studied compatibility conditions between limits and colimits, often known as “exactness conditions,” based on conditions that hold in familiar categories such as
$\kappa $
-ary) limits. Colimits, dual to limits, are abstract versions of such set operations as disjoint unions (given by coproducts), images, and quotients. There are many well-studied compatibility conditions between limits and colimits, often known as “exactness conditions,” based on conditions that hold in familiar categories such as
![]() $\mathsf {Set}$
(see, e.g., [Reference Garner and Lack11]). For a category
$\mathsf {Set}$
(see, e.g., [Reference Garner and Lack11]). For a category
![]() $\mathsf {C}$
with finite limits and coproducts, the condition known as extensivity [Reference Carboni, Lack and Walters5], based on the behavior of disjoint unions in
$\mathsf {C}$
with finite limits and coproducts, the condition known as extensivity [Reference Carboni, Lack and Walters5], based on the behavior of disjoint unions in
![]() $\mathsf {Set}$
, says that a map
$\mathsf {Set}$
, says that a map
![]() $Y \to \bigsqcup\nolimits _{i \in I} X_i \in \mathsf {C}$
into a finite coproduct is the same thing as a partition
$Y \to \bigsqcup\nolimits _{i \in I} X_i \in \mathsf {C}$
into a finite coproduct is the same thing as a partition
![]() $Y = \bigsqcup\nolimits _{i \in I} Y_i$
together with maps
$Y = \bigsqcup\nolimits _{i \in I} Y_i$
together with maps
![]() $Y_i \to X_i$
for each i. More generally,
$Y_i \to X_i$
for each i. More generally,
![]() $\mathsf {C}$
is
$\mathsf {C}$
is
![]() $\kappa $
-extensive if it has
$\kappa $
-extensive if it has
![]() $\kappa $
-ary coproducts obeying the analogous condition. Finally, we say that an extensive category
$\kappa $
-ary coproducts obeying the analogous condition. Finally, we say that an extensive category
![]() $\mathsf {C}$
is Boolean if the subobject poset
$\mathsf {C}$
is Boolean if the subobject poset
![]() $\mathrm {Sub}_{\mathsf {C}}(X)$
of each object
$\mathrm {Sub}_{\mathsf {C}}(X)$
of each object
![]() $X \in \mathsf {C}$
is a Boolean algebra.
$X \in \mathsf {C}$
is a Boolean algebra.
Theorem 1.1. The category
![]() $\mathsf {SBor}$
of standard Borel spaces and Borel maps is the initial object in the 2-category of countably complete Boolean (countably) extensive categories.
$\mathsf {SBor}$
of standard Borel spaces and Borel maps is the initial object in the 2-category of countably complete Boolean (countably) extensive categories.
Here, the morphisms
![]() $\mathcal {F} : \mathsf {C} \to \mathsf {D}$
between two countably complete Boolean countably extensive categories are the functors preserving all of these operations, i.e., the countably continuous, countably extensive functors. As with most freeness statements about categories equipped with algebraic operations, we necessarily must consider the 2-category of countably complete Boolean countably extensive categories, countably continuous countably extensive functors between them, and natural transformations between such functors. This is because algebraic operations on a category (e.g., limits) are almost never uniquely defined, but only defined up to canonical isomorphism; thus, the usual universal property of a free algebra must be weakened to take natural isomorphisms between functors into account. Accordingly, the notion of initial object in Theorem 1.1 refers to what is known as a bicolimit in 2-category theory (see [Reference Blackwell, Kelly and Power2]): for any other countably complete Boolean countably extensive category
$\mathcal {F} : \mathsf {C} \to \mathsf {D}$
between two countably complete Boolean countably extensive categories are the functors preserving all of these operations, i.e., the countably continuous, countably extensive functors. As with most freeness statements about categories equipped with algebraic operations, we necessarily must consider the 2-category of countably complete Boolean countably extensive categories, countably continuous countably extensive functors between them, and natural transformations between such functors. This is because algebraic operations on a category (e.g., limits) are almost never uniquely defined, but only defined up to canonical isomorphism; thus, the usual universal property of a free algebra must be weakened to take natural isomorphisms between functors into account. Accordingly, the notion of initial object in Theorem 1.1 refers to what is known as a bicolimit in 2-category theory (see [Reference Blackwell, Kelly and Power2]): for any other countably complete Boolean countably extensive category
![]() $\mathsf {C}$
, the category of countably continuous countably extensive functors
$\mathsf {C}$
, the category of countably continuous countably extensive functors
![]() $\mathsf {SBor} \to \mathsf {C}$
is (not necessarily isomorphic but) equivalent to the one-object one-morphism category. In particular, there is a unique such functor
$\mathsf {SBor} \to \mathsf {C}$
is (not necessarily isomorphic but) equivalent to the one-object one-morphism category. In particular, there is a unique such functor
![]() $\mathsf {SBor} \to \mathsf {C}$
, up to unique natural isomorphism between any two such functors. Note that this characterizes
$\mathsf {SBor} \to \mathsf {C}$
, up to unique natural isomorphism between any two such functors. Note that this characterizes
![]() $\mathsf {SBor}$
up to equivalence.
$\mathsf {SBor}$
up to equivalence.
The parenthetical in Theorem 1.1 is because countable limits, finite extensivity, and Booleanness easily imply countable extensivity (see Lemma 2.5).
We would like to stress that Theorem 1.1 characterizes
![]() $\mathsf {SBor}$
as an abstract category, i.e., without an a priori given underlying set functor
$\mathsf {SBor}$
as an abstract category, i.e., without an a priori given underlying set functor
![]() $\mathsf {SBor} \to \mathsf {Set}$
. Based on the inductive definition of Borel sets, it is fairly obvious that
$\mathsf {SBor} \to \mathsf {Set}$
. Based on the inductive definition of Borel sets, it is fairly obvious that
![]() $\mathsf {SBor}$
as a (conservative) subcategory of
$\mathsf {SBor}$
as a (conservative) subcategory of
![]() $\mathsf {Set}$
is generated by the specified operations.Footnote
2
Thus, the force of Theorem 1.1 is that any true statement in
$\mathsf {Set}$
is generated by the specified operations.Footnote
2
Thus, the force of Theorem 1.1 is that any true statement in
![]() $\mathsf {SBor}$
only mentioning these operations may be deduced purely formally from the compatibility axioms.
$\mathsf {SBor}$
only mentioning these operations may be deduced purely formally from the compatibility axioms.
There is a classical result much along the lines of Theorem 1.1, and forming an important part of its proof: the Loomis–Sikorski representation theorem says (in one equivalent formulation) that the Borel
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {B}(2^{\mathbb {N}})$
of Cantor space is freely generated, as an abstract Boolean
$\mathcal {B}(2^{\mathbb {N}})$
of Cantor space is freely generated, as an abstract Boolean
![]() $\sigma $
-algebra (countably complete Boolean algebra), by the subbasic clopen sets in
$\sigma $
-algebra (countably complete Boolean algebra), by the subbasic clopen sets in
![]() $2^{\mathbb {N}}$
(see Section 4). An easy consequence is that we have a dual equivalence of categories
$2^{\mathbb {N}}$
(see Section 4). An easy consequence is that we have a dual equivalence of categories
 $$ \begin{align*} \mathsf{SBor} &\cong \sigma\mathsf{Bool}_{\sigma}^{\mathrm{op}} \\ X &\mapsto \mathcal{B}(X) \\ (f : X \to Y) &\mapsto (f^{-1} : \mathcal{B}(Y) \to \mathcal{B}(X)) \end{align*} $$
$$ \begin{align*} \mathsf{SBor} &\cong \sigma\mathsf{Bool}_{\sigma}^{\mathrm{op}} \\ X &\mapsto \mathcal{B}(X) \\ (f : X \to Y) &\mapsto (f^{-1} : \mathcal{B}(Y) \to \mathcal{B}(X)) \end{align*} $$
with the category
![]() $\sigma \mathsf {Bool}_{\sigma }$
of countably presented Boolean
$\sigma \mathsf {Bool}_{\sigma }$
of countably presented Boolean
![]() $\sigma $
-algebras. In fact, this equivalence, which we will refer to as Loomis–Sikorski duality, is the only role of classical descriptive set theory in Theorem 1.1, which is a consequence of Loomis–Sikorski duality together with
$\sigma $
-algebras. In fact, this equivalence, which we will refer to as Loomis–Sikorski duality, is the only role of classical descriptive set theory in Theorem 1.1, which is a consequence of Loomis–Sikorski duality together with
Theorem 1.2 (Theorem 5.9)
For any infinite regular cardinal
![]() $\kappa $
, the dual
$\kappa $
, the dual
![]() $\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
of the category
$\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
of the category
![]() $\kappa \mathsf {Bool}_{\kappa }$
of
$\kappa \mathsf {Bool}_{\kappa }$
of
![]() $\kappa $
-presented
$\kappa $
-presented
![]() $\kappa $
-complete Boolean algebras is the initial object in the 2-category of
$\kappa $
-complete Boolean algebras is the initial object in the 2-category of
![]() $\kappa $
-complete Boolean (
$\kappa $
-complete Boolean (
![]() $\kappa $
-)extensive categories.
$\kappa $
-)extensive categories.
When
![]() $\kappa = \omega _1$
, this reduces to Theorem 1.1 by Loomis–Sikorski duality. Also note that when
$\kappa = \omega _1$
, this reduces to Theorem 1.1 by Loomis–Sikorski duality. Also note that when
![]() $\kappa = \omega $
, we recover the well-known fact that the category of finite sets (dual to
$\kappa = \omega $
, we recover the well-known fact that the category of finite sets (dual to
![]() $\omega \mathsf {Bool}_{\omega }$
, the category of finite Boolean algebras) is the initial finitely complete extensive category (see, e.g., [Reference Johnstone17, Corollary A1.4.7]).
$\omega \mathsf {Bool}_{\omega }$
, the category of finite Boolean algebras) is the initial finitely complete extensive category (see, e.g., [Reference Johnstone17, Corollary A1.4.7]).
We now briefly discuss the proof of Theorem 1.2. By the Lusin–Suslin theorem [Reference Kechris18, Theorem 15.1], Borel injections between standard Borel spaces have Borel images, whence subobjects in
![]() $\mathsf {SBor}$
are Borel subspaces; analogously, by a result of Lagrange [Reference Lagrange19] (see Corollary 3.4), subobjects of
$\mathsf {SBor}$
are Borel subspaces; analogously, by a result of Lagrange [Reference Lagrange19] (see Corollary 3.4), subobjects of
![]() $A \in \kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
are in canonical bijection with elements
$A \in \kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
are in canonical bijection with elements
![]() $a \in A$
. Thus, in order to exploit the universal property of
$a \in A$
. Thus, in order to exploit the universal property of
![]() $\kappa $
-presented algebras in the proof of Theorem 1.2, it is convenient to reformulate the notion of
$\kappa $
-presented algebras in the proof of Theorem 1.2, it is convenient to reformulate the notion of
![]() $\kappa $
-complete Boolean
$\kappa $
-complete Boolean
![]() $\kappa $
-extensive category in terms of “objects and subobjects” instead of “objects and morphisms.” This is achieved by the standard notion of hyperdoctrine from categorical logic, due to Lawvere [Reference Lawvere20]. For a category
$\kappa $
-extensive category in terms of “objects and subobjects” instead of “objects and morphisms.” This is achieved by the standard notion of hyperdoctrine from categorical logic, due to Lawvere [Reference Lawvere20]. For a category
![]() $\mathsf {C}$
with enough compatible limits and colimits, we may equivalently describe
$\mathsf {C}$
with enough compatible limits and colimits, we may equivalently describe
![]() $\mathsf {C}$
as a collection of objects together with, for each tuple
$\mathsf {C}$
as a collection of objects together with, for each tuple
![]() $\vec {A}$
of objects in
$\vec {A}$
of objects in
![]() $\mathsf {C}$
, a lattice
$\mathsf {C}$
, a lattice
![]() $\mathrm {Sub}_{\mathsf {C}}(\vec {A})$
of “
$\mathrm {Sub}_{\mathsf {C}}(\vec {A})$
of “
![]() $\vec {A}$
-ary predicates,” thought of as the subobject lattice of
$\vec {A}$
-ary predicates,” thought of as the subobject lattice of
![]() $\prod \vec {A}$
, equipped with “variable substitution” and “quantification” maps between them as well as distinguished “equality predicates”
$\prod \vec {A}$
, equipped with “variable substitution” and “quantification” maps between them as well as distinguished “equality predicates”
![]() $({=_A}) \in \mathrm {Sub}_{\mathsf {C}}(A, A)$
for each A. From these data, called the subobject hyperdoctrine of
$({=_A}) \in \mathrm {Sub}_{\mathsf {C}}(A, A)$
for each A. From these data, called the subobject hyperdoctrine of
![]() $\mathsf {C}$
,
$\mathsf {C}$
,
![]() $\mathsf {C}$
may be reconstructed by taking morphisms to be binary predicates which are “function graphs” (expressed internally). See [Reference Jacobs14, Reference Lawvere20] for details.
$\mathsf {C}$
may be reconstructed by taking morphisms to be binary predicates which are “function graphs” (expressed internally). See [Reference Jacobs14, Reference Lawvere20] for details.
Rather than work directly with hyperdoctrines, we prefer to work with their presentations, i.e., first-order theories. Given a multi-sorted relational first-order theory
![]() $\mathcal {T}$
in a language
$\mathcal {T}$
in a language
![]() $\mathcal {L}$
, a hyperdoctrine may be constructed whose objects are the sorts and whose predicates are the
$\mathcal {L}$
, a hyperdoctrine may be constructed whose objects are the sorts and whose predicates are the
![]() $\mathcal {T}$
-provable equivalence classes of formulas. Constructing a category from this hyperdoctrine as above yields the syntactic category
$\mathcal {T}$
-provable equivalence classes of formulas. Constructing a category from this hyperdoctrine as above yields the syntactic category
![]() ${\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle }$
of the theory
${\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle }$
of the theory
![]() $\mathcal {T}$
, which is the category “presented” by
$\mathcal {T}$
, which is the category “presented” by
![]() $(\mathcal {L}, \mathcal {T})$
in terms of objects (the sorts), subobjects (relation symbols in
$(\mathcal {L}, \mathcal {T})$
in terms of objects (the sorts), subobjects (relation symbols in
![]() $\mathcal {L}$
), and relations between subobjects (axioms of
$\mathcal {L}$
), and relations between subobjects (axioms of
![]() $\mathcal {T}$
) (see [Reference Makkai and Reyes23, Chapter 8], [Reference Johnstone17, Section D1.3]). We will give in Section 5 in some detail the one-step construction (bypassing hyperdoctrines) of syntactic categories for theories presenting
$\mathcal {T}$
) (see [Reference Makkai and Reyes23, Chapter 8], [Reference Johnstone17, Section D1.3]). We will give in Section 5 in some detail the one-step construction (bypassing hyperdoctrines) of syntactic categories for theories presenting
![]() $\kappa $
-complete Boolean
$\kappa $
-complete Boolean
![]() $\kappa $
-extensive categories. One reason for our level of detail is that the fragment of first-order logic whose theories present such categories does not appear to have been well-studied, and involves some technical complications: the fragment consists of formulas in the
$\kappa $
-extensive categories. One reason for our level of detail is that the fragment of first-order logic whose theories present such categories does not appear to have been well-studied, and involves some technical complications: the fragment consists of formulas in the
![]() $\kappa $
-ary infinitary first-order logic
$\kappa $
-ary infinitary first-order logic
![]() $\mathcal {L}_{\kappa \kappa }$
(with
$\mathcal {L}_{\kappa \kappa }$
(with
![]() $\kappa $
-ary quantifiers and
$\kappa $
-ary quantifiers and
![]() $\bigwedge , \bigvee $
) which are “almost quantifier-free” in that
$\bigwedge , \bigvee $
) which are “almost quantifier-free” in that
![]() $\forall $
does not appear, and every
$\forall $
does not appear, and every
![]() $\exists $
that appears is already provably unique modulo the theory. (This “provably unique
$\exists $
that appears is already provably unique modulo the theory. (This “provably unique
![]() $\exists $
” is familiar in categorical logic from finite-limit logic or Cartesian logic, the fragment of
$\exists $
” is familiar in categorical logic from finite-limit logic or Cartesian logic, the fragment of
![]() $\mathcal {L}_{\omega \omega }$
used to present finitely complete categories; see [Reference Johnstone17, Definition D1.3.4].)
$\mathcal {L}_{\omega \omega }$
used to present finitely complete categories; see [Reference Johnstone17, Definition D1.3.4].)
The method of proof of Theorem 1.2 will be to show that
![]() $\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
is presented by a “trivial” theory axiomatizing structure automatically present in every
$\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
is presented by a “trivial” theory axiomatizing structure automatically present in every
![]() $\kappa $
-complete Boolean
$\kappa $
-complete Boolean
![]() $\kappa $
-extensive category. That is, we show that
$\kappa $
-extensive category. That is, we show that
![]() $\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
is equivalent to the syntactic category of such a theory. This will be easy for the part of the syntactic category consisting of quantifier-free formulas. So the main difficulty will be to show that the “provably unique
$\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
is equivalent to the syntactic category of such a theory. This will be easy for the part of the syntactic category consisting of quantifier-free formulas. So the main difficulty will be to show that the “provably unique
![]() $\exists $
” quantifier can be provably eliminated from formulas. In terms of
$\exists $
” quantifier can be provably eliminated from formulas. In terms of
![]() $\mathsf {SBor}$
, this amounts to showing that an injective Borel image can be “algebraically witnessed”; thus the key to the proof will be an analysis of the algebraic content of the proof of the Lusin–Suslin theorem and its
$\mathsf {SBor}$
, this amounts to showing that an injective Borel image can be “algebraically witnessed”; thus the key to the proof will be an analysis of the algebraic content of the proof of the Lusin–Suslin theorem and its
![]() $\kappa $
-ary analog (see Remark 3.6 and Lemma 5.8).
$\kappa $
-ary analog (see Remark 3.6 and Lemma 5.8).
1.1 Connections with other work
Abstract characterizations of various categories of topological spaces are known. It is folklore that the category of Stone spaces is the pro-completion of the category of finite sets (see [Reference Johnstone16, Ch. VI Theorem 2.3]). In [Reference Marra and Reggio24], a characterization is given of the category of compact Hausdorff spaces.
Recently, there have been efforts to formulate a synthetic descriptive set theory (see [Reference Pauly and de Brecht25]). The goal of such a program is to uniformly recover key notions and results from several known versions of descriptive set theory (classical, effective, and generalized to other kinds of spaces, e.g., [Reference Selivanov26]) in an abstract manner from the relevant categories of spaces, thereby providing an explanation for the informal analogies between these theories. Theorem 1.1 shows that in the boldface, purely Borel context (without any topology), we have a complete answer as to how much categorical structure and axioms are required to fully recover the classical theory in the form of
![]() $\mathsf {SBor}$
. Moreover, the recovery here takes the satisfying form of a universal property uniquely characterizing
$\mathsf {SBor}$
. Moreover, the recovery here takes the satisfying form of a universal property uniquely characterizing
![]() $\mathsf {SBor}$
among all possible “models” of these axioms.
$\mathsf {SBor}$
among all possible “models” of these axioms.
The Loomis–Sikorski duality
![]() $\mathsf {SBor} \cong \sigma \mathsf {Bool}_{\sigma }^{\mathrm {op}}$
is part of a family of analogies (see [Reference Chen9, Reference Heckmann12, Reference Isbell13], [Reference Chen7, arXiv version]) between descriptive set theory and pointless topology or locale theory (see [Reference Johnstone16], [Reference Johnstone17, Sections C1.1–2]) suggesting that elementary classical descriptive set theory is in many ways the “countably presented fragment” of locale theory. Adopting this point of view, one can define a standard
$\mathsf {SBor} \cong \sigma \mathsf {Bool}_{\sigma }^{\mathrm {op}}$
is part of a family of analogies (see [Reference Chen9, Reference Heckmann12, Reference Isbell13], [Reference Chen7, arXiv version]) between descriptive set theory and pointless topology or locale theory (see [Reference Johnstone16], [Reference Johnstone17, Sections C1.1–2]) suggesting that elementary classical descriptive set theory is in many ways the “countably presented fragment” of locale theory. Adopting this point of view, one can define a standard
![]() $\kappa $
-Borel locale X to formally mean the same thing as a
$\kappa $
-Borel locale X to formally mean the same thing as a
![]() $\kappa $
-presented
$\kappa $
-presented
![]() $\kappa $
-complete Boolean algebra
$\kappa $
-complete Boolean algebra
![]() $\mathcal {B}_{\kappa }(X)$
; a
$\mathcal {B}_{\kappa }(X)$
; a
![]() $\kappa $
-Borel map
$\kappa $
-Borel map
![]() $f : X \to Y$
between such
$f : X \to Y$
between such
![]() $X, Y$
is a
$X, Y$
is a
![]() $\kappa $
-Boolean homomorphism
$\kappa $
-Boolean homomorphism
![]() $f^* : \mathcal {B}_{\kappa }(Y) \to \mathcal {B}_{\kappa }(X)$
. Thus, standard
$f^* : \mathcal {B}_{\kappa }(Y) \to \mathcal {B}_{\kappa }(X)$
. Thus, standard
![]() $\kappa $
-Borel locales are to standard Borel spaces as
$\kappa $
-Borel locales are to standard Borel spaces as
![]() $\kappa $
-copresented
$\kappa $
-copresented
![]() $\kappa $
-locales (see [Reference Madden22]) are to de Brecht’s quasi-Polish spaces (see [Reference de Brecht4. Reference Heckmann12]). Theorem 1.2 then becomes the literal
$\kappa $
-locales (see [Reference Madden22]) are to de Brecht’s quasi-Polish spaces (see [Reference de Brecht4. Reference Heckmann12]). Theorem 1.2 then becomes the literal
![]() $\kappa $
-ary generalization of Theorem 1.1. The proof of Theorem 1.2 is largely informed by this point of view as well, e.g., to show that
$\kappa $
-ary generalization of Theorem 1.1. The proof of Theorem 1.2 is largely informed by this point of view as well, e.g., to show that
![]() $\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
is indeed
$\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
is indeed
![]() $\kappa $
-complete
$\kappa $
-complete
![]() $\kappa $
-extensive (see Propositions 3.7 and 3.8), or the aforementioned result of Lagrange [Reference Lagrange19] which is a
$\kappa $
-extensive (see Propositions 3.7 and 3.8), or the aforementioned result of Lagrange [Reference Lagrange19] which is a
![]() $\kappa $
-ary version of the Lusin separation theorem playing an analogous role in the proof of
$\kappa $
-ary version of the Lusin separation theorem playing an analogous role in the proof of
![]() $\kappa $
-ary Lusin–Suslin (see Remark 3.6). See [Reference Chen8] for a systematic development of these ideas. To keep this paper as concrete as possible, we will not explicitly refer to standard
$\kappa $
-ary Lusin–Suslin (see Remark 3.6). See [Reference Chen8] for a systematic development of these ideas. To keep this paper as concrete as possible, we will not explicitly refer to standard
![]() $\kappa $
-Borel locales in what follows.
$\kappa $
-Borel locales in what follows.
1.2 Contents of paper
This paper should hopefully be readable with basic category-theoretic background, although some familiarity with categorical logic would be helpful.
In Section 2, we review some (2-)category theory, including extensive categories and variants.
In Section 3, we review and introduce needed background on
![]() $\kappa $
-Boolean algebras, including the results of Lagrange [Reference Lagrange19] as well as the fact that
$\kappa $
-Boolean algebras, including the results of Lagrange [Reference Lagrange19] as well as the fact that
![]() $\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
is
$\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
is
![]() $\kappa $
-complete Boolean
$\kappa $
-complete Boolean
![]() $\kappa $
-extensive.
$\kappa $
-extensive.
In Section 4, we review Loomis–Sikorski duality, which we formulate in terms of a Stone-type dual adjunction (in the sense of, e.g., [Reference Johnstone16, VI Section 4]) between measurable spaces and Boolean
![]() $\sigma $
-algebras. We include a self-contained proof.
$\sigma $
-algebras. We include a self-contained proof.
Finally, in Section 5, we develop the “almost quantifier-free” fragment of
![]() $\mathcal {L}_{\kappa \kappa }$
, and show that its theories present (via the syntactic category construction)
$\mathcal {L}_{\kappa \kappa }$
, and show that its theories present (via the syntactic category construction)
![]() $\kappa $
-complete Boolean
$\kappa $
-complete Boolean
![]() $\kappa $
-(sub)extensive categories, and use such a theory to prove Theorem 1.2.
$\kappa $
-(sub)extensive categories, and use such a theory to prove Theorem 1.2.
2 Categories
We assume familiarity with basic notions of category theory, including, e.g., limits, colimits, and adjoint functors (see, e.g., [Reference Borceux3, Reference Mac Lane21]). Categories will be denoted with sans-serif symbols like
![]() $\mathsf {C}$
. Hom-sets will be denoted
$\mathsf {C}$
. Hom-sets will be denoted
![]() $\mathsf {C}(X, Y)$
for
$\mathsf {C}(X, Y)$
for
![]() $X, Y \in \mathsf {C}$
; identity morphisms will be denoted
$X, Y \in \mathsf {C}$
; identity morphisms will be denoted
![]() $1_X : X \to X$
. The category of sets will be denoted
$1_X : X \to X$
. The category of sets will be denoted
![]() $\mathsf {Set}$
. The terminal category has a single object and single (identity) morphism.
$\mathsf {Set}$
. The terminal category has a single object and single (identity) morphism.
Fix throughout the paper an infinite regular cardinal
![]() $\kappa $
; the case
$\kappa $
; the case
![]() $\kappa = \omega _1$
will be typical. By
$\kappa = \omega _1$
will be typical. By
![]() $\kappa $
-ary, we mean of size
$\kappa $
-ary, we mean of size
![]() ${<}\kappa $
. Let
${<}\kappa $
. Let
![]() $\mathsf {Set}_{\kappa } \subseteq \mathsf {Set}$
be the full subcategory of
$\mathsf {Set}_{\kappa } \subseteq \mathsf {Set}$
be the full subcategory of
![]() $\kappa $
-ary sets. Also fix some set
$\kappa $
-ary sets. Also fix some set
![]() $\mathbb {U}$
of size
$\mathbb {U}$
of size
![]() ${\ge} \kappa $
(e.g.,
${\ge} \kappa $
(e.g.,
![]() $\mathbb {U} := \kappa $
), for convenience assuming
$\mathbb {U} := \kappa $
), for convenience assuming
![]() $\mathbb {N} \subseteq \mathbb {U}$
, and let
$\mathbb {N} \subseteq \mathbb {U}$
, and let
![]() $\mathsf {Set}^{\prime }_{\kappa } \subseteq \mathsf {Set}_{\kappa }$
be the full subcategory of
$\mathsf {Set}^{\prime }_{\kappa } \subseteq \mathsf {Set}_{\kappa }$
be the full subcategory of
![]() $\kappa $
-ary subsets of
$\kappa $
-ary subsets of
![]() $\mathbb {U}$
; thus
$\mathbb {U}$
; thus
![]() $\mathsf {Set}^{\prime }_{\kappa } \subseteq \mathsf {Set}_{\kappa }$
is a small full subcategory containing a set of each cardinality
$\mathsf {Set}^{\prime }_{\kappa } \subseteq \mathsf {Set}_{\kappa }$
is a small full subcategory containing a set of each cardinality
![]() ${<}\kappa $
, hence equivalent to
${<}\kappa $
, hence equivalent to
![]() $\mathsf {Set}_{\kappa }$
.
$\mathsf {Set}_{\kappa }$
.
Recall that a subobject of an object
![]() $X \in \mathsf {C}$
of a category
$X \in \mathsf {C}$
of a category
![]() $\mathsf {C}$
is an equivalence class of monomorphisms
$\mathsf {C}$
is an equivalence class of monomorphisms
![]() $f : A \hookrightarrow X \in \mathsf {C}$
with respect to the preorder
$f : A \hookrightarrow X \in \mathsf {C}$
with respect to the preorder
(such an h is necessarily unique). As is common, we will often abuse terminology regarding subobjects: we also refer to single monomorphisms as subobjects, identified with their equivalence classes; we sometimes write a subobject
![]() $f : A \hookrightarrow X$
(i.e., its equivalence class) simply as
$f : A \hookrightarrow X$
(i.e., its equivalence class) simply as
![]() $A \subseteq X$
; and we generally use familiar notations for subsets with the obvious meanings (e.g.,
$A \subseteq X$
; and we generally use familiar notations for subsets with the obvious meanings (e.g.,
![]() $\cup , \cap $
). Let
$\cup , \cap $
). Let
partially ordered by (the partial order induced on equivalence classes by)
![]() $\subseteq $
.
$\subseteq $
.
A category
![]() $\mathsf {C}$
is
$\mathsf {C}$
is
![]() $\kappa $
-complete if it has all
$\kappa $
-complete if it has all
![]() $\kappa $
-ary limits; a functor
$\kappa $
-ary limits; a functor
![]() $\mathcal {F} : \mathsf {C} \to \mathsf {D}$
between two
$\mathcal {F} : \mathsf {C} \to \mathsf {D}$
between two
![]() $\kappa $
-complete categories is
$\kappa $
-complete categories is
![]() $\kappa $
-continuous if it preserves all
$\kappa $
-continuous if it preserves all
![]() $\kappa $
-ary limits. In a
$\kappa $
-ary limits. In a
![]() $\kappa $
-complete category, each subobject poset
$\kappa $
-complete category, each subobject poset
![]() $\mathrm {Sub}(X)$
has
$\mathrm {Sub}(X)$
has
![]() $\kappa $
-ary meets given by (wide) pullback; we denote meets of
$\kappa $
-ary meets given by (wide) pullback; we denote meets of
![]() $A_i \subseteq X$
by either
$A_i \subseteq X$
by either
![]() $\bigcap _i A_i$
, or
$\bigcap _i A_i$
, or
![]() $\bigwedge\nolimits _i A_i$
, or (as pullbacks)
$\bigwedge\nolimits _i A_i$
, or (as pullbacks)
![]() $\prod _X (A_i)_i$
. For each
$\prod _X (A_i)_i$
. For each
![]() $f : X \to Y$
, the pullback map
$f : X \to Y$
, the pullback map
between subobject posets preserves
![]() $\kappa $
-ary meets; we thus get a functor
$\kappa $
-ary meets; we thus get a functor
to the category
![]() $\mathsf {\kappa {\bigwedge }Lat}$
of
$\mathsf {\kappa {\bigwedge }Lat}$
of
![]() $\kappa $
-complete meet semilattices. A
$\kappa $
-complete meet semilattices. A
![]() $\kappa $
-continuous functor
$\kappa $
-continuous functor
![]() $\mathcal {F} : \mathsf {C} \to \mathsf {D}$
between
$\mathcal {F} : \mathsf {C} \to \mathsf {D}$
between
![]() $\kappa $
-complete categories preserves monomorphisms, and hence induces a map between subobject posets
$\kappa $
-complete categories preserves monomorphisms, and hence induces a map between subobject posets
for each
![]() $X \in \mathsf {C}$
, which also preserves
$X \in \mathsf {C}$
, which also preserves
![]() $\kappa $
-ary meets.
$\kappa $
-ary meets.
A finitely complete category
![]() $\mathsf {C}$
is extensive (see [Reference Carboni, Lack and Walters5]) if it has finite coproducts which are pullback-stable and disjoint, defined as follows. A coproduct
$\mathsf {C}$
is extensive (see [Reference Carboni, Lack and Walters5]) if it has finite coproducts which are pullback-stable and disjoint, defined as follows. A coproduct
![]() $\bigsqcup\nolimits _{i \in I} X_i$
of objects
$\bigsqcup\nolimits _{i \in I} X_i$
of objects
![]() $X_i \in \mathsf {C}$
with cocone
$X_i \in \mathsf {C}$
with cocone
![]() $(\iota _i : X_i \to \bigsqcup\nolimits _{i \in I} X_i)_{i \in I}$
is pullback-stable if for any morphism
$(\iota _i : X_i \to \bigsqcup\nolimits _{i \in I} X_i)_{i \in I}$
is pullback-stable if for any morphism
![]() $f : Y \to \bigsqcup\nolimits _{i \in I} X_i \in \mathsf {C}$
, the pullbacks
$f : Y \to \bigsqcup\nolimits _{i \in I} X_i \in \mathsf {C}$
, the pullbacks
![]() $f^*(\iota _i) : f^*(X_i) \to Y$
of the morphisms
$f^*(\iota _i) : f^*(X_i) \to Y$
of the morphisms
![]() $\iota _i$
along f, as in the diagram
$\iota _i$
along f, as in the diagram

together form a cocone which exhibits Y as the coproduct
![]() $\bigsqcup\nolimits _i f^*(X_i)$
. In particular, when
$\bigsqcup\nolimits _i f^*(X_i)$
. In particular, when
![]() $I = \emptyset $
, this means we have an initial object
$I = \emptyset $
, this means we have an initial object
![]() $0 \in \mathsf {C}$
which is strict, meaning any
$0 \in \mathsf {C}$
which is strict, meaning any
![]() $f : Y \to 0$
is an isomorphism. A coproduct
$f : Y \to 0$
is an isomorphism. A coproduct
![]() $\bigsqcup\nolimits _i X_i$
is disjoint if each of the cocone morphisms
$\bigsqcup\nolimits _i X_i$
is disjoint if each of the cocone morphisms
![]() $\iota _i : X_i \to \bigsqcup\nolimits _{i \in I} X_i$
is monic, and for any
$\iota _i : X_i \to \bigsqcup\nolimits _{i \in I} X_i$
is monic, and for any
![]() $i \ne j$
, the pullback of
$i \ne j$
, the pullback of
![]() $\iota _i, \iota _j$
is the initial object. For extensivity, it is enough to consider nullary and binary coproducts, i.e., for there to be a strict initial object, as well as pullback-stable and disjoint binary coproducts. More generally, we say that
$\iota _i, \iota _j$
is the initial object. For extensivity, it is enough to consider nullary and binary coproducts, i.e., for there to be a strict initial object, as well as pullback-stable and disjoint binary coproducts. More generally, we say that
![]() $\mathsf {C}$
is
$\mathsf {C}$
is
![]() $\kappa $
-extensive if it has pullback-stable and disjoint
$\kappa $
-extensive if it has pullback-stable and disjoint
![]() $\kappa $
-ary coproducts (disjointness needs only be checked for binary coproducts). A finitely continuous functor
$\kappa $
-ary coproducts (disjointness needs only be checked for binary coproducts). A finitely continuous functor
![]() $\mathcal {F} : \mathsf {C} \to \mathsf {D}$
between finitely complete (
$\mathcal {F} : \mathsf {C} \to \mathsf {D}$
between finitely complete (
![]() $\kappa $
-)extensive categories is (
$\kappa $
-)extensive categories is (
![]() $\kappa $
-)extensive if it preserves finite (resp.
$\kappa $
-)extensive if it preserves finite (resp.
![]() $\kappa $
-ary) coproducts.
$\kappa $
-ary) coproducts.
A finitely complete category
![]() $\mathsf {C}$
is subextensive if it has a strict initial object
$\mathsf {C}$
is subextensive if it has a strict initial object
![]() $0$
, which implies that every subobject poset
$0$
, which implies that every subobject poset
![]() $\mathrm {Sub}(X)$
has a least element
$\mathrm {Sub}(X)$
has a least element
![]() $0 \hookrightarrow X$
, and any two subobjects
$0 \hookrightarrow X$
, and any two subobjects
![]() $A, B \subseteq X$
which are disjoint (meaning their meet is
$A, B \subseteq X$
which are disjoint (meaning their meet is
![]() $0$
) have a pullback-stable join in
$0$
) have a pullback-stable join in
![]() $\mathrm {Sub}(X)$
. (This notion is part of the definition of coherent category [see, e.g., [Reference Johnstone17, Section A1.4]], as well as an instance of Barr’s effective unions [Reference Barr and Borceux1].) We will denote the pairwise disjoint joins by
$\mathrm {Sub}(X)$
. (This notion is part of the definition of coherent category [see, e.g., [Reference Johnstone17, Section A1.4]], as well as an instance of Barr’s effective unions [Reference Barr and Borceux1].) We will denote the pairwise disjoint joins by
![]() $A \sqcup B$
(this is consistent with the above usage by Lemmas 2.1 and 2.2). More generally, we say that
$A \sqcup B$
(this is consistent with the above usage by Lemmas 2.1 and 2.2). More generally, we say that
![]() $\mathsf {C}$
is
$\mathsf {C}$
is
![]() $\kappa $
-subextensive if any
$\kappa $
-subextensive if any
![]() $\kappa $
-ary family of pairwise disjoint
$\kappa $
-ary family of pairwise disjoint
![]() $A_i \subseteq X$
has a pullback-stable join
$A_i \subseteq X$
has a pullback-stable join
![]() $\bigsqcup\nolimits _i A_i$
in
$\bigsqcup\nolimits _i A_i$
in
![]() $\mathrm {Sub}(X)$
. A finitely continuous functor
$\mathrm {Sub}(X)$
. A finitely continuous functor
![]() $\mathcal {F} : \mathsf {C} \to \mathsf {D}$
between finitely complete (
$\mathcal {F} : \mathsf {C} \to \mathsf {D}$
between finitely complete (
![]() $\kappa $
-)subextensive categories is (
$\kappa $
-)subextensive categories is (
![]() $\kappa $
-)subextensive if it preserves the initial object and finite (resp.
$\kappa $
-)subextensive if it preserves the initial object and finite (resp.
![]() $\kappa $
-ary) joins of disjoint subobjects.
$\kappa $
-ary) joins of disjoint subobjects.
The subobject posets
![]() $\mathrm {Sub}(X)$
in a finitely complete
$\mathrm {Sub}(X)$
in a finitely complete
![]() $\kappa $
-subextensive category
$\kappa $
-subextensive category
![]() $\mathsf {C}$
have a partial algebraic structure which we will refer to as a
$\mathsf {C}$
have a partial algebraic structure which we will refer to as a
![]() $\kappa $
-disjunctive frame
Footnote
3
(or distributive disjunctive lattice when
$\kappa $
-disjunctive frame
Footnote
3
(or distributive disjunctive lattice when
![]() $\kappa = \omega $
), meaning a meet-semilattice with (greatest and) least element and joins of pairwise disjoint
$\kappa = \omega $
), meaning a meet-semilattice with (greatest and) least element and joins of pairwise disjoint
![]() $\kappa $
-ary families, over which finite meets distribute; distributivity in
$\kappa $
-ary families, over which finite meets distribute; distributivity in
![]() $\mathrm {Sub}(X)$
follows from pullback-stability. The pullback maps
$\mathrm {Sub}(X)$
follows from pullback-stability. The pullback maps
![]() $f^* : \mathrm {Sub}(Y) \to \mathrm {Sub}(X)$
are
$f^* : \mathrm {Sub}(Y) \to \mathrm {Sub}(X)$
are
![]() $\kappa $
-disjunctive frame homomorphisms (giving a functor
$\kappa $
-disjunctive frame homomorphisms (giving a functor
![]() $\mathrm {Sub} : \mathsf {C}^{\mathrm {op}} \to \mathsf {\kappa DisjFrm}$
to the category of
$\mathrm {Sub} : \mathsf {C}^{\mathrm {op}} \to \mathsf {\kappa DisjFrm}$
to the category of
![]() $\kappa $
-disjunctive frames), as are the maps
$\kappa $
-disjunctive frames), as are the maps
![]() $\mathcal {F}|\mathrm {Sub}_{\mathsf {C}}(X) : \mathrm {Sub}_{\mathsf {C}}(X) \to \mathrm {Sub}_{\mathsf {D}}(\mathcal {F}(X))$
induced by
$\mathcal {F}|\mathrm {Sub}_{\mathsf {C}}(X) : \mathrm {Sub}_{\mathsf {C}}(X) \to \mathrm {Sub}_{\mathsf {D}}(\mathcal {F}(X))$
induced by
![]() $\kappa $
-subextensive functors
$\kappa $
-subextensive functors
![]() $\mathcal {F} : \mathsf {C} \to \mathsf {D}$
.
$\mathcal {F} : \mathsf {C} \to \mathsf {D}$
.
The following facts are standard (see [Reference Johnstone17, Section A1.4]):
Lemma 2.1. A finitely complete
![]() $\kappa $
-extensive category
$\kappa $
-extensive category
![]() $\mathsf {C}$
is
$\mathsf {C}$
is
![]() $\kappa $
-subextensive, with joins of pairwise disjoint subobjects given by their coproduct. Hence, a finitely continuous functor between finitely complete
$\kappa $
-subextensive, with joins of pairwise disjoint subobjects given by their coproduct. Hence, a finitely continuous functor between finitely complete
![]() $\kappa $
-extensive categories is
$\kappa $
-extensive categories is
![]() $\kappa $
-extensive iff it is
$\kappa $
-extensive iff it is
![]() $\kappa $
-subextensive.
$\kappa $
-subextensive.
Proof Let
![]() $A_i \subseteq X \in \mathsf {C}$
for
$A_i \subseteq X \in \mathsf {C}$
for
![]() $i \in I$
,
$i \in I$
,
![]() ${\lvert }{I}{\rvert } < \kappa $
, be pairwise disjoint. It is enough to show that the morphism
${\lvert }{I}{\rvert } < \kappa $
, be pairwise disjoint. It is enough to show that the morphism
![]() $h : \bigsqcup\nolimits _i A_i \to X$
induced by the
$h : \bigsqcup\nolimits _i A_i \to X$
induced by the
![]() $A_i \hookrightarrow X$
via the universal property of the coproduct is monic, for then the universal property easily implies that
$A_i \hookrightarrow X$
via the universal property of the coproduct is monic, for then the universal property easily implies that
![]() $\bigsqcup\nolimits _i A_i$
is the join in
$\bigsqcup\nolimits _i A_i$
is the join in
![]() $\mathrm {Sub}(X)$
, and this join is pullback-stable since the coproduct
$\mathrm {Sub}(X)$
, and this join is pullback-stable since the coproduct
![]() $\bigsqcup\nolimits _i A_i$
is. For this, consider the lower-right pullback square in
$\bigsqcup\nolimits _i A_i$
is. For this, consider the lower-right pullback square in

By pullback-stability of
![]() $\bigsqcup\nolimits _i A_i$
, we may write
$\bigsqcup\nolimits _i A_i$
, we may write
![]() $(\bigsqcup\nolimits _i A_i) \times _X (\bigsqcup\nolimits _i A_i)$
as the coproduct
$(\bigsqcup\nolimits _i A_i) \times _X (\bigsqcup\nolimits _i A_i)$
as the coproduct
For each
![]() $i, j$
,
$i, j$
,
![]() $p^*(A_i) \cap q^*(A_j)$
is the pullback of the composites
$p^*(A_i) \cap q^*(A_j)$
is the pullback of the composites
![]() $A_i, A_j \subseteq \bigsqcup\nolimits _i A_i \xrightarrow {h} X$
, i.e., the inclusions
$A_i, A_j \subseteq \bigsqcup\nolimits _i A_i \xrightarrow {h} X$
, i.e., the inclusions
![]() $A_i, A_j \hookrightarrow X$
, hence is either the diagonal
$A_i, A_j \hookrightarrow X$
, hence is either the diagonal
![]() $A_i \hookrightarrow (\bigsqcup\nolimits _i A_i) \times _X (\bigsqcup\nolimits _i A_i)$
if
$A_i \hookrightarrow (\bigsqcup\nolimits _i A_i) \times _X (\bigsqcup\nolimits _i A_i)$
if
![]() $i = j$
, or
$i = j$
, or
![]() $0$
if
$0$
if
![]() $i \ne j$
. So
$i \ne j$
. So
![]() $(\bigsqcup\nolimits _i A_i) \times _X (\bigsqcup\nolimits _i A_i) = \bigsqcup\nolimits _i A_i$
, i.e., h is monic.
$(\bigsqcup\nolimits _i A_i) \times _X (\bigsqcup\nolimits _i A_i) = \bigsqcup\nolimits _i A_i$
, i.e., h is monic.
Lemma 2.2. Let
![]() $\mathsf {C}$
be a finitely complete
$\mathsf {C}$
be a finitely complete
![]() $\kappa $
-subextensive category,
$\kappa $
-subextensive category,
![]() $X \in \mathsf {C}$
, and
$X \in \mathsf {C}$
, and
![]() $A_i \subseteq X$
be a
$A_i \subseteq X$
be a
![]() $\kappa $
-ary family of pairwise disjoint subobjects. Then their join
$\kappa $
-ary family of pairwise disjoint subobjects. Then their join
![]() $\bigsqcup\nolimits _i A_i$
in
$\bigsqcup\nolimits _i A_i$
in
![]() $\mathrm {Sub}(\mathsf {C})$
is their coproduct in
$\mathrm {Sub}(\mathsf {C})$
is their coproduct in
![]() $\mathsf {C}$
.
$\mathsf {C}$
.
Proof Let
![]() $f_i : A_i \to Y \in \mathsf {C}$
; we must find a unique
$f_i : A_i \to Y \in \mathsf {C}$
; we must find a unique
![]() $f : \bigsqcup\nolimits _i A_i \to Y$
such that
$f : \bigsqcup\nolimits _i A_i \to Y$
such that
![]() $f|A_i = f_i$
for each i. In any finitely complete category, morphisms
$f|A_i = f_i$
for each i. In any finitely complete category, morphisms
![]() $f : X \to Y$
are in bijection with their graphs
$f : X \to Y$
are in bijection with their graphs
![]() $(1_X, f) : X \hookrightarrow X \times Y$
, which are subobjects
$(1_X, f) : X \hookrightarrow X \times Y$
, which are subobjects
![]() $G \subseteq X \times Y$
whose composite with the first projection
$G \subseteq X \times Y$
whose composite with the first projection
![]() $X \times Y \to X$
is an isomorphism. For our desired
$X \times Y \to X$
is an isomorphism. For our desired
![]() $f : \bigsqcup\nolimits _i A_i \to Y$
, letting
$f : \bigsqcup\nolimits _i A_i \to Y$
, letting
![]() $G \subseteq (\bigsqcup\nolimits _i A_i) \times Y$
be its graph, the condition
$G \subseteq (\bigsqcup\nolimits _i A_i) \times Y$
be its graph, the condition
![]() $f|A_i = f_i$
is easily seen to be equivalent to
$f|A_i = f_i$
is easily seen to be equivalent to
![]() $G \cap (A_i \times Y)$
being the graph
$G \cap (A_i \times Y)$
being the graph
![]() $G_i$
of
$G_i$
of
![]() $f_i$
for each i. Since
$f_i$
for each i. Since
![]() $(\bigsqcup\nolimits _i A_i) \times Y = \bigsqcup\nolimits _i (A_i \times Y)$
by pullback-stability of the join
$(\bigsqcup\nolimits _i A_i) \times Y = \bigsqcup\nolimits _i (A_i \times Y)$
by pullback-stability of the join
![]() $\bigsqcup\nolimits _i A_i$
(under the projection
$\bigsqcup\nolimits _i A_i$
(under the projection
![]() $(\bigsqcup\nolimits _i A_i) \times Y \to \bigsqcup\nolimits _i A_i$
), we must have (by distributivity)
$(\bigsqcup\nolimits _i A_i) \times Y \to \bigsqcup\nolimits _i A_i$
), we must have (by distributivity)
![]() $G = G \cap \bigsqcup\nolimits _i (A_i \times Y) = \bigsqcup\nolimits _i (G \cap (A_i \times Y)) = \bigsqcup\nolimits _i G_i$
, which determines G as a subobject of
$G = G \cap \bigsqcup\nolimits _i (A_i \times Y) = \bigsqcup\nolimits _i (G \cap (A_i \times Y)) = \bigsqcup\nolimits _i G_i$
, which determines G as a subobject of
![]() $(\bigsqcup\nolimits _i A_i) \times Y$
. It remains only to check that G is a graph. The composite
$(\bigsqcup\nolimits _i A_i) \times Y$
. It remains only to check that G is a graph. The composite
![]() $G \hookrightarrow (\bigsqcup\nolimits _i A_i) \times Y \to \bigsqcup\nolimits _i A_i$
is monic, since its pullback with itself is the subobject
$G \hookrightarrow (\bigsqcup\nolimits _i A_i) \times Y \to \bigsqcup\nolimits _i A_i$
is monic, since its pullback with itself is the subobject
![]() $p^*(G) \cap q^*(G) \subseteq (\bigsqcup\nolimits _i A_i) \times Y \times Y$
in the pullback diagram
$p^*(G) \cap q^*(G) \subseteq (\bigsqcup\nolimits _i A_i) \times Y \times Y$
in the pullback diagram

and we have
![]() $p^*(G) \cap q^*(G) = \bigsqcup\nolimits _{i,j} (p^*(G_i) \cap q^*(G_j))$
(by pullback-stability of the join
$p^*(G) \cap q^*(G) = \bigsqcup\nolimits _{i,j} (p^*(G_i) \cap q^*(G_j))$
(by pullback-stability of the join
![]() $G = \bigsqcup\nolimits _i G_i$
and distributivity) which is easily seen to be the diagonal of
$G = \bigsqcup\nolimits _i G_i$
and distributivity) which is easily seen to be the diagonal of
![]() $G = \bigsqcup\nolimits _i G_i$
using that each
$G = \bigsqcup\nolimits _i G_i$
using that each
![]() $G_i$
is a graph and their domains
$G_i$
is a graph and their domains
![]() $A_i \subseteq \bigsqcup\nolimits _i A_i$
are disjoint. And the composite
$A_i \subseteq \bigsqcup\nolimits _i A_i$
are disjoint. And the composite
![]() $G \hookrightarrow (\bigsqcup\nolimits _i A_i) \times Y \to \bigsqcup\nolimits _i A_i$
as a subobject is all of
$G \hookrightarrow (\bigsqcup\nolimits _i A_i) \times Y \to \bigsqcup\nolimits _i A_i$
as a subobject is all of
![]() $\bigsqcup\nolimits _i A_i$
, since it contains each
$\bigsqcup\nolimits _i A_i$
, since it contains each
![]() $A_i$
, since G contains
$A_i$
, since G contains
![]() $G_i$
and
$G_i$
and
![]() $G_i$
is a graph.
$G_i$
is a graph.
Corollary 2.3. A finitely complete
![]() $\kappa $
-subextensive category
$\kappa $
-subextensive category
![]() $\mathsf {C}$
in which every
$\mathsf {C}$
in which every
![]() $\kappa $
-ary family of objects
$\kappa $
-ary family of objects
![]() $X_i$
jointly embed as pairwise disjoint subobjects of some other object Y is
$X_i$
jointly embed as pairwise disjoint subobjects of some other object Y is
![]() $\kappa $
-extensive, with the coproduct
$\kappa $
-extensive, with the coproduct
![]() $\bigsqcup\nolimits _i X_i$
given by the join in
$\bigsqcup\nolimits _i X_i$
given by the join in
![]() $\mathrm {Sub}(Y)$
.
$\mathrm {Sub}(Y)$
.
In a distributive disjunctive lattice A, with least and greatest elements
![]() $\bot , \top $
and meets and disjoint joins denoted
$\bot , \top $
and meets and disjoint joins denoted
![]() $\wedge , \vee $
, we may already define the familiar (in distributive lattices) notion of complement of
$\wedge , \vee $
, we may already define the familiar (in distributive lattices) notion of complement of
![]() $a \in A$
, i.e., any
$a \in A$
, i.e., any
![]() $b \in A$
such that
$b \in A$
such that
![]() $a \wedge b = \bot $
and
$a \wedge b = \bot $
and
![]() $a \vee b = \top $
. Complements are unique, since if
$a \vee b = \top $
. Complements are unique, since if
![]() $b, c$
are complements of a, then
$b, c$
are complements of a, then
![]() $b = b \wedge (a \vee c) = (b \wedge a) \vee (b \wedge c) = b \wedge c \le c$
. So we may denote the complement of a, if it exists, by
$b = b \wedge (a \vee c) = (b \wedge a) \vee (b \wedge c) = b \wedge c \le c$
. So we may denote the complement of a, if it exists, by
![]() $\neg a$
, and complements are automatically preserved by distributive disjunctive lattice homomorphisms.
$\neg a$
, and complements are automatically preserved by distributive disjunctive lattice homomorphisms.
Lemma 2.4. A distributive disjunctive lattice A with all complements is a Boolean algebra.
Proof Let
![]() $a, b \in A$
. Then
$a, b \in A$
. Then
![]() $a \wedge \neg a \wedge b = \bot $
, so the join
$a \wedge \neg a \wedge b = \bot $
, so the join
![]() $a \vee (\neg a \wedge b)$
exists, and meets distribute over it. Clearly,
$a \vee (\neg a \wedge b)$
exists, and meets distribute over it. Clearly,
![]() $a \le a \vee (\neg a \wedge b)$
, and for any
$a \le a \vee (\neg a \wedge b)$
, and for any
![]() $c \ge a, b$
, we have
$c \ge a, b$
, we have
![]() $c \ge a, \neg a \wedge b$
whence
$c \ge a, \neg a \wedge b$
whence
![]() $c \ge a \vee (\neg a \wedge b)$
; we also have
$c \ge a \vee (\neg a \wedge b)$
; we also have
![]() $b \wedge (a \vee (\neg a \wedge b)) = (b \wedge a) \vee (b \wedge \neg a) = b \wedge (a \vee \neg a) = b$
, i.e.,
$b \wedge (a \vee (\neg a \wedge b)) = (b \wedge a) \vee (b \wedge \neg a) = b \wedge (a \vee \neg a) = b$
, i.e.,
![]() $b \le a \vee (\neg a \wedge b)$
, whence
$b \le a \vee (\neg a \wedge b)$
, whence
![]() $a \vee (\neg a \wedge b)$
is the join
$a \vee (\neg a \wedge b)$
is the join
![]() $a \vee b$
of
$a \vee b$
of
![]() $a, b$
. For any
$a, b$
. For any
![]() $c \in A$
, we have
$c \in A$
, we have
![]() $c \wedge (a \vee b) = c \wedge (a \vee (\neg a \wedge b)) = (c \wedge a) \vee (c \wedge \neg a \wedge b) \le (c \wedge a) \vee (c \wedge b)$
, so A is a distributive lattice.
$c \wedge (a \vee b) = c \wedge (a \vee (\neg a \wedge b)) = (c \wedge a) \vee (c \wedge \neg a \wedge b) \le (c \wedge a) \vee (c \wedge b)$
, so A is a distributive lattice.
We call a finitely complete
![]() $\kappa $
-subextensive category
$\kappa $
-subextensive category
![]() $\mathsf {C}$
Boolean if each of its subobject
$\mathsf {C}$
Boolean if each of its subobject
![]() $\kappa $
-disjunctive frames
$\kappa $
-disjunctive frames
![]() $\mathrm {Sub}(X)$
is a (
$\mathrm {Sub}(X)$
is a (
![]() $\kappa $
-complete) Boolean algebra. (We will discuss
$\kappa $
-complete) Boolean algebra. (We will discuss
![]() $\kappa $
-complete Boolean algebras in more detail in the next section.) For such
$\kappa $
-complete Boolean algebras in more detail in the next section.) For such
![]() $\mathsf {C}$
, the pullback maps between subobject lattices are (
$\mathsf {C}$
, the pullback maps between subobject lattices are (
![]() $\kappa $
-)Boolean homomorphisms, and a finitely continuous
$\kappa $
-)Boolean homomorphisms, and a finitely continuous
![]() $\kappa $
-(sub)extensive functor
$\kappa $
-(sub)extensive functor
![]() $\mathcal {F} : \mathsf {C} \to \mathsf {D}$
between two such
$\mathcal {F} : \mathsf {C} \to \mathsf {D}$
between two such
![]() $\mathsf {C}, \mathsf {D}$
preserves complements of subobjects. Note also that if
$\mathsf {C}, \mathsf {D}$
preserves complements of subobjects. Note also that if
![]() $\mathsf {C}$
is
$\mathsf {C}$
is
![]() $\kappa $
-complete Boolean subextensive, then it is
$\kappa $
-complete Boolean subextensive, then it is
![]() $\kappa $
-subextensive, since its subobject Boolean algebras have
$\kappa $
-subextensive, since its subobject Boolean algebras have
![]() $\kappa $
-ary meets, hence
$\kappa $
-ary meets, hence
![]() $\kappa $
-ary joins (which are pullback-stable, since
$\kappa $
-ary joins (which are pullback-stable, since
![]() $\kappa $
-ary meets and complements are).
$\kappa $
-ary meets and complements are).
Lemma 2.5. A
![]() $\kappa $
-complete Boolean extensive category
$\kappa $
-complete Boolean extensive category
![]() $\mathsf {C}$
is
$\mathsf {C}$
is
![]() $\kappa $
-extensive.
$\kappa $
-extensive.
Proof Since
![]() $\mathsf {C}$
is
$\mathsf {C}$
is
![]() $\kappa $
-subextensive, by Corollary 2.3, it is enough to show that any
$\kappa $
-subextensive, by Corollary 2.3, it is enough to show that any
![]() $\kappa $
-ary family of objects
$\kappa $
-ary family of objects
![]() $X_i \in \mathsf {C}$
can be jointly embedded as pairwise disjoint subobjects of some other object. Consider
$X_i \in \mathsf {C}$
can be jointly embedded as pairwise disjoint subobjects of some other object. Consider
![]() $f_i := (f_{ij})_j : X_i \to \prod _j (X_j \sqcup 1)$
for each i, where
$f_i := (f_{ij})_j : X_i \to \prod _j (X_j \sqcup 1)$
for each i, where
![]() $f_{ii} : X_i \hookrightarrow X_i \sqcup 1$
is the coproduct injection and
$f_{ii} : X_i \hookrightarrow X_i \sqcup 1$
is the coproduct injection and
![]() $f_{ij} : X_i \to 1 \hookrightarrow X_j \sqcup 1$
for
$f_{ij} : X_i \to 1 \hookrightarrow X_j \sqcup 1$
for
![]() $j \ne i$
. Each
$j \ne i$
. Each
![]() $f_i$
is monic, since its composition with the ith projection
$f_i$
is monic, since its composition with the ith projection
![]() $\pi _i : \prod _j (X_j \sqcup 1) \to X_i \sqcup 1$
is
$\pi _i : \prod _j (X_j \sqcup 1) \to X_i \sqcup 1$
is
![]() $f_{ii} : X_i \hookrightarrow X_i \sqcup 1$
, and for
$f_{ii} : X_i \hookrightarrow X_i \sqcup 1$
, and for
![]() $i \ne j$
, we have a commutative diagram
$i \ne j$
, we have a commutative diagram

whence the pullback of the top row maps into the pullback of the bottom row which is
![]() $0$
.
$0$
.
The natural framework for studying categories equipped with algebraic structure (e.g., extensive categories and the above variations) is that of 2-categories. We will quickly review the basic notions needed in this paper (see [Reference Borceux3, I Chapter 7], [Reference Johnstone17, Section B1.1] for more comprehensive background).
A 2-category, denoted by a Fraktur symbol like
![]() $\mathfrak {C}$
, consists of objects
$\mathfrak {C}$
, consists of objects
![]() $\mathsf {X} \in \mathfrak {C}$
, together with for each pair of objects
$\mathsf {X} \in \mathfrak {C}$
, together with for each pair of objects
![]() $\mathsf {X}, \mathsf {Y} \in \mathfrak {C}$
a hom-category
$\mathsf {X}, \mathsf {Y} \in \mathfrak {C}$
a hom-category
![]() $\mathfrak {C}(\mathsf {X}, \mathsf {Y})$
, whose objects
$\mathfrak {C}(\mathsf {X}, \mathsf {Y})$
, whose objects
![]() $\mathcal {F} \in \mathfrak {C}(\mathsf {X}, \mathsf {Y})$
are called morphisms
$\mathcal {F} \in \mathfrak {C}(\mathsf {X}, \mathsf {Y})$
are called morphisms
![]() $\mathcal {F} : \mathsf {X} \to \mathsf {Y}$
of
$\mathcal {F} : \mathsf {X} \to \mathsf {Y}$
of
![]() $\mathfrak {C}$
and morphisms
$\mathfrak {C}$
and morphisms
![]() $\theta : \mathcal {F} \to \mathcal {G} \in \mathfrak {C}(\mathsf {X}, \mathsf {Y})$
are called 2-cells
$\theta : \mathcal {F} \to \mathcal {G} \in \mathfrak {C}(\mathsf {X}, \mathsf {Y})$
are called 2-cells
![]() $\theta : \mathcal {F} \to \mathcal {G} : \mathsf {X} \to \mathsf {Y}$
of
$\theta : \mathcal {F} \to \mathcal {G} : \mathsf {X} \to \mathsf {Y}$
of
![]() $\mathfrak {C}$
, together with for each
$\mathfrak {C}$
, together with for each
![]() $\mathsf {X} \in \mathfrak {C}$
an identity morphism
$\mathsf {X} \in \mathfrak {C}$
an identity morphism
![]() $1_{\mathsf {X}} \in \mathfrak {C}(\mathsf {X}, \mathsf {X})$
and for each
$1_{\mathsf {X}} \in \mathfrak {C}(\mathsf {X}, \mathsf {X})$
and for each
![]() $\mathsf {X}, \mathsf {Y}, \mathsf {Z} \in \mathfrak {C}$
a composition functor
$\mathsf {X}, \mathsf {Y}, \mathsf {Z} \in \mathfrak {C}$
a composition functor
![]() $\mathfrak {C}(\mathsf {Y}, \mathsf {Z}) \times \mathfrak {C}(\mathsf {X}, \mathsf {Y}) \to \mathfrak {C}(\mathsf {X}, \mathsf {Z})$
, obeying the usual associativity and unitality laws (on the nose, not just up to natural isomorphism of functors). A (strict) 2-functor between 2-categories is a map taking objects to objects, morphisms to morphisms, and 2-cells to 2-cells (with the obvious endpoint compatibility conditions), which is a functor on each hom-category and also preserves the global composition and identity.
$\mathfrak {C}(\mathsf {Y}, \mathsf {Z}) \times \mathfrak {C}(\mathsf {X}, \mathsf {Y}) \to \mathfrak {C}(\mathsf {X}, \mathsf {Z})$
, obeying the usual associativity and unitality laws (on the nose, not just up to natural isomorphism of functors). A (strict) 2-functor between 2-categories is a map taking objects to objects, morphisms to morphisms, and 2-cells to 2-cells (with the obvious endpoint compatibility conditions), which is a functor on each hom-category and also preserves the global composition and identity.
The quintessential example of a 2-category is
![]() $\mathfrak {Cat}$
, whose objects are (small)Footnote
4
categories, morphisms are functors, and 2-cells are natural transformations; that is, each hom-category
$\mathfrak {Cat}$
, whose objects are (small)Footnote
4
categories, morphisms are functors, and 2-cells are natural transformations; that is, each hom-category
![]() $\mathfrak {Cat}(\mathsf {C}, \mathsf {D})$
is the functor category
$\mathfrak {Cat}(\mathsf {C}, \mathsf {D})$
is the functor category
![]() $\mathsf {D}^{\mathsf {C}}$
. We will consider the following sub-2-categories of
$\mathsf {D}^{\mathsf {C}}$
. We will consider the following sub-2-categories of
![]() $\mathfrak {Cat}$
, consisting of categories with algebraic structure and functors preserving said structure. Let
$\mathfrak {Cat}$
, consisting of categories with algebraic structure and functors preserving said structure. Let
![]() $\kappa \mathfrak {LimCat} \subseteq \mathfrak {Cat}$
be the sub-2-category of
$\kappa \mathfrak {LimCat} \subseteq \mathfrak {Cat}$
be the sub-2-category of
![]() $\kappa $
-complete categories,
$\kappa $
-complete categories,
![]() $\kappa $
-continuous functors, and (all) natural transformations. Let
$\kappa $
-continuous functors, and (all) natural transformations. Let
be the further sub-2-categories of
![]() $\kappa $
-complete (Boolean) (
$\kappa $
-complete (Boolean) (
![]() $\kappa $
-)(sub)extensive categories,
$\kappa $
-)(sub)extensive categories,
![]() $\kappa $
-continuous (
$\kappa $
-continuous (
![]() $\kappa $
-)(sub)extensive functors, and natural transformations. For example,
$\kappa $
-)(sub)extensive functors, and natural transformations. For example,
![]() $\kappa \mathfrak {LimBSExtCat}$
is the 2-category of
$\kappa \mathfrak {LimBSExtCat}$
is the 2-category of
![]() $\kappa $
-complete Boolean subextensive categories and
$\kappa $
-complete Boolean subextensive categories and
![]() $\kappa $
-continuous subextensive functors. These are related as follows:
$\kappa $
-continuous subextensive functors. These are related as follows:

The
![]() $\rightarrowtail $
’s denote full sub-2-categories, i.e., the sub-2-category includes all functors in the bigger 2-category between two objects in the sub-2-category. For the horizontal
$\rightarrowtail $
’s denote full sub-2-categories, i.e., the sub-2-category includes all functors in the bigger 2-category between two objects in the sub-2-category. For the horizontal
![]() $\rightarrowtail $
’s, fullness is by Lemma 2.1. For the vertical
$\rightarrowtail $
’s, fullness is by Lemma 2.1. For the vertical
![]() $\rightarrowtail $
’s, fullness is by definition (subextensive functors automatically preserve complements of subobjects). The diagonal equalities in the top layer are by Lemma 2.5 and the sentence preceding it; we will use the shorter names for these two 2-categories, which are the focus of this paper.
$\rightarrowtail $
’s, fullness is by definition (subextensive functors automatically preserve complements of subobjects). The diagonal equalities in the top layer are by Lemma 2.5 and the sentence preceding it; we will use the shorter names for these two 2-categories, which are the focus of this paper.
Because categorical structure (e.g., limits) is often only defined up to canonical isomorphism, the “correct” 2-categorical analog of a (1-)categorical notion often involves weakening a naive analog by replacing some equalities with coherent isomorphisms. For example, the notion of (strict) 2-functor from above, while useful, is not general enough to include many naturally occurring examples, and must be weakened to the notion of pseudofunctor (where composition is preserved only up to coherent isomorphism; see [Reference Borceux3, Section I 7.5], [Reference Johnstone17, Section B1.1]). Similarly, the universal property of limits and colimits must be weakened by relaxing the uniqueness condition in order to arrive at what are commonly called bi(co)limits (see [Reference Borceux3, Section I 7.4]). Indeed, it is known that 2-categories of categories with “nice” algebraic structure (such as those above) generally lack colimits in the naive (strict) sense, although they admit all bicolimits (see [Reference Blackwell, Kelly and Power2]).
In this paper, we will only need one simple instance of a non-strict 2-categorical notion: that of a (bi-)initial object (we henceforth drop the “bi” prefix)
![]() $\mathsf {X}$
in a 2-category
$\mathsf {X}$
in a 2-category
![]() $\mathfrak {C}$
, which is an object such that for any other
$\mathfrak {C}$
, which is an object such that for any other
![]() $\mathsf {Y} \in \mathfrak {C}$
, the hom-category
$\mathsf {Y} \in \mathfrak {C}$
, the hom-category
![]() $\mathfrak {C}(\mathsf {X}, \mathsf {Y})$
is equivalent to the terminal category. This means that for any other
$\mathfrak {C}(\mathsf {X}, \mathsf {Y})$
is equivalent to the terminal category. This means that for any other
![]() $\mathsf {Y}$
, there is a morphism
$\mathsf {Y}$
, there is a morphism
![]() $\mathsf {X} \to \mathsf {Y}$
, and for any two such morphisms
$\mathsf {X} \to \mathsf {Y}$
, and for any two such morphisms
![]() $\mathcal {F}, \mathcal {G} : \mathsf {X} \to \mathsf {Y}$
, there is a unique 2-cell
$\mathcal {F}, \mathcal {G} : \mathsf {X} \to \mathsf {Y}$
, there is a unique 2-cell
![]() $\mathcal {F} \to \mathcal {G}$
(which must thus be an isomorphism). Equivalently, this means
$\mathcal {F} \to \mathcal {G}$
(which must thus be an isomorphism). Equivalently, this means
![]() $\mathsf {X}$
admits a morphism to any other object, and this morphism is unique up to unique (2-cell) isomorphism and has no non-identity 2-cells to itself. In particular, an initial object
$\mathsf {X}$
admits a morphism to any other object, and this morphism is unique up to unique (2-cell) isomorphism and has no non-identity 2-cells to itself. In particular, an initial object
![]() $\mathsf {X} \in \mathfrak {C}$
is unique up to equivalence in
$\mathsf {X} \in \mathfrak {C}$
is unique up to equivalence in
![]() $\mathfrak {C}$
(with the equivalence being itself unique up to unique isomorphism).
$\mathfrak {C}$
(with the equivalence being itself unique up to unique isomorphism).
For example, an initial object in
![]() $\kappa \mathfrak {LimBExtCat}$
, as provided by Theorem 1.2, is a
$\kappa \mathfrak {LimBExtCat}$
, as provided by Theorem 1.2, is a
![]() $\kappa $
-complete Boolean extensive category
$\kappa $
-complete Boolean extensive category
![]() $\mathsf {C}$
, such that for any other
$\mathsf {C}$
, such that for any other
![]() $\kappa $
-complete Boolean extensive category
$\kappa $
-complete Boolean extensive category
![]() $\mathsf {D}$
, there is a
$\mathsf {D}$
, there is a
![]() $\kappa $
-continuous extensive functor
$\kappa $
-continuous extensive functor
![]() $\mathcal {F} : \mathsf {C} \to \mathsf {D}$
, which is unique up to unique natural isomorphism, and admits no non-identity natural transformations
$\mathcal {F} : \mathsf {C} \to \mathsf {D}$
, which is unique up to unique natural isomorphism, and admits no non-identity natural transformations
![]() $\mathcal {F} \to \mathcal {F}$
. Such
$\mathcal {F} \to \mathcal {F}$
. Such
![]() $\mathsf {C}$
, if it exists, is unique up to (unique-up-to-unique-isomorphism) equivalence of categories.
$\mathsf {C}$
, if it exists, is unique up to (unique-up-to-unique-isomorphism) equivalence of categories.
3
 $\kappa $
-Boolean algebras
$\kappa $
-Boolean algebras
For general background on Boolean algebras, see, e.g., [Reference Sikorski27]. We denote Boolean operations by
![]() $\wedge , \vee , \neg , \top , \bot $
, and also use the implication operation
$\wedge , \vee , \neg , \top , \bot $
, and also use the implication operation
![]() $a \to b := \neg a \vee b$
and bi-implication
$a \to b := \neg a \vee b$
and bi-implication
![]() $a \leftrightarrow b := (a \to b) \wedge (b \to a)$
. We will never denote
$a \leftrightarrow b := (a \to b) \wedge (b \to a)$
. We will never denote
![]() $\top , \bot $
by
$\top , \bot $
by
![]() $1, 0$
(which are reserved for generating elements of free algebras over finite cardinals).
$1, 0$
(which are reserved for generating elements of free algebras over finite cardinals).
A
![]() $\kappa $
-(complete)Boolean algebra is a Boolean algebra with
$\kappa $
-(complete)Boolean algebra is a Boolean algebra with
![]() $\kappa $
-ary joins (hence
$\kappa $
-ary joins (hence
![]() $\kappa $
-ary meets). Let
$\kappa $
-ary meets). Let
![]() $\kappa \mathsf {Bool}$
denote the category of
$\kappa \mathsf {Bool}$
denote the category of
![]() $\kappa $
-Boolean algebras and (
$\kappa $
-Boolean algebras and (
![]() $\kappa $
-join-preserving) homomorphisms.
$\kappa $
-join-preserving) homomorphisms.
![]() $\kappa $
-Boolean algebras are defined by a
$\kappa $
-Boolean algebras are defined by a
![]() $\kappa $
-ary (infinitary) algebraic theory, whence
$\kappa $
-ary (infinitary) algebraic theory, whence
![]() $\kappa \mathsf {Bool}$
is a well-behaved “algebraic” (i.e., monadic over
$\kappa \mathsf {Bool}$
is a well-behaved “algebraic” (i.e., monadic over
![]() $\mathsf {Set}$
) category, in particular having all small limits and colimits (see, e.g., [Reference Borceux3, II Section 4.3]). We will denote binary coproducts in
$\mathsf {Set}$
) category, in particular having all small limits and colimits (see, e.g., [Reference Borceux3, II Section 4.3]). We will denote binary coproducts in
![]() $\kappa \mathsf {Bool}$
by
$\kappa \mathsf {Bool}$
by
![]() $A \otimes B$
, and more generally, the pushout of
$A \otimes B$
, and more generally, the pushout of
![]() $B, C$
over A by
$B, C$
over A by
![]() $B \otimes _A C$
.Footnote
5
$B \otimes _A C$
.Footnote
5
For each set X, let
![]() $\mathcal {K}(X)$
denote the free
$\mathcal {K}(X)$
denote the free
![]() $\kappa $
-Boolean algebra generated by X. We identify the elements of X with the generators in
$\kappa $
-Boolean algebra generated by X. We identify the elements of X with the generators in
![]() $\mathcal {K}(X)$
, so that
$\mathcal {K}(X)$
, so that
![]() $X \subseteq \mathcal {K}(X)$
. For a map
$X \subseteq \mathcal {K}(X)$
. For a map
![]() $f : X \to Y$
, let
$f : X \to Y$
, let
![]() $\mathcal {K}(f) = f_* : \mathcal {K}(X) \to \mathcal {K}(Y)$
be the
$\mathcal {K}(f) = f_* : \mathcal {K}(X) \to \mathcal {K}(Y)$
be the
![]() $\kappa $
-Boolean extension of f. Thus
$\kappa $
-Boolean extension of f. Thus
![]() $\mathcal {K} : \mathsf {Set} \to \kappa \mathsf {Bool}$
is the free
$\mathcal {K} : \mathsf {Set} \to \kappa \mathsf {Bool}$
is the free
![]() $\kappa $
-Boolean algebra functor, left adjoint to the forgetful functor
$\kappa $
-Boolean algebra functor, left adjoint to the forgetful functor
![]() $\kappa \mathsf {Bool} \to \mathsf {Set}$
.
$\kappa \mathsf {Bool} \to \mathsf {Set}$
.
Let
![]() $\kappa \mathsf {Bool}_{\kappa } \subseteq \kappa \mathsf {Bool}$
denote the full subcategory of
$\kappa \mathsf {Bool}_{\kappa } \subseteq \kappa \mathsf {Bool}$
denote the full subcategory of
![]() $\kappa $
-presented
$\kappa $
-presented
![]() $\kappa $
-Boolean algebras, i.e.,
$\kappa $
-Boolean algebras, i.e.,
![]() $\kappa $
-Boolean algebras (isomorphic to ones) of the form
$\kappa $
-Boolean algebras (isomorphic to ones) of the form
![]() $\mathcal {K}(X)/{\sim }$
for some
$\mathcal {K}(X)/{\sim }$
for some
![]() $X \in \mathsf {Set}_{\kappa }$
and some
$X \in \mathsf {Set}_{\kappa }$
and some
![]() $\kappa $
-generated
$\kappa $
-generated
![]() $\kappa $
-Boolean algebra congruence relation
$\kappa $
-Boolean algebra congruence relation
![]() ${\sim } \subseteq \mathcal {K}(X)^2$
.
${\sim } \subseteq \mathcal {K}(X)^2$
.
The following algebraic fact is standard:
Lemma 3.1. Let A be a
![]() $\kappa $
-presented
$\kappa $
-presented
![]() $\kappa $
-Boolean algebra, and let
$\kappa $
-Boolean algebra, and let
![]() $X \subseteq A$
be
$X \subseteq A$
be
![]() $< \kappa $
-many generators. Then A has a
$< \kappa $
-many generators. Then A has a
![]() $\kappa $
-ary presentation using only the generators in X, i.e., the congruence kernel of the canonical homomorphism
$\kappa $
-ary presentation using only the generators in X, i.e., the congruence kernel of the canonical homomorphism
![]() $p : \mathcal {K}(X) \twoheadrightarrow A$
is
$p : \mathcal {K}(X) \twoheadrightarrow A$
is
![]() $\kappa $
-generated.
$\kappa $
-generated.
Proof Let
![]() $q : \mathcal {K}(Y) \twoheadrightarrow \mathcal {K}(Y)/{\sim } \cong A$
be some
$q : \mathcal {K}(Y) \twoheadrightarrow \mathcal {K}(Y)/{\sim } \cong A$
be some
![]() $\kappa $
-ary presentation, with
$\kappa $
-ary presentation, with
![]() ${\sim } = \ker (q) \ \kappa $
-generated, say by pairs
${\sim } = \ker (q) \ \kappa $
-generated, say by pairs
![]() $s_i \sim t_i$
for
$s_i \sim t_i$
for
![]() $i \in I$
(
$i \in I$
(
![]() ${\lvert }{I}{\rvert } < \kappa $
) where
${\lvert }{I}{\rvert } < \kappa $
) where
![]() $s_i, t_i \in \mathcal {K}(Y)$
. For each
$s_i, t_i \in \mathcal {K}(Y)$
. For each
![]() $x \in X$
, pick some
$x \in X$
, pick some
![]() $u(x) \in q^{-1}(x) \subseteq \mathcal {K}(Y)$
, and for each
$u(x) \in q^{-1}(x) \subseteq \mathcal {K}(Y)$
, and for each
![]() $y \in Y$
, pick some
$y \in Y$
, pick some
![]() $v(y) \in p^{-1}(y) \subseteq \mathcal {K}(X)$
. Extend
$v(y) \in p^{-1}(y) \subseteq \mathcal {K}(X)$
. Extend
![]() $u, v$
to homomorphisms
$u, v$
to homomorphisms
![]() $u : \mathcal {K}(X) \to \mathcal {K}(Y)$
and
$u : \mathcal {K}(X) \to \mathcal {K}(Y)$
and
![]() $v : \mathcal {K}(Y) \to \mathcal {K}(X)$
. Then it is straightforward to see that
$v : \mathcal {K}(Y) \to \mathcal {K}(X)$
. Then it is straightforward to see that
![]() $\ker (p) = {\approx }$
, where
$\ker (p) = {\approx }$
, where
![]() $\approx $
is the congruence on
$\approx $
is the congruence on
![]() $\mathcal {K}(X)$
generated by
$\mathcal {K}(X)$
generated by
![]() $v(s_i) \approx v(t_i)$
and
$v(s_i) \approx v(t_i)$
and
![]() $x \approx v(u(x))$
.
$x \approx v(u(x))$
.
It is a standard fact that a congruence
![]() ${\sim }$
on a
${\sim }$
on a
![]() $\kappa $
-Boolean algebra A is determined by the congruence class
$\kappa $
-Boolean algebra A is determined by the congruence class
![]() $[\top ]_{\sim } \subseteq A$
, which is an arbitrary
$[\top ]_{\sim } \subseteq A$
, which is an arbitrary
![]() $\kappa $
-filter on A, and
$\kappa $
-filter on A, and
![]() $\sim $
is
$\sim $
is
![]() $\kappa $
-generated iff
$\kappa $
-generated iff
![]() $[\top ]_{\sim }$
is a principal filter
$[\top ]_{\sim }$
is a principal filter
![]() ${\uparrow } a$
(in which case
${\uparrow } a$
(in which case
![]() $\sim $
is generated by the single pair
$\sim $
is generated by the single pair
![]() $\top \sim a$
, and we can take
$\top \sim a$
, and we can take
![]() $a := \bigwedge\nolimits_i (b_i \leftrightarrow c_i)$
for some
$a := \bigwedge\nolimits_i (b_i \leftrightarrow c_i)$
for some
![]() $\kappa $
-ary family of generators
$\kappa $
-ary family of generators
![]() $b_i \sim c_i$
of
$b_i \sim c_i$
of
![]() $\sim $
). For
$\sim $
). For
![]() $a \in A$
, we denote by
$a \in A$
, we denote by
![]() $A/a$
the quotient by the congruence
$A/a$
the quotient by the congruence
![]() ${\langle }{(\top , a)}{\rangle }\subseteq A^2$
corresponding to the principal filter
${\langle }{(\top , a)}{\rangle }\subseteq A^2$
corresponding to the principal filter
![]() ${\uparrow } a$
. Note that
${\uparrow } a$
. Note that
![]() $A/a$
can be identified with the principal ideal
$A/a$
can be identified with the principal ideal
![]() ${\downarrow } a \subseteq A$
via the isomorphism
${\downarrow } a \subseteq A$
via the isomorphism
![]() ${\downarrow } a \hookrightarrow A \twoheadrightarrow A/a$
; the quotient map is then identified with
${\downarrow } a \hookrightarrow A \twoheadrightarrow A/a$
; the quotient map is then identified with
![]() $a \wedge (-) : A \twoheadrightarrow {\downarrow } a$
. Thus for
$a \wedge (-) : A \twoheadrightarrow {\downarrow } a$
. Thus for
![]() $\kappa $
-presented A, we have bijections
$\kappa $
-presented A, we have bijections
 $$ \begin{align*} A &\cong \{\kappa\text{-generated congruences on } A\} \hspace{-20pt}&&\cong \{\kappa\text{-presented quotients of } A\} \\ a &\mapsto {\langle}{(\top, a)}{\rangle} &&\mapsto A/a \cong {\downarrow} a\,, \end{align*} $$
$$ \begin{align*} A &\cong \{\kappa\text{-generated congruences on } A\} \hspace{-20pt}&&\cong \{\kappa\text{-presented quotients of } A\} \\ a &\mapsto {\langle}{(\top, a)}{\rangle} &&\mapsto A/a \cong {\downarrow} a\,, \end{align*} $$
where the second
![]() $\cong $
is by Lemma 3.1, and the first
$\cong $
is by Lemma 3.1, and the first
![]() $\cong $
is order-reversing. Note, furthermore, that these bijections are compatible with homomorphisms, in the sense that for
$\cong $
is order-reversing. Note, furthermore, that these bijections are compatible with homomorphisms, in the sense that for
![]() $f : A \to B \in \kappa \mathsf {Bool}_{\kappa }$
and
$f : A \to B \in \kappa \mathsf {Bool}_{\kappa }$
and
![]() $a \in A$
,
$a \in A$
,
![]() $B/f(a)$
is the pushout of f and
$B/f(a)$
is the pushout of f and
![]() $A/a$
:
$A/a$
:

Recall that in algebraic categories such as
![]() $\kappa \mathsf {Bool}$
, surjective homomorphisms are precisely the regular epimorphisms (epimorphisms which are the coequalizer of some parallel pair of morphisms; see, e.g., [Reference Borceux3, II Theorem 4.3.5]). Lagrange [Reference Lagrange19] showed that in
$\kappa \mathsf {Bool}$
, surjective homomorphisms are precisely the regular epimorphisms (epimorphisms which are the coequalizer of some parallel pair of morphisms; see, e.g., [Reference Borceux3, II Theorem 4.3.5]). Lagrange [Reference Lagrange19] showed that in
![]() $\kappa \mathsf {Bool}$
, all epimorphisms are regular. A consequence of his proof is the following key result, in some sense the main technical ingredient of this paper:
$\kappa \mathsf {Bool}$
, all epimorphisms are regular. A consequence of his proof is the following key result, in some sense the main technical ingredient of this paper:
Theorem 3.2 (Lagrange interpolation theorem)
Let

be a pushout in
![]() $\kappa \mathsf {Bool}$
. Then for any
$\kappa \mathsf {Bool}$
. Then for any
![]() $b \in B$
and
$b \in B$
and
![]() $c \in C$
such that
$c \in C$
such that
![]() $g'(b) \le f'(c)$
, there is
$g'(b) \le f'(c)$
, there is
![]() $a \in A$
such that
$a \in A$
such that
![]() $b \le f(a)$
and
$b \le f(a)$
and
![]() $g(a) \le c$
.
$g(a) \le c$
.
Proof Lagrange [Reference Lagrange19] proves that
![]() $\kappa \mathsf {Bool}$
has the (strong) amalgamation property, i.e., that if
$\kappa \mathsf {Bool}$
has the (strong) amalgamation property, i.e., that if
![]() $f, g$
above are injective, then so are
$f, g$
above are injective, then so are
![]() $f', g'$
(and the diagram is a pullback). While his argument can easily be adapted to yield the above statement, we can also deduce it abstractly, as follows. Let
$f', g'$
(and the diagram is a pullback). While his argument can easily be adapted to yield the above statement, we can also deduce it abstractly, as follows. Let
 $$ \begin{align*} U &:= \{a_1 \wedge \neg a_2 \mid b \le f(a_1) \mathrel{\,\&\,} g(a_2) \le c\} \subseteq A, \\ V &:= \{b_1 \wedge \neg f(a_2) \mid b \le b_1 \mathrel{\,\&\,} g(a_2) \le c\} \subseteq B, \\ W &:= \{g(a_1) \wedge \neg c_2 \mid b \le f(a_1) \mathrel{\,\&\,} c_2 \le c\} \subseteq C; \end{align*} $$
$$ \begin{align*} U &:= \{a_1 \wedge \neg a_2 \mid b \le f(a_1) \mathrel{\,\&\,} g(a_2) \le c\} \subseteq A, \\ V &:= \{b_1 \wedge \neg f(a_2) \mid b \le b_1 \mathrel{\,\&\,} g(a_2) \le c\} \subseteq B, \\ W &:= \{g(a_1) \wedge \neg c_2 \mid b \le f(a_1) \mathrel{\,\&\,} c_2 \le c\} \subseteq C; \end{align*} $$
these are
![]() $\kappa $
-filters. It is easily seen that
$\kappa $
-filters. It is easily seen that
![]() $U = f^{-1}(V) = g^{-1}(W)$
, whence replacing
$U = f^{-1}(V) = g^{-1}(W)$
, whence replacing
![]() $A, B, C$
with
$A, B, C$
with
![]() $A/U, B/V, C/W$
respectively in the diagram above renders
$A/U, B/V, C/W$
respectively in the diagram above renders
![]() $f, g$
injective. Clearly
$f, g$
injective. Clearly
![]() $b \in V$
and
$b \in V$
and
![]() $\neg c \in W$
, i.e.,
$\neg c \in W$
, i.e.,
![]() $b, c$
become
$b, c$
become
![]() $\top , \bot $
in
$\top , \bot $
in
![]() $B/V, C/W$
respectively; thus
$B/V, C/W$
respectively; thus
![]() $g'(b) \le f'(c) \in B \otimes _A C$
implies that
$g'(b) \le f'(c) \in B \otimes _A C$
implies that
![]() $B/V \otimes _{A/U} C/W$
is trivial. Now by amalgamation,
$B/V \otimes _{A/U} C/W$
is trivial. Now by amalgamation,
![]() $A/U$
must be trivial, i.e.,
$A/U$
must be trivial, i.e.,
![]() $\bot \in U$
, i.e., there are
$\bot \in U$
, i.e., there are
![]() $a_1 \le a_2 \in A$
such that
$a_1 \le a_2 \in A$
such that
![]() $b \le f(a_1)$
and
$b \le f(a_1)$
and
![]() $g(a_2) \le c$
. Taking
$g(a_2) \le c$
. Taking
![]() $a := a_1$
works.
$a := a_1$
works.
Corollary 3.3 (Lagrange)
All epimorphisms in
![]() $\kappa \mathsf {Bool}$
are surjective.
$\kappa \mathsf {Bool}$
are surjective.
Proof Let
![]() $f : A \to B \in \kappa \mathsf {Bool}$
be an epimorphism, i.e., the above diagram with
$f : A \to B \in \kappa \mathsf {Bool}$
be an epimorphism, i.e., the above diagram with
![]() $g = f$
,
$g = f$
,
![]() $C = B = B \otimes _A C$
, and
$C = B = B \otimes _A C$
, and
![]() $f' = g' = 1_B$
is a pushout. Then for any
$f' = g' = 1_B$
is a pushout. Then for any
![]() $b \in B$
, by Theorem 3.2, there is
$b \in B$
, by Theorem 3.2, there is
![]() $a \in A$
such that
$a \in A$
such that
![]() $b \le f(a) \le b$
.
$b \le f(a) \le b$
.
Corollary 3.4. For any
![]() $\kappa $
-presented
$\kappa $
-presented
![]() $\kappa $
-Boolean algebra A, we have an order-isomorphism
$\kappa $
-Boolean algebra A, we have an order-isomorphism
 $$ \begin{align*} A &\cong \mathrm{Sub}_{\kappa\mathsf{Bool}_{\kappa}^{\mathrm{op}}}(A) \\ a &\mapsto A/a \cong {\downarrow} a, \end{align*} $$
$$ \begin{align*} A &\cong \mathrm{Sub}_{\kappa\mathsf{Bool}_{\kappa}^{\mathrm{op}}}(A) \\ a &\mapsto A/a \cong {\downarrow} a, \end{align*} $$
which as A varies is a natural transformation
![]() $1_{\kappa \mathsf {Bool}_{\kappa }} \to \mathrm {Sub}_{\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}} : \kappa \mathsf {Bool}_{\kappa } \to \kappa \mathsf {Bool}_{\kappa }$
, i.e., a homomorphism
$1_{\kappa \mathsf {Bool}_{\kappa }} \to \mathrm {Sub}_{\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}} : \kappa \mathsf {Bool}_{\kappa } \to \kappa \mathsf {Bool}_{\kappa }$
, i.e., a homomorphism
![]() $f : A \to B \in \kappa \mathsf {Bool}_{\kappa }$
corresponds to pullback of subobjects
$f : A \to B \in \kappa \mathsf {Bool}_{\kappa }$
corresponds to pullback of subobjects
![]() $\mathrm {Sub}_{\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}}(A) \to \mathrm {Sub}_{\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}}(B)$
along
$\mathrm {Sub}_{\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}}(A) \to \mathrm {Sub}_{\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}}(B)$
along
![]() $f : B \to A \in \kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
.
$f : B \to A \in \kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
.
We will also need the following more technical consequence of Theorem 3.2:
Lemma 3.5. Let
![]() $Z \subseteq X$
be
$Z \subseteq X$
be
![]() $\kappa $
-ary sets, let
$\kappa $
-ary sets, let

be a pushout in
![]() $\mathsf {Set}_{\kappa }$
, where i is the inclusion, and consider the induced pushout
$\mathsf {Set}_{\kappa }$
, where i is the inclusion, and consider the induced pushout

in
![]() $\kappa \mathsf {Bool}_{\kappa }$
. For any
$\kappa \mathsf {Bool}_{\kappa }$
. For any
![]() $b \in \mathcal {K}(X)$
such that
$b \in \mathcal {K}(X)$
such that
there is a retraction
![]() $h : \mathcal {K}(X) \twoheadrightarrow \mathcal {K}(Z) \in \kappa \mathsf {Bool}_{\kappa }$
of
$h : \mathcal {K}(X) \twoheadrightarrow \mathcal {K}(Z) \in \kappa \mathsf {Bool}_{\kappa }$
of
![]() $i_* : \mathcal {K}(Z) \hookrightarrow \mathcal {K}(X)$
such that
$i_* : \mathcal {K}(Z) \hookrightarrow \mathcal {K}(X)$
such that
Proof On generators
![]() $z \in Z \subseteq X \subseteq \mathcal {K}(X)$
, we must put
$z \in Z \subseteq X \subseteq \mathcal {K}(X)$
, we must put
![]() $h(z) := z \in \mathcal {K}(Z)$
to guarantee that h is a retraction of
$h(z) := z \in \mathcal {K}(Z)$
to guarantee that h is a retraction of
![]() $i_*$
. For
$i_*$
. For
![]() $y \in X \setminus Z$
, by (
$y \in X \setminus Z$
, by (
![]() $*$
), we have
$*$
), we have
whence by Theorem 3.2 there is some
![]() $h(y) \in \mathcal {K}(Z)$
such that
$h(y) \in \mathcal {K}(Z)$
such that
This defines h on generators
![]() $X \subseteq \mathcal {K}(X)$
.
$X \subseteq \mathcal {K}(X)$
.
Note that (
![]() $\ddagger $
), which also trivially holds for
$\ddagger $
), which also trivially holds for
![]() $y \in Z$
, says precisely that the homomorphism
$y \in Z$
, says precisely that the homomorphism
![]() $i_* \circ h : \mathcal {K}(X) \to \mathcal {K}(X)$
becomes equal (on generators
$i_* \circ h : \mathcal {K}(X) \to \mathcal {K}(X)$
becomes equal (on generators
![]() $y \in X$
) to the identity after projecting to the quotient
$y \in X$
) to the identity after projecting to the quotient
![]() $\mathcal {K}(X)/b \cong {\downarrow } b$
. Thus, (
$\mathcal {K}(X)/b \cong {\downarrow } b$
. Thus, (
![]() $\ddagger $
) holds more generally for all
$\ddagger $
) holds more generally for all
![]() $y \in \mathcal {K}(X)$
.
$y \in \mathcal {K}(X)$
.
We now verify (
![]() $\dagger $
). For
$\dagger $
). For
![]() $\le $
:
$\le $
:
![]() $b \le i_*(h(b))$
follows from (
$b \le i_*(h(b))$
follows from (
![]() $\ddagger $
) by taking
$\ddagger $
) by taking
![]() $y := b$
, while
$y := b$
, while
![]() $b \le i_*(h(y)) \leftrightarrow y$
is a restatement of (
$b \le i_*(h(y)) \leftrightarrow y$
is a restatement of (
![]() $\ddagger $
). For
$\ddagger $
). For
![]() $\ge $
: the right-hand side is the projection of
$\ge $
: the right-hand side is the projection of
![]() $i_*(h(b))$
to the quotient
$i_*(h(b))$
to the quotient
![]() $\mathcal {K}(X)/\bigwedge\nolimits_{y \in X/Z} (i_*(h(y)) \leftrightarrow y) \cong {\downarrow } \bigwedge\nolimits_{y \in X/Z} (i_*(h(y)) \leftrightarrow y)$
identifying each
$\mathcal {K}(X)/\bigwedge\nolimits_{y \in X/Z} (i_*(h(y)) \leftrightarrow y) \cong {\downarrow } \bigwedge\nolimits_{y \in X/Z} (i_*(h(y)) \leftrightarrow y)$
identifying each
![]() $y \in X \setminus Z$
with
$y \in X \setminus Z$
with
![]() $i_*(h(y))$
; clearly
$i_*(h(y))$
; clearly
![]() $y \in Z$
is also identified with
$y \in Z$
is also identified with
![]() $i_*(h(y)) = y$
, whence again
$i_*(h(y)) = y$
, whence again
![]() $i_* \circ h$
becomes equal to the identity after projecting to this quotient, whence
$i_* \circ h$
becomes equal to the identity after projecting to this quotient, whence
Remark 3.6. When
![]() $\kappa = \omega _1$
, the above results (when all the algebras are countably presented) correspond, via Loomis–Sikorski duality as in the following section, to familiar results in descriptive set theory. In Theorem 3.2, taking
$\kappa = \omega _1$
, the above results (when all the algebras are countably presented) correspond, via Loomis–Sikorski duality as in the following section, to familiar results in descriptive set theory. In Theorem 3.2, taking
![]() $A, B, C$
to be the duals of standard Borel spaces
$A, B, C$
to be the duals of standard Borel spaces
![]() $X, Y, Z$
respectively and
$X, Y, Z$
respectively and
![]() $f, g$
to be the duals of Borel maps
$f, g$
to be the duals of Borel maps
![]() $p : Y \to X$
and
$p : Y \to X$
and
![]() $q : Z \to X$
, the result says that for any Borel sets
$q : Z \to X$
, the result says that for any Borel sets
![]() $b \subseteq Y$
and
$b \subseteq Y$
and
![]() $c \subseteq Z$
such that
$c \subseteq Z$
such that
![]() $b \times _X Z \subseteq Y \times _X c$
, i.e.,
$b \times _X Z \subseteq Y \times _X c$
, i.e.,
![]() $p(b) \cap q(\neg c) = \emptyset $
, there is a Borel set
$p(b) \cap q(\neg c) = \emptyset $
, there is a Borel set
![]() $a \subseteq X$
such that
$a \subseteq X$
such that
![]() $b \subseteq p^{-1}(a)$
and
$b \subseteq p^{-1}(a)$
and
![]() $q^{-1}(a) \subseteq c$
, i.e.,
$q^{-1}(a) \subseteq c$
, i.e.,
![]() $p(b) \subseteq a$
and
$p(b) \subseteq a$
and
![]() $q(\neg c) \cap a = \emptyset $
. This is the Lusin separation theorem for
$q(\neg c) \cap a = \emptyset $
. This is the Lusin separation theorem for
![]() $\boldsymbol {\Sigma }^1_1$
sets (see [Reference Kechris18, Theorem 14.7]).
$\boldsymbol {\Sigma }^1_1$
sets (see [Reference Kechris18, Theorem 14.7]).
Both Corollary 3.4 and Lemma 3.5 are dual versions of the Lusin–Suslin theorem on injective Borel images (see [Reference Kechris18, Theorem 15.1]). Corollary 3.4 says that for any injective Borel map
![]() $p : Y \to X$
(dual to an epimorphism
$p : Y \to X$
(dual to an epimorphism
![]() $A \to B \in \sigma \mathsf {Bool}_{\sigma }$
), there is a Borel set
$A \to B \in \sigma \mathsf {Bool}_{\sigma }$
), there is a Borel set
![]() $a \subseteq X$
such that p is an isomorphism between Y and the Borel subspace a (dual to the quotient
$a \subseteq X$
such that p is an isomorphism between Y and the Borel subspace a (dual to the quotient
![]() $A/a$
). Lemma 3.5 says that for any countable sets
$A/a$
). Lemma 3.5 says that for any countable sets
![]() $X = Y \sqcup Z$
and Borel set
$X = Y \sqcup Z$
and Borel set
![]() $b \subseteq 2^X \cong 2^Z \times 2^Y$
such that
$b \subseteq 2^X \cong 2^Z \times 2^Y$
such that
![]() $b \times _{2^Z} b \subseteq 2^X \times _{2^Z} 2^X \cong 2^Z \times 2^Y \times 2^Y$
is contained in the diagonal, i.e., the projection
$b \times _{2^Z} b \subseteq 2^X \times _{2^Z} 2^X \cong 2^Z \times 2^Y \times 2^Y$
is contained in the diagonal, i.e., the projection
![]() $2^Z \times 2^Y \twoheadrightarrow 2^Z$
restricted to b is injective, there is a Borel map
$2^Z \times 2^Y \twoheadrightarrow 2^Z$
restricted to b is injective, there is a Borel map
![]() $u : 2^Z \to 2^Y$
whose graph contains b. (In fact, both proofs, once unravelled, can be seen as dual versions of the proof of Lusin–Suslin given in [Reference Chen6]. See also [Reference Chen8, Remark 3.4.26].)
$u : 2^Z \to 2^Y$
whose graph contains b. (In fact, both proofs, once unravelled, can be seen as dual versions of the proof of Lusin–Suslin given in [Reference Chen6]. See also [Reference Chen8, Remark 3.4.26].)
In the rest of this section, we verify that
![]() $\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
is
$\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
is
![]() $\kappa $
-complete Boolean
$\kappa $
-complete Boolean
![]() $\kappa $
-extensive. Clearly
$\kappa $
-extensive. Clearly
![]() $\kappa \mathsf {Bool}_{\kappa } \subseteq \kappa \mathsf {Bool}$
is closed under
$\kappa \mathsf {Bool}_{\kappa } \subseteq \kappa \mathsf {Bool}$
is closed under
![]() $\kappa $
-ary colimits, whence
$\kappa $
-ary colimits, whence
![]() $\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
is
$\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
is
![]() $\kappa $
-complete. Booleanness follows from Corollary 3.4. Thus, it remains to show
$\kappa $
-complete. Booleanness follows from Corollary 3.4. Thus, it remains to show
![]() $\kappa $
-extensivity.Footnote
6
$\kappa $
-extensivity.Footnote
6
Proposition 3.7.
![]() $\kappa $
-ary products of
$\kappa $
-ary products of
![]() $\kappa $
-presented
$\kappa $
-presented
![]() $\kappa $
-Boolean algebras are
$\kappa $
-Boolean algebras are
![]() $\kappa $
-presented. Thus,
$\kappa $
-presented. Thus,
![]() $\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
has
$\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
has
![]() $\kappa $
-ary coproducts.
$\kappa $
-ary coproducts.
Proof It is standard that when
![]() ${<} \kappa $
-many elements
${<} \kappa $
-many elements
![]() $c_i \in A$
of a
$c_i \in A$
of a
![]() $\kappa $
-ary Boolean algebra A form a partition, i.e.,
$\kappa $
-ary Boolean algebra A form a partition, i.e.,
![]() $\bigvee _i c_i = \top $
and
$\bigvee _i c_i = \top $
and
![]() $c_i \wedge c_j = \bot $
for
$c_i \wedge c_j = \bot $
for
![]() $i \ne j$
, then we have an isomorphism
$i \ne j$
, then we have an isomorphism
 $$ \begin{align*} A &\cong \prod_i {\downarrow} c_i \cong \prod_i A/c_i \\ a &\mapsto (c_i \wedge a)_i. \end{align*} $$
$$ \begin{align*} A &\cong \prod_i {\downarrow} c_i \cong \prod_i A/c_i \\ a &\mapsto (c_i \wedge a)_i. \end{align*} $$
Now let
![]() $A_i = \mathcal {K}(X_i)/r_i$
with
$A_i = \mathcal {K}(X_i)/r_i$
with
![]() ${\lvert }X_i{\rvert } < \kappa $
and
${\lvert }X_i{\rvert } < \kappa $
and
![]() $r_i \in \mathcal {K}(X_i)$
for each
$r_i \in \mathcal {K}(X_i)$
for each
![]() $i \in I$
,
$i \in I$
,
![]() ${\lvert }{I}{\rvert } < \kappa $
, be
${\lvert }{I}{\rvert } < \kappa $
, be
![]() $\kappa $
-presented
$\kappa $
-presented
![]() $\kappa $
-Boolean algebras. Then we claim
$\kappa $
-Boolean algebras. Then we claim
 $$ \begin{align*} &\prod_i A_i \cong \mathcal{K}(I \sqcup \bigsqcup\nolimits_i X_i)/s \quad \text{where}\\ & \quad s := \bigwedge\nolimits_{i \ne j} \neg(i \wedge j) \wedge (\bigvee\nolimits_i i) \wedge \bigwedge\nolimits_i \bigwedge\nolimits_{x \in X_i} (x \to i) \wedge \bigwedge\nolimits_i (i \to r_i). \end{align*} $$
$$ \begin{align*} &\prod_i A_i \cong \mathcal{K}(I \sqcup \bigsqcup\nolimits_i X_i)/s \quad \text{where}\\ & \quad s := \bigwedge\nolimits_{i \ne j} \neg(i \wedge j) \wedge (\bigvee\nolimits_i i) \wedge \bigwedge\nolimits_i \bigwedge\nolimits_{x \in X_i} (x \to i) \wedge \bigwedge\nolimits_i (i \to r_i). \end{align*} $$
Indeed, the relations in s ensure that the generators
![]() $i \in I \subseteq \mathcal {K}(I \sqcup \bigsqcup\nolimits _j X_j)$
form a partition in
$i \in I \subseteq \mathcal {K}(I \sqcup \bigsqcup\nolimits _j X_j)$
form a partition in
![]() $\mathcal {K}(I \sqcup \bigsqcup\nolimits _j X_j)/s$
, and that for each
$\mathcal {K}(I \sqcup \bigsqcup\nolimits _j X_j)/s$
, and that for each
![]() $i \in I$
we have
$i \in I$
we have
 $$ \begin{align*} \mathcal{K}(I \sqcup \bigsqcup\nolimits_j X_j)/s/i &\cong \mathcal{K}(I \sqcup \bigsqcup\nolimits_j X_j)/(s \wedge i) \\ &= \mathcal{K}(I \sqcup \bigsqcup\nolimits_j X_j)/(i \wedge \bigwedge\nolimits_{j \ne i} (\neg j \wedge \bigwedge\nolimits_{x \in X_j} \neg x) \wedge r_i) \\ &\cong \mathcal{K}(X_i)/r_i = A_i. \end{align*} $$
$$ \begin{align*} \mathcal{K}(I \sqcup \bigsqcup\nolimits_j X_j)/s/i &\cong \mathcal{K}(I \sqcup \bigsqcup\nolimits_j X_j)/(s \wedge i) \\ &= \mathcal{K}(I \sqcup \bigsqcup\nolimits_j X_j)/(i \wedge \bigwedge\nolimits_{j \ne i} (\neg j \wedge \bigwedge\nolimits_{x \in X_j} \neg x) \wedge r_i) \\ &\cong \mathcal{K}(X_i)/r_i = A_i. \end{align*} $$
Proposition 3.8.
![]() $\kappa \mathsf {Bool}^{\mathrm {op}}$
and
$\kappa \mathsf {Bool}^{\mathrm {op}}$
and
![]() $\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
are
$\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
are
![]() $\kappa $
-extensive.
$\kappa $
-extensive.
Proof Clearly, product projections in
![]() $\kappa \mathsf {Bool}$
are surjective, and for a product
$\kappa \mathsf {Bool}$
are surjective, and for a product
![]() $\prod _k A_k$
and
$\prod _k A_k$
and
![]() $i \ne j$
, the pushout of the projections
$i \ne j$
, the pushout of the projections
![]() $\pi _i : \prod _k A_k \to A_i$
and
$\pi _i : \prod _k A_k \to A_i$
and
![]() $\pi _j : \prod _k A_k \to A_j$
is trivial, as witnessed by any
$\pi _j : \prod _k A_k \to A_j$
is trivial, as witnessed by any
![]() $\vec {a} \in \prod _k A_k$
with
$\vec {a} \in \prod _k A_k$
with
![]() $a_i = \bot $
and
$a_i = \bot $
and
![]() $a_j = \top $
. Thus,
$a_j = \top $
. Thus,
![]() $\kappa $
-ary coproducts in
$\kappa $
-ary coproducts in
![]() $\kappa \mathsf {Bool}^{\mathrm {op}}$
are disjoint.
$\kappa \mathsf {Bool}^{\mathrm {op}}$
are disjoint.
It remains to verify pullback-stability. Let
![]() $A_i \in \kappa \mathsf {Bool}$
for
$A_i \in \kappa \mathsf {Bool}$
for
![]() $i \in I$
,
$i \in I$
,
![]() ${\lvert }{I}{\rvert } < \kappa $
, and
${\lvert }{I}{\rvert } < \kappa $
, and
![]() $f : \prod _i A_i \to B \in \kappa \mathsf {Bool}$
, let
$f : \prod _i A_i \to B \in \kappa \mathsf {Bool}$
, let
![]() $\pi _i : \prod _k A_k \to A_i$
be the projections, and let
$\pi _i : \prod _k A_k \to A_i$
be the projections, and let

be pushouts; we must show that the
![]() $g_i$
exhibit B as the product
$g_i$
exhibit B as the product
For each
![]() $a \in A_i$
, let
$a \in A_i$
, let
![]() $\delta _i(a) \in \prod _k A_k$
be given by
$\delta _i(a) \in \prod _k A_k$
be given by
![]() $\delta _i(a)_i := a$
and
$\delta _i(a)_i := a$
and
![]() $\delta _i(a)_j := \bot $
for all
$\delta _i(a)_j := \bot $
for all
![]() $j \ne i$
. Then
$j \ne i$
. Then
![]() $(\delta _i(\top ))_i$
form a partition in
$(\delta _i(\top ))_i$
form a partition in
![]() $\prod _k A_k$
, whence
$\prod _k A_k$
, whence
![]() $(f(\delta _i(\top )))_i$
form a partition in B. Each
$(f(\delta _i(\top )))_i$
form a partition in B. Each
![]() $g_i(f(\delta _i(\top ))) = f_i(\pi _i(\delta _i(\top ))) = f_i(\top ) = \top $
, whence
$g_i(f(\delta _i(\top ))) = f_i(\pi _i(\delta _i(\top ))) = f_i(\top ) = \top $
, whence
![]() $g_i$
factors through
$g_i$
factors through
![]() $B/f(\delta _i(\top )) {\kern-1.2pt}\cong{\kern-1pt} {\downarrow } f(\delta _i(\top ))$
as the restriction
$B/f(\delta _i(\top )) {\kern-1.2pt}\cong{\kern-1pt} {\downarrow } f(\delta _i(\top ))$
as the restriction
![]() $g_i|{\downarrow } f(\delta _i(\top )){\kern-1.2pt} :{\kern-1.2pt} {\downarrow } f(\delta _i(\top )) {\kern-1.2pt}\to{\kern-1.2pt} A_i \otimes _{\prod _k A_k} B$
. So it is enough to show that each
$g_i|{\downarrow } f(\delta _i(\top )){\kern-1.2pt} :{\kern-1.2pt} {\downarrow } f(\delta _i(\top )) {\kern-1.2pt}\to{\kern-1.2pt} A_i \otimes _{\prod _k A_k} B$
. So it is enough to show that each
![]() $g_i|{\downarrow } f(\delta _i(\top ))$
is an isomorphism, since then g factors as
$g_i|{\downarrow } f(\delta _i(\top ))$
is an isomorphism, since then g factors as
![]() $B \cong \prod _i {\downarrow } f(\delta _i(\top )) \cong \prod _i (A_i \otimes _{\prod _k A_k} B)$
. We claim that
$B \cong \prod _i {\downarrow } f(\delta _i(\top )) \cong \prod _i (A_i \otimes _{\prod _k A_k} B)$
. We claim that
![]() $g_i|{\downarrow } f(\delta _i(\top ))$
has inverse defined via the universal property of the pushout by
$g_i|{\downarrow } f(\delta _i(\top ))$
has inverse defined via the universal property of the pushout by
 $$ \begin{align*} h_i : A_i \otimes_{\prod_k A_k} B &\longrightarrow {\downarrow} f(\delta_i(\top)) \\ f_i(a) &\longmapsto f(\delta_i(a)) \\ g_i(b) &\longmapsto f(\delta_i(\top)) \wedge b. \end{align*} $$
$$ \begin{align*} h_i : A_i \otimes_{\prod_k A_k} B &\longrightarrow {\downarrow} f(\delta_i(\top)) \\ f_i(a) &\longmapsto f(\delta_i(a)) \\ g_i(b) &\longmapsto f(\delta_i(\top)) \wedge b. \end{align*} $$
![]() $h_i$
is well-defined, since for
$h_i$
is well-defined, since for
![]() $\vec {a} \in \prod _k A_k$
we have
$\vec {a} \in \prod _k A_k$
we have
 $$ \begin{align*} h_i(f_i(\pi_i(\vec{a}))) &:= f(\delta_i(\pi_i(\vec{a}))) \\ &= f(\delta_i(a_i)) \\ &= f(\delta_i(\top) \wedge \vec{a}) \\ &= f(\delta_i(\top)) \wedge f(\vec{a}) =: h_i(g_i(f(\vec{a}))). \end{align*} $$
$$ \begin{align*} h_i(f_i(\pi_i(\vec{a}))) &:= f(\delta_i(\pi_i(\vec{a}))) \\ &= f(\delta_i(a_i)) \\ &= f(\delta_i(\top) \wedge \vec{a}) \\ &= f(\delta_i(\top)) \wedge f(\vec{a}) =: h_i(g_i(f(\vec{a}))). \end{align*} $$
For all
![]() $b \in {\downarrow } f(\delta _i(\top ))$
, we have
$b \in {\downarrow } f(\delta _i(\top ))$
, we have
![]() $h_i(g_i(b)) = f(\delta _i(\top )) \wedge b = b$
; thus
$h_i(g_i(b)) = f(\delta _i(\top )) \wedge b = b$
; thus
![]() $h_i \circ g_i|{\downarrow } f(\delta _i(\top )) = 1_{{\downarrow } f(\delta _i(\top ))}$
. For all generators
$h_i \circ g_i|{\downarrow } f(\delta _i(\top )) = 1_{{\downarrow } f(\delta _i(\top ))}$
. For all generators
![]() $f_i(a) \in A_i \otimes _{\prod _k A_k} B$
and
$f_i(a) \in A_i \otimes _{\prod _k A_k} B$
and
![]() $g_i(b) \in A_i \otimes _{\prod _k A_k} B$
, we have
$g_i(b) \in A_i \otimes _{\prod _k A_k} B$
, we have
 $$ \begin{align*} g_i(h_i(f_i(a))) &= g_i(f(\delta_i(a))) \\ &= f_i(\pi_i(\delta_i(a))) \\ &= f_i(a), \\ g_i(h_i(g_i(b))) &= g_i(f(\delta_i(\top)) \wedge b) \\ &= g_i(f(\delta_i(\top))) \wedge g_i(b) \\ &= f_i(\pi_i(\delta_i(\top))) \wedge g_i(b) \\ &= f_i(\top) \wedge g_i(b) \\ &= g_i(b); \end{align*} $$
$$ \begin{align*} g_i(h_i(f_i(a))) &= g_i(f(\delta_i(a))) \\ &= f_i(\pi_i(\delta_i(a))) \\ &= f_i(a), \\ g_i(h_i(g_i(b))) &= g_i(f(\delta_i(\top)) \wedge b) \\ &= g_i(f(\delta_i(\top))) \wedge g_i(b) \\ &= f_i(\pi_i(\delta_i(\top))) \wedge g_i(b) \\ &= f_i(\top) \wedge g_i(b) \\ &= g_i(b); \end{align*} $$
thus
![]() $g_i \circ h_i = 1_{A_i \otimes _{\prod _k A_k} B}$
.
$g_i \circ h_i = 1_{A_i \otimes _{\prod _k A_k} B}$
.
Corollary 3.9.
![]() $\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
is a
$\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
is a
![]() $\kappa $
-complete Boolean
$\kappa $
-complete Boolean
![]() $\kappa $
-extensive category.
$\kappa $
-extensive category.
4 Loomis–Sikorski duality
In this section, we review the Stone-type duality between standard Borel spaces and countably presented Boolean
![]() $\sigma $
-algebras. This duality is essentially a reformulation of the Loomis–Sikorski representation theorem for Boolean
$\sigma $
-algebras. This duality is essentially a reformulation of the Loomis–Sikorski representation theorem for Boolean
![]() $\sigma $
-algebras, of which we include a self-contained proof. This section is the only part of the paper that uses classical descriptive set theory (for which see [Reference Kechris18]).
$\sigma $
-algebras, of which we include a self-contained proof. This section is the only part of the paper that uses classical descriptive set theory (for which see [Reference Kechris18]).
An
![]() $\omega _1$
-Boolean algebra is conventionally called a Boolean
$\omega _1$
-Boolean algebra is conventionally called a Boolean
![]() $\sigma $
-algebra. In this context, we generally replace
$\sigma $
-algebra. In this context, we generally replace
![]() $\kappa $
with
$\kappa $
with
![]() $\sigma $
in the notation and terminology of the preceding section; for example, we have the category
$\sigma $
in the notation and terminology of the preceding section; for example, we have the category
![]() $\sigma \mathsf {Bool}_{\sigma } := \omega _1\mathsf {Bool}_{\omega _1}$
of countably presented Boolean
$\sigma \mathsf {Bool}_{\sigma } := \omega _1\mathsf {Bool}_{\omega _1}$
of countably presented Boolean
![]() $\sigma $
-algebras, the notion of
$\sigma $
-algebras, the notion of
![]() $\sigma $
-filter, etc.
$\sigma $
-filter, etc.
A Borel space (or measurable space) is a set X equipped with a (concrete)
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {B}(X)$
, i.e., a Boolean
$\mathcal {B}(X)$
, i.e., a Boolean
![]() $\sigma $
-subalgebra
$\sigma $
-subalgebra
![]() $\mathcal {B}(X) \subseteq \mathcal {P}(X)$
of the powerset, whose elements are called Borel sets in X. A Borel map (or measurable map)
$\mathcal {B}(X) \subseteq \mathcal {P}(X)$
of the powerset, whose elements are called Borel sets in X. A Borel map (or measurable map)
![]() $f : X \to Y$
between two Borel spaces is a map such that for every Borel set
$f : X \to Y$
between two Borel spaces is a map such that for every Borel set
![]() $B \in \mathcal {B}(Y)$
, the preimage
$B \in \mathcal {B}(Y)$
, the preimage
![]() $f^{-1}(B)$
is in
$f^{-1}(B)$
is in
![]() $\mathcal {B}(X)$
. Letting
$\mathcal {B}(X)$
. Letting
![]() $\mathsf {Bor}$
denote the category of Borel spaces and Borel maps, we thus have a functor
$\mathsf {Bor}$
denote the category of Borel spaces and Borel maps, we thus have a functor
![]() $\mathcal {B} : \mathsf {Bor}^{\mathrm {op}} \to \sigma \mathsf {Bool}$
, where
$\mathcal {B} : \mathsf {Bor}^{\mathrm {op}} \to \sigma \mathsf {Bool}$
, where
![]() $\mathcal {B}(f) := f^{-1} : \mathcal {B}(Y) \to \mathcal {B}(X)$
for a Borel map
$\mathcal {B}(f) := f^{-1} : \mathcal {B}(Y) \to \mathcal {B}(X)$
for a Borel map
![]() $f : X \to Y \in \mathsf {Bor}$
.
$f : X \to Y \in \mathsf {Bor}$
.
For an arbitrary Boolean
![]() $\sigma $
-algebra A, let
$\sigma $
-algebra A, let
![]() $\mathcal {S}_{\sigma }(A)$
denote the set of
$\mathcal {S}_{\sigma }(A)$
denote the set of
![]() $\sigma $
-ultrafilters on A, i.e.,
$\sigma $
-ultrafilters on A, i.e.,
![]() $\sigma $
-filters
$\sigma $
-filters
![]() $U \subseteq A$
whose complements are
$U \subseteq A$
whose complements are
![]() $\sigma $
-ideals. These are equivalently the preimages of
$\sigma $
-ideals. These are equivalently the preimages of
![]() $\top \in 2$
under (
$\top \in 2$
under (
![]() $\sigma $
-)homomorphisms
$\sigma $
-)homomorphisms
![]() $A \to 2$
. We equip
$A \to 2$
. We equip
![]() $\mathcal {S}_{\sigma }(A)$
with the Borel
$\mathcal {S}_{\sigma }(A)$
with the Borel
![]() $\sigma $
-algebra consisting of the sets
$\sigma $
-algebra consisting of the sets
for all
![]() $a \in A$
. In other words, the map
$a \in A$
. In other words, the map
![]() $[-] : A \to \mathcal {P}(\mathcal {S}_{\sigma }(A))$
is easily seen to be a
$[-] : A \to \mathcal {P}(\mathcal {S}_{\sigma }(A))$
is easily seen to be a
![]() $\sigma $
-homomorphism;
$\sigma $
-homomorphism;
![]() $\mathcal {B}(\mathcal {S}_{\sigma }(A))$
is by definition its image. For a homomorphism
$\mathcal {B}(\mathcal {S}_{\sigma }(A))$
is by definition its image. For a homomorphism
![]() $f : A \to B \in \sigma \mathsf {Bool}$
, taking preimage under f takes
$f : A \to B \in \sigma \mathsf {Bool}$
, taking preimage under f takes
![]() $\sigma $
-ultrafilters on B to
$\sigma $
-ultrafilters on B to
![]() $\sigma $
-ultrafilters on A, yielding a map
$\sigma $
-ultrafilters on A, yielding a map
![]() $\mathcal {S}_{\sigma }(f) := f^{-1} : \mathcal {S}_{\sigma }(B) \to \mathcal {S}_{\sigma }(A)$
; we have
$\mathcal {S}_{\sigma }(f) := f^{-1} : \mathcal {S}_{\sigma }(B) \to \mathcal {S}_{\sigma }(A)$
; we have
![]() $\mathcal {S}_{\sigma }(f)^{-1}([a]) = [f(a)]$
, whence
$\mathcal {S}_{\sigma }(f)^{-1}([a]) = [f(a)]$
, whence
![]() $\mathcal {S}_{\sigma }(f)$
is a Borel map. We thus have a functor
$\mathcal {S}_{\sigma }(f)$
is a Borel map. We thus have a functor
![]() $\mathcal {S}_{\sigma } : \sigma \mathsf {Bool}^{\mathrm {op}} \to \mathsf {Bor}$
.
$\mathcal {S}_{\sigma } : \sigma \mathsf {Bool}^{\mathrm {op}} \to \mathsf {Bor}$
.
The preceding two paragraphs are part of the general setup of a Stone-type duality between the categories
![]() $\sigma \mathsf {Bool}$
and
$\sigma \mathsf {Bool}$
and
![]() $\mathsf {Bor}$
, induced by the Borel structure and Boolean
$\mathsf {Bor}$
, induced by the Borel structure and Boolean
![]() $\sigma $
-algebra structure on the set
$\sigma $
-algebra structure on the set
![]() $2$
which “commute” with each other (see [Reference Johnstone16, VI Section 4] for the general theory of such dualities). For an arbitrary Boolean
$2$
which “commute” with each other (see [Reference Johnstone16, VI Section 4] for the general theory of such dualities). For an arbitrary Boolean
![]() $\sigma $
-algebra A and Borel space X, a Boolean
$\sigma $
-algebra A and Borel space X, a Boolean
![]() $\sigma $
-homomorphism
$\sigma $
-homomorphism
![]() $f : A \to \mathcal {B}(X)$
is determined by the set
$f : A \to \mathcal {B}(X)$
is determined by the set
which is required to have vertical fibers which are Borel subsets of X and horizontal fibers which are
![]() $\sigma $
-ultrafilters on A, which are the same conditions on the set
$\sigma $
-ultrafilters on A, which are the same conditions on the set
determining a Borel map
![]() $g : X \to \mathcal {S}_{\sigma }(A)$
. Thus we have a bijection
$g : X \to \mathcal {S}_{\sigma }(A)$
. Thus we have a bijection

which is easily seen to be natural in
![]() $A, X$
, yielding a contravariant adjunction between the functors
$A, X$
, yielding a contravariant adjunction between the functors
![]() $\mathcal {B} : \mathsf {Bor}^{\mathrm {op}} \to \sigma \mathsf {Bool}$
and
$\mathcal {B} : \mathsf {Bor}^{\mathrm {op}} \to \sigma \mathsf {Bool}$
and
![]() $\mathcal {S}_{\sigma } : \sigma \mathsf {Bool}^{\mathrm {op}} \to \mathsf {Bor}$
.
$\mathcal {S}_{\sigma } : \sigma \mathsf {Bool}^{\mathrm {op}} \to \mathsf {Bor}$
.
The adjunction unit on the
![]() $\mathsf {Bor}$
side consists of the Borel maps
$\mathsf {Bor}$
side consists of the Borel maps
 $$ \begin{align*} \eta_X : X &\longrightarrow \mathcal{S}_{\sigma}(\mathcal{B}(X)) = \{\sigma\text{-ultrafilters of Borel sets on } X\} \\ x &\longmapsto \{B \in \mathcal{B}(X) \mid x \in B\} \end{align*} $$
$$ \begin{align*} \eta_X : X &\longrightarrow \mathcal{S}_{\sigma}(\mathcal{B}(X)) = \{\sigma\text{-ultrafilters of Borel sets on } X\} \\ x &\longmapsto \{B \in \mathcal{B}(X) \mid x \in B\} \end{align*} $$
for each Borel space X, taking points to principal ultrafilters;
![]() $\eta _X$
is neither injective nor surjective in general.Footnote
7
On the
$\eta _X$
is neither injective nor surjective in general.Footnote
7
On the
![]() $\sigma \mathsf {Bool}$
side, the unit consists of the homomorphisms from above
$\sigma \mathsf {Bool}$
side, the unit consists of the homomorphisms from above
for each
![]() $A \in \sigma \mathsf {Bool}$
.
$A \in \sigma \mathsf {Bool}$
.
![]() $[-]_A$
is surjective by definition, and injective iff A admits enough
$[-]_A$
is surjective by definition, and injective iff A admits enough
![]() $\sigma $
-ultrafilters to separate points, or equivalently (by considering implications
$\sigma $
-ultrafilters to separate points, or equivalently (by considering implications
![]() $a \to b$
) every
$a \to b$
) every
![]() $a < \top \in A$
is outside of some
$a < \top \in A$
is outside of some
![]() $\sigma $
-ultrafilter; such A are precisely (isomorphic copies of) the concrete
$\sigma $
-ultrafilter; such A are precisely (isomorphic copies of) the concrete
![]() $\sigma $
-algebras of sets, i.e.,
$\sigma $
-algebras of sets, i.e.,
![]() $\mathcal {B}(X)$
for
$\mathcal {B}(X)$
for
![]() $X \in \mathsf {Bor}$
. In other words, the adjunction between
$X \in \mathsf {Bor}$
. In other words, the adjunction between
![]() $\mathcal {B}, \mathcal {S}_{\sigma }$
is idempotent (see, e.g., [Reference Johnstone16, VI Proposition 4.5]), and hence restricts to an adjoint equivalence
$\mathcal {B}, \mathcal {S}_{\sigma }$
is idempotent (see, e.g., [Reference Johnstone16, VI Proposition 4.5]), and hence restricts to an adjoint equivalence
between the full subcategories
![]() $\sigma \mathsf {Alg} \subseteq \sigma \mathsf {Bool}$
of (isomorphic copies of) concrete
$\sigma \mathsf {Alg} \subseteq \sigma \mathsf {Bool}$
of (isomorphic copies of) concrete
![]() $\sigma $
-algebras, and
$\sigma $
-algebras, and
![]() $\mathsf {Bor}' \subseteq \mathsf {Bor}$
of Borel spaces X such that
$\mathsf {Bor}' \subseteq \mathsf {Bor}$
of Borel spaces X such that
![]() $\eta _X$
is an isomorphism.
$\eta _X$
is an isomorphism.
The classical Loomis–Sikorski representation theorem (see, e.g., [Reference Sikorski27, 29.1]) states that every Boolean
![]() $\sigma $
-algebra is a quotient of a concrete
$\sigma $
-algebra is a quotient of a concrete
![]() $\sigma $
-algebra. By standard universal algebra,Footnote
8
this is equivalent to the following formulation, which is more relevant for our purposes. We include a self-contained proof for the reader’s convenience.Footnote
9
$\sigma $
-algebra. By standard universal algebra,Footnote
8
this is equivalent to the following formulation, which is more relevant for our purposes. We include a self-contained proof for the reader’s convenience.Footnote
9
Theorem 4.1 (Loomis–Sikorski)
![]() $\sigma \mathsf {Bool}_{\sigma } \subseteq \sigma \mathsf {Alg}$
, i.e., every countably presented Boolean
$\sigma \mathsf {Bool}_{\sigma } \subseteq \sigma \mathsf {Alg}$
, i.e., every countably presented Boolean
![]() $\sigma $
-algebra admits enough
$\sigma $
-algebra admits enough
![]() $\sigma $
-ultrafilters to separate points.
$\sigma $
-ultrafilters to separate points.
Proof Let
![]() $\mathcal {K}(X)/r \cong {\downarrow } r \in \sigma \mathsf {Bool}_{\sigma }$
, with X countable and
$\mathcal {K}(X)/r \cong {\downarrow } r \in \sigma \mathsf {Bool}_{\sigma }$
, with X countable and
![]() $r \in \mathcal {K}(X)$
. Let
$r \in \mathcal {K}(X)$
. Let
![]() $a \in {\downarrow } r$
with
$a \in {\downarrow } r$
with
![]() $a < \top _{{\downarrow } r} = r$
; we must find a
$a < \top _{{\downarrow } r} = r$
; we must find a
![]() $\sigma $
-ultrafilter
$\sigma $
-ultrafilter
![]() $U \subseteq {\downarrow } r$
not containing a. Since
$U \subseteq {\downarrow } r$
not containing a. Since
![]() $a < r$
,
$a < r$
,
![]() $r \to a < \top $
; so it is enough to find
$r \to a < \top $
; so it is enough to find
![]() $U \in \mathcal {S}_{\sigma }(\mathcal {K}(X))$
not containing
$U \in \mathcal {S}_{\sigma }(\mathcal {K}(X))$
not containing
![]() $r \to a$
, since then
$r \to a$
, since then
![]() $U \cap {\downarrow } r \in \mathcal {S}_{\sigma }({\downarrow } r)$
not containing a. So we may assume to begin with that
$U \cap {\downarrow } r \in \mathcal {S}_{\sigma }({\downarrow } r)$
not containing a. So we may assume to begin with that
![]() $r = \top $
and
$r = \top $
and
![]() $a < \top _{\mathcal {K}(X)}$
, and find
$a < \top _{\mathcal {K}(X)}$
, and find
![]() $U \in \mathcal {S}_{\sigma }(\mathcal {K}(X))$
not containing a.
$U \in \mathcal {S}_{\sigma }(\mathcal {K}(X))$
not containing a.
Let s be a Boolean
![]() $\sigma $
-algebra term (i.e., expression built from
$\sigma $
-algebra term (i.e., expression built from
![]() $\bigwedge , \bigvee , \neg , \top , \bot $
) in X evaluating to
$\bigwedge , \bigvee , \neg , \top , \bot $
) in X evaluating to
![]() $a \in \mathcal {K}(X)$
; for convenience, we regard
$a \in \mathcal {K}(X)$
; for convenience, we regard
![]() $\bigwedge $
as an abbreviation for
$\bigwedge $
as an abbreviation for
![]() $\neg \bigvee \neg $
. Let T be a countable set of Boolean
$\neg \bigvee \neg $
. Let T be a countable set of Boolean
![]() $\sigma $
-algebra terms containing s and each
$\sigma $
-algebra terms containing s and each
![]() $x \in X$
and closed under finite Boolean combinations (again without
$x \in X$
and closed under finite Boolean combinations (again without
![]() $\wedge $
) and subterms. For a term t, we let
$\wedge $
) and subterms. For a term t, we let
![]() ${\lfloor }{t}{\rfloor } \in \mathcal {K}(X)$
be its evaluation in
${\lfloor }{t}{\rfloor } \in \mathcal {K}(X)$
be its evaluation in
![]() $\mathcal {K}(X)$
. Then
$\mathcal {K}(X)$
. Then
![]() ${\lfloor }{T}{\rfloor } := \{{\lfloor }{t}{\rfloor } \mid t \in T\} \subseteq \mathcal {K}(X)$
is a countable (
${\lfloor }{T}{\rfloor } := \{{\lfloor }{t}{\rfloor } \mid t \in T\} \subseteq \mathcal {K}(X)$
is a countable (
![]() $\omega $
-)Boolean subalgebra containing a and the generators X. Each
$\omega $
-)Boolean subalgebra containing a and the generators X. Each
![]() $\sigma $
-ultrafilter
$\sigma $
-ultrafilter
![]() $U \subseteq \mathcal {K}(X)$
restricts to an (
$U \subseteq \mathcal {K}(X)$
restricts to an (
![]() $\omega $
-)ultrafilter
$\omega $
-)ultrafilter
![]() $U \cap {\lfloor }{T}{\rfloor } \subseteq {\lfloor }{T}{\rfloor }$
, which determines U since
$U \cap {\lfloor }{T}{\rfloor } \subseteq {\lfloor }{T}{\rfloor }$
, which determines U since
![]() $X \subseteq {\lfloor }{T}{\rfloor }$
; conversely, it is easy to show by induction on terms
$X \subseteq {\lfloor }{T}{\rfloor }$
; conversely, it is easy to show by induction on terms
![]() $t \in T$
that an arbitrary (
$t \in T$
that an arbitrary (
![]() $\omega $
-)ultrafilter
$\omega $
-)ultrafilter
![]() $V \subseteq {\lfloor }{T}{\rfloor }$
is the restriction of some
$V \subseteq {\lfloor }{T}{\rfloor }$
is the restriction of some
![]() $\sigma $
-ultrafilter
$\sigma $
-ultrafilter
![]() $U \subseteq \mathcal {K}(X)$
(namely, the unique U with the same restriction as V to X) iff
$U \subseteq \mathcal {K}(X)$
(namely, the unique U with the same restriction as V to X) iff
-
(*) for every
 $t = \bigvee _i t_i \in T$
, if
$t = \bigvee _i t_i \in T$
, if
 ${\lfloor }{t}{\rfloor } \in V$
, then
${\lfloor }{t}{\rfloor } \in V$
, then
 ${\lfloor }{t_i}{\rfloor } \in V$
for some i.
${\lfloor }{t_i}{\rfloor } \in V$
for some i.
By Baire category, the set of all such ultrafilters
![]() $V \subseteq {\lfloor }{T}{\rfloor }$
is a dense
$V \subseteq {\lfloor }{T}{\rfloor }$
is a dense
![]() $G_{\delta }$
in the Stone space
$G_{\delta }$
in the Stone space
![]() $\mathcal {S}_{\omega }({\lfloor }{T}{\rfloor })$
of
$\mathcal {S}_{\omega }({\lfloor }{T}{\rfloor })$
of
![]() ${\lfloor }{T}{\rfloor }$
(i.e., the compact Polish space of all ultrafilters on
${\lfloor }{T}{\rfloor }$
(i.e., the compact Polish space of all ultrafilters on
![]() ${\lfloor }{T}{\rfloor }$
), since for each
${\lfloor }{T}{\rfloor }$
), since for each
![]() $t = \bigvee _i t_i$
as in (
$t = \bigvee _i t_i$
as in (
![]() $*$
), the basic clopen set
$*$
), the basic clopen set
![]() $[{\lfloor }{t}{\rfloor }] := \{V \in \mathcal {S}_{\omega }({\lfloor }{T}{\rfloor }) \mid {\lfloor }{t}{\rfloor } \in V\}$
is the closure of
$[{\lfloor }{t}{\rfloor }] := \{V \in \mathcal {S}_{\omega }({\lfloor }{T}{\rfloor }) \mid {\lfloor }{t}{\rfloor } \in V\}$
is the closure of
![]() $\bigcup\nolimits_i [{\lfloor }{t_i}{\rfloor }]$
(whence the set of V obeying (
$\bigcup\nolimits_i [{\lfloor }{t_i}{\rfloor }]$
(whence the set of V obeying (
![]() $*$
) for that t is a dense open set
$*$
) for that t is a dense open set
![]() $\neg [{\lfloor }{t}{\rfloor }] \cup \bigcup\nolimits _i [{\lfloor }{t_i}{\rfloor }]$
). Since
$\neg [{\lfloor }{t}{\rfloor }] \cup \bigcup\nolimits _i [{\lfloor }{t_i}{\rfloor }]$
). Since
![]() $\top> a \in {\lfloor }{T}{\rfloor }$
,
$\top> a \in {\lfloor }{T}{\rfloor }$
,
![]() $\neg [a] \subseteq \mathcal {S}_{\omega }({\lfloor }{T}{\rfloor })$
is nonempty clopen, and hence contains some V satisfying (
$\neg [a] \subseteq \mathcal {S}_{\omega }({\lfloor }{T}{\rfloor })$
is nonempty clopen, and hence contains some V satisfying (
![]() $*$
), which extends to
$*$
), which extends to
![]() $U \in \mathcal {S}_{\sigma }(\mathcal {K}(X))$
not containing a.
$U \in \mathcal {S}_{\sigma }(\mathcal {K}(X))$
not containing a.
Hence, the above equivalence
![]() $\sigma \mathsf {Alg}^{\mathrm {op}} \cong \mathsf {Bor}'$
restricts to an equivalence between
$\sigma \mathsf {Alg}^{\mathrm {op}} \cong \mathsf {Bor}'$
restricts to an equivalence between
![]() $\sigma \mathsf {Bool}_{\sigma }^{\mathrm {op}}$
and the full subcategory of
$\sigma \mathsf {Bool}_{\sigma }^{\mathrm {op}}$
and the full subcategory of
![]() $\mathsf {Bor}$
consisting of those Borel spaces (isomorphic to ones) of the form
$\mathsf {Bor}$
consisting of those Borel spaces (isomorphic to ones) of the form
![]() $\mathcal {S}_{\sigma }(A)$
for some countably presented Boolean
$\mathcal {S}_{\sigma }(A)$
for some countably presented Boolean
![]() $\sigma $
-algebra A. For a free algebra
$\sigma $
-algebra A. For a free algebra
![]() $\mathcal {K}(X)$
, X countable,
$\mathcal {K}(X)$
, X countable,
![]() $\sigma $
-ultrafilters
$\sigma $
-ultrafilters
![]() $U \in \mathcal {S}_{\sigma }(\mathcal {K}(X))$
are determined by their restrictions to X, i.e.,
$U \in \mathcal {S}_{\sigma }(\mathcal {K}(X))$
are determined by their restrictions to X, i.e.,
![]() $\mathcal {S}_{\sigma }(\mathcal {K}(X)) \cong 2^X$
, with Borel
$\mathcal {S}_{\sigma }(\mathcal {K}(X)) \cong 2^X$
, with Borel
![]() $\sigma $
-algebra generated by the subbasic Borel sets
$\sigma $
-algebra generated by the subbasic Borel sets
![]() $[x] := \{U \in 2^X \mid x \in U\}$
for
$[x] := \{U \in 2^X \mid x \in U\}$
for
![]() $x \in X$
, i.e., the standard Borel
$x \in X$
, i.e., the standard Borel
![]() $\sigma $
-algebra induced by the product topology. Passing to a countably presented quotient
$\sigma $
-algebra induced by the product topology. Passing to a countably presented quotient
![]() $\mathcal {K}(X)/r \cong {\downarrow } r$
amounts to restricting to a Borel subspace
$\mathcal {K}(X)/r \cong {\downarrow } r$
amounts to restricting to a Borel subspace
![]() $[r] \subseteq 2^X$
. Thus the spaces
$[r] \subseteq 2^X$
. Thus the spaces
![]() $\mathcal {S}_{\sigma }(A)$
for
$\mathcal {S}_{\sigma }(A)$
for
![]() $A \in \sigma \mathsf {Bool}_{\sigma }$
are exactly the standard Borel spaces (isomorphic copies of Borel subspaces of Cantor space
$A \in \sigma \mathsf {Bool}_{\sigma }$
are exactly the standard Borel spaces (isomorphic copies of Borel subspaces of Cantor space
![]() $2^{\mathbb {N}}$
). Letting
$2^{\mathbb {N}}$
). Letting
![]() $\mathsf {SBor} \subseteq \mathsf {Bor}$
denote the full subcategory of standard Borel spaces, we have
$\mathsf {SBor} \subseteq \mathsf {Bor}$
denote the full subcategory of standard Borel spaces, we have
Corollary 4.2 (Loomis–Sikorski duality)
The functors
![]() $\mathcal {B}, \mathcal {S}_{\sigma }$
restrict to an adjoint equivalence
$\mathcal {B}, \mathcal {S}_{\sigma }$
restrict to an adjoint equivalence
This reduces Theorem 1.1 to Theorem 1.2 for
![]() $\kappa = \omega _1$
.
$\kappa = \omega _1$
.
5 Almost universal
 $\mathcal {L}_{\kappa \kappa }$
-theories
$\mathcal {L}_{\kappa \kappa }$
-theories
In this section, we introduce the infinitary first-order logic whose theories present
![]() $\kappa $
-complete Boolean subextensive categories via the standard “syntactic category” construction from categorical logic. See [Reference Makkai and Reyes23] and [Reference Johnstone17, Chapter D1] for general background on categorical logic and syntactic categories (also [Reference Chen7] for a treatment of the logic
$\kappa $
-complete Boolean subextensive categories via the standard “syntactic category” construction from categorical logic. See [Reference Makkai and Reyes23] and [Reference Johnstone17, Chapter D1] for general background on categorical logic and syntactic categories (also [Reference Chen7] for a treatment of the logic
![]() $\mathcal {L}_{\omega _1\omega }$
similar to that given here). We then give a presentation of
$\mathcal {L}_{\omega _1\omega }$
similar to that given here). We then give a presentation of
![]() $\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
via such a theory, thereby characterizing
$\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
via such a theory, thereby characterizing
![]() $\kappa $
-continuous extensive functors
$\kappa $
-continuous extensive functors
![]() $\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}} \to \mathsf {C}$
for arbitrary
$\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}} \to \mathsf {C}$
for arbitrary
![]() $\mathsf {C} \in \kappa \mathfrak {LimBSExtCat}$
, which we use to prove Theorem 1.2.
$\mathsf {C} \in \kappa \mathfrak {LimBSExtCat}$
, which we use to prove Theorem 1.2.
The logic in question is the fragment of the full
![]() $\kappa $
-ary first order logic
$\kappa $
-ary first order logic
![]() $\mathcal {L}_{\kappa \kappa }$
consisting of formulas which do not contain
$\mathcal {L}_{\kappa \kappa }$
consisting of formulas which do not contain
![]() $\forall $
and only contain
$\forall $
and only contain
![]() $\exists $
when the existential is already provably unique relative to the background theory. We call such formulas almost quantifier-free, and the corresponding theories (inductively built from sentences which are universally quantified almost quantifier-free formulas relative to the predecessor theory) almost universal. This “provably unique
$\exists $
when the existential is already provably unique relative to the background theory. We call such formulas almost quantifier-free, and the corresponding theories (inductively built from sentences which are universally quantified almost quantifier-free formulas relative to the predecessor theory) almost universal. This “provably unique
![]() $\exists $
” is well-known in categorical logic as an essential part of finite-limit logic or Cartesian logic, the fragment of finitary first-order logic
$\exists $
” is well-known in categorical logic as an essential part of finite-limit logic or Cartesian logic, the fragment of finitary first-order logic
![]() $\mathcal {L}_{\omega \omega }$
(due to Coste [Reference Coste, Fourman, Mulvey and Scott10]; see also [Reference Johnstone17, Definition D1.3.4]) used to present finitely complete categories. The combination with arbitrary quantifier-free Boolean formulas seems to be new (although it contains Johnstone’s [Reference Johnstone, Fourman, Mulvey and Scott15] disjunctive logic, used to present extensive categories without Booleanness). Because of this, and because of the somewhat delicate inductions involving the “provably unique
$\mathcal {L}_{\omega \omega }$
(due to Coste [Reference Coste, Fourman, Mulvey and Scott10]; see also [Reference Johnstone17, Definition D1.3.4]) used to present finitely complete categories. The combination with arbitrary quantifier-free Boolean formulas seems to be new (although it contains Johnstone’s [Reference Johnstone, Fourman, Mulvey and Scott15] disjunctive logic, used to present extensive categories without Booleanness). Because of this, and because of the somewhat delicate inductions involving the “provably unique
![]() $\exists $
” which may not be well-known outside categorical logic, we will develop the syntactic category in some detail, even though all the ideas involved are essentially standard.
$\exists $
” which may not be well-known outside categorical logic, we will develop the syntactic category in some detail, even though all the ideas involved are essentially standard.
5.1 Formulas and theories
Recall from Section 2 our standing assumption that
![]() $\mathsf {Set}^{\prime }_{\kappa }$
is the full subcategory of
$\mathsf {Set}^{\prime }_{\kappa }$
is the full subcategory of
![]() $\mathsf {Set}$
consisting of all
$\mathsf {Set}$
consisting of all
![]() $\kappa $
-ary subsets of a fixed set
$\kappa $
-ary subsets of a fixed set
![]() $\mathbb {U}$
of size
$\mathbb {U}$
of size
![]() $\ge \kappa $
.
$\ge \kappa $
.
Let
![]() $\mathcal {L}$
be a (single-sorted)
Footnote
10
$\mathcal {L}$
be a (single-sorted)
Footnote
10
![]() $\kappa $
-ary first-order relational language, consisting of, for each
$\kappa $
-ary first-order relational language, consisting of, for each
![]() $X \in \mathsf {Set}^{\prime }_{\kappa }$
, a set
$X \in \mathsf {Set}^{\prime }_{\kappa }$
, a set
![]() $\mathcal {L}(X)$
of X-ary relation symbols.Footnote
11
$\mathcal {L}(X)$
of X-ary relation symbols.Footnote
11
The
![]() $\mathcal {L}_{\kappa \kappa }$
-formulas are defined inductively as follows. The variables of formulas will be elements of the sets
$\mathcal {L}_{\kappa \kappa }$
-formulas are defined inductively as follows. The variables of formulas will be elements of the sets
![]() $X \in \mathsf {Set}^{\prime }_{\kappa }$
; we only consider formulas whose free variables all belong to some
$X \in \mathsf {Set}^{\prime }_{\kappa }$
; we only consider formulas whose free variables all belong to some
![]() $X \in \mathsf {Set}^{\prime }_{\kappa }$
. We will keep track of free variables of formulas; for
$X \in \mathsf {Set}^{\prime }_{\kappa }$
. We will keep track of free variables of formulas; for
![]() $X \in \mathsf {Set}^{\prime }_{\kappa }$
, we write
$X \in \mathsf {Set}^{\prime }_{\kappa }$
, we write
![]() $\mathcal {L}_{\kappa \kappa }(X)$
for the set of
$\mathcal {L}_{\kappa \kappa }(X)$
for the set of
![]() $\mathcal {L}_{\kappa \kappa }$
-formulas
$\mathcal {L}_{\kappa \kappa }$
-formulas
![]() $\phi $
with free variables from X (X is called the context of
$\phi $
with free variables from X (X is called the context of
![]() $\phi $
).
$\phi $
).
-
• For
 $X \in \mathsf {Set}^{\prime }_{\kappa }$
, a Y-ary tuple of variables
$X \in \mathsf {Set}^{\prime }_{\kappa }$
, a Y-ary tuple of variables
 $\vec {x} \in X^Y$
where
$\vec {x} \in X^Y$
where
 $Y \in \mathsf {Set}^{\prime }_{\kappa }$
, and a Y-ary relational symbol
$Y \in \mathsf {Set}^{\prime }_{\kappa }$
, and a Y-ary relational symbol
 $R \in \mathcal {L}(Y)$
, we have an atomic formula
$R \in \mathcal {L}(Y)$
, we have an atomic formula
 $R(\vec {x}) \in \mathcal {L}_{\kappa \kappa }(X)$
.
$R(\vec {x}) \in \mathcal {L}_{\kappa \kappa }(X)$
. -
• For
 $X \in \mathsf {Set}^{\prime }_{\kappa }$
and
$X \in \mathsf {Set}^{\prime }_{\kappa }$
and
 $x, y \in X$
, we have an atomic formula
$x, y \in X$
, we have an atomic formula
 $(x = y) \in \mathcal {L}_{\kappa \kappa }(X)$
.
$(x = y) \in \mathcal {L}_{\kappa \kappa }(X)$
. -
• For
 $X, I \in \mathsf {Set}^{\prime }_{\kappa }$
and
$X, I \in \mathsf {Set}^{\prime }_{\kappa }$
and
 $\phi , \phi _i \in \mathcal {L}_{\kappa \kappa }(X)$
for each
$\phi , \phi _i \in \mathcal {L}_{\kappa \kappa }(X)$
for each
 $i \in I$
, we have
$i \in I$
, we have
 $\neg \phi , \bigvee _{i \in I} \phi _i, \bigwedge _{i \in I} \phi _i \in \mathcal {L}_{\kappa \kappa }(X)$
(when
$\neg \phi , \bigvee _{i \in I} \phi _i, \bigwedge _{i \in I} \phi _i \in \mathcal {L}_{\kappa \kappa }(X)$
(when
 $I = \emptyset $
, we write
$I = \emptyset $
, we write
 $\bot := \bigvee _{i \in \emptyset } \phi _i$
and
$\bot := \bigvee _{i \in \emptyset } \phi _i$
and
 $\top := \bigwedge\nolimits_{i \in \emptyset } \phi _i$
; when
$\top := \bigwedge\nolimits_{i \in \emptyset } \phi _i$
; when
 $I = n \in \mathbb {N}$
, we write
$I = n \in \mathbb {N}$
, we write
 $\phi _0 \vee \dotsb \vee \phi _{n-1} := \bigvee _{i \in n} \phi _i$
, and similarly for
$\phi _0 \vee \dotsb \vee \phi _{n-1} := \bigvee _{i \in n} \phi _i$
, and similarly for
 $\wedge $
).
$\wedge $
). -
• For
 $X \in \mathsf {Set}^{\prime }_{\kappa }$
,
$X \in \mathsf {Set}^{\prime }_{\kappa }$
,
 $\phi \in \mathcal {L}_{\kappa \kappa }(X)$
, and
$\phi \in \mathcal {L}_{\kappa \kappa }(X)$
, and
 $X = Y \cup Z$
, we have
$X = Y \cup Z$
, we have
 $(\exists Y) \phi , (\forall Y) \phi \in \mathcal {L}_{\kappa \kappa }(Z)$
.Footnote
12
$(\exists Y) \phi , (\forall Y) \phi \in \mathcal {L}_{\kappa \kappa }(Z)$
.Footnote
12
We identify as usual two formulas
![]() $\phi , \psi \in \mathcal {L}_{\kappa \kappa }(X)$
in the same context if they differ only in change of bound variables. We denote variable substitution by
$\phi , \psi \in \mathcal {L}_{\kappa \kappa }(X)$
in the same context if they differ only in change of bound variables. We denote variable substitution by
for
![]() $f : Y \to X \in \mathsf {Set}^{\prime }_{\kappa }$
; we automatically extend f in the notation
$f : Y \to X \in \mathsf {Set}^{\prime }_{\kappa }$
; we automatically extend f in the notation
![]() $[f]\phi $
by the identity map if necessary (so that, e.g.,
$[f]\phi $
by the identity map if necessary (so that, e.g.,
![]() $[x \mapsto y]\phi $
makes sense even if
$[x \mapsto y]\phi $
makes sense even if
![]() $\phi $
has free variables besides x). An
$\phi $
has free variables besides x). An
![]() $\mathcal {L}_{\kappa \kappa }$
-theory
$\mathcal {L}_{\kappa \kappa }$
-theory
![]() $\mathcal {T}$
is a set of
$\mathcal {T}$
is a set of
![]() $\mathcal {L}_{\kappa \kappa }$
-sentences
$\mathcal {L}_{\kappa \kappa }$
-sentences
![]() $\mathcal {T} \subseteq \mathcal {L}_{\kappa \kappa }(\emptyset )$
.
$\mathcal {T} \subseteq \mathcal {L}_{\kappa \kappa }(\emptyset )$
.
We use a Gentzen sequent calculus-type proof system for
![]() $\mathcal {L}_{\kappa \kappa }$
. We will not give the full details, for which see, e.g., [Reference Johnstone17, Section D1.3]; however, we will mention some of the key features. Sentences being proved are always universally quantified implications or sequents
$\mathcal {L}_{\kappa \kappa }$
. We will not give the full details, for which see, e.g., [Reference Johnstone17, Section D1.3]; however, we will mention some of the key features. Sentences being proved are always universally quantified implications or sequents
![]() $(\forall X) (\phi \Rightarrow \psi )$
(sometimes written
$(\forall X) (\phi \Rightarrow \psi )$
(sometimes written
![]() $\phi \vdash _X \psi $
) between two formulas
$\phi \vdash _X \psi $
) between two formulas
![]() $\phi , \psi \in \mathcal {L}_{\kappa \kappa }(X)$
in the same context. Since we are dealing with an infinitary logic, it is important to note that we do not include any “complete distributivity” or “axiom of choice”-type inference rules connecting
$\phi , \psi \in \mathcal {L}_{\kappa \kappa }(X)$
in the same context. Since we are dealing with an infinitary logic, it is important to note that we do not include any “complete distributivity” or “axiom of choice”-type inference rules connecting
![]() $\bigwedge , \bigvee $
or
$\bigwedge , \bigvee $
or
![]() $\bigwedge , \exists $
(as would be required to make the proof system complete with respect to the usual semantics in set-based models), except for (AC) below. The actual inference rules are the obvious infinitary generalizations of [Reference Johnstone17, Definition D1.3.1(a–h)] (where the rules (f) and (g) must allow quantifiers over multiple variables) and the law of excluded middle, together with the following axiom schema:Footnote
13
$\bigwedge , \exists $
(as would be required to make the proof system complete with respect to the usual semantics in set-based models), except for (AC) below. The actual inference rules are the obvious infinitary generalizations of [Reference Johnstone17, Definition D1.3.1(a–h)] (where the rules (f) and (g) must allow quantifiers over multiple variables) and the law of excluded middle, together with the following axiom schema:Footnote
13
for
![]() $X = \bigsqcup\nolimits _i Y_i \sqcup Z \in \mathsf {Set}^{\prime }_{\kappa }$
(note the disjoint union) and
$X = \bigsqcup\nolimits _i Y_i \sqcup Z \in \mathsf {Set}^{\prime }_{\kappa }$
(note the disjoint union) and
![]() $\phi _i \in \mathcal {L}_{\kappa \kappa }(Y_i \sqcup Z)$
. We write as usual
$\phi _i \in \mathcal {L}_{\kappa \kappa }(Y_i \sqcup Z)$
. We write as usual
![]() $\mathcal {T} \vdash \sigma $
for a sequent
$\mathcal {T} \vdash \sigma $
for a sequent
![]() $\sigma $
if it is provable from the theory
$\sigma $
if it is provable from the theory
![]() $\mathcal {T}$
. We also slightly abuse terminology by referring to provability of certain sentences which are not sequents, with the obvious meanings: a universally quantified bi-implication
$\mathcal {T}$
. We also slightly abuse terminology by referring to provability of certain sentences which are not sequents, with the obvious meanings: a universally quantified bi-implication
![]() $(\forall X) (\phi \Leftrightarrow \psi )$
is provable iff both implications are; a general universally quantified formula
$(\forall X) (\phi \Leftrightarrow \psi )$
is provable iff both implications are; a general universally quantified formula
![]() $(\forall X) \phi $
is provable iff
$(\forall X) \phi $
is provable iff
![]() $(\forall X) (\top \Rightarrow \phi )$
is; etc.
$(\forall X) (\top \Rightarrow \phi )$
is; etc.
Given a theory
![]() $\mathcal {T}$
, we inductively define the class of
$\mathcal {T}$
, we inductively define the class of
![]() $\mathcal {T}$
-almost quantifier-free (or
$\mathcal {T}$
-almost quantifier-free (or
![]() $\mathcal {T}$
-aqf)
$\mathcal {T}$
-aqf)
![]() $\mathcal {L}_{\kappa \kappa }$
-formulas as follows, where by a
$\mathcal {L}_{\kappa \kappa }$
-formulas as follows, where by a
![]() $\mathcal {T}$
-aqf sequent we mean one between two
$\mathcal {T}$
-aqf sequent we mean one between two
![]() $\mathcal {T}$
-aqf formulas: a formula
$\mathcal {T}$
-aqf formulas: a formula
![]() $\phi $
is
$\phi $
is
![]() $\mathcal {T}$
-aqf if
$\mathcal {T}$
-aqf if
![]() $\phi $
does not contain
$\phi $
does not contain
![]() $\forall $
, and every existential subformula
$\forall $
, and every existential subformula
![]() $(\exists Y) \psi $
occurring in the construction of
$(\exists Y) \psi $
occurring in the construction of
![]() $\phi $
, where
$\phi $
, where
![]() $\psi \in \mathcal {L}_{\kappa \kappa }(X)$
with
$\psi \in \mathcal {L}_{\kappa \kappa }(X)$
with
![]() $X = Y \cup Z \in \mathsf {Set}^{\prime }_{\kappa }$
, is
$X = Y \cup Z \in \mathsf {Set}^{\prime }_{\kappa }$
, is
![]() $\mathcal {T}$
-provably unique, meaning
$\mathcal {T}$
-provably unique, meaning
where
![]() $Y \cong Y' \in \mathsf {Set}^{\prime }_{\kappa }$
is a copy of Y disjoint from X, and moreover this proof itself only involves
$Y \cong Y' \in \mathsf {Set}^{\prime }_{\kappa }$
is a copy of Y disjoint from X, and moreover this proof itself only involves
![]() $\mathcal {T}$
-aqf sequents. A theory
$\mathcal {T}$
-aqf sequents. A theory
![]() $\mathcal {T}$
is itself almost universal if there is a well-founded relation
$\mathcal {T}$
is itself almost universal if there is a well-founded relation
![]() $\prec $
on
$\prec $
on
![]() $\mathcal {T}$
such that each sentence in
$\mathcal {T}$
such that each sentence in
![]() $\mathcal {T}$
is an aqf sequent with respect to its
$\mathcal {T}$
is an aqf sequent with respect to its
![]() $\prec $
-predecessors. In other words,
$\prec $
-predecessors. In other words,
![]() $\mathcal {T}$
can be constructed by repeatedly adding aqf sequents with respect to the preexisting theory.
$\mathcal {T}$
can be constructed by repeatedly adding aqf sequents with respect to the preexisting theory.
We will only be considering aqf formulas and almost universal theories. Thus, we henceforth restrict the proof system to proofs involving only aqf sequents; in particular, we drop the inference rules for
![]() $\forall $
[Reference Johnstone17, Definition D1.3.1(g)]. When we say
$\forall $
[Reference Johnstone17, Definition D1.3.1(g)]. When we say
![]() $\mathcal {T}$
-provable, we mean using only
$\mathcal {T}$
-provable, we mean using only
![]() $\mathcal {T}$
-aqf sequents.
$\mathcal {T}$
-aqf sequents.
Let
![]() $\mathcal {L}_{\kappa \kappa }^{\mathcal {T}\mathrm {-aqf}}(X) \subseteq \mathcal {L}_{\kappa \kappa }(X)$
denote the subset of
$\mathcal {L}_{\kappa \kappa }^{\mathcal {T}\mathrm {-aqf}}(X) \subseteq \mathcal {L}_{\kappa \kappa }(X)$
denote the subset of
![]() $\mathcal {T}$
-aqf formulas. For
$\mathcal {T}$
-aqf formulas. For
![]() $\phi \in \mathcal {L}_{\kappa \kappa }^{\mathcal {T}\mathrm {-aqf}}(X)$
, let
$\phi \in \mathcal {L}_{\kappa \kappa }^{\mathcal {T}\mathrm {-aqf}}(X)$
, let
![]() $[\phi ] = [\phi ]_{\mathcal {T}}$
denote its
$[\phi ] = [\phi ]_{\mathcal {T}}$
denote its
![]() $\mathcal {T}$
-provable equivalence class, i.e.,
$\mathcal {T}$
-provable equivalence class, i.e.,
(using only
![]() $\mathcal {T}$
-aqf sequents). Let
$\mathcal {T}$
-aqf sequents). Let
denote the Lindenbaum–Tarski algebra of
![]() $\mathcal {T}$
-equivalence classes of
$\mathcal {T}$
-equivalence classes of
![]() $\mathcal {T}$
-aqf formulas, partially ordered by
$\mathcal {T}$
-aqf formulas, partially ordered by
![]() $\mathcal {T}$
-provable implication:
$\mathcal {T}$
-provable implication:
and with
![]() $\kappa $
-Boolean operations given by the logical connectives (which are easily seen to satisfy the
$\kappa $
-Boolean operations given by the logical connectives (which are easily seen to satisfy the
![]() $\kappa $
-Boolean algebra axioms mod
$\kappa $
-Boolean algebra axioms mod
![]() $\mathcal {T}$
-provability).
$\mathcal {T}$
-provability).
As X varies, these algebras are related via the variable substitution homomorphisms
for
![]() $f : X \to Y \in \mathsf {Set}^{\prime }_{\kappa }$
. We thus have a functorFootnote
14
$f : X \to Y \in \mathsf {Set}^{\prime }_{\kappa }$
. We thus have a functorFootnote
14
5.2 Syntactic categories and models
Let
![]() $\mathcal {T}$
be an almost universal
$\mathcal {T}$
be an almost universal
![]() $\mathcal {L}_{\kappa \kappa }$
-theory over a language
$\mathcal {L}_{\kappa \kappa }$
-theory over a language
![]() $\mathcal {L}$
. The syntactic category
$\mathcal {L}$
. The syntactic category
![]() ${\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle }$
has:
${\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle }$
has:
-
• objects: pairs
 $(X, \alpha )$
where
$(X, \alpha )$
where
 $X \in \mathsf {Set}^{\prime }_{\kappa }$
and
$X \in \mathsf {Set}^{\prime }_{\kappa }$
and
 $\alpha \in \mathcal {L}_{\kappa \kappa }^{\mathcal {T}\mathrm {-aqf}}(X)$
;
$\alpha \in \mathcal {L}_{\kappa \kappa }^{\mathcal {T}\mathrm {-aqf}}(X)$
; -
• morphisms
 $(X, \alpha ) \to (Y, \beta )$
:
$(X, \alpha ) \to (Y, \beta )$
:
 $\mathcal {T}$
-provable equivalence classes
$\mathcal {T}$
-provable equivalence classes
 $[\phi ] \in \mathcal {L}_{\kappa \kappa }^{\mathcal {T}\mathrm {-aqf}}(X \sqcup Y)/\mathcal {T}$
,Footnote
15
such that “
$[\phi ] \in \mathcal {L}_{\kappa \kappa }^{\mathcal {T}\mathrm {-aqf}}(X \sqcup Y)/\mathcal {T}$
,Footnote
15
such that “
 $\mathcal {T}$
proves that
$\mathcal {T}$
proves that
 $\phi $
is the graph of a function
$\phi $
is the graph of a function
 $\alpha \to \beta $
”, i.e., where
$\alpha \to \beta $
”, i.e., where $$ \begin{align*} \kern-6pt\mathcal{T} \vdash (\forall X \sqcup Y \sqcup Y') \Big( \phi \wedge [Y \to Y']\phi \Rightarrow \alpha \wedge \beta \wedge \bigwedge\nolimits_{Y \ni y \mapsto y' \in Y'} (y = y') \Big) &=: \sigma, \\\mathcal{T} \cup \{\sigma\} \vdash (\forall X) \Big( \alpha \Rightarrow (\exists Y) \phi \Big) &=: \tau, \end{align*} $$
$$ \begin{align*} \kern-6pt\mathcal{T} \vdash (\forall X \sqcup Y \sqcup Y') \Big( \phi \wedge [Y \to Y']\phi \Rightarrow \alpha \wedge \beta \wedge \bigwedge\nolimits_{Y \ni y \mapsto y' \in Y'} (y = y') \Big) &=: \sigma, \\\mathcal{T} \cup \{\sigma\} \vdash (\forall X) \Big( \alpha \Rightarrow (\exists Y) \phi \Big) &=: \tau, \end{align*} $$
 $Y' \cong Y$
is a disjoint copy of Y (note that
$Y' \cong Y$
is a disjoint copy of Y (note that
 $\tau $
is
$\tau $
is
 $(\mathcal {T} \cup \{\sigma \})$
-aqf).
$(\mathcal {T} \cup \{\sigma \})$
-aqf).
Proposition 5.1.
![]() ${\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle }$
is a
${\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle }$
is a
![]() $\kappa $
-complete Boolean
$\kappa $
-complete Boolean
![]() $\kappa $
-subextensive category, with:
$\kappa $
-subextensive category, with:
-
• identity
 $1_{(X, \alpha )} : (X, \alpha ) \to (X, \alpha )$
given by
$1_{(X, \alpha )} : (X, \alpha ) \to (X, \alpha )$
given by
 $[\alpha \wedge \bigwedge\nolimits _{X \ni x \mapsto x' \in X'} (x = x')]$
(where
$[\alpha \wedge \bigwedge\nolimits _{X \ni x \mapsto x' \in X'} (x = x')]$
(where
 $X'$
is a disjoint copy of X);
$X'$
is a disjoint copy of X); -
• composition of
 $[\phi ] : (X, \alpha ) \to (Y, \beta )$
and
$[\phi ] : (X, \alpha ) \to (Y, \beta )$
and
 $[\psi ] : (Y, \beta ) \to (Z, \gamma )$
given by
$[\psi ] : (Y, \beta ) \to (Z, \gamma )$
given by
 $[(\exists Y) (\phi \wedge \psi )]$
;
$[(\exists Y) (\phi \wedge \psi )]$
; -
• product of
 $(X_i, \alpha _i)$
, for
$(X_i, \alpha _i)$
, for
 $i \in I \in \mathsf {Set}^{\prime }_{\kappa }$
, given by
$i \in I \in \mathsf {Set}^{\prime }_{\kappa }$
, given by
 $(\bigsqcup\nolimits _i X_i, \bigwedge\nolimits _i \alpha _i)$
;
$(\bigsqcup\nolimits _i X_i, \bigwedge\nolimits _i \alpha _i)$
; -
• equalizer of
 $[\phi ], [\psi ] : (X, \alpha ) \to (Y, \beta )$
given by
$[\phi ], [\psi ] : (X, \alpha ) \to (Y, \beta )$
given by
 $(X, (\exists Y) (\phi \wedge \psi ))$
;
$(X, (\exists Y) (\phi \wedge \psi ))$
; -
• a morphism
 $[\phi ] : (X, \alpha ) \to (Y, \beta )$
monic iff
$[\phi ] : (X, \alpha ) \to (Y, \beta )$
monic iff
 $(\exists X) \phi $
is
$(\exists X) \phi $
is
 $\mathcal {T}$
-provably unique;
$\mathcal {T}$
-provably unique; -
• subobjects of
 $(X, \alpha )$
given by
$(X, \alpha )$
given by 
-
• join of a
 $\kappa $
-ary family of
$\kappa $
-ary family of
 $(X, \phi _i) \hookrightarrow (X, \alpha )$
given by
$(X, \phi _i) \hookrightarrow (X, \alpha )$
given by
 $(X, \bigvee _i \phi _i) \hookrightarrow (X, \alpha )$
;
$(X, \bigvee _i \phi _i) \hookrightarrow (X, \alpha )$
; -
• nonempty meet of
 $(X, \phi _i) \hookrightarrow (X, \alpha )$
given by
$(X, \phi _i) \hookrightarrow (X, \alpha )$
given by
 $(X, \bigwedge\nolimits _i \phi _i) \hookrightarrow (X, \alpha )$
;
$(X, \bigwedge\nolimits _i \phi _i) \hookrightarrow (X, \alpha )$
; -
• complement of
 $(X, \phi ) \hookrightarrow (X, \alpha )$
given by
$(X, \phi ) \hookrightarrow (X, \alpha )$
given by
 $(X, \alpha \wedge \neg \phi ) \hookrightarrow (X, \alpha )$
;
$(X, \alpha \wedge \neg \phi ) \hookrightarrow (X, \alpha )$
; -
• pullback of a subobject
 $(X, \phi ) \hookrightarrow (X, \top )$
corresponding to
$(X, \phi ) \hookrightarrow (X, \top )$
corresponding to
 $[\phi ] \in \mathcal {L}_{\kappa \kappa }^{\mathcal {T}\mathrm {-aqf}}(X)/\mathcal {T}$
along a morphism of the form
$[\phi ] \in \mathcal {L}_{\kappa \kappa }^{\mathcal {T}\mathrm {-aqf}}(X)/\mathcal {T}$
along a morphism of the form
 $(\pi _{f(x)})_{x \in X} : (Y, \top ) \cong (1, \top )^Y \to (1, \top )^X \cong (X, \top )$
for some
$(\pi _{f(x)})_{x \in X} : (Y, \top ) \cong (1, \top )^Y \to (1, \top )^X \cong (X, \top )$
for some
 $f : X \to Y$
, where
$f : X \to Y$
, where
 $\pi _y : \prod _{y \in Y} (1, \top ) \to (1, \top )$
is the yth projection, given by the variable substitution
$\pi _y : \prod _{y \in Y} (1, \top ) \to (1, \top )$
is the yth projection, given by the variable substitution
 $[f] : \mathcal {L}_{\kappa \kappa }^{\mathcal {T}\mathrm {-aqf}}(X)/\mathcal {T} \to \mathcal {L}_{\kappa \kappa }^{\mathcal {T}\mathrm {-aqf}}(Y)/\mathcal {T}$
.
$[f] : \mathcal {L}_{\kappa \kappa }^{\mathcal {T}\mathrm {-aqf}}(X)/\mathcal {T} \to \mathcal {L}_{\kappa \kappa }^{\mathcal {T}\mathrm {-aqf}}(Y)/\mathcal {T}$
.
Proof By straightforward constructions of explicit proofs witnessing the necessary conditions; see [Reference Johnstone17, Section D1.4] and [Reference Makkai and Reyes23, Proposition 8.2.1] for details (in the finitary case; the
![]() $\kappa $
-ary case is analogous). We only comment on the role of (AC), which is used to check the universal property of the product
$\kappa $
-ary case is analogous). We only comment on the role of (AC), which is used to check the universal property of the product
![]() $\prod _i (X_i, \alpha _i) = (\bigsqcup\nolimits _i X_i, \bigwedge\nolimits _i \alpha _i)$
: given a cone
$\prod _i (X_i, \alpha _i) = (\bigsqcup\nolimits _i X_i, \bigwedge\nolimits _i \alpha _i)$
: given a cone
![]() $([\phi _i] : (Y, \beta ) \to (X_i, \alpha _i))_i$
, the induced morphism
$([\phi _i] : (Y, \beta ) \to (X_i, \alpha _i))_i$
, the induced morphism
![]() $(Y, \beta ) \to (\bigsqcup\nolimits _i X_i, \bigwedge\nolimits _i \alpha _i)$
is given by
$(Y, \beta ) \to (\bigsqcup\nolimits _i X_i, \bigwedge\nolimits _i \alpha _i)$
is given by
![]() $[\bigwedge\nolimits _i \phi _i]$
; to check the totality condition in the definition of morphism, we need
$[\bigwedge\nolimits _i \phi _i]$
; to check the totality condition in the definition of morphism, we need
![]() $\beta \Rightarrow (\exists \bigsqcup\nolimits _i X_i) (\bigwedge\nolimits _i \phi _i)$
, which follows from
$\beta \Rightarrow (\exists \bigsqcup\nolimits _i X_i) (\bigwedge\nolimits _i \phi _i)$
, which follows from
![]() $\beta \Rightarrow \bigwedge\nolimits _i (\exists X_i) \phi _i$
(because each
$\beta \Rightarrow \bigwedge\nolimits _i (\exists X_i) \phi _i$
(because each
![]() $[\phi _i]$
is a morphism) and
$[\phi _i]$
is a morphism) and
![]() $\bigwedge\nolimits _i (\exists X_i) \phi _i \Rightarrow (\exists \bigsqcup\nolimits _i X_i) (\bigwedge\nolimits _i \phi _i)$
by (AC).
$\bigwedge\nolimits _i (\exists X_i) \phi _i \Rightarrow (\exists \bigsqcup\nolimits _i X_i) (\bigwedge\nolimits _i \phi _i)$
by (AC).
We have a distinguished object
![]() $H := (1, \top ) \in {\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle }$
, whose
$H := (1, \top ) \in {\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle }$
, whose
![]() $\kappa $
-ary powers are by Proposition 5.1 given by
$\kappa $
-ary powers are by Proposition 5.1 given by
![]() $H^X = (X, \bigwedge\nolimits _i \top ) \cong (X, \top )$
for each
$H^X = (X, \bigwedge\nolimits _i \top ) \cong (X, \top )$
for each
![]() $X \in \mathsf {Set}^{\prime }_{\kappa }$
, and each relation symbol
$X \in \mathsf {Set}^{\prime }_{\kappa }$
, and each relation symbol
![]() $R \in \mathcal {L}(X)$
yields a subobject
$R \in \mathcal {L}(X)$
yields a subobject
![]() $R^{\mathcal {H}} := (X, R(1_X)) \hookrightarrow (X, \top ) = H^X \in {\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle }$
. We next show that
$R^{\mathcal {H}} := (X, R(1_X)) \hookrightarrow (X, \top ) = H^X \in {\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle }$
. We next show that
![]() ${\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle }$
is the
${\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle }$
is the
![]() $\kappa $
-complete Boolean
$\kappa $
-complete Boolean
![]() $\kappa $
-subextensive category “freely generated by an object H, together with subobjects
$\kappa $
-subextensive category “freely generated by an object H, together with subobjects
![]() $R^{\mathcal {H}} \subseteq H^X$
for each
$R^{\mathcal {H}} \subseteq H^X$
for each
![]() $R \in \mathcal {L}(X)$
, satisfying the relations in
$R \in \mathcal {L}(X)$
, satisfying the relations in
![]() $\mathcal {T}$
”. This requires defining the category of all such data in an arbitrary
$\mathcal {T}$
”. This requires defining the category of all such data in an arbitrary
![]() $\kappa $
-complete Boolean
$\kappa $
-complete Boolean
![]() $\kappa $
-subextensive category
$\kappa $
-subextensive category
![]() $\mathsf {C}$
, i.e., the notion of a model of
$\mathsf {C}$
, i.e., the notion of a model of
![]() $\mathcal {T}$
in
$\mathcal {T}$
in
![]() $\mathsf {C}$
; see [Reference Johnstone17, Section D1.2] and [Reference Makkai and Reyes23, Section 2.3] for the finitary case.
$\mathsf {C}$
; see [Reference Johnstone17, Section D1.2] and [Reference Makkai and Reyes23, Section 2.3] for the finitary case.
Let
![]() $\mathcal {L}$
be a language and
$\mathcal {L}$
be a language and
![]() $\mathsf {C}$
be a
$\mathsf {C}$
be a
![]() $\kappa $
-complete Boolean
$\kappa $
-complete Boolean
![]() $\kappa $
-subextensive category. An
$\kappa $
-subextensive category. An
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {M} = (M, R^{\mathcal {M}})_{R \in \mathcal {L}}$
in
$\mathcal {M} = (M, R^{\mathcal {M}})_{R \in \mathcal {L}}$
in
![]() $\mathsf {C}$
consists of:
$\mathsf {C}$
consists of:
-
• an underlying object
 $M \in \mathsf {C}$
;
$M \in \mathsf {C}$
; -
• for each relation symbol
 $R \in \mathcal {L}(X)$
, a subobject
$R \in \mathcal {L}(X)$
, a subobject
 $R^{\mathcal {M}} \subseteq \prod M^X\kern-1pt $
, called the interpretation of R in
$R^{\mathcal {M}} \subseteq \prod M^X\kern-1pt $
, called the interpretation of R in
 $\mathcal {M}$
.
$\mathcal {M}$
.
Given an
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {M}$
in
$\mathcal {M}$
in
![]() $\mathsf {C}$
, we inductively define for certain
$\mathsf {C}$
, we inductively define for certain
![]() $\forall $
-free
$\forall $
-free
![]() $\mathcal {L}_{\kappa \kappa }$
-formulas
$\mathcal {L}_{\kappa \kappa }$
-formulas
![]() $\phi \in \mathcal {L}_{\kappa \kappa }(X)$
an interpretation
$\phi \in \mathcal {L}_{\kappa \kappa }(X)$
an interpretation
![]() $\phi ^{\mathcal {M}} \subseteq H^X$
of
$\phi ^{\mathcal {M}} \subseteq H^X$
of
![]() $\phi $
in
$\phi $
in
![]() $\mathcal {M}$
, as follows; we say that
$\mathcal {M}$
, as follows; we say that
![]() $\phi $
is interpretable in
$\phi $
is interpretable in
![]() $\mathcal {M}$
if it has an interpretation.
$\mathcal {M}$
if it has an interpretation.
-
• An atomic formula
 $R(\vec {x}) \in \mathcal {L}_{\kappa \kappa }(X)$
, where
$R(\vec {x}) \in \mathcal {L}_{\kappa \kappa }(X)$
, where
 $\vec {x} \in X^Y$
and
$\vec {x} \in X^Y$
and
 $R \in \mathcal {L}(Y)$
, is interpreted as the pullback of
$R \in \mathcal {L}(Y)$
, is interpreted as the pullback of
 $R^{\mathcal {M}} \subseteq M^Y$
along
$R^{\mathcal {M}} \subseteq M^Y$
along
 $(\pi _{x_y})_{y \in Y} : M^X \to M^Y$
(where
$(\pi _{x_y})_{y \in Y} : M^X \to M^Y$
(where
 $\pi _x : M^X \to M$
is the xth projection).
$\pi _x : M^X \to M$
is the xth projection). -
• An atomic formula
 $(x = y) \in \mathcal {L}_{\kappa \kappa }(X)$
, where
$(x = y) \in \mathcal {L}_{\kappa \kappa }(X)$
, where
 $x, y \in X$
, is interpreted as the equalizer of the projections
$x, y \in X$
, is interpreted as the equalizer of the projections
 $\pi _x, \pi _y : M^X \to M$
.
$\pi _x, \pi _y : M^X \to M$
. -
• If
 $\phi , \phi _i \in \mathcal {L}_{\kappa \kappa }(X)$
(
$\phi , \phi _i \in \mathcal {L}_{\kappa \kappa }(X)$
(
 $I \in \mathsf {Set}^{\prime }_{\kappa }$
) are interpretable in
$I \in \mathsf {Set}^{\prime }_{\kappa }$
) are interpretable in
 $\mathcal {M}$
, then so are
$\mathcal {M}$
, then so are
 $\neg \phi , \bigvee _i \phi _i, \bigwedge\nolimits _i \phi _i \in \mathcal {L}_{\kappa \kappa }(X)$
, given by applying the corresponding
$\neg \phi , \bigvee _i \phi _i, \bigwedge\nolimits _i \phi _i \in \mathcal {L}_{\kappa \kappa }(X)$
, given by applying the corresponding
 $\kappa $
-Boolean operations in
$\kappa $
-Boolean operations in
 $\mathrm {Sub}_{\mathsf {C}}(M^X)$
.
$\mathrm {Sub}_{\mathsf {C}}(M^X)$
. -
• If
 $\phi \in \mathcal {L}_{\kappa \kappa }(X)$
is interpretable, where
$\phi \in \mathcal {L}_{\kappa \kappa }(X)$
is interpretable, where
 $X = Y \cup Z$
, and the composite (where
$X = Y \cup Z$
, and the composite (where $$ \begin{align*} \phi^{\mathcal{M}} \hookrightarrow M^X \xrightarrow{\pi_{X \setminus Y}} M^{X \setminus Y} \end{align*} $$
$$ \begin{align*} \phi^{\mathcal{M}} \hookrightarrow M^X \xrightarrow{\pi_{X \setminus Y}} M^{X \setminus Y} \end{align*} $$
 $\pi _{X \setminus Y}$
is the projection) is monic, then
$\pi _{X \setminus Y}$
is the projection) is monic, then
 $(\exists Y) \phi \in \mathcal {L}_{\kappa \kappa }(Z)$
is interpreted as the pullback of this composite along the projection
$(\exists Y) \phi \in \mathcal {L}_{\kappa \kappa }(Z)$
is interpreted as the pullback of this composite along the projection
 $M^Z \to M^{X \setminus Y}$
.
$M^Z \to M^{X \setminus Y}$
.
A sentence
![]() $\sigma = (\forall X) \phi $
with
$\sigma = (\forall X) \phi $
with
![]() $\phi \, \forall $
-free is interpretable in
$\phi \, \forall $
-free is interpretable in
![]() $\mathcal {M}$
if
$\mathcal {M}$
if
![]() $\phi $
is, and satisfied in
$\phi $
is, and satisfied in
![]() $\mathcal {M}$
, written
$\mathcal {M}$
, written
![]() $\mathcal {M} \models \sigma $
, if
$\mathcal {M} \models \sigma $
, if
![]() $\phi ^{\mathcal {M}} = M^X$
(thus if
$\phi ^{\mathcal {M}} = M^X$
(thus if
![]() $\sigma = (\forall X) (\phi \Rightarrow \psi )$
is a sequent, this is equivalent to
$\sigma = (\forall X) (\phi \Rightarrow \psi )$
is a sequent, this is equivalent to
![]() $\phi ^{\mathcal {M}} \subseteq \psi ^{\mathcal {M}} \subseteq M^X$
). For a theory
$\phi ^{\mathcal {M}} \subseteq \psi ^{\mathcal {M}} \subseteq M^X$
). For a theory
![]() $\mathcal {T}$
,
$\mathcal {T}$
,
![]() $\mathcal {M}$
is a model of
$\mathcal {M}$
is a model of
![]() $\mathcal {T}$
, written
$\mathcal {T}$
, written
![]() $\mathcal {M} \models \mathcal {T}$
, if every
$\mathcal {M} \models \mathcal {T}$
, if every
![]() $\sigma \in \mathcal {T}$
is satisfied in
$\sigma \in \mathcal {T}$
is satisfied in
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Proposition 5.2 (Soundness)
If
![]() $\mathcal {M} \models \mathcal {T}$
, then every
$\mathcal {M} \models \mathcal {T}$
, then every
![]() $\mathcal {T}$
-aqf formula is interpretable in
$\mathcal {T}$
-aqf formula is interpretable in
![]() $\mathcal {M}$
, and every
$\mathcal {M}$
, and every
![]() $\mathcal {T}$
-aqf sequent
$\mathcal {T}$
-aqf sequent
![]() $(\forall X) (\phi \Rightarrow \psi )$
proved by
$(\forall X) (\phi \Rightarrow \psi )$
proved by
![]() $\mathcal {T}$
is satisfied in
$\mathcal {T}$
is satisfied in
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Proof First, one proves by an easy induction that interpretation of formulas in
![]() $\mathcal {M}$
is preserved under variable substitutions: for
$\mathcal {M}$
is preserved under variable substitutions: for
![]() $f : Y \to X \in \mathsf {Set}^{\prime }_{\kappa }$
, if
$f : Y \to X \in \mathsf {Set}^{\prime }_{\kappa }$
, if
![]() $\phi \in \mathcal {L}_{\kappa \kappa }(Y)$
is interpretable, then so is
$\phi \in \mathcal {L}_{\kappa \kappa }(Y)$
is interpretable, then so is
![]() $[f]\phi \in \mathcal {L}_{\kappa \kappa }(X)$
, given by the pullback of
$[f]\phi \in \mathcal {L}_{\kappa \kappa }(X)$
, given by the pullback of
![]() $\phi ^{\mathcal {M}} \subseteq M^Y$
along
$\phi ^{\mathcal {M}} \subseteq M^Y$
along
![]() $(\pi _{f(y)})_{y \in Y} : M^X \to M^Y$
.
$(\pi _{f(y)})_{y \in Y} : M^X \to M^Y$
.
Next, one proves by induction that if a sequent interpretable in
![]() $\mathcal {M}$
(but not yet known to be
$\mathcal {M}$
(but not yet known to be
![]() $\mathcal {T}$
-aqf) is proved by
$\mathcal {T}$
-aqf) is proved by
![]() $\mathcal {T}$
using only other sequents interpretable in
$\mathcal {T}$
using only other sequents interpretable in
![]() $\mathcal {M}$
, then it must be satisfied in
$\mathcal {M}$
, then it must be satisfied in
![]() $\mathcal {M}$
. This is again straightforward (see [Reference Johnstone17, Proposition D1.3.2]). Again, we only verify (AC). Let
$\mathcal {M}$
. This is again straightforward (see [Reference Johnstone17, Proposition D1.3.2]). Again, we only verify (AC). Let
![]() $X = \bigsqcup\nolimits _i Y_i \sqcup Z \in \mathsf {Set}^{\prime }_{\kappa }$
and
$X = \bigsqcup\nolimits _i Y_i \sqcup Z \in \mathsf {Set}^{\prime }_{\kappa }$
and
![]() $\phi _i \in \mathcal {L}_{\kappa \kappa }(Y_i \sqcup Z)$
; we must show that
$\phi _i \in \mathcal {L}_{\kappa \kappa }(Y_i \sqcup Z)$
; we must show that
assuming that the left (and right) interpretation is defined. Interpretability of
![]() $(\exists Y_i) \phi _i \in \mathcal {L}_{\kappa \kappa }(Z)$
means that
$(\exists Y_i) \phi _i \in \mathcal {L}_{\kappa \kappa }(Z)$
means that
![]() $\phi _i \in \mathcal {L}_{\kappa \kappa }(Y_i \sqcup Z)$
is interpretable, and the composite
$\phi _i \in \mathcal {L}_{\kappa \kappa }(Y_i \sqcup Z)$
is interpretable, and the composite
(the second map is the projection) is monic; this composite is then
![]() $((\exists Y_i) \phi _i)^{\mathcal {M}} \subseteq M^Z$
. The wide pullback of all these composites is then
$((\exists Y_i) \phi _i)^{\mathcal {M}} \subseteq M^Z$
. The wide pullback of all these composites is then
![]() $(\bigwedge\nolimits _i (\exists Y_i) \phi _i)^{\mathcal {M}} \subseteq M^Z$
. By standard facts about pullbacks (e.g., do the calculation in
$(\bigwedge\nolimits _i (\exists Y_i) \phi _i)^{\mathcal {M}} \subseteq M^Z$
. By standard facts about pullbacks (e.g., do the calculation in
![]() $\mathsf {Set}$
using Yoneda), this wide pullback is the composite of the wide pullback of the pullbacks of
$\mathsf {Set}$
using Yoneda), this wide pullback is the composite of the wide pullback of the pullbacks of
![]() $\phi _i^{\mathcal {M}} \hookrightarrow M^{Y_i \sqcup Z}$
along the projections
$\phi _i^{\mathcal {M}} \hookrightarrow M^{Y_i \sqcup Z}$
along the projections
![]() $M^X \to M^{Y_i \sqcup Z}$
, with the projection
$M^X \to M^{Y_i \sqcup Z}$
, with the projection
![]() $M^X \to M^Z$
, which is exactly
$M^X \to M^Z$
, which is exactly
![]() $((\exists \bigcup\nolimits _i Y_i) (\bigwedge\nolimits_i \phi _i))^{\mathcal {M}}$
(this uses the first part of the proof to relate the interpretations of
$((\exists \bigcup\nolimits _i Y_i) (\bigwedge\nolimits_i \phi _i))^{\mathcal {M}}$
(this uses the first part of the proof to relate the interpretations of
![]() $\phi _i \in \mathcal {L}_{\kappa \kappa }(Y_i \sqcup Z)$
and
$\phi _i \in \mathcal {L}_{\kappa \kappa }(Y_i \sqcup Z)$
and
![]() $\phi _i \in \mathcal {L}_{\kappa \kappa }(X)$
).
$\phi _i \in \mathcal {L}_{\kappa \kappa }(X)$
).
Finally, one proves that every
![]() $\mathcal {T}$
-aqf formula is interpretable in
$\mathcal {T}$
-aqf formula is interpretable in
![]() $\mathcal {M}$
, by induction on the definition of
$\mathcal {M}$
, by induction on the definition of
![]() $\mathcal {T}$
-aqf. This uses a nested induction on the formula in question, using that the “
$\mathcal {T}$
-aqf. This uses a nested induction on the formula in question, using that the “
![]() $\mathcal {T}$
-provably unique” condition in the definition of
$\mathcal {T}$
-provably unique” condition in the definition of
![]() $\mathcal {T}$
-aqf (which is satisfied in
$\mathcal {T}$
-aqf (which is satisfied in
![]() $\mathcal {M}$
by the previous part of the proof and the outer induction hypothesis) exactly translates to the condition for an existential quantifier to be interpretable.
$\mathcal {M}$
by the previous part of the proof and the outer induction hypothesis) exactly translates to the condition for an existential quantifier to be interpretable.
Corollary 5.3. If
![]() $\mathcal {T}$
is almost universal, then either
$\mathcal {T}$
is almost universal, then either
![]() $\mathcal {M} \models \mathcal {T}$
, or there is a sequent in
$\mathcal {M} \models \mathcal {T}$
, or there is a sequent in
![]() $\mathcal {T}$
which is interpretable but not satisfied in
$\mathcal {T}$
which is interpretable but not satisfied in
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Proof By induction on the well-founded relation witnessing that
![]() $\mathcal {T}$
is almost universal.
$\mathcal {T}$
is almost universal.
Let
![]() $\mathcal {T}$
be an almost universal theory. For two models
$\mathcal {T}$
be an almost universal theory. For two models
![]() $\mathcal {M}, \mathcal {N} \models \mathcal {T}$
in
$\mathcal {M}, \mathcal {N} \models \mathcal {T}$
in
![]() $\mathsf {C}$
, a
$\mathsf {C}$
, a
![]() $\mathcal {T}$
-aqf embedding
$\mathcal {T}$
-aqf embedding
![]() $f : \mathcal {M} \to \mathcal {N}$
is a morphism
$f : \mathcal {M} \to \mathcal {N}$
is a morphism
![]() $f : M \to N \in \mathsf {C}$
such that for every
$f : M \to N \in \mathsf {C}$
such that for every
![]() $\mathcal {T}$
-aqf formula
$\mathcal {T}$
-aqf formula
![]() $\phi \in \mathcal {L}_{\kappa \kappa }^{\mathcal {T}\mathrm {-aqf}}(X)$
, the induced morphism
$\phi \in \mathcal {L}_{\kappa \kappa }^{\mathcal {T}\mathrm {-aqf}}(X)$
, the induced morphism
![]() $f^X : M^X \to N^X$
restricts to a (necessarily unique) morphism
$f^X : M^X \to N^X$
restricts to a (necessarily unique) morphism
![]() $\phi ^{\mathcal {M}} \to \phi ^{\mathcal {N}}$
:Footnote
16
$\phi ^{\mathcal {M}} \to \phi ^{\mathcal {N}}$
:Footnote
16

Let
![]() $\mathsf {\mathcal {T}\text{-}Mod}(\mathsf {C})$
be the category of models of
$\mathsf {\mathcal {T}\text{-}Mod}(\mathsf {C})$
be the category of models of
![]() $\mathcal {T}$
in
$\mathcal {T}$
in
![]() $\mathsf {C}$
and
$\mathsf {C}$
and
![]() $\mathcal {T}$
-aqf embeddings.
$\mathcal {T}$
-aqf embeddings.
Since the definition of
![]() $\mathcal {L}$
-structure in
$\mathcal {L}$
-structure in
![]() $\mathsf {C}$
and the interpretation of
$\mathsf {C}$
and the interpretation of
![]() $\mathcal {T}$
-aqf formulas only use the
$\mathcal {T}$
-aqf formulas only use the
![]() $\kappa $
-complete Boolean
$\kappa $
-complete Boolean
![]() $\kappa $
-subextensive structure of
$\kappa $
-subextensive structure of
![]() $\mathsf {C}$
, we may push forward a model
$\mathsf {C}$
, we may push forward a model
![]() $\mathcal {M} \in \mathsf {\mathcal {T}\text{-}Mod}(\mathsf {C})$
across a
$\mathcal {M} \in \mathsf {\mathcal {T}\text{-}Mod}(\mathsf {C})$
across a
![]() $\kappa $
-continuous
$\kappa $
-continuous
![]() $\kappa $
-subextensive functor
$\kappa $
-subextensive functor
![]() $\mathcal {F} : \mathsf {C} \to \mathsf {D}$
, for another
$\mathcal {F} : \mathsf {C} \to \mathsf {D}$
, for another
![]() $\kappa $
-complete Boolean
$\kappa $
-complete Boolean
![]() $\kappa $
-subextensive category
$\kappa $
-subextensive category
![]() $\mathsf {D}$
, to obtain a model
$\mathsf {D}$
, to obtain a model
which has the property that
![]() $\mathcal {F}(\phi ^{\mathcal {M}}) = \phi ^{\mathcal {F}(\mathcal {M})} \subseteq \mathcal {F}(M)^X \cong \mathcal {F}(M^X)$
for any
$\mathcal {F}(\phi ^{\mathcal {M}}) = \phi ^{\mathcal {F}(\mathcal {M})} \subseteq \mathcal {F}(M)^X \cong \mathcal {F}(M^X)$
for any
![]() $\phi \in \mathcal {L}_{\kappa \kappa }^{\mathcal {T}\mathrm {-aqf}}(X)$
. Thus, for every
$\phi \in \mathcal {L}_{\kappa \kappa }^{\mathcal {T}\mathrm {-aqf}}(X)$
. Thus, for every
![]() $\mathcal {T}$
-aqf embedding
$\mathcal {T}$
-aqf embedding
![]() $f : \mathcal {M} \to \mathcal {N} \in \mathsf {\mathcal {T}\text{-}Mod}(\mathsf {C})$
, its
$f : \mathcal {M} \to \mathcal {N} \in \mathsf {\mathcal {T}\text{-}Mod}(\mathsf {C})$
, its
![]() $\mathcal {F}$
-image
$\mathcal {F}$
-image
![]() $\mathcal {F}(f) : \mathcal {F}(M) \to \mathcal {F}(N) \in \mathsf {D}$
is a
$\mathcal {F}(f) : \mathcal {F}(M) \to \mathcal {F}(N) \in \mathsf {D}$
is a
![]() $\mathcal {T}$
-aqf embedding
$\mathcal {T}$
-aqf embedding
![]() $\mathcal {F}(\mathcal {M}) \to \mathcal {F}(N) \in \mathsf {\mathcal {T}\text{-}Mod}(\mathsf {D})$
. So
$\mathcal {F}(\mathcal {M}) \to \mathcal {F}(N) \in \mathsf {\mathcal {T}\text{-}Mod}(\mathsf {D})$
. So
![]() $\mathcal {F} : \mathsf {C} \to \mathsf {D} \in \kappa \mathfrak {LimBSExtCat}$
induces a functor
$\mathcal {F} : \mathsf {C} \to \mathsf {D} \in \kappa \mathfrak {LimBSExtCat}$
induces a functor
For a natural transformation
![]() $\xi : \mathcal {F} \to \mathcal {G} : \mathsf {C} \to \mathsf {D} \in \kappa \mathfrak {LimBSExtCat}$
, for any model
$\xi : \mathcal {F} \to \mathcal {G} : \mathsf {C} \to \mathsf {D} \in \kappa \mathfrak {LimBSExtCat}$
, for any model
![]() $\mathcal {M} \in \mathsf {\mathcal {T}\text{-}Mod}(\mathsf {C})$
, the component
$\mathcal {M} \in \mathsf {\mathcal {T}\text{-}Mod}(\mathsf {C})$
, the component
![]() $\xi _M : \mathcal {F}(M) \to \mathcal {G}(M)$
is a
$\xi _M : \mathcal {F}(M) \to \mathcal {G}(M)$
is a
![]() $\mathcal {T}$
-aqf embedding
$\mathcal {T}$
-aqf embedding
![]() $\mathcal {F}(\mathcal {M}) \to \mathcal {G}(\mathcal {M})$
, since for any
$\mathcal {F}(\mathcal {M}) \to \mathcal {G}(\mathcal {M})$
, since for any
![]() $\phi \in \mathcal {L}_{\kappa \kappa }^{\mathcal {T}\mathrm {-aqf}}(X)$
, by naturality of
$\phi \in \mathcal {L}_{\kappa \kappa }^{\mathcal {T}\mathrm {-aqf}}(X)$
, by naturality of
![]() $\xi $
we have a commutative square
$\xi $
we have a commutative square

thus
![]() $\xi $
lifts to a natural transformation
$\xi $
lifts to a natural transformation
with components
![]() $\mathsf {\mathcal {T}\text{-}Mod}(\xi )_{\mathcal {M}} := \xi _{\mathcal {M}} := \xi _M$
for
$\mathsf {\mathcal {T}\text{-}Mod}(\xi )_{\mathcal {M}} := \xi _{\mathcal {M}} := \xi _M$
for
![]() $\mathcal {M} \in \mathsf {\mathcal {T}\text{-}Mod}(\mathsf {C})$
. So we have a (strict) 2-functor
$\mathcal {M} \in \mathsf {\mathcal {T}\text{-}Mod}(\mathsf {C})$
. So we have a (strict) 2-functor
Returning to the syntactic category
![]() ${\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle }$
, the object
${\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle }$
, the object
![]() $H = (1, \top ) \in {\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle }$
together with the subobjects
$H = (1, \top ) \in {\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle }$
together with the subobjects
![]() $R^{\mathcal {H}} = (X, R(1_X)) \subseteq H^X$
forms an
$R^{\mathcal {H}} = (X, R(1_X)) \subseteq H^X$
forms an
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {H} = \mathcal {H}_{\mathcal {T}}$
in
$\mathcal {H} = \mathcal {H}_{\mathcal {T}}$
in
![]() ${\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle }$
, for which it is easily seen by induction that
${\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle }$
, for which it is easily seen by induction that
![]() $\phi ^{\mathcal {H}} = (X, \phi ) \subseteq H^X$
for any
$\phi ^{\mathcal {H}} = (X, \phi ) \subseteq H^X$
for any
![]() $\phi \in \mathcal {L}_{\kappa \kappa }^{\mathcal {T}\mathrm {-aqf}}(X)$
, whence
$\phi \in \mathcal {L}_{\kappa \kappa }^{\mathcal {T}\mathrm {-aqf}}(X)$
, whence
![]() $\mathcal {H}$
is a model of
$\mathcal {H}$
is a model of
![]() $\mathcal {T}$
, called the universal model. We may finally state the universal property of
$\mathcal {T}$
, called the universal model. We may finally state the universal property of
![]() ${\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle }$
:
${\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle }$
:
Proposition 5.4. For any other
![]() $\kappa $
-complete Boolean
$\kappa $
-complete Boolean
![]() $\kappa $
-subextensive category
$\kappa $
-subextensive category
![]() $\mathsf {C}$
, we have an equivalence of categories
$\mathsf {C}$
, we have an equivalence of categories
 $$ \begin{align*} \kappa\mathfrak{LimBSExtCat}({\langle}{\mathcal{L} \mid \mathcal{T}}{\rangle}, \mathsf{C}) &\longrightarrow \mathsf{\mathcal{T}\text{-}Mod}(\mathsf{C}) \\ \mathcal{F} &\longmapsto \mathcal{F}(\mathcal{H}) \\ (\xi : \mathcal{F} \to \mathcal{G}) &\longmapsto \xi_{\mathcal{H}}. \end{align*} $$
$$ \begin{align*} \kappa\mathfrak{LimBSExtCat}({\langle}{\mathcal{L} \mid \mathcal{T}}{\rangle}, \mathsf{C}) &\longrightarrow \mathsf{\mathcal{T}\text{-}Mod}(\mathsf{C}) \\ \mathcal{F} &\longmapsto \mathcal{F}(\mathcal{H}) \\ (\xi : \mathcal{F} \to \mathcal{G}) &\longmapsto \xi_{\mathcal{H}}. \end{align*} $$
(In other words,
![]() $\mathcal {H} \in \mathsf {\mathcal {T}\text{-}Mod}({\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle })$
is a (non-strict) representation of the 2-presheaf
$\mathcal {H} \in \mathsf {\mathcal {T}\text{-}Mod}({\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle })$
is a (non-strict) representation of the 2-presheaf
![]() $\mathsf {\mathcal {T}\text{-}Mod}$
.)
$\mathsf {\mathcal {T}\text{-}Mod}$
.)
Proof This is again standard (see [Reference Johnstone17, Theorem D1.4.7], [Reference Makkai and Reyes23, Proposition 8.2.4]). The above functor is clearly faithful. For fullness, given
![]() $\kappa $
-continuous
$\kappa $
-continuous
![]() $\kappa $
-subextensive
$\kappa $
-subextensive
![]() $\mathcal {F}, \mathcal {G} : {\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle } \to \mathsf {C} \in \kappa \mathfrak {LimBSExtCat}$
and a
$\mathcal {F}, \mathcal {G} : {\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle } \to \mathsf {C} \in \kappa \mathfrak {LimBSExtCat}$
and a
![]() $\mathcal {T}$
-aqf embedding
$\mathcal {T}$
-aqf embedding
![]() $f : \mathcal {F}(\mathcal {H}) \to \mathcal {G}(\mathcal {H})$
, for each
$f : \mathcal {F}(\mathcal {H}) \to \mathcal {G}(\mathcal {H})$
, for each
![]() $\alpha \in \mathcal {L}_{\kappa \kappa }^{\mathcal {T}\mathrm {-aqf}}(X)$
, define
$\alpha \in \mathcal {L}_{\kappa \kappa }^{\mathcal {T}\mathrm {-aqf}}(X)$
, define
![]() $\xi _{(X, \alpha )} : \mathcal {F}(X, \alpha ) = \mathcal {F}(\alpha ^{\mathcal {H}}) = \alpha ^{\mathcal {F}(\mathcal {H})} \to \alpha ^{\mathcal {G}(\mathcal {H})} = \mathcal {G}(\alpha ^{\mathcal {M}}) = \mathcal {G}(X, \alpha )$
to be the restriction of
$\xi _{(X, \alpha )} : \mathcal {F}(X, \alpha ) = \mathcal {F}(\alpha ^{\mathcal {H}}) = \alpha ^{\mathcal {F}(\mathcal {H})} \to \alpha ^{\mathcal {G}(\mathcal {H})} = \mathcal {G}(\alpha ^{\mathcal {M}}) = \mathcal {G}(X, \alpha )$
to be the restriction of
![]() $f^X : \mathcal {F}(H)^X \to \mathcal {G}(H)^X$
(using that f is a
$f^X : \mathcal {F}(H)^X \to \mathcal {G}(H)^X$
(using that f is a
![]() $\mathcal {T}$
-aqf embedding). These form the components of a natural transformation
$\mathcal {T}$
-aqf embedding). These form the components of a natural transformation
![]() $\xi : \mathcal {F} \to \mathcal {G}$
: naturality with respect to the product projections
$\xi : \mathcal {F} \to \mathcal {G}$
: naturality with respect to the product projections
![]() $H^X = (X, \top ) \to (1, \top ) = H$
and the canonical inclusions
$H^X = (X, \top ) \to (1, \top ) = H$
and the canonical inclusions
![]() $(X, \alpha ) \hookrightarrow (X, \top ) = H^X$
is by definition; this implies naturality with respect to an arbitrary
$(X, \alpha ) \hookrightarrow (X, \top ) = H^X$
is by definition; this implies naturality with respect to an arbitrary
![]() $[\phi ] : (X, \alpha ) \to (Y, \beta ) \in {\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle }$
, by considering the factorization of
$[\phi ] : (X, \alpha ) \to (Y, \beta ) \in {\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle }$
, by considering the factorization of
![]() $[\phi ]$
through its graph
$[\phi ]$
through its graph
![]() $(X \sqcup Y, \phi )$
:
$(X \sqcup Y, \phi )$
:

For essential surjectivity, given a model
![]() $\mathcal {M} \in \mathsf {\mathcal {T}\text{-}Mod}(\mathsf {C})$
, define
$\mathcal {M} \in \mathsf {\mathcal {T}\text{-}Mod}(\mathsf {C})$
, define
![]() $\mathcal {F} : {\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle } \to \mathsf {C}$
by sending each object
$\mathcal {F} : {\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle } \to \mathsf {C}$
by sending each object
![]() $(X, \alpha )$
to (the domain of any monomorphism representative of the subobject)
$(X, \alpha )$
to (the domain of any monomorphism representative of the subobject)
![]() $\alpha ^{\mathcal {M}} \subseteq M^X$
, and each morphism
$\alpha ^{\mathcal {M}} \subseteq M^X$
, and each morphism
![]() $[\phi ] : (X, \alpha ) \to (Y, \beta )$
to the unique
$[\phi ] : (X, \alpha ) \to (Y, \beta )$
to the unique
![]() $\alpha ^{\mathcal {M}} \to \beta ^{\mathcal {M}} \in \mathsf {C}$
whose graph is
$\alpha ^{\mathcal {M}} \to \beta ^{\mathcal {M}} \in \mathsf {C}$
whose graph is
![]() $\phi ^{\mathcal {M}} \subseteq \alpha ^{\mathcal {M}} \times \beta ^{\mathcal {M}} \subseteq M^X \times M^Y = M^{X \sqcup Y}$
; it is straightforward to check, using the explicit constructions in Proposition 5.1, that
$\phi ^{\mathcal {M}} \subseteq \alpha ^{\mathcal {M}} \times \beta ^{\mathcal {M}} \subseteq M^X \times M^Y = M^{X \sqcup Y}$
; it is straightforward to check, using the explicit constructions in Proposition 5.1, that
![]() $\mathcal {F}$
is a
$\mathcal {F}$
is a
![]() $\kappa $
-continuous
$\kappa $
-continuous
![]() $\kappa $
-subextensive functor such that
$\kappa $
-subextensive functor such that
![]() $\mathcal {F}(\mathcal {H}) \cong \mathcal {M}$
.
$\mathcal {F}(\mathcal {H}) \cong \mathcal {M}$
.
5.3 The theory of 2
Let
![]() $\mathcal {L}_2$
be the language with a single unary relation symbol
$\mathcal {L}_2$
be the language with a single unary relation symbol
![]() $R_{\top } \in \mathcal {L}_2(1)$
. Let
$R_{\top } \in \mathcal {L}_2(1)$
. Let
![]() $\mathcal {T}_2$
be the
$\mathcal {T}_2$
be the
![]() $(\mathcal {L}_2)_{\kappa \kappa }$
-theory consisting of the sequents (where
$(\mathcal {L}_2)_{\kappa \kappa }$
-theory consisting of the sequents (where
![]() $x, y$
are distinct variables)
$x, y$
are distinct variables)
 $$ \begin{align*} &(\forall \{x, y\}) & (R_{\top}(x) \wedge R_{\top}(y) &\Rightarrow (x = y)), \\ &(\forall \{x, y\}) & (\neg R_{\top}(x) \wedge \neg R_{\top}(y) &\Rightarrow (x = y)), \\ &(\forall \emptyset) & (\top &\Rightarrow (\exists x) R_{\top}(x)), \\ &(\forall \emptyset) & (\top &\Rightarrow (\exists x) \neg R_{\top}(x) ). \end{align*} $$
$$ \begin{align*} &(\forall \{x, y\}) & (R_{\top}(x) \wedge R_{\top}(y) &\Rightarrow (x = y)), \\ &(\forall \{x, y\}) & (\neg R_{\top}(x) \wedge \neg R_{\top}(y) &\Rightarrow (x = y)), \\ &(\forall \emptyset) & (\top &\Rightarrow (\exists x) R_{\top}(x)), \\ &(\forall \emptyset) & (\top &\Rightarrow (\exists x) \neg R_{\top}(x) ). \end{align*} $$
The last two sequents are aqf relative to the first two, whence
![]() $\mathcal {T}_2$
is almost universal. It is easily seen that a model
$\mathcal {T}_2$
is almost universal. It is easily seen that a model
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathcal {T}_2$
in
$\mathcal {T}_2$
in
![]() $\mathsf {C} \in \kappa \mathfrak {LimBSExtCat}$
consists of an object
$\mathsf {C} \in \kappa \mathfrak {LimBSExtCat}$
consists of an object
![]() $M \in \mathsf {C}$
together with a subobject
$M \in \mathsf {C}$
together with a subobject
![]() $R_{\top }^{\mathcal {M}} \subseteq M$
which is a terminal object and whose complement is also a terminal object; in other words,
$R_{\top }^{\mathcal {M}} \subseteq M$
which is a terminal object and whose complement is also a terminal object; in other words,
Proposition 5.5. For any
![]() $\kappa $
-complete Boolean
$\kappa $
-complete Boolean
![]() $\kappa $
-subextensive category
$\kappa $
-subextensive category
![]() $\mathsf {C}$
,
$\mathsf {C}$
,
![]() $\mathsf {\mathcal {T}_2\text{-}Mod}(\mathsf {C})$
is the category of binary coproducts
$\mathsf {\mathcal {T}_2\text{-}Mod}(\mathsf {C})$
is the category of binary coproducts
![]() $1 \sqcup 1$
(equipped with cocone
$1 \sqcup 1$
(equipped with cocone
![]() $u, v : 1 \to 1 \sqcup 1$
) of the terminal object
$u, v : 1 \to 1 \sqcup 1$
) of the terminal object
![]() $1 \in \mathsf {C}$
.
$1 \in \mathsf {C}$
.
Corollary 5.6. If
![]() $\mathsf {C}$
is extensive, then
$\mathsf {C}$
is extensive, then
![]() $\mathsf {\mathcal {T}_2\text{-}Mod}(\mathsf {C})$
is equivalent to the terminal category.
$\mathsf {\mathcal {T}_2\text{-}Mod}(\mathsf {C})$
is equivalent to the terminal category.
Now take
![]() $\mathsf {C} := \kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
(which is
$\mathsf {C} := \kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
(which is
![]() $\kappa $
-complete Boolean
$\kappa $
-complete Boolean
![]() $\kappa $
-extensive by Corollary 3.9). By Corollary 3.4, we may identify subobjects of
$\kappa $
-extensive by Corollary 3.9). By Corollary 3.4, we may identify subobjects of
![]() $A \in \kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
with their elements
$A \in \kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
with their elements
![]() $a \in A$
. The binary coproduct of the terminal object in
$a \in A$
. The binary coproduct of the terminal object in
![]() $\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
is the binary product of the initial
$\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
is the binary product of the initial
![]() $\kappa $
-Boolean algebra
$\kappa $
-Boolean algebra
![]() $2 = \{\bot , \top \} \in \kappa \mathsf {Bool}_{\kappa }$
, which is the free algebra
$2 = \{\bot , \top \} \in \kappa \mathsf {Bool}_{\kappa }$
, which is the free algebra
![]() $\mathcal {K}(1) = \{\bot , 0, \neg 0, \top \}$
on one generator
$\mathcal {K}(1) = \{\bot , 0, \neg 0, \top \}$
on one generator
![]() $0 \in \mathcal {K}(1)$
; the two product projections
$0 \in \mathcal {K}(1)$
; the two product projections
![]() $\mathcal {K}(1) \twoheadrightarrow 2 \in \kappa \mathsf {Bool}_{\kappa }$
take
$\mathcal {K}(1) \twoheadrightarrow 2 \in \kappa \mathsf {Bool}_{\kappa }$
take
![]() $0$
to
$0$
to
![]() $\top $
and
$\top $
and
![]() $\bot $
respectively, which, when seen as subobjects of
$\bot $
respectively, which, when seen as subobjects of
![]() $\mathcal {K}(1)$
in
$\mathcal {K}(1)$
in
![]() $\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
, correspond via Corollary 3.4 to the elements
$\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
, correspond via Corollary 3.4 to the elements
![]() $0, \neg 0 \in \mathcal {K}(1)$
. Thus, the model
$0, \neg 0 \in \mathcal {K}(1)$
. Thus, the model
![]() $\mathcal {M}_2 \in \mathsf {\mathcal {T}_2\text{-}Mod}(\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}})$
given by Corollary 5.6 may be taken as (again using Corollary 3.4)
$\mathcal {M}_2 \in \mathsf {\mathcal {T}_2\text{-}Mod}(\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}})$
given by Corollary 5.6 may be taken as (again using Corollary 3.4)
Theorem 5.7 (
 $\mathcal {T}_2$
presents
$\mathcal {T}_2$
presents
 $\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
)
$\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
)
The
![]() $\kappa $
-continuous subextensive functor
$\kappa $
-continuous subextensive functor
![]() $\mathcal {F}_2 : {\langle }{\mathcal {L}_2 \mid \mathcal {T}_2}{\rangle } \to \kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
corresponding to
$\mathcal {F}_2 : {\langle }{\mathcal {L}_2 \mid \mathcal {T}_2}{\rangle } \to \kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
corresponding to
![]() $\mathcal {M}_2$
via Proposition 5.4 is an equivalence of categories.
$\mathcal {M}_2$
via Proposition 5.4 is an equivalence of categories.
Proof Since
![]() $\mathcal {F}_2$
takes the universal model
$\mathcal {F}_2$
takes the universal model
![]() $\mathcal {H} = ((1, \top ), (1, R_{\top }(0)))$
to an isomorphic copy of
$\mathcal {H} = ((1, \top ), (1, R_{\top }(0)))$
to an isomorphic copy of
![]() $\mathcal {M}_2 = (\mathcal {K}(1), 0)$
, we may assume that
$\mathcal {M}_2 = (\mathcal {K}(1), 0)$
, we may assume that
![]() $\mathcal {F}_2(1, \top ) = \mathcal {K}(1)$
and
$\mathcal {F}_2(1, \top ) = \mathcal {K}(1)$
and
![]() $\mathcal {F}_2(1, R_{\top }(0)) = 0 \in \mathcal {K}(1)$
(again identifying subobjects in
$\mathcal {F}_2(1, R_{\top }(0)) = 0 \in \mathcal {K}(1)$
(again identifying subobjects in
![]() $\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
with elements using Corollary 3.4). Since
$\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
with elements using Corollary 3.4). Since
![]() $\mathcal {F}_2$
preserves
$\mathcal {F}_2$
preserves
![]() $\kappa $
-ary products, we may further assume that
$\kappa $
-ary products, we may further assume that
![]() $\mathcal {F}_2(X, \top ) = \mathcal {F}_2((1, \top )^X) = \mathcal {K}(1)^X = \mathcal {K}(X) \in \kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
for each
$\mathcal {F}_2(X, \top ) = \mathcal {F}_2((1, \top )^X) = \mathcal {K}(1)^X = \mathcal {K}(X) \in \kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
for each
![]() $X \in \mathsf {Set}^{\prime }_{\kappa }$
, and that
$X \in \mathsf {Set}^{\prime }_{\kappa }$
, and that
![]() $\mathcal {F}_2$
takes the product projections
$\mathcal {F}_2$
takes the product projections
![]() $\pi _x : (X, \top ) \to (1, \top ) \in {\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle }$
to the corresponding projections in
$\pi _x : (X, \top ) \to (1, \top ) \in {\langle }{\mathcal {L} \mid \mathcal {T}}{\rangle }$
to the corresponding projections in
![]() $\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
, i.e., the coproduct injections
$\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
, i.e., the coproduct injections
![]() $\mathcal {K}(x) : \mathcal {K}(1) \to \mathcal {K}(X) \in \kappa \mathsf {Bool}_{\kappa }$
taking the generator
$\mathcal {K}(x) : \mathcal {K}(1) \to \mathcal {K}(X) \in \kappa \mathsf {Bool}_{\kappa }$
taking the generator
![]() $0 \in \mathcal {K}(1)$
to
$0 \in \mathcal {K}(1)$
to
![]() $x \in \mathcal {K}(X)$
.
$x \in \mathcal {K}(X)$
.
Let us say that a formula
![]() $\phi \in (\mathcal {L}_2)_{\kappa \kappa }(X)$
is quantifier-and-equality-free (qef) if it contains neither quantifiers nor
$\phi \in (\mathcal {L}_2)_{\kappa \kappa }(X)$
is quantifier-and-equality-free (qef) if it contains neither quantifiers nor
![]() $=$
. In particular, such a formula is
$=$
. In particular, such a formula is
![]() $\mathcal {T}_2$
-aqf (indeed
$\mathcal {T}_2$
-aqf (indeed
![]() $\emptyset $
-aqf). Note that such a formula is essentially a
$\emptyset $
-aqf). Note that such a formula is essentially a
![]() $\kappa $
-Boolean algebra term in the generators X, except with each generator
$\kappa $
-Boolean algebra term in the generators X, except with each generator
![]() $x \in X$
replaced by the atomic formula
$x \in X$
replaced by the atomic formula
![]() $R_{\top }(x)$
. For each such atomic formula, the corresponding subobject
$R_{\top }(x)$
. For each such atomic formula, the corresponding subobject
![]() $(X, R_{\top }(x)) \subseteq (X, \top ) \in {\langle }{\mathcal {L}_2 \mid \mathcal {T}_2}{\rangle }$
is (by Proposition 5.1) the pullback along the projection
$(X, R_{\top }(x)) \subseteq (X, \top ) \in {\langle }{\mathcal {L}_2 \mid \mathcal {T}_2}{\rangle }$
is (by Proposition 5.1) the pullback along the projection
![]() $\pi _x : (X, \top ) \to (1, \top )$
of
$\pi _x : (X, \top ) \to (1, \top )$
of
![]() $(1, R_{\top }(0)) \subseteq (1, \top )$
; since
$(1, R_{\top }(0)) \subseteq (1, \top )$
; since
![]() $\mathcal {F}_2$
preserves pullbacks,
$\mathcal {F}_2$
preserves pullbacks,
![]() $\mathcal {F}_2(X, R_{\top }(x)) \subseteq \mathcal {F}_2(X, \top ) = \mathcal {K}(X) \in \kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
must be the pushout in
$\mathcal {F}_2(X, R_{\top }(x)) \subseteq \mathcal {F}_2(X, \top ) = \mathcal {K}(X) \in \kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
must be the pushout in
![]() $\kappa \mathsf {Bool}_{\kappa }$
of the quotient
$\kappa \mathsf {Bool}_{\kappa }$
of the quotient
![]() $\mathcal {K}(1) \twoheadrightarrow \mathcal {K}(1)/0$
along
$\mathcal {K}(1) \twoheadrightarrow \mathcal {K}(1)/0$
along
![]() $\iota _x : \mathcal {K}(1) \to \mathcal {K}(X)$
, which is the quotient
$\iota _x : \mathcal {K}(1) \to \mathcal {K}(X)$
, which is the quotient
![]() $\mathcal {K}(X) \twoheadrightarrow \mathcal {K}(X)/x$
, i.e., the subobject (via Corollary 3.4)
$\mathcal {K}(X) \twoheadrightarrow \mathcal {K}(X)/x$
, i.e., the subobject (via Corollary 3.4)
![]() $x \in \mathcal {K}(X)$
. So for each
$x \in \mathcal {K}(X)$
. So for each
![]() $(X, \top ) \in {\langle }{\mathcal {L}_2 \mid \mathcal {T}_2}{\rangle }$
, the
$(X, \top ) \in {\langle }{\mathcal {L}_2 \mid \mathcal {T}_2}{\rangle }$
, the
![]() $\kappa $
-Boolean homomorphism
$\kappa $
-Boolean homomorphism

(the first
![]() $\cong $
by Proposition 5.1) maps
$\cong $
by Proposition 5.1) maps
By freeness of
![]() $\mathcal {K}(X)$
,
$\mathcal {K}(X)$
,
![]() $r_X$
has a section
$r_X$
has a section

whose image clearly consists of the equivalence classes of qef formulas. Also, clearly, the
![]() $s_X$
form a natural transformation
$s_X$
form a natural transformation
![]() $\mathcal {K} \to (\mathcal {L}_2)_{\kappa \kappa }^{\mathcal {T}_2\mathrm {-aqf}}/\mathcal {T}_2 : \mathsf {Set}^{\prime }_{\kappa } \to \kappa \mathsf {Bool}$
, i.e., for any
$\mathcal {K} \to (\mathcal {L}_2)_{\kappa \kappa }^{\mathcal {T}_2\mathrm {-aqf}}/\mathcal {T}_2 : \mathsf {Set}^{\prime }_{\kappa } \to \kappa \mathsf {Bool}$
, i.e., for any
![]() $f : X \to Y \in \mathsf {Set}^{\prime }_{\kappa }$
,
$f : X \to Y \in \mathsf {Set}^{\prime }_{\kappa }$
,
(this clearly holds on generators
![]() $a = x \in X$
); it follows that
$a = x \in X$
); it follows that
(since
![]() $[\phi ] \in \mathrm {im}(s_X)$
, so
$[\phi ] \in \mathrm {im}(s_X)$
, so
![]() $r_Y([f][\phi ]) = r_Y([f]s_X(r_X[\phi ])) = r_Y(s_Y(f_*(r_X[\phi ]))) = f_*(r_X[\phi ])$
).
$r_Y([f][\phi ]) = r_Y([f]s_X(r_X[\phi ])) = r_Y(s_Y(f_*(r_X[\phi ]))) = f_*(r_X[\phi ])$
).
Lemma 5.8 (Quantifier and equality elimination for
 $\mathcal {T}_2$
)
$\mathcal {T}_2$
)
Every
![]() $\phi \in (\mathcal {L}_2)_{\kappa \kappa }^{\mathcal {T}_2\mathrm {-aqf}}(X)$
is
$\phi \in (\mathcal {L}_2)_{\kappa \kappa }^{\mathcal {T}_2\mathrm {-aqf}}(X)$
is
![]() $\mathcal {T}_2$
-provably equivalent to a qef formula. Thus, the homomorphisms
$\mathcal {T}_2$
-provably equivalent to a qef formula. Thus, the homomorphisms
![]() $r_X, s_X$
above are inverse isomorphisms.
$r_X, s_X$
above are inverse isomorphisms.
Proof An equality
![]() $(x = y)$
is easily
$(x = y)$
is easily
![]() $\mathcal {T}_2$
-equivalent to the qef formula
$\mathcal {T}_2$
-equivalent to the qef formula
![]() $R_{\top }(x) \leftrightarrow R_{\top }(y)$
. Thus by induction, it is enough to prove that for any qef
$R_{\top }(x) \leftrightarrow R_{\top }(y)$
. Thus by induction, it is enough to prove that for any qef
![]() $\phi \in (\mathcal {L}_2)_{\kappa \kappa }(X)$
and
$\phi \in (\mathcal {L}_2)_{\kappa \kappa }(X)$
and
![]() $X = Y \sqcup Z$
, if the existential
$X = Y \sqcup Z$
, if the existential
![]() $(\exists Y) \phi \in (\mathcal {L}_2)_{\kappa \kappa }(Z)$
is
$(\exists Y) \phi \in (\mathcal {L}_2)_{\kappa \kappa }(Z)$
is
![]() $\mathcal {T}_2$
-provably unique, then it is
$\mathcal {T}_2$
-provably unique, then it is
![]() $\mathcal {T}_2$
-equivalent to a qef formula.
$\mathcal {T}_2$
-equivalent to a qef formula.
That
![]() $(\exists Y) \phi $
is
$(\exists Y) \phi $
is
![]() $\mathcal {T}_2$
-provably unique means
$\mathcal {T}_2$
-provably unique means
 $$ \begin{align*} \mathcal{T}_2 \vdash (\forall X \sqcup Y') \left([f]\phi \wedge [g]\phi \Rightarrow \bigwedge\nolimits_{y \in Y} (f(y) = g(y))\right), \end{align*} $$
$$ \begin{align*} \mathcal{T}_2 \vdash (\forall X \sqcup Y') \left([f]\phi \wedge [g]\phi \Rightarrow \bigwedge\nolimits_{y \in Y} (f(y) = g(y))\right), \end{align*} $$
where
![]() $Y'$
is a copy of Y disjoint from X, with bijection
$Y'$
is a copy of Y disjoint from X, with bijection
![]() $g : Y \cong Y'$
extending to
$g : Y \cong Y'$
extending to
![]() $g : X = Y \sqcup Z \cong Y' \sqcup Z \subseteq X \sqcup Y'$
, and
$g : X = Y \sqcup Z \cong Y' \sqcup Z \subseteq X \sqcup Y'$
, and
![]() $f : X \hookrightarrow X \sqcup Y'$
is the inclusion. Eliminating the equalities
$f : X \hookrightarrow X \sqcup Y'$
is the inclusion. Eliminating the equalities
![]() $f(y) = g(y)$
as above yields
$f(y) = g(y)$
as above yields
 $$ \begin{align*} \mathcal{T}_2 \vdash (\forall X \sqcup Y') \left([f]\phi \wedge [g]\phi \Rightarrow \bigwedge\nolimits_{y \in Y} (R_{\top}(f(y)) \leftrightarrow R_{\top}(g(y)))\right), \end{align*} $$
$$ \begin{align*} \mathcal{T}_2 \vdash (\forall X \sqcup Y') \left([f]\phi \wedge [g]\phi \Rightarrow \bigwedge\nolimits_{y \in Y} (R_{\top}(f(y)) \leftrightarrow R_{\top}(g(y)))\right), \end{align*} $$
i.e.,
Applying
![]() $r_{X \sqcup Y'}$
and (
$r_{X \sqcup Y'}$
and (
![]() $\dagger $
) yields
$\dagger $
) yields
By Lemma 3.5, there is a retraction
![]() $h : \mathcal {K}(X) \twoheadrightarrow \mathcal {K}(Z) \in \kappa \mathsf {Bool}_{\kappa }$
of
$h : \mathcal {K}(X) \twoheadrightarrow \mathcal {K}(Z) \in \kappa \mathsf {Bool}_{\kappa }$
of
![]() $i_*$
, where
$i_*$
, where
![]() $i : Z \hookrightarrow X$
is the inclusion, such that
$i : Z \hookrightarrow X$
is the inclusion, such that
Applying
![]() $s_X$
and (
$s_X$
and (
![]() $*$
) yields
$*$
) yields
So letting
![]() $s_X(h(r_X[\phi ])) = [\psi ]$
and
$s_X(h(r_X[\phi ])) = [\psi ]$
and
![]() $s_X(h(y)) = [\psi _y]$
for some qef
$s_X(h(y)) = [\psi _y]$
for some qef
![]() $\psi , \psi _y \in (\mathcal {L}_2)_{\kappa \kappa }(Z)$
, we have
$\psi , \psi _y \in (\mathcal {L}_2)_{\kappa \kappa }(Z)$
, we have
 $$ \begin{align*} \mathcal{T}_2 \vdash (\forall X) \left(\phi \Leftrightarrow \psi \wedge \bigwedge\nolimits_{y \in Y} (\psi_i \leftrightarrow R_{\top}(y))\right). \end{align*} $$
$$ \begin{align*} \mathcal{T}_2 \vdash (\forall X) \left(\phi \Leftrightarrow \psi \wedge \bigwedge\nolimits_{y \in Y} (\psi_i \leftrightarrow R_{\top}(y))\right). \end{align*} $$
This easily yields
 $$ \begin{align*} \mathcal{T}_2 \vdash (\forall Z) \left((\exists Y) \phi \Leftrightarrow \psi \wedge (\exists Y) \bigwedge\nolimits_{y \in Y} (\psi_i \leftrightarrow R_{\top}(y))\right), \end{align*} $$
$$ \begin{align*} \mathcal{T}_2 \vdash (\forall Z) \left((\exists Y) \phi \Leftrightarrow \psi \wedge (\exists Y) \bigwedge\nolimits_{y \in Y} (\psi_i \leftrightarrow R_{\top}(y))\right), \end{align*} $$
where
![]() $(\exists Y) \bigwedge\nolimits_{y \in Y} (\psi _i \leftrightarrow R_{\top }(y))$
is
$(\exists Y) \bigwedge\nolimits_{y \in Y} (\psi _i \leftrightarrow R_{\top }(y))$
is
![]() $\mathcal {T}_2$
-provably unique by the first two axioms of
$\mathcal {T}_2$
-provably unique by the first two axioms of
![]() $\mathcal {T}_2$
; but then the last two axioms of
$\mathcal {T}_2$
; but then the last two axioms of
![]() $\mathcal {T}_2$
easily prove
$\mathcal {T}_2$
easily prove
![]() $\bigwedge\nolimits_{y \in Y} (\exists y) (\psi _i \leftrightarrow R_{\top }(y))$
, which implies
$\bigwedge\nolimits_{y \in Y} (\exists y) (\psi _i \leftrightarrow R_{\top }(y))$
, which implies
![]() $(\exists Y) \bigwedge\nolimits_{y \in Y} (\psi _i \leftrightarrow R_{\top }(y))$
by (AC). So
$(\exists Y) \bigwedge\nolimits_{y \in Y} (\psi _i \leftrightarrow R_{\top }(y))$
by (AC). So
![]() $\mathcal {T}_2 \vdash (\forall Z) ((\exists Y) \phi \Leftrightarrow \psi )$
.
$\mathcal {T}_2 \vdash (\forall Z) ((\exists Y) \phi \Leftrightarrow \psi )$
.
So
![]() $\mathcal {F}_2 : {\langle }{\mathcal {L}_2 \mid \mathcal {T}_2}{\rangle } \to \kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
is an isomorphism on each subobject poset
$\mathcal {F}_2 : {\langle }{\mathcal {L}_2 \mid \mathcal {T}_2}{\rangle } \to \kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
is an isomorphism on each subobject poset
![]() $\mathrm {Sub}_{{\langle }{\mathcal {L}_2 \mid \mathcal {T}_2}{\rangle }}(X, \top )$
. It follows easily that it restricts to an isomorphism on every subobject poset
$\mathrm {Sub}_{{\langle }{\mathcal {L}_2 \mid \mathcal {T}_2}{\rangle }}(X, \top )$
. It follows easily that it restricts to an isomorphism on every subobject poset
![]() $\mathrm {Sub}_{{\langle }{\mathcal {L}_2 \mid \mathcal {T}_2}{\rangle }}(X, \alpha )$
, where we may assume
$\mathrm {Sub}_{{\langle }{\mathcal {L}_2 \mid \mathcal {T}_2}{\rangle }}(X, \alpha )$
, where we may assume
![]() $\alpha $
is qef by Lemma 5.8, by considering the commutative diagram
$\alpha $
is qef by Lemma 5.8, by considering the commutative diagram

where the vertical arrows are inclusions (note: not
![]() $\kappa $
-Boolean homomorphisms): injectivity of
$\kappa $
-Boolean homomorphisms): injectivity of
![]() $\mathcal {F}_2|\mathrm {Sub}(X, \alpha )$
follows immediately from that of
$\mathcal {F}_2|\mathrm {Sub}(X, \alpha )$
follows immediately from that of
![]() $\mathcal {F}_2|\mathrm {Sub}(X, \top )$
; for surjectivity, for
$\mathcal {F}_2|\mathrm {Sub}(X, \top )$
; for surjectivity, for
![]() $b \in {\downarrow } r_X[\alpha ]$
, letting
$b \in {\downarrow } r_X[\alpha ]$
, letting
![]() $\beta \in (\mathcal {L}_2)_{\kappa \kappa }(X)$
be qef with
$\beta \in (\mathcal {L}_2)_{\kappa \kappa }(X)$
be qef with
![]() $[\beta ] = s_X(b) \le s_X(r_X[\alpha ]) = [\alpha ]$
, we have
$[\beta ] = s_X(b) \le s_X(r_X[\alpha ]) = [\alpha ]$
, we have
![]() $(X, \beta ) \in \mathrm {Sub}(X, \alpha )$
with
$(X, \beta ) \in \mathrm {Sub}(X, \alpha )$
with
![]() $\mathcal {F}_2(X, \beta ) = r_X[\beta ] = r_X(s_X(b)) = b$
.
$\mathcal {F}_2(X, \beta ) = r_X[\beta ] = r_X(s_X(b)) = b$
.
Finally, every
![]() $A \in \kappa \mathsf {Bool}_{\kappa }$
is (up to isomorphism) a quotient of a free algebra
$A \in \kappa \mathsf {Bool}_{\kappa }$
is (up to isomorphism) a quotient of a free algebra
![]() $\mathcal {K}(X)$
for some
$\mathcal {K}(X)$
for some
![]() $X \in \mathsf {Set}^{\prime }_{\kappa }$
, i.e., a subobject in
$X \in \mathsf {Set}^{\prime }_{\kappa }$
, i.e., a subobject in
![]() $\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
of some
$\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
of some
![]() $\mathcal {K}(X) = \mathcal {F}_2(X, \top )$
; so
$\mathcal {K}(X) = \mathcal {F}_2(X, \top )$
; so
![]() $\mathcal {F}_2$
is essentially surjective. So
$\mathcal {F}_2$
is essentially surjective. So
![]() $\mathcal {F}_2$
is a finitely continuous functor between finitely complete categories which is a bijection on each subobject poset (in the usual terminology, conservative and full on subobjects) as well as essentially surjective, hence an equivalence (see, e.g., [Reference Johnstone17, Lemma D3.5.6]).
$\mathcal {F}_2$
is a finitely continuous functor between finitely complete categories which is a bijection on each subobject poset (in the usual terminology, conservative and full on subobjects) as well as essentially surjective, hence an equivalence (see, e.g., [Reference Johnstone17, Lemma D3.5.6]).
Theorem 5.9.
![]() $\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
is an initial object in
$\kappa \mathsf {Bool}_{\kappa }^{\mathrm {op}}$
is an initial object in
![]() $\kappa \mathfrak {LimBExtCat}$
.
$\kappa \mathfrak {LimBExtCat}$
.
Acknowledgment
I would like to thank Matthew de Brecht for some stimulating discussions that partly inspired this work, as well as the referee for some helpful corrections and suggestions.