Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2025-01-03T11:51:43.238Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniform inductive definability and infinitary languages

Published online by Cambridge University Press:  12 March 2014

Anders M. Nyberg
Anders M. Nyberg*
Affiliation:
University of Oslo, Oslo, Norway
Get access Rights & Permissions [Opens in a new window]

Extract

Introduction. The purpose of this paper is to show how results from the theory of inductive definitions can be used to obtain new compactness theorems for uncountable admissible languages. These will include improvements of the compactness theorem by J. Green [9].

In [2] Barwise studies admissible sets satisfying the Σ1-compactness theorem. Our approach is to consider admissible sets satisfying what could be called the abstract extended completeness theorem, that is, sets where the consequence relation of the admissible fragment LA is Σ1-definable over A. We will call such sets Σ1-complete. For countable admissible sets, Σ1-completeness follows from the completeness theorem for LA .

Having restricted our attention to Σ1-complete sets we are led to a stronger notion also true on countable admissible sets, namely what we shall call uniform Σ1-completeness. We will see that this notion can be viewed as extending to uncountable admissible sets, properties related to both the “recursion theory” and “proof theory” of countable admissible sets.

By following Barwise's recent approach to admissible sets allowing “urelements,” we show that there is a natural connection between certain structures 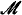arising from the theory of inductive definability, and uniformly Σ1-complete admissible sets 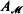. The structures we have in mind are called uniform Kleene structures.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 41 , Issue 1 , March 1976 , pp. 109 - 120
Copyright
Copyright © Association for Symbolic Logic 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

The research for this paper was done while the author was a visitor of the University of Wisconsin, Madison, and Oxford University, England, with financial support from the University of Oslo and the Norwegian Research Council for Science and the Humanities (NAVF). The author is greatly indebted to K. J. Barwise for his encouragement and interest during the preparation of this paper.

References

REFERENCES

[1] Barwise, J. Infinitary logic and admissible sets, this Journal, vol. 34 (1969), pp. 226–252.Google Scholar
[2] Barwise, J. Applications of strict Π1 1 predicates to infinitary logic, this Journal, vol. 34 (1969), pp. 409–423.Google Scholar
[3] Barwise, J. Admissible sets over models of set theory, Generalized recursion theory (Oslo, 1972) (Fenstad, J. E. and Hinman, P., Editors), North-Holland, Amsterdam, 1973.Google Scholar
[4] Barwise, J. Admissible sets and structures, Perspectives on mathematical logic, Springer-Verlag, Berlin and New York, 1975.Google Scholar
[B.G.M.] Barwise, J., Gandy, R., Moschovakis, Y. The next admissible set, this Journal, vol. 36 (1971), pp. 108–120.Google Scholar
[6] Chang, C. C., Moschovakis, Y. The Suslin-Kleene theorem for Vκ with cofinality (κ) = ω, Pacific Journal of Mathematics, vol. 35 (1970), pp. 565–569.CrossRefGoogle Scholar
[7] Friedman, H., Jensen, R. Note on admissible ordinals. The syntax and semantics of infinitary languages, Springer lecture notes, no. 72, 1968.Google Scholar
[8] Gandy, R. Inductive definitions, Generalized recursion theory (Oslo, 1972) (Fenstad, J. E. and Hinman, P., Editors), North-Holland, Amsterdam, 1973.Google Scholar
[9] Green, J. Σ1 compactness for next admissible sets, Preprint.Google Scholar
[10] Kleene, S. C. Hierarchies of number-theoretic predicates, Bulletin of the American Mathematical Society, vol. 61 (1955), pp. 193–213.CrossRefGoogle Scholar
[11] Kleene, S. C. Recursive functionals and quantifiers of finite types. I, Transactions of the American Mathematical Society, vol. 91 (1959), pp. 1–52.Google Scholar
[12] Kreisel, G. Choice of infinitary languages by means of definability criteria; Generalized recursion theory, Springer lecture notes, no. 72, 1968.Google Scholar
[13] Kunen, K. Implicit definability and infinitary languages, this Journal, vol. 33 (1968), pp. 446–451.Google Scholar
[14] Makkai, M. Generalizing Vaught sentences from ω to strong cofinality ω, Preprint.Google Scholar
[15] Moschovakis, Y. The Suslin-Kleene theorem for countable structures, Duke Mathematical Journal, vol. 37 (1970), pp. 341–352.CrossRefGoogle Scholar
[16] Moschovakis, Y. Elementary inductions on abstract structures, North-Holland, Amsterdam, 1973.Google Scholar
[17] Nyberg, A. M. Applications of model theory to recursion theory on structures of strong cofinality ω, Pre-print Series, Institute of Mathematics, University of Oslo, no. 17, 1974.Google Scholar
[18] Spector, C. Inductively defined sets of natural numbers, Infinitistic Methods, Warsaw, 1961, pp. 97–102.Google Scholar