Published online by Cambridge University Press: 05 October 2020
We prove first-order definability of the prime subring inside polynomial rings, whose coefficient rings are (commutative unital) reduced and indecomposable. This is achieved by means of a uniform formula in the language of rings with signature 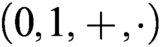 $(0,1,+,\cdot )$. In the characteristic zero case, the claim implies that the full theory is undecidable, for rings of the referred type. This extends a series of results by Raphael Robinson, holding for certain polynomial integral domains, to a more general class.
$(0,1,+,\cdot )$. In the characteristic zero case, the claim implies that the full theory is undecidable, for rings of the referred type. This extends a series of results by Raphael Robinson, holding for certain polynomial integral domains, to a more general class.