Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-16T15:19:25.938Z Has data issue: false hasContentIssue false
  • English
  • Français

UNDECIDABILITY OF THE FIRST ORDER THEORIES OF FREE NONCOMMUTATIVE LIE ALGEBRAS

Published online by Cambridge University Press:  23 October 2018

OLGA KHARLAMPOVICH  and
ALEXEI MYASNIKOV
OLGA KHARLAMPOVICH
Affiliation:
DEPARTMENT OF MATHEMATICS AND STATISTICS HUNTER COLLEGE, CUNY NEW YORK, NY 10065, USAE-mail: [email protected]
ALEXEI MYASNIKOV
Affiliation:
DEPARTMENT OF MATHEMATICAL SCIENCES STEVENS INSTITUTE OF TECHNOLOGY HOBOKEN, NJ 07030, USAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let R be a commutative integral unital domain and L a free noncommutative Lie algebra over R. In this article we show that the ring R and its action on L are 0-interpretable in L, viewed as a ring with the standard ring language 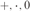$+ , \cdot ,0$. Furthermore, if R has characteristic zero then we prove that the elementary theory 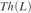$Th\left( L \right)$ of L in the standard ring language is undecidable. To do so we show that the arithmetic 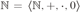${\Bbb N} = \langle {\Bbb N}, + , \cdot ,0\rangle $ is 0-interpretable in L. This implies that the theory of 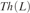$Th\left( L \right)$ has the independence property. These results answer some old questions on model theory of free Lie algebras.

Keywords

03C60Lie algebraelementary theory
Type
Articles
Information
The Journal of Symbolic Logic , Volume 83 , Issue 3 , September 2018 , pp. 1204 - 1216
Copyright
Copyright © The Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bahturin, Y., Identical Relations in Lie Algebras, VNU Science Press, Moscow, 1987.Google Scholar
Baudisch, A., On elementary properties of free Lie algebras. Annals of Pure and Applied Logic, vol. 30 (1986), pp. 121–136.CrossRefGoogle Scholar
Bokut’, L. A. and Kukin, G. P., Algorithmic and Combinatorial Algebra, Mathematics and Its Applications, vol. 255, Springer, Dordrecht, 1994.CrossRefGoogle Scholar
Lavrov, I. A., Undecidability of elementary theories of some rings. Algebra i Logika, vol. 1 (1963), no. 3, pp. 39–45.Google Scholar
Jarden, M. and Lubotzky, A., Elementary equivalence of profinite groups. Bulletin of the London Mathematical Society, vol. 40 (2008), no. 5, pp. 887–896.CrossRefGoogle Scholar
Kharlampovich, O. and Myasnikov, A., Elementary theory of free nonabelian groups.Journal of Algebra, vol. 302 (2006), no. 2, pp. 451–552.CrossRefGoogle Scholar
Kharlampovich, O. and Myasnikov, A., Model theory and algebraic geometry in groups, nonstandard actions and algorithmic problems, Proceedings of the International Congress of Mathematicians, Invited Lectures, vol. 2, Kyung Moon Sa Co., Seoul, 2014, pp. 223–244.Google Scholar
Kharlampovich, O. and Myasnikov, A., Tarski-type problems for free associative algebras. Journal of Algebra, 2017. Available at https://doi.org/10.1016/j.jalgebra.2017.10.001.Google Scholar
Kharlampovich, O. and Myasnikov, A., Equations in algebras. To appear in the International Journal of Algebra and Computation. Preprint, 2016. arXiv:1606.03617.Google Scholar
Kharlampovich, O. and Myasnikov, A., First-order theory of group algebras. Preprint, 2016. arXiv:1509.04112.Google Scholar
Magnus, W., Karras, A., and Solitar, D., Combinatorial Group Theory, Dover, New York, 1976.Google Scholar
Myasnikov, A., Recursive p-adic numbers and elementary theories of finitely generated pro-p-groups. Mathematics of the USSR-Izvestiya, vol. 34 (1988), no. 3, pp. 577–597.CrossRefGoogle Scholar
Myasnikov, A., The structure of models and a criterion for the decidability of complete theories of finite-dimensional algebras. (Russian) Izvestiya Akademii Nauk SSSR, Seriya Matematicheskikh, vol. 53 (1989), no. 2, pp. 379–397; English translation in Mathematics of the USSR-Izvestiya, vol. 34 (1990), no. 2, pp. 389–407.Google Scholar
Myasnikov, A., Definable invariants of bilinear mappings. Siberian Mathematical Journal, vol. 31 (1990), no. 1, pp. 104–115.CrossRefGoogle Scholar
Sela, Z., Diophantine geometry over groups VI: The elementary theory of a free group. Geometric and Functional Analysis, vol. 16 (2006), pp. 707–730.Google Scholar