Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-22T21:15:50.340Z Has data issue: false hasContentIssue false
  • English
  • Français

Undecidability of modal and intermediate first-order logics with two individual variables

Published online by Cambridge University Press:  12 March 2014

D. M. Gabbay  and
V. B. Shehtman
D. M. Gabbay
Affiliation:
Department of Computing, Imperial College, London SW7 2BZ, E-mail: [email protected]
V. B. Shehtman
Affiliation:
Institute of New Technologies, Kirovogradskaya 11, Moscow 113587, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

The interest in fragments of predicate logics is motivated by the well-known fact that full classical predicate calculus is undecidable (cf. Church [1936]). So it is desirable to find decidable fragments which are in some sense “maximal”, i.e., which become undecidable if they are “slightly” extended. Or, alternatively, we can look for “minimal” undecidable fragments and try to identify the vague boundary between decidability and undecidability. A great deal of work in this area concerning mainly classical logic has been done since the thirties. We will not give a complete review of decidability and undecidability results in classical logic, referring the reader to existing monographs (cf. Suranyi [1959], Lewis [1979], and Dreben, Goldfarb [1979]). A short summary can also be found in the well-known book Church [1956]. Let us recall only several facts. Herein we will consider only logics without functional symbols, constants, and equality.

(C1) The fragment of the classical logic with only monadic predicate letters is decidable (cf. Behmann [1922]).

(C2) The fragment of the classical logic with a single binary predicate letter is undecidable. (This is a consequence of Gödel [1933].)

(C3) The fragment of the classical logic with a single individual variable is decidable; in fact it is equivalent to Lewis S5 (cf. Wajsberg [1933]).

(C4) The fragment of the classical logic with two individual variables is decidable (Segerberg [1973] contains a proof using modal logic; Scott [1962] and Mortimer [1975] give traditional proofs.)

(C5) The fragment of the classical logic with three individual variables and binary predicate letters is undecidable (cf. Surańyi [1943]). In fact this paper considers formulas of the following type

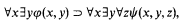
φ,ψ being quantifier-free and the set of binary predicate letters which can appear in φ or ψ being fixed and finite.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 58 , Issue 3 , September 1993 , pp. 800 - 823
Copyright
Copyright © Association for Symbolic Logic 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Artemov, S. and Dzhaparidze, G. [1990], Finite Kripke models and predicate logics of provability, this Journal, vol. 55, pp. 1090–1098.Google Scholar
Behmann, H. [1922], Beiträge zur Algebra der Logik, inbesondere zum Entscheidungsproblem, Mathematische Annalen, vol. 86, pp. 163–229.CrossRefGoogle Scholar
Church, A. [1936], A note on the “Entscheidungsproblem”, this Journal, vol. 1, pp. 40–41.Google Scholar
Church, A. [1956], Introduction to mathematical logic V. 1, Princeton University Press, Princeton, New Jersey, 1956.Google Scholar
Dreben, B. and Goldfarb, W. D. [1979], The decision problem. Solvable classes of quantificational formulas, Addison Wesley, Reading, Massachusetts.Google Scholar
Ehsakia, L. L. and Meskhi, V. Yu. [1977], Five critical modal systems, Theoria, vol. 43, pp. 52–60.CrossRefGoogle Scholar
Fischer-Servi, G. [1978], The finite model property for MIPQ and some consequences, Notre Dame Journal of Formal Logic, vol. 19, pp. 687–692.CrossRefGoogle Scholar
Gabbay, D. M. [1976], Investigations in modal and tense logics with implications to problems in philosophy and linguistics, Synthese Library, vol. 92, Reidel, Dordrecht.Google Scholar
Gabbay, D. M. [1981], Semantical investigations in Heyting's intuitionistic logic, Synthese Library, vol. 148, Reidel, Dordrecht.CrossRefGoogle Scholar
Gödel, K. [1933], Zum Entscheidungsproblem des logischen Funktionenkalküls, Monatschefte für Mathematische Physika, vol. 40, pp. 433–443.Google Scholar
Kahr, A. S., Moore, E. F., and Wahg, Hao [1962], Entscheidungsproblem reduced to the ∀∃∀ case, Proceedings of the National Academy of Science of the United States of America, vol. 48, pp. 365–377.CrossRefGoogle Scholar
Kripke, S. [1959], A completeness theorem in modal logic, this Journal, vol. 24, pp. 1–14.Google Scholar
Kripke, S. [1962], The undecidability of monadic modal quantificational theory, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 8 pp. 113–116.CrossRefGoogle Scholar
Kripke, S. [1965], Semantical analysis of intuitionistic logic I: Formal systems and recursive functions (Crossely, J. N. and Dummett, M., editors), North-Holland, Amsterdam. (Semantical analysis of intuitionistic logic II, unpublished)Google Scholar
Lewis, H. [1979], Unsolvable classes of quantificational formulas, Addison Wesley, Reading, Massachusetts.Google Scholar
Maksimova, L. L. [1972], Pretabular superintuitionistic logics, Algebra i Logika, vol. 11, pp. 558–570.Google Scholar
Maslov, S. Yu., Mints, G. E., and Orevkov, V. P. [1965], Unsolvability in the constructive predicate calculus of certain classes of formulas containing only monadic predicate variables, Soviet Mathematics Doklady, vol. 6, pp. 918–920.Google Scholar
Mints, G. E. [1968], Some calculi of modal logic, Trudy Matematicheskogo Instituta imeni V. A. Steklova, vol. 98, pp. 88–111.Google Scholar
Mortimer, M. [1975], On languages with two variables, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 21, pp. 135–140.CrossRefGoogle Scholar
Ono, H. [1977], On some intuitionistic modal logics, Research Institute for Mathematical Sciences Publications, Kyoto University, vol. 13, pp. 687–722.Google Scholar
Scott, D. [1962], A decision method for validity of sentences in two variables, this Journal, vol. 27, p. 477.Google Scholar
Segerberg, K. [1973], Two-dimensional modal logic, Journal of Philosophical Logic, vol. 2, pp. 77–96.CrossRefGoogle Scholar
Shehtman, V. B. [1987], On some two-dimensional modal logics, 8th International Congress on Logic, Methodology and Philosophy of Science, Moscow, 1987, Nauka, Moscow, vol. 1, pp. 326–330. (Abstract)Google Scholar
Surańyi, J. [1943], Zur Reduktion des Entscheidungsproblems des logischen Funktionskalküls, Matematika Fizika Lepok, vol. 50, pp. 51–74.Google Scholar
Surańyi, J. [1959], Reduktionstheorie des Entscheidungsproblems in Prädikatenkalkül der ersten Stufe, Budapest.Google Scholar
Vardanyan, V. A. [1986], Arithmetic complexity of predicate logics of provability and their fragments, Soviet Mathematics Doklady, vol. 33, pp. 569–572.Google Scholar
Wajsberg, M. [1933], Ein erweiter Klassenkalkül, Monatschefte für Mathematische Physika, vol. 40, pp. 113–126.Google Scholar