Published online by Cambridge University Press: 12 March 2014
Einleitung. Das “Auswahlaxiom” oder “multiplicative axiom” fordert in der gewöhnlichen, von B. Russell und Zermelo angegebenen Fassung, daß zu jeder Menge M, deren Elemente paarweise fremde und nicht-leere Mengen sind, mindestens eine “Auswahlmenge” 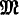 existiere, die mit jedem Element von M genau éin Element gemeinsam hat. Die nächstliegende und mehrfach verwendete Methode, um ein schwächeres Postulat als die vorstehende Fassung zu formulieren, besteht darin, daß man entweder über die Mächtigkeit der Menge M, oder über die Mächtigkeiten ihrer Elemente, oder über beides gleichzeitig, einschränkende Bedingungen macht, also nur in diesen eingeschränkten Fällen die Existenz einer Auswahlmenge verlangt. Hinsichtlich der Mächtigkeit von M ist da sogleich die Bemerkung zu machen, daß sie jedenfalls transfinit (genauer: nicht endlich im induktiven Sinn) anzusetzen ist. Vermöge allgemeiner logischer Sachverhalte und des (eventuell zu beweisenden) Prinzips, das zu einem gegebenen Objekt a die Bildung der Menge {a} erlaubt, ist nämlich die Existenz einer Auswahlmenge von M beweisbar, falls M die Mächtigkeit 1 besitzt, und diese Beweisbarkeit überträgt sich mittels gewöhnlicher Induktion auf den Fall einer beliebigen endlichen Mächtigkeit. Dagegen ist die Existenz einer Auswahlmenge nicht mehr beweisbar, wenn (bei transfinitem M) die Elemente von M endliche Mengen mit Mächtigkeiten > 1 sind, z. B. also schon in dem Fall, wo M eine transfinite Menge von Paaren ist—natürlich “im allgemeinen,” d. h. wenn die Elemente von M nicht eine besondere Beschaffenheit haben, die die Auszeichnung gewisser Elemente in ihnen ermöglicht. Die Tatsache dieser Nichtbeweisbarkeit, d. h. der Unabhängigkeit des Auswahlaxioms sogar in diesem einfachsten Fall, ist vor längerer Zeit auf der Basis des Zermeloschen Axiomensystems der Mengenlehre nachgewiesen worden.
existiere, die mit jedem Element von M genau éin Element gemeinsam hat. Die nächstliegende und mehrfach verwendete Methode, um ein schwächeres Postulat als die vorstehende Fassung zu formulieren, besteht darin, daß man entweder über die Mächtigkeit der Menge M, oder über die Mächtigkeiten ihrer Elemente, oder über beides gleichzeitig, einschränkende Bedingungen macht, also nur in diesen eingeschränkten Fällen die Existenz einer Auswahlmenge verlangt. Hinsichtlich der Mächtigkeit von M ist da sogleich die Bemerkung zu machen, daß sie jedenfalls transfinit (genauer: nicht endlich im induktiven Sinn) anzusetzen ist. Vermöge allgemeiner logischer Sachverhalte und des (eventuell zu beweisenden) Prinzips, das zu einem gegebenen Objekt a die Bildung der Menge {a} erlaubt, ist nämlich die Existenz einer Auswahlmenge von M beweisbar, falls M die Mächtigkeit 1 besitzt, und diese Beweisbarkeit überträgt sich mittels gewöhnlicher Induktion auf den Fall einer beliebigen endlichen Mächtigkeit. Dagegen ist die Existenz einer Auswahlmenge nicht mehr beweisbar, wenn (bei transfinitem M) die Elemente von M endliche Mengen mit Mächtigkeiten > 1 sind, z. B. also schon in dem Fall, wo M eine transfinite Menge von Paaren ist—natürlich “im allgemeinen,” d. h. wenn die Elemente von M nicht eine besondere Beschaffenheit haben, die die Auszeichnung gewisser Elemente in ihnen ermöglicht. Die Tatsache dieser Nichtbeweisbarkeit, d. h. der Unabhängigkeit des Auswahlaxioms sogar in diesem einfachsten Fall, ist vor längerer Zeit auf der Basis des Zermeloschen Axiomensystems der Mengenlehre nachgewiesen worden.
1 Von anderen Methoden der Abschwächung, die durchaus erfolgversprechend sein mögen, soll hier nicht die Rede sein. Erwähnt sei z. B. die Ersetzung des Auswahlprinzips durch das Ordnungsprinzip, d. h. durch das Postulat, daß es zu jeder Menge eine mit ihr im Elementebestand übereinstiminende geordnete Menge gibt. Auch das “principio di approssimazione” von Beppo Levi werde genannt; siehe etwa B. Levi in Fundamenta mathematicae, Bd. 23 (1934), S. 63–74, und T. Viola, ibid., S. 75–101, sowie die dort genannten älteren Arbeiten.
2 Hilbert, Siehe D. und Bernays, P., Grundlagen der Mathematik, Bd. 1 (Berlin 1934), S. 156–158 Google Scholar. Vgl. auch L'Enseignement mathématique, Bd. 34 (1935), S. 39–40 Google Scholar.
3 Fraenkel, A., Der Begriff “definit” und die Unabhängigkeit des Auswahlaxioms, Sitzungsberichte der Preußischen Akademie der Wissenschaften, phys.-math. Kl., 1922, S. 253–257 Google Scholar. Siehe dazu noch J. Merzbach, Inauguraldissertation, Marburg 1925, 4. Kapitel.
4 Zermelo, E., Untersuchungen über die Grundlagen der Mengenlehre I, Mathematische Annalen, Bd. 65 (1908), S. 261–281 CrossRefGoogle Scholar. Vgl. dazu Fraenkel, A., Mathematische Zeitschrift, Bd. 22 (1925), S. 250–273 CrossRefGoogle Scholar.
5 Zermelo, E., Über Grenzzahlen und Mengenbereiche, Fundamenta mathemcticae, Bd. 16 (1930), S. 29–47 CrossRefGoogle Scholar.
6 Fußnote, Siehe 4, ferner Journal für die reine und angewandte Mathematik, Bd. 155 (1926), S. 129–158 Google Scholar, und Bd. 167 (1932), S. 1–11.
7 Reelle Zahlen kann man natürlich stets als Mengen einer Mengenlehre auffassen, deren einziges Urelement die Nullmenge ist. Ob es mathematisch relevante Objekte gibt, die sich nicht so auffassen lassen, bleibe dahingestellt.
8 Ob und wie hier die Gleichheit auf ∈ zurückgefuhrt werden kann, ist für den Beweis gleichgültig und bleibe darum unerörtert. Man hätte hierbei zwischen Mengen und Urelementen zu unterscheiden.
9
“Es gibt” oder “es existiert” ein Objekt a soil heißen: das Objekt a kommt in ![]() vor. (Logischer Begriff; nicht zu vermischen mit der undefinierten Relation ∈.)
vor. (Logischer Begriff; nicht zu vermischen mit der undefinierten Relation ∈.)
10 Siehe die in Fußnoten 3, 4, 6 zitierten Arbeiten, sowie Aufsatz, Th. Skolems in Wissenschaftliche Vorträge gehalten auf dem 5. Kongreß der skandinavischen Mathematiker in Helsingfors 1922, Helsingfors 1923, S. 217–232 Google Scholar, und Zermelo, in Fundamenta mathematicae, Bd. 14 (1929), S. 339–344 CrossRefGoogle Scholar, nebst Skolems Bemerkungen hierzu, ibid., Bd. 15 (1930), S. 337–341.
11 Für die Beweisbarkeit der Existenz von 0 aus II1, 3, 4 vgl. die am Schluß von Fußnote 4 genannte Arbeit (Beginn des dortigen §2).
12 Siehe die in Fußnote 4 zitierte Arbeit Zermelos, S. 267 und 280.
13 Neumann, Vgl. J. v., Acta scient. math. (Szeged), Bd. 1 (1923), S. 199 Google Scholar.
14 Man kann die so bezeichneten Teilmengen von Z* etwas umständlicher auch ohne den Ordnungsbegriff charakterisieren.
15 Neumann, Vgl. J. v. im Journal für die reine und angewandte Mathematik, Bd. 154 (1925), S. 219–240 CrossRefGoogle Scholar (bes. 238–240) und meine Einleitung in die Mengenlehre, 3. Aufl. (Berlin 1928), S. 354–356 Google Scholar, sowie die dort angeführte Literatur.
16 Vgl. den genau analogen Beweis in Merzbachs Dissertation (siehe Fußnote 3), S. 34–35.
17 Natürlich könnte man auch diesen Prozeß nochmals induktiv aufspalten; doch dürfte obige Definition auch ohne solche Ausführlichkeit durchsichtig sein.
18 Entweder auf Grund der Bemerkung zu Ende des zweiten Absatzes dieses Beweises, oder auch wegen der Induktionsvoraussetzung vom Beginn dieses Absatzes.
19 Neumann, Siehe J. v. in Mathematische Annalen, Bd. 99 (1928), S. 373–391 CrossRefGoogle Scholar (speziell S. 377), und meinen Zusatz, ibid., S. 392 f. Vgl. auch den Beweis eines zu Hilfssatz 3 analogen Satzes in Kapitel 4 der (in Fußnote 3 zitierten) Merzbachschen Dissertation.
20 Diesen einfachen Beweis verdanke ich Max Schiffer (Jerusalem), wie auch die Erkenntnis der notwendigen Rücksicht auf die altemierende Gruppe in Hilfssatz 6 von Herrn Schiffer herrührt.
21
Dieser Einschluß der Relation ![]() soil sich im folgenden stets von selbst verstehen, auch ohne ausdrückliche Angabe. Die Relationen ϕ = ψ und ϕ ≠ ψ sind eo ipso eingeschlossen, da ϕ = ψ mit ϕ∈{ψ} gleichbedeutend ist.
soil sich im folgenden stets von selbst verstehen, auch ohne ausdrückliche Angabe. Die Relationen ϕ = ψ und ϕ ≠ ψ sind eo ipso eingeschlossen, da ϕ = ψ mit ϕ∈{ψ} gleichbedeutend ist.
22 Vgl. die Zitate der Fußnoten 6 und 19; ferner mein in Fußnote 15 genanntes Buch, S. 285–288.
23 Aus praktischen Gründen empfiehlt es sich, auch der Menge {a} dieselbe Klassenzahl beizulegen, die a besitzt. Doch ist das ohne prinzipielle Bedeutung. (Vgl. die Bemerkung zu Axiom II1 in §1.)
24 Dies ist die Stelle, um derentwillen im Beweis die Verwendung der “Halbsymmetrie” statt der schärferen Eigenschaft “Symmetrie” notwendig wird. Ginge man von der vollen Symmetric aus, so würde der Schluß hinsichtlich τ nicht zulässig sein; denn τ könnte z. B. ein Paar sein, dessen Symmetrie davon herrührt, daß seine beiden Elemente je halbsymmetrisch sind und durch eine ungerade Permutation in einander übergehen.
25 Hiermit soil nur eine einfache Bezeichnung der endlich vielen Elemente von τ eingeführt werden, nicht aber eine Auszeichnung einzelner Elemente (z. B. von t 1) durch Ordnung; denn ohne das (engste) Auswahlaxiom läßt sich eine Ordnung zwar im Einzelfall, nicht aber stets gleichzeitig hinsichtlich aller Elemente T von M durchführen.
26 Wegen der Verwendung aussondernder Funktionen zweier Argumente vgl. Definition 3 von §3. Für die obige und die im übernächsten Absatz folgende Verwendung (in Verbindung mit “irgend ein”) siehe speziell die zweite in Fußnote 4 genannte Arbeit, S. 259.