Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-22T20:32:32.094Z Has data issue: false hasContentIssue false
  • English
  • Français

Two arithmetical techniques with numbered classes

Published online by Cambridge University Press:  12 March 2014

Gerald B. Standley
Gerald B. Standley*
Affiliation:
University College, University of Florida
Get access Rights & Permissions [Opens in a new window]

Extract

If numbers be used to designate classes, there can be derived from a conjunct of classes numbers corresponding to the expanded product classes.

For example, let the product classes ābc and āb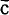 be designated by numbers I and 5 as in the following matrix:

By using 1 (20) instead of a, 2 (21) instead of b, 4 (22) instead of c, etc., the following relationship emerges between the designation of the conjunct of classes (take 12) and the product classes (I and 5): the product class(es) of any conjunct of classes is (are) (1) the sum of any negated class numbers and (2) seven less the sum of any unnegated class numbers.

Type
Reviews
Information
The Journal of Symbolic Logic , Volume 27 , Issue 4 , December 1962 , pp. 437 - 438
Copyright
Copyright © Association for Symbolic Logic 1962

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 Product class numbers will be italicized to avoid confusion with class numbers.

2 1, 2, and 6, as well as various other combinations, will also serve; but 1, 2, and 7 seems to be the simplest which still invalidates all (pseudo-) syllogisms repeating the middle term in the conclusion.