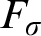Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T07:10:56.741Z Has data issue: false hasContentIssue false
  • English
  • Français

TUKEY ORDER AMONG $F_{\sigma }$ IDEALS

Part of: Set theory Ordered sets

Published online by Cambridge University Press:  06 May 2021

JIALIANG HE ,
MICHAEL HRUŠÁK ,
DIEGO ROJAS-REBOLLEDO  and
SŁAWOMIR SOLECKI
JIALIANG HE
Affiliation:
COLLEGE OF MATHEMATICSSICHUAN UNIVERSITYCHENGDU, SICHUAN610064, CHINAE-mail: [email protected]
MICHAEL HRUŠÁK
Affiliation:
CENTRO DE CIENCIAS MATEMÁTICAS UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICOMORELIA, MEXICOE-mail: [email protected]
DIEGO ROJAS-REBOLLEDO
Affiliation:
DEPARTMENT OF MATHEMATICS AND COMPUTING SCIENCES SAINT MARY’S UNIVERSITYHALIFAX, NS, CANADAE-mail: [email protected]
SŁAWOMIR SOLECKI
Affiliation:
DEPARTMENT OF MATHEMATICS CORNELL UNIVERSITYITHACA, NY14853, USAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the Tukey order in the class of 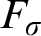$F_{\sigma }$ ideals of subsets of 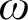$\omega $ . We show that no nontrivial 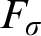$F_{\sigma }$ ideal is Tukey below a 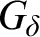$G_{\delta }$ ideal of compact sets. We introduce the notions of flat ideals and gradually flat ideals. We prove a dichotomy theorem for flat ideals isolating gradual flatness as the side of the dichotomy that is structurally good. We give diverse characterizations of gradual flatness among flat ideals using Tukey reductions and games. For example, we show that gradually flat ideals are precisely those flat ideals that are Tukey below the ideal of density zero sets.

Keywords

Tukey orderFσidealflat idealgradually flat ideal

MSC classification

Primary: 03E15: Descriptive set theory
Secondary: 03E05: Other combinatorial set theory 06A07: Combinatorics of partially ordered sets
Type
Article
Information
The Journal of Symbolic Logic , Volume 86 , Issue 2 , June 2021 , pp. 855 - 870
Check for updates
Copyright
© The Association for Symbolic Logic 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bartoszyński, T., Additivity of measure implies additivity of category . Transactions of the American Mathematical Society, vol. 281 (1984), pp. 209–213.10.2307/1999530CrossRefGoogle Scholar
Fremlin, D. H., The partially ordered sets of measure theory and Tukey’s ordering . Note di Matematica , vol. 11 (1991), pp. 177–214.Google Scholar
Fremlin, D. H., Games and the Tukey classification, notes, 2002. Available at https://www1.essex.ac.uk/maths/people/fremlin/preprints.htm.Google Scholar
Fremlin, D. H., Measure Theory , vol. 5, University of Essex, Colchester, 2008.Google Scholar
Hrušák, M., Combinatorics of filters and ideals , Set Theory and Its Applications (Babinkostova, L., Caicedo, A. E., Geschke, S., and Scheepers, M., editors), Contemporary Mathematics, vol. 533, American Mathematical Society, Providence, RI, 2011, pp. 29–69.10.1090/conm/533/10503CrossRefGoogle Scholar
Hrušák, M., Rojas-Rebolledo, D., and Zapletal, J., Cofinalities of Borel ideals . Mathematical Logic Quarterly, vol. 60 (2014), pp. 31–39.10.1002/malq.201200079CrossRefGoogle Scholar
Isbell, J. R., Seven cofinal types . Journal of the London Mathematical Society, vol. 4 (1972), pp. 651–654.10.1112/jlms/s2-4.4.651CrossRefGoogle Scholar
Kechris, A. S., Hereditary properties of the class of closed sets of uniqueness for trigonometric series . Israel Journal of Mathematics, vol. 73 (1991), pp. 189–198.10.1007/BF02772948CrossRefGoogle Scholar
Kechris, A. S., Louveau, A., and Woodin, W. H., The structure of $\sigma$ -ideals of compact sets . Transactions of the American Mathematical Society, vol. 301 (1987), pp. 263–288.Google Scholar
Louveau, A. and Veličković, B., Analytic ideals and cofinal types . The Annals of Pure and Applied Logic, vol. 99 (1999), pp. 171–195.10.1016/S0168-0072(98)00065-7CrossRefGoogle Scholar
Matheron, É. and Zelený, M., Descriptive set theory of families of small sets . The Bulletin of Symbolic Logic, vol. 13 (2007), pp. 482–537.10.2178/bsl/1203350880CrossRefGoogle Scholar
Mátrai, T., Kenilworth . Proceedings of the American Mathematical Society, vol. 137 (2009), pp. 1115–1125.10.1090/S0002-9939-08-09615-9CrossRefGoogle Scholar
Mátrai, T., Infinite dimensional perfect set theorems . Transactions of the American Mathematical Society, vol. 365 (2013), pp. 23–58.10.1090/S0002-9947-2012-05468-7CrossRefGoogle Scholar
Mazur, K., Fσ ideals and ${\omega}_1{\omega}_1^{\ast }$ -gaps in the Boolean algebras P(ω)/I . Fundamenta Mathematicae, vol. 138 (1991), pp. 103–111.10.4064/fm-138-2-103-111CrossRefGoogle Scholar
Moore, J. T. and Solecki, S., A ${G}_{\delta }$ ideal of compact sets strictly above the nowhere dense ideal in the Tukey order . The Annals of Pure and Applied Logic, vol. 156 (2008), pp. 270–273.10.1016/j.apal.2008.07.003CrossRefGoogle Scholar
Schmidt, J., Konfinalität . Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 1 (1955), pp. 271–303.10.1002/malq.19550010405CrossRefGoogle Scholar
Solecki, S., Gδ ideals of compact sets . Journal of the European Mathematical Society, vol. 13 (2011), pp. 853–882.10.4171/JEMS/268CrossRefGoogle Scholar
Solecki, S., Tukey reductions among analytic directed orders . Zbornik Radova (Beograd), vol. 17 (2015), no. 25, pp. 209–220 (Selected topics in combinatorial analysis).Google Scholar
Solecki, S. and Todorcevic, S., Cofinal types of topological directed orders . Annales de l'Institut Fourier, vol. 54 (2004), pp. 1877–1911.10.5802/aif.2070CrossRefGoogle Scholar
Solecki, S. and Todorcevic, S., Avoiding families and Tukey functions on the nowhere dense ideal . Journal of the Institute of Mathematics of Jussieu, vol. 10 (2011), pp. 405–435.10.1017/S1474748010000277CrossRefGoogle Scholar
Todorčević, S., Analytic gaps . Fundamenta Mathematicae, vol. 150 (1996), pp. 55–66.CrossRefGoogle Scholar
Tukey, J. W., Convergence and Uniformity in Topology , Annals of Mathematics Studies, vol. 2, Princeton University Press, Princeton, NJ, 1940.Google Scholar