Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-22T06:33:42.434Z Has data issue: false hasContentIssue false
  • English
  • Français

Trees

Published online by Cambridge University Press:  12 March 2014

Thomas J. Jech
Thomas J. Jech*
Affiliation:
Charles University Prague, Czechoslovakia
Get access Rights & Permissions [Opens in a new window]

Extract

This is an attempt to give a survey of recent results concerning trees. The article is an extended version of our talk in Oberwolfach (Schwarzwald) last May; the forests surrounding the Forschungsinstitut turned out to be a good inspiration.

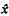A tree is a partially ordered set T = (T, ≤) such that for every x ∈ T, the set = {y ∈ T: y < x} is well-ordered. The order type of 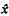is called the order of x, o(x), and the length of T is sup {o(x) + 1: x ∈ T}; an α-tree (where α is an ordinal) is a tree of length α. The αth level of T is the set Uα of all elements of T whose order is α. T∣α is the union of all Uβ, β < α; its length is α. A tree (T2, ≤2) is called an extension of (T1, ≤1) if ≤1 = ≤2 ∩ (T1 × T1); T2 is on end-extension of (T1 if T1 = T2∣α for some α. A maximal linearly ordered subset of a tree T is called a branch of T; an α-branch is a branch of length α.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 36 , Issue 1 , March 1971 , pp. 1 - 14
Copyright
Copyright © Association for Symbolic Logic 1971

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bukovsky, L., Consistency theorems connected with some combinatorial problems, Commentationes Mathematicae Universitatis Carolinae, vol. 7 (1966), pp. 495–499.Google Scholar
[2]Cohen, P. J., Set theory and the continuum hypothesis, W. A. Benjamin, Inc., New York, 1966.Google Scholar
[3]Hrbáček, K. M., A note on generalized Suslir's Problem, Commentationes Mathematicae Universitatis Carolinae, vol. 8 (1967), pp. 307–309.Google Scholar
[4]Jech, T. J., Non-provability of Suslir's hypothesis, Commentationes Mathematicae Universitatis Carolinae, vol. 8 (1967), pp. 291–305.Google Scholar
[5]Jensen, R. B., Notices of the American Mathematical Society, vol. 15 (1968), 935.Google Scholar
[6]Keisler, H. J. and Tarski, A., From accessible to inaccessible cardinals, Fundamenta Mathematicae, vol. 53 (1963–64), pp. 225–308.CrossRefGoogle Scholar
[7]Kurepa, D., L'hypothèse de ramification, Comptes Rendus Hebdomadaires des Séances de l' Academie des Sciences. Séries A et B, vol. 202 (1936), pp. 185–187.Google Scholar
[8]Marczewski, E. (Szpilrajn, E.), Séparabilité et multiplication cartésienne des espaces topologiques, Fundamenta Mathematicae, vol. 34 (1947), pp. 127–143.CrossRefGoogle Scholar
[9]Miller, E. W., A note on Suslin's Problem, American Journal of Mathematics, vol. 65 (1943), pp. 673–678.CrossRefGoogle Scholar
[10]Příkrý, K. L., Ph.D. Thesis, University of California, Berkeley, 1968.Google Scholar
[11]Rowbottom, F., Ph.D. Thesis, University of Wisconsin, Madison, 1965 (notes for 1967).Google Scholar
[12]Scott, D., Lectures on Boolean-valued models for set theory, Proceedings of the Summer Institute on Set Theory, U.C.L.A., 1967 (to appear).Google Scholar
[13]Sierpiński, W., Sur un problème de la théorie générale des ensembles équivalent au problème de Souslin, Fundamenta Mathematicae, vol. 35 (1948), pp. 165–174.CrossRefGoogle Scholar
[14]Silver, J., Ph.D. Thesis, University of California, Berkeley, 1966.Google Scholar
[15]Silver, J., The independence of Kurepa's conjecture and two-cardinal conjecture in model theory, Proceedings of the Summer Institute on Set Theory, U.C.L.A., 1967 (to appear).Google Scholar
[16]Solovay, R. M. and Tennenbaum, S., Iterated Cohen extensions and Suslir's Problem (to appear).Google Scholar
[17]Specker, E., Sur un problème de Sikorski, Colloquium Mathematicum, vol. 2 (1951), pp. 9–12.CrossRefGoogle Scholar
[18]Stewart, D. H., M.Sc. Thesis, Bristol, 1966.Google Scholar
[19]Souslin, M., Problème 3, Fundamenta Mathematicae, vol. 1 (1920), p. 223.Google Scholar
[20]Tennenbaum, S., Suslin's Problem, Proceedings of the National Academy of Sciences of the United States of America, vol. 59 (1968), pp. 60–63.CrossRefGoogle Scholar
[21]Vopénka, P. and Hájek, P., Sets, semisets, models, North-Holland (to appear).Google Scholar
[22]Kurepa, D., On A-trees, Publications de l'Institut Mathematique, vol. 8 (22), (1968), pp. 153–161.Google Scholar
[23]Gaifman, H. and Specker, E. P., Isomorphism types of trees, Proceedings of the American Mathematical Society, vol. 15 (1964), pp. 1–7.CrossRefGoogle Scholar
[24]Solovay, R., forthcoming paper on Kurepa trees.Google Scholar
[25]Jensen, R., SH is compatible with CH, (mimeographed).Google Scholar
[26]Jensen, R., SH = weak compactness in L, (mimeographed).Google Scholar