Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T02:26:46.703Z Has data issue: false hasContentIssue false
  • English
  • Français

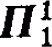Trees and -subsets of ω1ω1

Published online by Cambridge University Press:  12 March 2014

Alan Mekler  and
Jouko Väänänen
Alan Mekler
Affiliation:
Department of Mathematics, Simon Fraser University, Burnaby, Canada
Jouko Väänänen
Affiliation:
Department of Mathematics, University of Helsinki, Helsinki, Finland
Get access Rights & Permissions [Opens in a new window]

Abstract

We study descriptive set theory in the space by letting trees with no uncountable branches play a similar role as countable ordinals in traditional descriptive set theory. By using such trees, we get, for example, a covering property for the class of 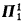-sets of .

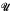We call a family of trees universal for a class of trees if 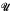⊆ and every tree in can be order-preservingly mapped into a tree in 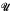. It is well known that the class of countable trees with no infinite branches has a universal family of size ℵ1. We shall study the smallest cardinality of a universal family for the class of trees of cardinality ≤ ℵ1 with no uncountable branches. We prove that this cardinality can be 1 (under ¬CH) and any regular cardinal κ which satisfies 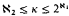(under CH). This bears immediately on the covering property of the 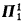-subsets of the space .

We also study the possible cardinalities of definable subsets of . We show that the statement that every definable subset of has cardinality <ωn or cardinality is equiconsistent with ZFC (if n ≥ 3) and with ZFC plus an inaccessible (if n = 2).

Finally, we define an analogue of the notion of a Borel set for the space and prove a Souslin-Kleene type theorem for this notion.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 58 , Issue 3 , September 1993 , pp. 1052 - 1070
Copyright
Copyright © Association for Symbolic Logic 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baumgartner, J., Harrington, L., and Kleinberg, E., Adding a closed unbounded set, this Journal, vol. 41 (1976), pp. 481–482.Google Scholar
[2]Blackwell, D., Borel sets via games, The Annals of Probability, vol. 9 (1981), pp. 321–322.CrossRefGoogle Scholar
[3]Halko, A., mimeographed notes, University of Helsinki, 1988.Google Scholar
[4]Hyttinen, T. and Tuuri, H., Constructing strongly equivalent nonisomorphic models for unstable theories, Annals of Pure and Applied Logic, vol. 52 (1991), pp. 203–248.CrossRefGoogle Scholar
[5]Hyttinen, T. and Väänänen, J., On Scott- and Karp-trees of uncountable models, this Journal, vol. 55 (1990), pp. 897–908.Google Scholar
[6]Jech, T., Set theory, Academic Press, San Diego, California, 1978.Google Scholar
[7]Juhász, I., Cardinal functions II, Handbook of set-theoretic topology (Kunen, K. and Vaughan, J. E., editors), North-Holland, Amsterdam, 1984, pp. 63–109.CrossRefGoogle Scholar
[8]Levy, A., Definability in axiomatic set theory II, Mathematical logic and foundations of set theory (Bar-Hillel, Y., editor), North-Holland, Amsterdam, 1970.Google Scholar
[9]Mekler, A. and Shelah, S., The Canary tree, Canadian Mathematical Bulletin (to appear).Google Scholar
[10]Nadel, M. and Stavi, J., L∞λ equivalence, isomorphism, and potential isomorphism, Transactions of American Mathematical Society, vol. 236 (1978), pp. 51–74.Google Scholar
[11]Shelah, S., Classification theory, revised edition, North-Holland, Amsterdam, 1990.Google Scholar
[12]Shelah, S., A weak generalization of MA to higher cardinals, Israel Journal of Mathematics, vol. 30 (1978), pp. 297–306.CrossRefGoogle Scholar
[13]Shelah, S., Tuuri, H., and Väänänen, J., On the number of automorphisms of uncountable models, this Journal (to appear).Google Scholar
[14]Solovay, R., A model of set-theory in which every set of reals is Lebesgue measurable, Annals of Mathematics, vol. 92 (1970), pp. 1–56.CrossRefGoogle Scholar
[15]Todorčević, S., Stationary sets, trees, and continuums, Publications de l’Institut Mathématique, Nouvelle Série, vol. 29 (43), Institut Mathématique, Belgrade, 1981, pp. 249–262.Google Scholar
[16]Tuuri, H., Relative separation theorems for Lκ+κ, Notre Dame Journal of Formal Logic, vol. 33 (1992), pp. 383–401.CrossRefGoogle Scholar
[17]Väänänen, J., A Cantor-Bendixson theorem for the space , Fundamenta Mathematicae, vol. 137 (1991), pp. 187–199.CrossRefGoogle Scholar
[18]Väänänen, J., Games and trees in infinitary logic: A survey, Quantifiers (Krynicki, M., Mostowski, M., and Szczerba, L., editors), Kluwer Academic Publishers, Dordrecht (to appear).Google Scholar