Published online by Cambridge University Press: 14 February 2022
We obtain an array of consistency results concerning trees and stationary reflection at double successors of regular cardinals
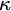 $\kappa $
, updating some classical constructions in the process. This includes models of
$\kappa $
, updating some classical constructions in the process. This includes models of
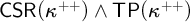 $\mathsf {CSR}(\kappa ^{++})\wedge {\sf TP}(\kappa ^{++})$
(both with and without
$\mathsf {CSR}(\kappa ^{++})\wedge {\sf TP}(\kappa ^{++})$
(both with and without
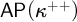 ${\sf AP}(\kappa ^{++})$
) and models of the conjunctions
${\sf AP}(\kappa ^{++})$
) and models of the conjunctions
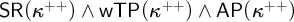 ${\sf SR}(\kappa ^{++}) \wedge \mathsf {wTP}(\kappa ^{++}) \wedge {\sf AP}(\kappa ^{++})$
and
${\sf SR}(\kappa ^{++}) \wedge \mathsf {wTP}(\kappa ^{++}) \wedge {\sf AP}(\kappa ^{++})$
and
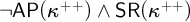 $\neg {\sf AP}(\kappa ^{++}) \wedge {\sf SR}(\kappa ^{++})$
(the latter was originally obtained in joint work by Krueger and the first author [9], and is here given using different methods). Analogs of these results with the failure of
$\neg {\sf AP}(\kappa ^{++}) \wedge {\sf SR}(\kappa ^{++})$
(the latter was originally obtained in joint work by Krueger and the first author [9], and is here given using different methods). Analogs of these results with the failure of
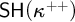 $\sf {SH}(\kappa ^{++})$
are given as well. Finally, we obtain all of our results with an arbitrarily large
$\sf {SH}(\kappa ^{++})$
are given as well. Finally, we obtain all of our results with an arbitrarily large
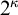 $2^\kappa $
, applying recent joint work by Honzik and the third author.
$2^\kappa $
, applying recent joint work by Honzik and the third author.