Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T06:20:57.275Z Has data issue: false hasContentIssue false
  • English
  • Français

THE TREE PROPERTY AT THE TWO IMMEDIATE SUCCESSORS OF A SINGULAR CARDINAL

Part of: Set theory

Published online by Cambridge University Press:  10 July 2020

JAMES CUMMINGS ,
YAIR HAYUT ,
MENACHEM MAGIDOR ,
ITAY NEEMAN ,
DIMA SINAPOVA  and
SPENCER UNGER
JAMES CUMMINGS
Affiliation:
DEPARTMENT OF MATHEMATICAL SCIENCES CARNEGIE MELLON UNIVERSITYPITTSBURGH, PA15213-3890, USAE-mail:[email protected]
YAIR HAYUT
Affiliation:
EINSTEIN INSTITUTE OF MATHEMATICS THE HEBREW UNIVERSITY OF JERUSALEMJERUSALEM9190401, ISRAELE-mail:[email protected]@savion.huji.ac.il
MENACHEM MAGIDOR
Affiliation:
EINSTEIN INSTITUTE OF MATHEMATICS THE HEBREW UNIVERSITY OF JERUSALEMJERUSALEM9190401, ISRAELE-mail:[email protected]@savion.huji.ac.il
ITAY NEEMAN
Affiliation:
MATHEMATICS DEPARTMENT UCLALOS ANGELES, CA90095-1555, USAE-mail:[email protected]
DIMA SINAPOVA
Affiliation:
DEPARTMENT OF MATHEMATICS, STATISTICS, AND COMPUTER SCIENCE UNIVERSITY OF ILLINOIS AT CHICAGOCHICAGO, IL60613, USAE-mail:[email protected]
SPENCER UNGER
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF TORONTOTORONTO, ON, M5S 2E4, CANADAE-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present an alternative proof that from large cardinals, we can force the tree property at 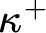$\kappa ^+$ and 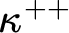$\kappa ^{++}$ simultaneously for a singular strong limit cardinal 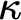$\kappa $ . The advantage of our method is that the proof of the tree property at the double successor is simpler than in the existing literature. This new approach also works to establish the result for 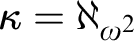$\kappa =\aleph _{\omega ^2}$ .

Keywords

tree propertysingular cardinalforcing

MSC classification

Primary: 03E35: Consistency and independence results
Secondary: 03E55: Large cardinals
Type
Article
Information
The Journal of Symbolic Logic , Volume 86 , Issue 2 , June 2021 , pp. 600 - 608
Check for updates
Copyright
© The Association for Symbolic Logic 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cummings, J. and Foreman, M., The tree property. Advances in Mathematics, vol. 133 (1998), no. 1, pp. 1–32.CrossRefGoogle Scholar
Gitik, M. and Sharon, A., On SCH and the approachability property. Proceedings of the American Mathematical Society, vol. 136 (2008), no. 1, pp. 311–320.CrossRefGoogle Scholar
Mitchell, W., Aronszajn trees and the independence of the transfer property. Annals of Mathematical Logic, vol. 5 (1972/73), pp. 21–46.CrossRefGoogle Scholar
Neeman, I., Aronszajn trees and failure of the singular cardinal hypothesis. Journal of Mathematical Logic, vol. 9 (2009), no. 1, pp. 139–157.CrossRefGoogle Scholar
Sinapova, D., The tree property at the first and double successors of a singular. Israel Journal of Mathematics, vol. 216 (2016), no. 2, pp. 799–810.CrossRefGoogle Scholar
Sinapova, D. and Unger, S., The tree property at ${\aleph}_{\omega^2+1}$  and  ${\aleph}_{\omega^2+2}$ , this Journal, vol. 83 (2018), no. 2, pp. 669–682.Google Scholar
Unger, S., Aronszajn trees and the successors of a singular cardinal. Archive for Mathematical Logic, vol. 52 (2013), no. 5–6, pp. 483–496.CrossRefGoogle Scholar