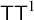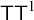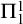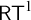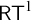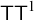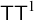1 Introduction
The classical pigeonehole principle, that an infinite set partitioned into finitely many parts must contain at least one part that is infinite, is elementary yet deeply fascinating in terms of its logical content. In computability theory and proof theory in particular, where the focus is on partitions of the set of natural numbers, it has been a subject of considerable interest. Formally, the statement is as follows, where we use
![]() $\omega $
to denote
$\omega $
to denote
![]() $\{ 0,1,2,\ldots \}$
.
$\{ 0,1,2,\ldots \}$
.
Statement 1.1 (Infinitary pigeonhole principle).
For every
![]() $k \geq 1$
and every
$k \geq 1$
and every
![]() $f : \omega \to k$
, there exists
$f : \omega \to k$
, there exists
![]() $i < k$
such that
$i < k$
such that
![]() $f^{-1}(\{ i \})$
is infinite.
$f^{-1}(\{ i \})$
is infinite.
In the study of models of arithmetic and reverse mathematics, the principle is non-trivial because of the possibility that the set of natural numbers, and the number k above, may be non-standard. In computable analysis, on the other hand, it is non-trivial because of the fact that the number
![]() $i < k$
cannot, in general, be found by any uniform algorithm. These features have inspired extensive investigations into the computational and proof-theoretic aspects of the infinitary pigeonhole principle, and in its relationship to various other logical and mathematical statements. Standard references on reverse mathematics include Simpson [Reference Simpson24], Hirschfeldt [Reference Hirschfeldt16], and Dzhafarov and Mummert [Reference Dzhafarov and Mummert12]. In Section 2, we review some rudiments of computable analysis in the style of Weihrauch [Reference Weihrauch28, Reference Weihrauch29], which will be our focus here. We refer to [Reference Dzhafarov and Mummert12, Chapter 4] for more details and examples, and to Brattka, Gherardi, and Pauly [Reference Brattka, Gherardi and Pauly1] for a comprehensive overview of the subject. For a general introduction to computability theory, see Soare [Reference Soare25] and Downey and Hirschfeldt [Reference Dzhafarov and Hirst11].
$i < k$
cannot, in general, be found by any uniform algorithm. These features have inspired extensive investigations into the computational and proof-theoretic aspects of the infinitary pigeonhole principle, and in its relationship to various other logical and mathematical statements. Standard references on reverse mathematics include Simpson [Reference Simpson24], Hirschfeldt [Reference Hirschfeldt16], and Dzhafarov and Mummert [Reference Dzhafarov and Mummert12]. In Section 2, we review some rudiments of computable analysis in the style of Weihrauch [Reference Weihrauch28, Reference Weihrauch29], which will be our focus here. We refer to [Reference Dzhafarov and Mummert12, Chapter 4] for more details and examples, and to Brattka, Gherardi, and Pauly [Reference Brattka, Gherardi and Pauly1] for a comprehensive overview of the subject. For a general introduction to computability theory, see Soare [Reference Soare25] and Downey and Hirschfeldt [Reference Dzhafarov and Hirst11].
A further point of interest is that the infinitary pigeonhole principle may be formulated as a special case of Ramsey’s theorem.
Statement 1.2 (Ramsey’s theorem for singletons).
For every
![]() $k \geq 1$
and every
$k \geq 1$
and every
![]() $f : \omega \to k$
, there exists an infinite set
$f : \omega \to k$
, there exists an infinite set
![]() $M \subseteq \omega $
monochromatic for f (i.e., such that
$M \subseteq \omega $
monochromatic for f (i.e., such that
![]() $f \operatorname {\mathrm {\upharpoonright }} M$
is constant).
$f \operatorname {\mathrm {\upharpoonright }} M$
is constant).
We denote this statement by
![]() $\mathsf {RT}^1$
. The equivalence of the two statements is obvious: given
$\mathsf {RT}^1$
. The equivalence of the two statements is obvious: given
![]() $i < k$
such that
$i < k$
such that
![]() $f^{-1}(\{ i \})$
is infinite we have that
$f^{-1}(\{ i \})$
is infinite we have that
![]() $M = \{ x \in \omega : f(x) = i \}$
is an infinite monochromatic set for f, and given M we have that
$M = \{ x \in \omega : f(x) = i \}$
is an infinite monochromatic set for f, and given M we have that
![]() $f^{-1}(\{ \min M \})$
is infinite. Importantly, this equivalence is uniform in the sense of Weihrauch reducibility (see, e.g., [Reference Dzhafarov and Mummert12, Proposition 4.3.4]).
$f^{-1}(\{ \min M \})$
is infinite. Importantly, this equivalence is uniform in the sense of Weihrauch reducibility (see, e.g., [Reference Dzhafarov and Mummert12, Proposition 4.3.4]).
In this paper, we are interested in a version of the pigeonhole principle not for partitions of
![]() $\omega $
but for partitions of trees. To state it, we begin with some definitions. We let
$\omega $
but for partitions of trees. To state it, we begin with some definitions. We let
![]() $\omega ^{<\omega }$
denote the set of all finite strings of natural numbers (i.e., functions
$\omega ^{<\omega }$
denote the set of all finite strings of natural numbers (i.e., functions
![]() $n \to \omega $
for some
$n \to \omega $
for some
![]() $n \in \omega $
), and
$n \in \omega $
), and
![]() $2^{<\omega }$
the subset of
$2^{<\omega }$
the subset of
![]() $\omega ^{<\omega }$
of all finite strings of
$\omega ^{<\omega }$
of all finite strings of
![]() $0$
s and
$0$
s and
![]() $1$
s (i.e., functions
$1$
s (i.e., functions
![]() $n \to 2$
for some
$n \to 2$
for some
![]() $n \in \omega $
). We will typically use lowercase Greek letters near the beginning of the alphabet (
$n \in \omega $
). We will typically use lowercase Greek letters near the beginning of the alphabet (
![]() $\alpha ,\beta ,\gamma ,\ldots $
) for general elements of
$\alpha ,\beta ,\gamma ,\ldots $
) for general elements of
![]() $\omega ^{<\omega }$
, and lowercase Greek letters near the middle of the alphabet (
$\omega ^{<\omega }$
, and lowercase Greek letters near the middle of the alphabet (
![]() $\sigma ,\tau ,\rho ,\ldots $
) for elements specifically of
$\sigma ,\tau ,\rho ,\ldots $
) for elements specifically of
![]() $2^{<\omega }$
. For
$2^{<\omega }$
. For
![]() $n \in \omega $
, we let
$n \in \omega $
, we let
![]() $\omega ^{< n}$
and
$\omega ^{< n}$
and
![]() $2^{< n}$
denote the respective restrictions of
$2^{< n}$
denote the respective restrictions of
![]() $\omega ^{<\omega }$
and
$\omega ^{<\omega }$
and
![]() $2^{<\omega }$
to strings of length less than n. We denote the length of a string
$2^{<\omega }$
to strings of length less than n. We denote the length of a string
![]() $\alpha \in \omega ^{<\omega }$
by
$\alpha \in \omega ^{<\omega }$
by
![]() $|\alpha |$
, and let
$|\alpha |$
, and let
![]() $\langle \rangle $
denote the empty string (i.e., the unique string of length
$\langle \rangle $
denote the empty string (i.e., the unique string of length
![]() $0$
). We use
$0$
). We use
![]() $\preceq $
for the reflexive prefix relation on
$\preceq $
for the reflexive prefix relation on
![]() $\omega ^{<\omega }$
, and
$\omega ^{<\omega }$
, and
![]() $\prec $
for the irreflexive. For
$\prec $
for the irreflexive. For
![]() $\alpha ,\beta \in \omega ^{<\omega }$
we write
$\alpha ,\beta \in \omega ^{<\omega }$
we write
![]() $\alpha \mid \beta $
if
$\alpha \mid \beta $
if
![]() $\alpha \npreceq \beta $
and
$\alpha \npreceq \beta $
and
![]() $\beta \npreceq \alpha $
. If
$\beta \npreceq \alpha $
. If
![]() $\alpha \mid \beta $
then
$\alpha \mid \beta $
then
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are called incomparable, and otherwise they are called comparable. We write
$\beta $
are called incomparable, and otherwise they are called comparable. We write
![]() $\alpha \beta $
for the concatenation of
$\alpha \beta $
for the concatenation of
![]() $\alpha $
by
$\alpha $
by
![]() $\beta $
(i.e., the string
$\beta $
(i.e., the string
![]() $\gamma $
of length
$\gamma $
of length
![]() $|\alpha |+|\beta |$
with
$|\alpha |+|\beta |$
with
![]() $\gamma (x) = \alpha (x)$
for all
$\gamma (x) = \alpha (x)$
for all
![]() $x < |\alpha |$
and
$x < |\alpha |$
and
![]() $\gamma (x) = \beta (x-|\alpha |)$
for
$\gamma (x) = \beta (x-|\alpha |)$
for
![]() $|\alpha | \leq x < |\alpha |+|\beta |$
). For
$|\alpha | \leq x < |\alpha |+|\beta |$
). For
![]() $s \in \omega $
, we write
$s \in \omega $
, we write
![]() $0^s$
for the string
$0^s$
for the string
![]() $\alpha $
of length s with
$\alpha $
of length s with
![]() $\alpha (x) = 0$
for all
$\alpha (x) = 0$
for all
![]() $x < s$
, and similarly for
$x < s$
, and similarly for
![]() $1^s$
.
$1^s$
.
Definition 1.3. Fix
![]() $S \subseteq 2^{<\omega }$
.
$S \subseteq 2^{<\omega }$
.
-
(1) For
 $n \in \omega \cup \{ \omega \}$
, we write
$n \in \omega \cup \{ \omega \}$
, we write
 $S \cong 2^{< n}$
if
$S \cong 2^{< n}$
if
 $(S,\preceq )$
and
$(S,\preceq )$
and
 $(2^{< n},\preceq )$
are isomorphic as partial orders.
$(2^{< n},\preceq )$
are isomorphic as partial orders. -
(2) For
 $k \geq 1$
, a k-coloring of S is a map
$k \geq 1$
, a k-coloring of S is a map
 $f : S \to k = \{ 0,\ldots ,k-1 \}$
.
$f : S \to k = \{ 0,\ldots ,k-1 \}$
. -
(3) A coloring of S is a k-coloring of S for some
 $k \geq 1$
.
$k \geq 1$
. -
(4) A set
 $H \subseteq S$
is monochromatic for a coloring f of S if f is constant on H. We call
$H \subseteq S$
is monochromatic for a coloring f of S if f is constant on H. We call
 $f(\min H)$
the color of H under f.
$f(\min H)$
the color of H under f.
The focus of our investigation is the following principle, originally formulated by Chubb, Hirst, and McNicholl [Reference Chubb, Hirst and McNicholl5].
Statement 1.4 (Tree pigeonhole principle).
For every
![]() $k \geq 1$
and every
$k \geq 1$
and every
![]() $f : 2^{<\omega } \to k$
, there exists
$f : 2^{<\omega } \to k$
, there exists
![]() $H \cong 2^{<\omega }$
that is monochromatic for f.
$H \cong 2^{<\omega }$
that is monochromatic for f.
We denote this statement by
![]() $\mathsf {TT}^1$
. Its proof is straightforward, though less trivial than that of
$\mathsf {TT}^1$
. Its proof is straightforward, though less trivial than that of
![]() $\mathsf {RT}^1$
. Consider a coloring
$\mathsf {RT}^1$
. Consider a coloring
![]() $f : 2^{<\omega } \to 2$
, for simplicity. If
$f : 2^{<\omega } \to 2$
, for simplicity. If
![]() $\{ \tau \in 2^{<\omega } : f(\tau ) = 0 \}$
is dense (meaning that for every
$\{ \tau \in 2^{<\omega } : f(\tau ) = 0 \}$
is dense (meaning that for every
![]() $\sigma \in 2^{<\omega }$
there exists
$\sigma \in 2^{<\omega }$
there exists
![]() $\tau \succeq \sigma $
with
$\tau \succeq \sigma $
with
![]() $f(\tau ) = 0$
) then an
$f(\tau ) = 0$
) then an
![]() $H \cong 2^{<\omega }$
monochromatic for f with color
$H \cong 2^{<\omega }$
monochromatic for f with color
![]() $0$
can be easily constructed by unbounded search. Otherwise, there exists
$0$
can be easily constructed by unbounded search. Otherwise, there exists
![]() $\sigma \in 2^{<\omega }$
such that
$\sigma \in 2^{<\omega }$
such that
![]() $f(\tau ) = 1$
for all
$f(\tau ) = 1$
for all
![]() $\tau \succeq \sigma $
, and then
$\tau \succeq \sigma $
, and then
![]() $H = \{ \tau \in 2^{<\omega } : \tau \succeq \sigma \} \cong 2^{<\omega }$
is monochromatic for f with color
$H = \{ \tau \in 2^{<\omega } : \tau \succeq \sigma \} \cong 2^{<\omega }$
is monochromatic for f with color
![]() $1$
. Such an H is sometimes called a monochromatic cone, leading to this proof being called a “dense-or-cone” argument. More generally, given
$1$
. Such an H is sometimes called a monochromatic cone, leading to this proof being called a “dense-or-cone” argument. More generally, given
![]() $f : 2^{<\omega } \to k$
, an iteration of this argument reveals an
$f : 2^{<\omega } \to k$
, an iteration of this argument reveals an
![]() $i < k$
and a
$i < k$
and a
![]() $\sigma \in 2^{<\omega }$
such that
$\sigma \in 2^{<\omega }$
such that
![]() $\{ \tau \in 2^{<\omega } : f(\tau ) = i \}$
is dense above
$\{ \tau \in 2^{<\omega } : f(\tau ) = i \}$
is dense above
![]() $\sigma $
, from which an
$\sigma $
, from which an
![]() $H \cong 2^{<\omega }$
monochromatic for f with color i may be constructed. We will explore variations on “dense-or-cone” arguments in Section 3.
$H \cong 2^{<\omega }$
monochromatic for f with color i may be constructed. We will explore variations on “dense-or-cone” arguments in Section 3.
In the literature,
![]() $\mathsf {TT}^1$
and its generalizations to higher dimensions have collectively come to be called the tree theorem. However, it is worth emphasizing that the sets
$\mathsf {TT}^1$
and its generalizations to higher dimensions have collectively come to be called the tree theorem. However, it is worth emphasizing that the sets
![]() $H \cong 2^{<\omega }$
it deals with are not trees in the usual sense used in computability theory. More precisely, a set
$H \cong 2^{<\omega }$
it deals with are not trees in the usual sense used in computability theory. More precisely, a set
![]() $H \cong 2^{<\omega }$
need not be closed downward under
$H \cong 2^{<\omega }$
need not be closed downward under
![]() $\preceq $
. The notion also differs from the usual sense of trees used in descriptive set theory, in that such an H need not preserve meets (i.e., least common prefixes). A partition principle better suited to the latter type of structure is the Halpern-Läuchli theorem (or Milliken’s tree theorem, as it is known in higher dimensions) which generalizes the Chubb–Hirst–McNicholl version we will focus on here. (See Todorčević [Reference Todorcevic27] and Dobrinen [Reference Dobrinen8] for more details, and Anglés d’Auriac, et al. [Reference Anglès d’Auriac, Cholak, Dzhafarov, Monin and Patey7] for a recent computability-theoretic analysis.) We will use the word “tree” exclusively in the computability-theoretic sense throughout this paper, and refer to Statement 1.4 and its variants (introduced below) only by
$\preceq $
. The notion also differs from the usual sense of trees used in descriptive set theory, in that such an H need not preserve meets (i.e., least common prefixes). A partition principle better suited to the latter type of structure is the Halpern-Läuchli theorem (or Milliken’s tree theorem, as it is known in higher dimensions) which generalizes the Chubb–Hirst–McNicholl version we will focus on here. (See Todorčević [Reference Todorcevic27] and Dobrinen [Reference Dobrinen8] for more details, and Anglés d’Auriac, et al. [Reference Anglès d’Auriac, Cholak, Dzhafarov, Monin and Patey7] for a recent computability-theoretic analysis.) We will use the word “tree” exclusively in the computability-theoretic sense throughout this paper, and refer to Statement 1.4 and its variants (introduced below) only by
![]() $\mathsf {TT}^1$
and similar initialisms.
$\mathsf {TT}^1$
and similar initialisms.
It is well-known that
![]() $\mathsf {RT}^1$
is a consequence of
$\mathsf {RT}^1$
is a consequence of
![]() $\mathsf {TT}^1$
. The following argument, which we include for completeness, was first noted in [Reference Chubb, Hirst and McNicholl5, proof of Theorem 1.5]. Given
$\mathsf {TT}^1$
. The following argument, which we include for completeness, was first noted in [Reference Chubb, Hirst and McNicholl5, proof of Theorem 1.5]. Given
![]() $g : \omega \to k$
, define
$g : \omega \to k$
, define
![]() $f : 2^{<\omega } \to k$
by
$f : 2^{<\omega } \to k$
by
![]() $f(\sigma ) = g(|\sigma |)$
. By the tree pigeonhole principle, we may fix an
$f(\sigma ) = g(|\sigma |)$
. By the tree pigeonhole principle, we may fix an
![]() $H \cong 2^{<\omega }$
monochromatic for f, say with color
$H \cong 2^{<\omega }$
monochromatic for f, say with color
![]() $i < k$
. Then
$i < k$
. Then
![]() $\{ |\sigma | : \sigma \in H \}$
is an infinite monochromatic set for g, so in particular,
$\{ |\sigma | : \sigma \in H \}$
is an infinite monochromatic set for g, so in particular,
![]() $g^{-1}(\{ i \})$
is infinite.
$g^{-1}(\{ i \})$
is infinite.
Finding the precise relationship between
![]() $\mathsf {RT}^1$
and
$\mathsf {RT}^1$
and
![]() $\mathsf {TT}^1$
is an ongoing investigation using the framework of reverse mathematics. Here,
$\mathsf {TT}^1$
is an ongoing investigation using the framework of reverse mathematics. Here,
![]() $\mathsf {RT}^1$
and
$\mathsf {RT}^1$
and
![]() $\mathsf {TT}^1$
are formalized in the language of second-order arithmetic, and their strengths are calibrated in terms of implications over the weak base theory
$\mathsf {TT}^1$
are formalized in the language of second-order arithmetic, and their strengths are calibrated in terms of implications over the weak base theory
![]() $\mathsf {RCA}_0$
(or sometimes, even weaker systems). By a well-known result of Hirst [Reference Hirst18, Theorem 6.4],
$\mathsf {RCA}_0$
(or sometimes, even weaker systems). By a well-known result of Hirst [Reference Hirst18, Theorem 6.4],
![]() $\mathsf {RT}^1$
is equivalent over
$\mathsf {RT}^1$
is equivalent over
![]() $\mathsf {RCA}_0$
to the bounding scheme
$\mathsf {RCA}_0$
to the bounding scheme
![]() $\mathsf {B}\Sigma ^0_2$
(which, by classic results, itself lies strictly in-between the induction schemes
$\mathsf {B}\Sigma ^0_2$
(which, by classic results, itself lies strictly in-between the induction schemes
![]() $\mathsf {I}\Sigma ^0_1$
and
$\mathsf {I}\Sigma ^0_1$
and
![]() $\mathsf {I}\Sigma ^0_2$
). Corduan, Groszek, and Mileti [Reference Corduan, Groszek and Mileti6, Section 3.3] obtained the surprising result that
$\mathsf {I}\Sigma ^0_2$
). Corduan, Groszek, and Mileti [Reference Corduan, Groszek and Mileti6, Section 3.3] obtained the surprising result that
![]() $\mathsf {TT}^1$
lies strictly above
$\mathsf {TT}^1$
lies strictly above
![]() $\mathsf {B}\Sigma ^0_2$
, while Chong, Li, Wei, and Yang [Reference Chong, Li, Wang and Yang4, Corollary 4.2] proved it is strictly below
$\mathsf {B}\Sigma ^0_2$
, while Chong, Li, Wei, and Yang [Reference Chong, Li, Wang and Yang4, Corollary 4.2] proved it is strictly below
![]() $\mathsf {I}\Sigma ^0_2$
. Thus, we know that
$\mathsf {I}\Sigma ^0_2$
. Thus, we know that
![]() $\mathsf {TT}^1$
is a stronger principle than
$\mathsf {TT}^1$
is a stronger principle than
![]() $\mathsf {RT}^1$
, but more questions remain. Chief among these is whether
$\mathsf {RT}^1$
, but more questions remain. Chief among these is whether
![]() $\mathsf {TT}^1$
is conservative for
$\mathsf {TT}^1$
is conservative for
![]() $\Pi ^1_1$
sentences over
$\Pi ^1_1$
sentences over
![]() $\mathsf {RCA}_0 + \mathsf {RT}^1$
. In particular, it is possible that the first-order part of
$\mathsf {RCA}_0 + \mathsf {RT}^1$
. In particular, it is possible that the first-order part of
![]() $\mathsf {TT}^1$
(i.e., the set of its first-order consequences over
$\mathsf {TT}^1$
(i.e., the set of its first-order consequences over
![]() $\mathsf {RCA}_0$
) is exactly (the set of such consequences of)
$\mathsf {RCA}_0$
) is exactly (the set of such consequences of)
![]() $\mathsf {RT}^1$
.
$\mathsf {RT}^1$
.
In this article, we investigate the strength of
![]() $\mathsf {TT}^1$
, and its relationship to
$\mathsf {TT}^1$
, and its relationship to
![]() $\mathsf {RT}^1$
, using the tools of Weihrauch reducibility and Weihrauch-style computable analysis. This is a different framework from reverse mathematics, but one that is often complementary (see Dorais, et al., [Reference Dorais, Dzhafarov, Hirst, Mileti and Shafer9, Section 1] for a discussion). In many cases, the results in this approach provide a finer, more detailed view of those in classical reverse mathematics. We obtain a number of results along these lines below. Recently, Dzhafarov, Solomon, and Yokoyama [Reference Dzhafarov, Solomon and Yokoyama13] introduced an analog for Weihrauch reducibility of the first-order part of a problem (defined precisely in the next section). We show that, for the most natural way of formulating
$\mathsf {RT}^1$
, using the tools of Weihrauch reducibility and Weihrauch-style computable analysis. This is a different framework from reverse mathematics, but one that is often complementary (see Dorais, et al., [Reference Dorais, Dzhafarov, Hirst, Mileti and Shafer9, Section 1] for a discussion). In many cases, the results in this approach provide a finer, more detailed view of those in classical reverse mathematics. We obtain a number of results along these lines below. Recently, Dzhafarov, Solomon, and Yokoyama [Reference Dzhafarov, Solomon and Yokoyama13] introduced an analog for Weihrauch reducibility of the first-order part of a problem (defined precisely in the next section). We show that, for the most natural way of formulating
![]() $\mathsf {TT}^1$
and
$\mathsf {TT}^1$
and
![]() $\mathsf {RT}^1$
in the context of Weihrauch reducibility, the first-order part of
$\mathsf {RT}^1$
in the context of Weihrauch reducibility, the first-order part of
![]() $\mathsf {TT}^1$
in the sense of [Reference Dzhafarov, Solomon and Yokoyama13] is precisely
$\mathsf {TT}^1$
in the sense of [Reference Dzhafarov, Solomon and Yokoyama13] is precisely
![]() $\mathsf {RT}^1$
. Thus, we obtain a positive answer to the analog of the question above. As shown in [Reference Dzhafarov, Solomon and Yokoyama13], and in follow-up works by Soldà and Valenti [Reference Soldà and Valenti26] and Goh, Pauly, and Valenti [Reference Le Goh, Pauly and Valenti15], this new notion of “first-order part” largely agrees with the one from reverse mathematics. Thus, our results may be viewed as evidence in support of the corresponding answers for the original question, too.
$\mathsf {RT}^1$
. Thus, we obtain a positive answer to the analog of the question above. As shown in [Reference Dzhafarov, Solomon and Yokoyama13], and in follow-up works by Soldà and Valenti [Reference Soldà and Valenti26] and Goh, Pauly, and Valenti [Reference Le Goh, Pauly and Valenti15], this new notion of “first-order part” largely agrees with the one from reverse mathematics. Thus, our results may be viewed as evidence in support of the corresponding answers for the original question, too.
Before moving on, we include one final remark for general interest. By its equivalence with the infinitary pigeonhole principle,
![]() $\mathsf {RT}^1$
may be regarded as either a second-order statement (asserting the existence of certain kinds of sets) or as a first-order (arithmetical) statement. Interestingly, the same is not true of
$\mathsf {RT}^1$
may be regarded as either a second-order statement (asserting the existence of certain kinds of sets) or as a first-order (arithmetical) statement. Interestingly, the same is not true of
![]() $\mathsf {TT}^1$
, as we learned from Leszek Kołodziejczyk (private communication). We include the argument he supplied as it is quite lovely but appears to be missing from the literature. As discussed above, Chong, Li, Wei, and Yang [Reference Chong, Li, Wang and Yang4, Corollary 4.2] exhibited a model
$\mathsf {TT}^1$
, as we learned from Leszek Kołodziejczyk (private communication). We include the argument he supplied as it is quite lovely but appears to be missing from the literature. As discussed above, Chong, Li, Wei, and Yang [Reference Chong, Li, Wang and Yang4, Corollary 4.2] exhibited a model
![]() $(M,\mathcal {S})$
of
$(M,\mathcal {S})$
of
![]() $\mathsf {RCA}_0 + \neg \mathsf {I}\Sigma ^0_2 + \mathsf {TT}^1$
. By results of Corduan, Groszek, and Mileti [Reference Corduan, Groszek and Mileti6, Proposition 3.5], there is an
$\mathsf {RCA}_0 + \neg \mathsf {I}\Sigma ^0_2 + \mathsf {TT}^1$
. By results of Corduan, Groszek, and Mileti [Reference Corduan, Groszek and Mileti6, Proposition 3.5], there is an
![]() $X \in \mathcal {S}$
such that some
$X \in \mathcal {S}$
such that some
![]() $\mathsf {TT}^1$
instance f computable from X (in the sense of M) has no solution computable from X. Consider the topped model
$\mathsf {TT}^1$
instance f computable from X (in the sense of M) has no solution computable from X. Consider the topped model
![]() $M[X]$
, which has first-order part M and second order part the set of all
$M[X]$
, which has first-order part M and second order part the set of all
![]() $Y \subseteq M$
computable from X. Then
$Y \subseteq M$
computable from X. Then
![]() $\mathsf {RCA}_0$
holds in
$\mathsf {RCA}_0$
holds in
![]() $M[X]$
but
$M[X]$
but
![]() $\mathsf {TT}^1$
fails, as witnessed by f. But
$\mathsf {TT}^1$
fails, as witnessed by f. But
![]() $(M,\mathcal {S})$
and
$(M,\mathcal {S})$
and
![]() $M[X]$
have the same first-order part (namely, M) and thus satisfy the same
$M[X]$
have the same first-order part (namely, M) and thus satisfy the same
![]() $\Pi ^1_1$
sentences. Any
$\Pi ^1_1$
sentences. Any
![]() $\Pi ^1_1$
statement equivalent over
$\Pi ^1_1$
statement equivalent over
![]() $\mathsf {RCA}_0$
to
$\mathsf {RCA}_0$
to
![]() $\mathsf {TT}^1$
would thus hold in
$\mathsf {TT}^1$
would thus hold in
![]() $(M,\mathcal {S})$
and hence in
$(M,\mathcal {S})$
and hence in
![]() $M[X]$
, which cannot be since
$M[X]$
, which cannot be since
![]() $\mathsf {TT}^1$
is true in one but not the other. (Below, we obtain the analogue of this result in the setting of Weihrauch reducibility, but using very different means.)
$\mathsf {TT}^1$
is true in one but not the other. (Below, we obtain the analogue of this result in the setting of Weihrauch reducibility, but using very different means.)
2 Preliminaries
Our computability-theoretic notation is largely standard, following, e.g., Downey and Hirschfeldt [Reference Downey and Hirschfeldt10] and Soare [Reference Soare25]. All objects under discussion are assumed to be represented by elements of
![]() $2^{\omega }$
. To this end, subsets of
$2^{\omega }$
. To this end, subsets of
![]() $\omega $
are identified with their characteristic functions, and elements of
$\omega $
are identified with their characteristic functions, and elements of
![]() $\omega $
are identified with singleton subsets of
$\omega $
are identified with singleton subsets of
![]() $\omega $
. We fix a standard computable bijection between
$\omega $
. We fix a standard computable bijection between
![]() $\omega ^{<\omega }$
and
$\omega ^{<\omega }$
and
![]() $\omega $
such that for all
$\omega $
such that for all
![]() $\alpha \in \omega ^{<\omega }$
,
$\alpha \in \omega ^{<\omega }$
,
![]() $|\alpha |$
is uniformly computable from
$|\alpha |$
is uniformly computable from
![]() $\alpha $
. A subset of
$\alpha $
. A subset of
![]() $\omega ^{<\omega }$
is then identified with its image under this bijection. Finite sets will usually be specified by (and identified with) their canonical indices. More complex representations will be defined as needed.
$\omega ^{<\omega }$
is then identified with its image under this bijection. Finite sets will usually be specified by (and identified with) their canonical indices. More complex representations will be defined as needed.
For subsets
![]() $A_0,\ldots ,A_{n-1}$
of
$A_0,\ldots ,A_{n-1}$
of
![]() $\omega $
(or of
$\omega $
(or of
![]() $\omega ^{<\omega }$
, via our representation) we write
$\omega ^{<\omega }$
, via our representation) we write
![]() $\langle A_0,\ldots ,A_{n-1} \rangle $
instead of the more common
$\langle A_0,\ldots ,A_{n-1} \rangle $
instead of the more common
![]() $A_0 \oplus \cdots \oplus A_{n-1}$
. And given a Turing functional
$A_0 \oplus \cdots \oplus A_{n-1}$
. And given a Turing functional
![]() $\Phi $
, we write
$\Phi $
, we write
![]() $\Phi (A_0,\ldots ,A_{n-1})$
as shorthand for
$\Phi (A_0,\ldots ,A_{n-1})$
as shorthand for
![]() $\Phi ^{\langle A_0,\ldots ,A_{n-1} \rangle }$
.
$\Phi ^{\langle A_0,\ldots ,A_{n-1} \rangle }$
.
The principal object of interest in the framework of Weihrauch-style computable analysis is the following.
Definition 2.1. A instance-solution problem (or just problem) is a partial multifunction
![]() $\mathsf {P} : \subseteq X \rightrightarrows Y$
, where X and Y are subsets of
$\mathsf {P} : \subseteq X \rightrightarrows Y$
, where X and Y are subsets of
![]() $\omega ^\omega $
, such that
$\omega ^\omega $
, such that
![]() $\mathsf {P}(x) \neq \emptyset $
for each
$\mathsf {P}(x) \neq \emptyset $
for each
![]() $x \in \operatorname {dom}(\mathsf {P})$
. The elements of
$x \in \operatorname {dom}(\mathsf {P})$
. The elements of
![]() $\operatorname {dom}(\mathsf {P})$
are called the instances of
$\operatorname {dom}(\mathsf {P})$
are called the instances of
![]() $\mathsf {P}$
(or
$\mathsf {P}$
(or
![]() $\mathsf {P}$
-instances) and for each
$\mathsf {P}$
-instances) and for each
![]() $x \in \operatorname {dom}(\mathsf {P})$
, the elements of
$x \in \operatorname {dom}(\mathsf {P})$
, the elements of
![]() $\mathsf {P}(x)$
are called the solutions to x in
$\mathsf {P}(x)$
are called the solutions to x in
![]() $\mathsf {P}$
(or
$\mathsf {P}$
(or
![]() $\mathsf {P}$
-solutions to x).
$\mathsf {P}$
-solutions to x).
For many principles, there is a natural way to move between their formalization as a statement of second-order arithmetic and as a problem. For example, we can consider the following problem forms of restrictions of
![]() $\mathsf {RT}^1$
and
$\mathsf {RT}^1$
and
![]() $\mathsf {TT}^1$
.
$\mathsf {TT}^1$
.
Definition 2.2. Fix
![]() $k \geq 1$
.
$k \geq 1$
.
-
(1)
 $\mathsf {RT}^1_k$
is the problem whose instances are all colorings
$\mathsf {RT}^1_k$
is the problem whose instances are all colorings
 $f : \omega \to k$
, with the solutions to any such f being all infinite sets
$f : \omega \to k$
, with the solutions to any such f being all infinite sets
 $M \subseteq \omega $
monochromatic for f.
$M \subseteq \omega $
monochromatic for f. -
(2)
 $\mathsf {TT}^1_k$
is the problem whose instances are all colorings
$\mathsf {TT}^1_k$
is the problem whose instances are all colorings
 $f : 2^{<\omega } \to k$
, with the solutions to any such f being all
$f : 2^{<\omega } \to k$
, with the solutions to any such f being all
 $H \cong 2^{<\omega }$
monochromatic for f.
$H \cong 2^{<\omega }$
monochromatic for f.
For
![]() $\mathsf {RT}^1$
and
$\mathsf {RT}^1$
and
![]() $\mathsf {TT}^1$
, there is some subtlety. Brattka and Rakotoniaina [Reference Brattka and Rakotoniaina2, Definition 3.1] considered two problem forms of
$\mathsf {TT}^1$
, there is some subtlety. Brattka and Rakotoniaina [Reference Brattka and Rakotoniaina2, Definition 3.1] considered two problem forms of
![]() $\mathsf {RT}^1$
, denoted by
$\mathsf {RT}^1$
, denoted by
![]() $\mathsf {RT}^1_+$
and
$\mathsf {RT}^1_+$
and
![]() $\mathsf {RT}^1_{\mathbb {N}}$
, which we define next. We define two problem forms of
$\mathsf {RT}^1_{\mathbb {N}}$
, which we define next. We define two problem forms of
![]() $\mathsf {TT}^1$
in an analogous fashion.
$\mathsf {TT}^1$
in an analogous fashion.
Definition 2.3.
-
(1)
 $\mathsf {RT}^1_+$
is the problem whose instances are all pairs
$\mathsf {RT}^1_+$
is the problem whose instances are all pairs
 $\langle k,f \rangle $
where
$\langle k,f \rangle $
where
 $k \geq 1$
and f is a coloring
$k \geq 1$
and f is a coloring
 $\omega \to k$
, with the solutions to any such pair being all infinite sets
$\omega \to k$
, with the solutions to any such pair being all infinite sets
 $M \subseteq \omega $
monochromatic for f.
$M \subseteq \omega $
monochromatic for f. -
(2)
 $\mathsf {RT}^1_{\mathbb {N}}$
is the problem whose instances are all colorings
$\mathsf {RT}^1_{\mathbb {N}}$
is the problem whose instances are all colorings
 $f : \omega \to k$
for some
$f : \omega \to k$
for some
 $k \geq 1$
, with the solutions to any such f being all infinite sets
$k \geq 1$
, with the solutions to any such f being all infinite sets
 $M \subseteq \omega $
monochromatic for f.
$M \subseteq \omega $
monochromatic for f. -
(3)
 $\mathsf {TT}^1_+$
is the problem whose instances are all pairs
$\mathsf {TT}^1_+$
is the problem whose instances are all pairs
 $\langle k,f \rangle $
where
$\langle k,f \rangle $
where
 $k \geq 1$
and f is a coloring
$k \geq 1$
and f is a coloring
 $2^{<\omega } \to k$
, with the solutions to any such pair being all
$2^{<\omega } \to k$
, with the solutions to any such pair being all
 $H \cong 2^{<\omega }$
monochromatic for f.
$H \cong 2^{<\omega }$
monochromatic for f. -
(4)
 $\mathsf {TT}^1_{\mathbb {N}}$
is the problem whose instances are all colorings
$\mathsf {TT}^1_{\mathbb {N}}$
is the problem whose instances are all colorings
 $f : 2^{<\omega } \to k$
for some
$f : 2^{<\omega } \to k$
for some
 $k \geq 1$
, with the solutions to any such f being all
$k \geq 1$
, with the solutions to any such f being all
 $H \cong 2^{<\omega }$
monochromatic for f.
$H \cong 2^{<\omega }$
monochromatic for f.
The distinction here is whether an instance is just a coloring with bounded range, or whether an upper bound must be explicitly provided along with the coloring. From the point of view of a classical system like
![]() $\mathsf {RCA}_0$
, there is no difference between these two formulations. But an upper bound cannot be obtained uniformly computably from a coloring, and this is often useful in constructions—i.e., the ability to increase the number of colors finitely many times while building a coloring without declaring an upper bound in advance. (See, e.g., the proof of Theorem 4.7 below, and see [Reference Dzhafarov and Mummert12, Section 3.3] for a discussion of this and similar issues.) From a purely computability-theoretic perspective, then, the versions
$\mathsf {RCA}_0$
, there is no difference between these two formulations. But an upper bound cannot be obtained uniformly computably from a coloring, and this is often useful in constructions—i.e., the ability to increase the number of colors finitely many times while building a coloring without declaring an upper bound in advance. (See, e.g., the proof of Theorem 4.7 below, and see [Reference Dzhafarov and Mummert12, Section 3.3] for a discussion of this and similar issues.) From a purely computability-theoretic perspective, then, the versions
![]() $\mathsf {RT}^1_{\mathbb {N}}$
and
$\mathsf {RT}^1_{\mathbb {N}}$
and
![]() $\mathsf {TT}^1_{\mathbb {N}}$
are more natural. (For more on the distinction between the
$\mathsf {TT}^1_{\mathbb {N}}$
are more natural. (For more on the distinction between the
![]() $+$
and
$+$
and
![]() $\mathbb {N}$
cases, see the discussion in [Reference Pauly, Pradic and Soldà23].)
$\mathbb {N}$
cases, see the discussion in [Reference Pauly, Pradic and Soldà23].)
Problems can be compared using the following reducibility notion, originally proposed by Weihrauch [Reference Weihrauch28, Reference Weihrauch29], and independently by Dorais, et al. [Reference Dorais, Dzhafarov, Hirst, Mileti and Shafer9] in the guise we use here.
Definition 2.4. Let
![]() $\mathsf {P}$
and
$\mathsf {P}$
and
![]() $\mathsf {Q}$
be problems.
$\mathsf {Q}$
be problems.
-
(1)
 $\mathsf {P}$
is Weihrauch reducible to
$\mathsf {P}$
is Weihrauch reducible to
 $\mathsf {Q}$
, written
$\mathsf {Q}$
, written
 $\mathsf {P} \leq _{\text{W}} \mathsf {Q}$
, if there exist Turing functionals
$\mathsf {P} \leq _{\text{W}} \mathsf {Q}$
, if there exist Turing functionals
 $\Phi $
and
$\Phi $
and
 $\Psi $
such that
$\Psi $
such that
 $\Phi (x) \in \operatorname {dom}(\mathsf {Q})$
for every
$\Phi (x) \in \operatorname {dom}(\mathsf {Q})$
for every
 $x \in \operatorname {dom}(\mathsf {P})$
, and
$x \in \operatorname {dom}(\mathsf {P})$
, and
 $\Psi (x,y) \in \mathsf {P}(x)$
for every
$\Psi (x,y) \in \mathsf {P}(x)$
for every
 $y \in \mathsf {Q}(\Phi (x))$
. In this case, we also say that
$y \in \mathsf {Q}(\Phi (x))$
. In this case, we also say that
 $\mathsf {P}$
is Weihrauch reducible to
$\mathsf {P}$
is Weihrauch reducible to
 $\mathsf {Q}$
via
$\mathsf {Q}$
via
 $\Phi $
and
$\Phi $
and
 $\Psi $
.
$\Psi $
. -
(2) If
 $\mathsf {P} \leq _{\mathrm {W}} \mathsf {Q}$
and
$\mathsf {P} \leq _{\mathrm {W}} \mathsf {Q}$
and
 $\mathsf {Q} \leq _{\mathrm {W}} \mathsf {P}$
then
$\mathsf {Q} \leq _{\mathrm {W}} \mathsf {P}$
then
 $\mathsf {P}$
and
$\mathsf {P}$
and
 $\mathsf {Q}$
are Weihrauch equivalent, written
$\mathsf {Q}$
are Weihrauch equivalent, written
 $\mathsf {P} \equiv _{\mathrm {W}} \mathsf {Q}$
.
$\mathsf {P} \equiv _{\mathrm {W}} \mathsf {Q}$
.
The argument given in Section 1 for
![]() $\mathsf {RT}^1$
being a consequence of
$\mathsf {RT}^1$
being a consequence of
![]() $\mathsf {TT}^1$
directly shows that for all
$\mathsf {TT}^1$
directly shows that for all
![]() $k \geq 1$
,
$k \geq 1$
,
![]() $\mathsf {RT}^1_k \leq _{\mathrm {W}} \mathsf {TT}^1_k$
, that
$\mathsf {RT}^1_k \leq _{\mathrm {W}} \mathsf {TT}^1_k$
, that
![]() $\mathsf {RT}^1_+ \leq _{\mathrm {W}} \mathsf {RT}^1_{\mathbb {N}} \leq _{\mathrm {W}} \mathsf {TT}^1_{\mathbb {N}}$
, and also that
$\mathsf {RT}^1_+ \leq _{\mathrm {W}} \mathsf {RT}^1_{\mathbb {N}} \leq _{\mathrm {W}} \mathsf {TT}^1_{\mathbb {N}}$
, and also that
![]() $\mathsf {RT}^1_+ \leq _{\mathrm {W}} \mathsf {TT}^1_+$
. That none of these reductions can be reversed follows from Theorems 4.4 and 4.7 below. We will continue to use the initialisms
$\mathsf {RT}^1_+ \leq _{\mathrm {W}} \mathsf {TT}^1_+$
. That none of these reductions can be reversed follows from Theorems 4.4 and 4.7 below. We will continue to use the initialisms
![]() $\mathsf {RT}^1$
and
$\mathsf {RT}^1$
and
![]() $\mathsf {TT}^1$
when speaking, generally, about any of the problems from Definitions 2.2 and 2.3.
$\mathsf {TT}^1$
when speaking, generally, about any of the problems from Definitions 2.2 and 2.3.
We now define the notion of the first-order part of a problem, originally introduced by Dzhafarov, Solomon, and Yokoyama [Reference Dzhafarov, Solomon and Yokoyama13, Definition 2.1]. In what follows, Turing functionals are assumed to be represented by their indices within some fixed enumeration of all partial computable oracle functions.
Definition 2.5. Let
![]() $\mathsf {P}$
be a problem. The first-order part of
$\mathsf {P}$
be a problem. The first-order part of
![]() $\mathsf {P}$
, denoted
$\mathsf {P}$
, denoted
![]() ${}^1 \mathsf {P}$
, is the following problem:
${}^1 \mathsf {P}$
, is the following problem:
-
• the instances of
 ${}^1 \mathsf {P}$
are all triples
${}^1 \mathsf {P}$
are all triples
 $\langle A,\Delta ,\Gamma \rangle $
where
$\langle A,\Delta ,\Gamma \rangle $
where
 $A \in 2^\omega $
is arbitrary and
$A \in 2^\omega $
is arbitrary and
 $\Delta $
and
$\Delta $
and
 $\Gamma $
are Turing functionals such that
$\Gamma $
are Turing functionals such that
 $\Delta (A) \in \operatorname {dom}(\mathsf {P})$
and
$\Delta (A) \in \operatorname {dom}(\mathsf {P})$
and
 $\Gamma (A,y)(0) \downarrow $
for all
$\Gamma (A,y)(0) \downarrow $
for all
 $y \in \mathsf {P}(\Delta (A))$
;
$y \in \mathsf {P}(\Delta (A))$
; -
• the solutions to any
 $\langle A,\Delta ,\Gamma \rangle $
as above are all values of the form
$\langle A,\Delta ,\Gamma \rangle $
as above are all values of the form
 $\Gamma (A,y)(0)$
for some
$\Gamma (A,y)(0)$
for some
 $y \in \mathsf {P}(\Delta (A))$
.
$y \in \mathsf {P}(\Delta (A))$
.
Intuitively,
![]() ${}^1 \mathsf {P}$
considers an instance of
${}^1 \mathsf {P}$
considers an instance of
![]() $\mathsf {P}$
along with a functional that halts on an initial segment of any
$\mathsf {P}$
along with a functional that halts on an initial segment of any
![]() $\mathsf {P}$
-solution, and accepts the output of that computation as its own solution. (A slightly different but equivalent formulation appears in [Reference Soldà and Valenti26, Definition 3.1].)
$\mathsf {P}$
-solution, and accepts the output of that computation as its own solution. (A slightly different but equivalent formulation appears in [Reference Soldà and Valenti26, Definition 3.1].)
The reason for the name “first-order” is that, as shown in [Reference Dzhafarov, Solomon and Yokoyama13, Theorem 2.2],
![]() ${}^1 \mathsf {P}$
is Weihrauch equivalent to the maximum under
${}^1 \mathsf {P}$
is Weihrauch equivalent to the maximum under
![]() $\leq _{\mathrm {W}}$
of all
$\leq _{\mathrm {W}}$
of all
![]() $\mathsf {Q} \leq _{\mathrm {W}} \mathsf {P}$
with co-domain
$\mathsf {Q} \leq _{\mathrm {W}} \mathsf {P}$
with co-domain
![]() $\omega $
. Such a problem is called first-order. Thus,
$\omega $
. Such a problem is called first-order. Thus,
![]() ${}^1 \mathsf {P}$
is the “strongest” first-order problem that lies Weihrauch below
${}^1 \mathsf {P}$
is the “strongest” first-order problem that lies Weihrauch below
![]() $\mathsf {P}$
. Using this characterization, we can thus see that for all
$\mathsf {P}$
. Using this characterization, we can thus see that for all
![]() $k \geq 1$
,
$k \geq 1$
,
![]() ${}^1 \mathsf {RT}^1_k \equiv _{\mathrm {W}} \mathsf {RT}^1_k$
, and that
${}^1 \mathsf {RT}^1_k \equiv _{\mathrm {W}} \mathsf {RT}^1_k$
, and that
![]() ${}^1 \mathsf {RT}^1_{+} \equiv _{\mathrm {W}} \mathsf {RT}^1_{+}$
and
${}^1 \mathsf {RT}^1_{+} \equiv _{\mathrm {W}} \mathsf {RT}^1_{+}$
and
![]() ${}^1 \mathsf {RT}^1_{\mathbb {N}} \equiv _{\mathrm {W}} \mathsf {RT}^1_{\mathbb {N}}$
. This is because in each case, knowing the color of an infinite homogeneous for a given coloring suffices to uniformly compute such a set from the coloring. This is not the case for trees, as we will show below. But we do have that for all
${}^1 \mathsf {RT}^1_{\mathbb {N}} \equiv _{\mathrm {W}} \mathsf {RT}^1_{\mathbb {N}}$
. This is because in each case, knowing the color of an infinite homogeneous for a given coloring suffices to uniformly compute such a set from the coloring. This is not the case for trees, as we will show below. But we do have that for all
![]() $k \geq 1$
,
$k \geq 1$
,
![]() $\mathsf {RT}^1_k \leq _{\mathrm {W}} {}^1 \mathsf {TT}^1_k \leq _{\mathrm {W}} \mathsf {TT}^1_k$
; that
$\mathsf {RT}^1_k \leq _{\mathrm {W}} {}^1 \mathsf {TT}^1_k \leq _{\mathrm {W}} \mathsf {TT}^1_k$
; that
![]() $\mathsf {RT}^1_{+} \leq _{\mathrm {W}} {}^1 \mathsf {TT}^1_{+} \leq _{\mathrm {W}} \mathsf {TT}^1_{+}$
; and that
$\mathsf {RT}^1_{+} \leq _{\mathrm {W}} {}^1 \mathsf {TT}^1_{+} \leq _{\mathrm {W}} \mathsf {TT}^1_{+}$
; and that
![]() $\mathsf {RT}^1_{\mathbb {N}} \leq _{\mathrm {W}} {}^1 \mathsf {TT}^1_{\mathbb {N}} \leq _{\mathrm {W}} \mathsf {TT}^1_{\mathbb {N}}$
.
$\mathsf {RT}^1_{\mathbb {N}} \leq _{\mathrm {W}} {}^1 \mathsf {TT}^1_{\mathbb {N}} \leq _{\mathrm {W}} \mathsf {TT}^1_{\mathbb {N}}$
.
We conclude this section with some definitions specific to our working with elements and subset of
![]() $2^{<\omega }$
.
$2^{<\omega }$
.
Definition 2.6. Fix
![]() $S \subseteq 2^{<\omega }$
.
$S \subseteq 2^{<\omega }$
.
-
(1) The rank of
 $\sigma \in S$
in S, denoted
$\sigma \in S$
in S, denoted
 $\mathrm {rk}_S(\sigma )$
, is
$\mathrm {rk}_S(\sigma )$
, is
 $|\{ \tau \in S : \tau \prec \sigma \}|$
.
$|\{ \tau \in S : \tau \prec \sigma \}|$
. -
(2) For
 $n \in \omega $
,
$n \in \omega $
,
 $S^{\mathrm {rk} < n}$
denotes the set
$S^{\mathrm {rk} < n}$
denotes the set
 $\{ \sigma \in S : \mathrm {rk}_S(\sigma ) < n \}$
.
$\{ \sigma \in S : \mathrm {rk}_S(\sigma ) < n \}$
. -
(3) S is rooted if it there is a unique
 $\rho \in S$
, called the root of S, with
$\rho \in S$
, called the root of S, with
 $\mathrm {rk}_S(\rho ) = 0$
.
$\mathrm {rk}_S(\rho ) = 0$
. -
(4)
 $\tau \in S$
is a successor of
$\tau \in S$
is a successor of
 $\sigma \in S$
in S if
$\sigma \in S$
in S if
 $\sigma \prec \tau $
and
$\sigma \prec \tau $
and
 $\mathrm {rk}_S(\tau ) = \mathrm {rk}_S(\sigma )+1$
.
$\mathrm {rk}_S(\tau ) = \mathrm {rk}_S(\sigma )+1$
. -
(5)
 $\sigma \in S$
is a leaf of S if it has no successor in S.
$\sigma \in S$
is a leaf of S if it has no successor in S. -
(6) S is symmetric if all
 $\sigma ,\tau \in S$
with
$\sigma ,\tau \in S$
with
 $\mathrm {rk}_S(\sigma ) = \mathrm {rk}_S(\tau )$
have the same number of successors in S.
$\mathrm {rk}_S(\sigma ) = \mathrm {rk}_S(\tau )$
have the same number of successors in S. -
(7) The height of S, denoted
 $\mathrm {ht}(S)$
, is
$\mathrm {ht}(S)$
, is
 $\sup \{ \mathrm {rk}_S(\sigma ) + 1 : \sigma \in S \}$
. (So
$\sup \{ \mathrm {rk}_S(\sigma ) + 1 : \sigma \in S \}$
. (So
 $\mathrm {ht}(\emptyset ) = 0$
.)
$\mathrm {ht}(\emptyset ) = 0$
.)
For all oracles A, we assume that if
![]() $\Phi (A)(n) \downarrow $
then
$\Phi (A)(n) \downarrow $
then
![]() $\Phi (A)(m) \downarrow $
for all
$\Phi (A)(m) \downarrow $
for all
![]() $m < n$
. We also adopt the following more specific conventions about oracles contained in
$m < n$
. We also adopt the following more specific conventions about oracles contained in
![]() $2^{<\omega }$
. If
$2^{<\omega }$
. If
![]() $\Phi $
is a functional and
$\Phi $
is a functional and
![]() $S \subseteq 2^{<\omega }$
is a finite set such that
$S \subseteq 2^{<\omega }$
is a finite set such that
![]() $\Phi (S)(n) \downarrow $
for some n, then we assume the length of the computation is bounded by the length of the shortest leaf in S. This ensures that if
$\Phi (S)(n) \downarrow $
for some n, then we assume the length of the computation is bounded by the length of the shortest leaf in S. This ensures that if
![]() $T \subseteq 2^{<\omega }$
is any set (finite or infinite) such that
$T \subseteq 2^{<\omega }$
is any set (finite or infinite) such that
![]() $T \supseteq S$
and every
$T \supseteq S$
and every
![]() $\sigma \in T \setminus S$
extends a leaf of S, then
$\sigma \in T \setminus S$
extends a leaf of S, then
![]() $\Phi (T)(n) \downarrow = \Phi (S)(n)$
. More generally, we have that if
$\Phi (T)(n) \downarrow = \Phi (S)(n)$
. More generally, we have that if
![]() $\varphi (X)$
is any
$\varphi (X)$
is any
![]() $\Sigma ^0_1$
formula such that
$\Sigma ^0_1$
formula such that
![]() $\varphi (S)$
holds, then so does
$\varphi (S)$
holds, then so does
![]() $\varphi (T)$
.
$\varphi (T)$
.
Unless otherwise noted, all objects throughout should be regarded as elements of
![]() $\omega ^{\omega }$
via standard codings.
$\omega ^{\omega }$
via standard codings.
3 The complexity of building monochromatic solutions
An initial point of distinction between the complexities of
![]() $\mathsf {RT}^1$
and
$\mathsf {RT}^1$
and
![]() $\mathsf {TT}^1$
can be seen in the complexity of checking whether a given set is a solution to a given coloring, versus whether a given element is extendible to a solution. It is easy to see that for
$\mathsf {TT}^1$
can be seen in the complexity of checking whether a given set is a solution to a given coloring, versus whether a given element is extendible to a solution. It is easy to see that for
![]() $\mathsf {RT}^1$
, both questions are
$\mathsf {RT}^1$
, both questions are
![]() $\Pi ^0_2$
relative to the set and the coloring. For
$\Pi ^0_2$
relative to the set and the coloring. For
![]() $\mathsf {TT}^1$
, checking whether a given set is a solution is likewise
$\mathsf {TT}^1$
, checking whether a given set is a solution is likewise
![]() $\Pi ^0_2$
: indeed, saying that H is monochromatic for a given
$\Pi ^0_2$
: indeed, saying that H is monochromatic for a given
![]() $\mathsf {TT}^1$
instance f is
$\mathsf {TT}^1$
instance f is
![]() $\Pi ^0_1$
in H and f, while saying that
$\Pi ^0_1$
in H and f, while saying that
![]() $H \cong 2^{<\omega }$
can be expressed as
$H \cong 2^{<\omega }$
can be expressed as
 $$ \begin{align*} &H \neq \emptyset \wedge (\forall \sigma \in H)(\exists \tau_0,\tau_1 \in H)[\sigma \prec \tau_0,\tau_1 \wedge \tau_0 \mid \tau_1]\hspace{5em}\\ \wedge (\forall \sigma \in H)&(\forall \tau_0,\tau_1,\tau_2 \in H)[\sigma \prec \tau_0,\tau_1,\tau_2 \to (\exists \rho \in H)(\exists i < 3)[\sigma \prec \rho \prec \tau_i]]. \end{align*} $$
$$ \begin{align*} &H \neq \emptyset \wedge (\forall \sigma \in H)(\exists \tau_0,\tau_1 \in H)[\sigma \prec \tau_0,\tau_1 \wedge \tau_0 \mid \tau_1]\hspace{5em}\\ \wedge (\forall \sigma \in H)&(\forall \tau_0,\tau_1,\tau_2 \in H)[\sigma \prec \tau_0,\tau_1,\tau_2 \to (\exists \rho \in H)(\exists i < 3)[\sigma \prec \rho \prec \tau_i]]. \end{align*} $$
However, in stark contrast, whether or not an element of
![]() $2^{<\omega }$
is part of a solution to a given instance of
$2^{<\omega }$
is part of a solution to a given instance of
![]() $\mathsf {TT}^1$
is far harder: it is
$\mathsf {TT}^1$
is far harder: it is
![]() $\Sigma ^1_1$
-complete relative to H and f. We can express this using Weihrauch reducibility using the definition below. As a canonical representative of a “
$\Sigma ^1_1$
-complete relative to H and f. We can express this using Weihrauch reducibility using the definition below. As a canonical representative of a “
![]() $\Sigma ^1_1$
-complete problem” we take
$\Sigma ^1_1$
-complete problem” we take
![]() $\mathsf {WF}$
, which we recall is the problem whose instances are arbitrary trees
$\mathsf {WF}$
, which we recall is the problem whose instances are arbitrary trees
![]() $T \subseteq \omega ^{<\omega }$
, with the solution to any such T being
$T \subseteq \omega ^{<\omega }$
, with the solution to any such T being
![]() $0$
or
$0$
or
![]() $1$
depending as T is ill-founded or well-founded, respectively.
$1$
depending as T is ill-founded or well-founded, respectively.
Definition 3.1. Fix
![]() $k \geq 1$
.
$k \geq 1$
.
![]() $\mathsf {TT}^1_k$
-
$\mathsf {TT}^1_k$
-
![]() $\mathsf {Ext}$
is the problem whose instances are pairs
$\mathsf {Ext}$
is the problem whose instances are pairs
![]() $\langle f,\sigma \rangle $
where f is a coloring
$\langle f,\sigma \rangle $
where f is a coloring
![]() $2^{<\omega } \to k$
and
$2^{<\omega } \to k$
and
![]() $\sigma \in 2^{<\omega }$
, with the solutions to any such pair being
$\sigma \in 2^{<\omega }$
, with the solutions to any such pair being
![]() $1$
or
$1$
or
![]() $0$
depending as there is or is not an
$0$
depending as there is or is not an
![]() $H \cong 2^{<\omega }$
monochromatic for f and containing
$H \cong 2^{<\omega }$
monochromatic for f and containing
![]() $\sigma $
.
$\sigma $
.
Theorem 3.2. For all
![]() $k \geq 2$
,
$k \geq 2$
,
![]() $\mathsf {TT}^1_k$
-
$\mathsf {TT}^1_k$
-
![]() $\mathsf {Ext} \equiv _{\mathrm {W}} \mathsf {WF}$
.
$\mathsf {Ext} \equiv _{\mathrm {W}} \mathsf {WF}$
.
Proof. The reduction from
![]() $\mathsf {TT}^1_k$
-
$\mathsf {TT}^1_k$
-
![]() $\mathsf {Ext}$
to
$\mathsf {Ext}$
to
![]() $\mathsf {WF}$
is straightforward. Given an instance
$\mathsf {WF}$
is straightforward. Given an instance
![]() $\langle f,\sigma \rangle $
of the former, checking whether there exists
$\langle f,\sigma \rangle $
of the former, checking whether there exists
![]() $H \cong 2^{<\omega }$
monochromatic for f and containing
$H \cong 2^{<\omega }$
monochromatic for f and containing
![]() $\sigma $
as an initial segment is a uniformly
$\sigma $
as an initial segment is a uniformly
![]() $\Sigma ^1_1$
property in f and
$\Sigma ^1_1$
property in f and
![]() $\sigma $
, and thus can be decided using
$\sigma $
, and thus can be decided using
![]() $\mathsf {WF}$
.
$\mathsf {WF}$
.
In the other direction, let
![]() $T \subseteq \omega ^{<\omega }$
be a tree. We define a uniformly T-computable coloring
$T \subseteq \omega ^{<\omega }$
be a tree. We define a uniformly T-computable coloring
![]() $f : 2^{<\omega } \to 2$
with
$f : 2^{<\omega } \to 2$
with
![]() $f(\langle \rangle ) = 0$
and such that T is well-founded if and only if there is no
$f(\langle \rangle ) = 0$
and such that T is well-founded if and only if there is no
![]() $H \cong 2^{<\omega }$
monochromatic for f with color
$H \cong 2^{<\omega }$
monochromatic for f with color
![]() $0$
. Thus, T is well-founded if and only if the
$0$
. Thus, T is well-founded if and only if the
![]() $\mathsf {TT}^1_2$
-
$\mathsf {TT}^1_2$
-
![]() $\mathsf {Ext}$
-solution to
$\mathsf {Ext}$
-solution to
![]() $\langle f,\{ \langle \rangle \} \rangle $
is
$\langle f,\{ \langle \rangle \} \rangle $
is
![]() $0$
. Define
$0$
. Define
![]() $S = T * \omega ^{<\omega } = \{ \langle \alpha ,\beta \rangle : \alpha \in T, \beta \in \omega ^{<\omega },|\alpha |=|\beta | \}$
, viewed as a subtree of
$S = T * \omega ^{<\omega } = \{ \langle \alpha ,\beta \rangle : \alpha \in T, \beta \in \omega ^{<\omega },|\alpha |=|\beta | \}$
, viewed as a subtree of
![]() $\omega ^{<\omega }$
by thinking of
$\omega ^{<\omega }$
by thinking of
![]() $\langle \alpha ,\beta \rangle $
as a prefix of
$\langle \alpha ,\beta \rangle $
as a prefix of
![]() $\langle \alpha ',\beta ' \rangle $
if and only if
$\langle \alpha ',\beta ' \rangle $
if and only if
![]() $\alpha \preceq \alpha '$
and
$\alpha \preceq \alpha '$
and
![]() $\beta \preceq \beta '$
. Observe that
$\beta \preceq \beta '$
. Observe that
![]() $[T] \neq \emptyset $
if and only if
$[T] \neq \emptyset $
if and only if
![]() $|[S]| = 2^{\aleph _0}$
. Let R be the collection of all strings of the form
$|[S]| = 2^{\aleph _0}$
. Let R be the collection of all strings of the form
![]() $0^{\gamma (0)}10^{\gamma (1)}1\cdots 0^{\gamma (|\gamma |-1)}1 0^s$
for some
$0^{\gamma (0)}10^{\gamma (1)}1\cdots 0^{\gamma (|\gamma |-1)}1 0^s$
for some
![]() $\gamma \in S$
and some
$\gamma \in S$
and some
![]() $s \in \omega $
. Then R is a T-computable subtree of
$s \in \omega $
. Then R is a T-computable subtree of
![]() $2^{<\omega }$
, and we have
$2^{<\omega }$
, and we have
![]() $\langle \rangle \in R$
. Although
$\langle \rangle \in R$
. Although
![]() $[R]$
is non-empty (since it contains, at the very least, the constantly
$[R]$
is non-empty (since it contains, at the very least, the constantly
![]() $0$
function) we have that
$0$
function) we have that
![]() $|[R]| = 2^{\aleph _0}$
if and only if
$|[R]| = 2^{\aleph _0}$
if and only if
![]() $|[S]| = 2^{\aleph _0}$
. We define f by setting
$|[S]| = 2^{\aleph _0}$
. We define f by setting
![]() $f(\sigma ) = 0$
if
$f(\sigma ) = 0$
if
![]() $\sigma \in R$
and
$\sigma \in R$
and
![]() $f(\sigma ) = 1$
if
$f(\sigma ) = 1$
if
![]() $\sigma \notin R$
. Thus
$\sigma \notin R$
. Thus
![]() $f(\langle \rangle ) = 0$
, and there exists
$f(\langle \rangle ) = 0$
, and there exists
![]() $H \cong 2^{<\omega }$
monochromatic for f and containing
$H \cong 2^{<\omega }$
monochromatic for f and containing
![]() $\langle \rangle $
if and only if there exists a
$\langle \rangle $
if and only if there exists a
![]() $H \cong 2^{<\omega }$
monochromatic for f with color
$H \cong 2^{<\omega }$
monochromatic for f with color
![]() $0$
, which in turn holds in if and only if
$0$
, which in turn holds in if and only if
![]() $|[R]| = 2^{\aleph _0}$
, which, by our previous observations, holds if and only if
$|[R]| = 2^{\aleph _0}$
, which, by our previous observations, holds if and only if
![]() $[T] \neq \emptyset $
. This completes the proof.
$[T] \neq \emptyset $
. This completes the proof.
The theorem highlights the intrinsic complexity of knowing whether a given instance of
![]() $\mathsf {TT}^1$
admits a solution of a particular, fixed color. In the “dense-or-cone” proof of
$\mathsf {TT}^1$
admits a solution of a particular, fixed color. In the “dense-or-cone” proof of
![]() $\mathsf {TT}^1$
discussed in Section 1, deciding the color in which to try to build a solution was handled by asking certain density questions about the coloring. In an attempt to better understand this, we now look at several variants of the “dense-or-cone” argument, and investigate how they relate. Although our discussion could be made more general, and apply to
$\mathsf {TT}^1$
discussed in Section 1, deciding the color in which to try to build a solution was handled by asking certain density questions about the coloring. In an attempt to better understand this, we now look at several variants of the “dense-or-cone” argument, and investigate how they relate. Although our discussion could be made more general, and apply to
![]() $\mathsf {TT}^1$
for arbitrary numbers of colors, we restrict our discussion to
$\mathsf {TT}^1$
for arbitrary numbers of colors, we restrict our discussion to
![]() $2$
-colorings. Our goal is not to obtain a complete classification of these problems, which are not overly interesting in their own, but rather to get a sense of the relationships between different approaches to solving
$2$
-colorings. Our goal is not to obtain a complete classification of these problems, which are not overly interesting in their own, but rather to get a sense of the relationships between different approaches to solving
![]() $\mathsf {TT}^1$
, as a heuristic for our work moving forward.
$\mathsf {TT}^1$
, as a heuristic for our work moving forward.
Definition 3.3. We define the following problems. Each has as its set of instances all
![]() $2$
-colorings of
$2$
-colorings of
![]() $2^{<\omega }$
. Thus, we specify a problem by the set of solutions to a given such coloring
$2^{<\omega }$
. Thus, we specify a problem by the set of solutions to a given such coloring
![]() $f : 2^{<\omega } \to 2$
.
$f : 2^{<\omega } \to 2$
.
-
•
 $\mathsf {V}_{0}$
: The solutions to f are all pairs
$\mathsf {V}_{0}$
: The solutions to f are all pairs
 $\langle i,\sigma \rangle \in 2 \times 2^{<\omega }$
such that
$\langle i,\sigma \rangle \in 2 \times 2^{<\omega }$
such that
 $\{ \tau : f(\tau ) = i \}$
is dense above
$\{ \tau : f(\tau ) = i \}$
is dense above
 $\sigma $
.
$\sigma $
. -
•
 $\mathsf {V}_{1}$
: The solutions to f are all pairs
$\mathsf {V}_{1}$
: The solutions to f are all pairs
 $\langle i,\sigma \rangle \in 2 \times 2^{<\omega }$
such that either
$\langle i,\sigma \rangle \in 2 \times 2^{<\omega }$
such that either
 $\{ \tau : f(\tau ) = 0 \}$
and
$\{ \tau : f(\tau ) = 0 \}$
and
 $\{ \tau : f(\tau ) = 1 \}$
are both dense, or
$\{ \tau : f(\tau ) = 1 \}$
are both dense, or
 $f(\tau ) = i$
for all
$f(\tau ) = i$
for all
 $\tau \succeq \sigma $
.
$\tau \succeq \sigma $
. -
•
 $\mathsf {V}_{2}$
: The solutions to f are all pairs
$\mathsf {V}_{2}$
: The solutions to f are all pairs
 $\langle i,\sigma \rangle $
such that if
$\langle i,\sigma \rangle $
such that if
 $i = 0$
then
$i = 0$
then
 $\{ \tau : f(\tau ) = 0 \}$
is dense, and if
$\{ \tau : f(\tau ) = 0 \}$
is dense, and if
 $i = 1$
then
$i = 1$
then
 $\{ \tau : f(\tau ) = 1 \}$
is dense above
$\{ \tau : f(\tau ) = 1 \}$
is dense above
 $\sigma $
.
$\sigma $
. -
•
 $\mathsf {V}_{3}$
: The solutions to f are all pairs
$\mathsf {V}_{3}$
: The solutions to f are all pairs
 $\langle i,\sigma \rangle $
such that if
$\langle i,\sigma \rangle $
such that if
 $i = 0$
then
$i = 0$
then
 $\{ \tau : f(\tau ) = 0 \}$
is dense, and if
$\{ \tau : f(\tau ) = 0 \}$
is dense, and if
 $i = 1$
then all
$i = 1$
then all
 $\tau \succeq \sigma $
with
$\tau \succeq \sigma $
with
 $f(\tau ) = 0$
are comparable.
$f(\tau ) = 0$
are comparable. -
•
 $\mathsf {V}_{4}$
: The solutions to f are all pairs
$\mathsf {V}_{4}$
: The solutions to f are all pairs
 $\langle i,\sigma \rangle $
such that if
$\langle i,\sigma \rangle $
such that if
 $i = 0$
then
$i = 0$
then
 $\{ \tau : f(\tau ) = 0 \}$
is dense, and if
$\{ \tau : f(\tau ) = 0 \}$
is dense, and if
 $i = 1$
then
$i = 1$
then
 $f(\tau ) = 1$
for all
$f(\tau ) = 1$
for all
 $\tau \succeq \sigma $
.
$\tau \succeq \sigma $
.
It is clear from the definitions that
![]() $\mathsf {TT}^1_2 \leq _{\mathrm {W}} \mathsf {V}_{0} \leq _{\mathrm {W}} \mathsf {V}_{1}$
and that
$\mathsf {TT}^1_2 \leq _{\mathrm {W}} \mathsf {V}_{0} \leq _{\mathrm {W}} \mathsf {V}_{1}$
and that
![]() $\mathsf {V}_{2} \leq _{\mathrm {W}} \mathsf {V}_{3} \leq _{\mathrm {W}} \mathsf {V}_{4}$
. A bit less straightforward is that also
$\mathsf {V}_{2} \leq _{\mathrm {W}} \mathsf {V}_{3} \leq _{\mathrm {W}} \mathsf {V}_{4}$
. A bit less straightforward is that also
![]() $\mathsf {V}_{1} \leq _{\mathrm {W}} \mathsf {V}_{2}$
, which follows from Propositions 3.6 and 3.7 below. The purpose of this section is to examine the remaining reductions between these problems. In fact, we prove the following theorem.
$\mathsf {V}_{1} \leq _{\mathrm {W}} \mathsf {V}_{2}$
, which follows from Propositions 3.6 and 3.7 below. The purpose of this section is to examine the remaining reductions between these problems. In fact, we prove the following theorem.
Theorem 3.4.
![]() $\mathsf {TT}^1_2 <_{\mathrm {W}} \mathsf {V}_{0} \equiv _{\mathrm {W}} \mathsf {V}_{1} <_{\mathrm {W}} \mathsf {V}_{2} \equiv _{\mathrm {W}} \mathsf {V}_{3} \equiv _{\mathrm {W}} \mathsf {V}_{4}$
.
$\mathsf {TT}^1_2 <_{\mathrm {W}} \mathsf {V}_{0} \equiv _{\mathrm {W}} \mathsf {V}_{1} <_{\mathrm {W}} \mathsf {V}_{2} \equiv _{\mathrm {W}} \mathsf {V}_{3} \equiv _{\mathrm {W}} \mathsf {V}_{4}$
.
More precisely, we classify
![]() $\mathsf {V}_{0}$
and
$\mathsf {V}_{0}$
and
![]() $\mathsf {V}_{1}$
, and
$\mathsf {V}_{1}$
, and
![]() $\mathsf {V}_{2}, \mathsf {V}_{3}$
, and
$\mathsf {V}_{2}, \mathsf {V}_{3}$
, and
![]() $\mathsf {V}_{4}$
, in terms of previously studied problems from the computable analysis literature. We begin by recalling their definitions. Throughout the following, we think of an arbitrary
$\mathsf {V}_{4}$
, in terms of previously studied problems from the computable analysis literature. We begin by recalling their definitions. Throughout the following, we think of an arbitrary
![]() $\mathbf {\Pi }^0_1$
subset A of
$\mathbf {\Pi }^0_1$
subset A of
![]() $\omega $
as being represented by an enumeration of its complement, which we take to be a total function
$\omega $
as being represented by an enumeration of its complement, which we take to be a total function
![]() $e : \omega \to \omega $
such that
$e : \omega \to \omega $
such that
![]() $\overline {A} = \{ x : x+1 \in \operatorname {ran}(e) \}$
. (Thus,
$\overline {A} = \{ x : x+1 \in \operatorname {ran}(e) \}$
. (Thus,
![]() $\operatorname {ran}(e) = \{ 0 \}$
if and only if
$\operatorname {ran}(e) = \{ 0 \}$
if and only if
![]() $A = \omega $
.)
$A = \omega $
.)
Definition 3.5. We define the following problems.
-
(1) Closed choice on
 $\mathbb {N}$
(
$\mathbb {N}$
(
 $\mathsf {C}_{\mathbb {N}}$
) is the problem whose instances are all non-empty
$\mathsf {C}_{\mathbb {N}}$
) is the problem whose instances are all non-empty
 $\mathbf {\Pi }^0_1$
subsets A of
$\mathbf {\Pi }^0_1$
subsets A of
 $\omega $
, with the solutions to any such A being all
$\omega $
, with the solutions to any such A being all
 $x \in A$
.
$x \in A$
. -
(2) The total continuation of
 $\mathsf {C}_{\mathbb {N}}$
(
$\mathsf {C}_{\mathbb {N}}$
(
 $\mathsf {TC}_{\mathbb {N}}$
) is the problem whose instances are all
$\mathsf {TC}_{\mathbb {N}}$
) is the problem whose instances are all
 $\mathbf {\Pi }^0_1$
subsets A of
$\mathbf {\Pi }^0_1$
subsets A of
 $\omega $
, with the solutions to any such A being all
$\omega $
, with the solutions to any such A being all
 $x \in \omega $
if
$x \in \omega $
if
 $A = \emptyset $
, and all
$A = \emptyset $
, and all
 $x \in A$
otherwise.
$x \in A$
otherwise. -
(3) The strong total continuation of
 $\mathsf {C}_{\mathbb {N}}$
(
$\mathsf {C}_{\mathbb {N}}$
(
 $\mathsf {sTC}_{\mathbb {N}}$
) is the problem whose instances are all
$\mathsf {sTC}_{\mathbb {N}}$
) is the problem whose instances are all
 $\mathbf {\Pi }^0_1$
subsets A of
$\mathbf {\Pi }^0_1$
subsets A of
 $\omega $
, with the solutions to any such A being
$\omega $
, with the solutions to any such A being
 $-1$
if
$-1$
if
 $A = \emptyset $
, and all
$A = \emptyset $
, and all
 $x \in A$
otherwise.
$x \in A$
otherwise.
A full account of closed choice problems is given by Brattka, Gherardi, and Pauly [Reference Brattka, Gherardi and Pauly1, Section 7]. The total continuation of closed choice was first studied by Neumann and Pauly [Reference Neumann and Pauly21]. The strong total continuation, as a general operator on problems, was introduced more recently, by Marcone and Valenti [Reference Marcone and Valenti20, Definition 4.17]. The difference between
![]() $\mathsf {C}_{\mathbb {N}}$
and
$\mathsf {C}_{\mathbb {N}}$
and
![]() $\mathsf {TC}_{\mathbb {N}}$
is that the latter problem is also defined on the empty set, while the former is not. The difference between
$\mathsf {TC}_{\mathbb {N}}$
is that the latter problem is also defined on the empty set, while the former is not. The difference between
![]() $\mathsf {TC}_{\mathbb {N}}$
and
$\mathsf {TC}_{\mathbb {N}}$
and
![]() $\mathsf {sTC}_{\mathbb {N}}$
is that the latter must indicate, as part of its solution, whether or not the instance it is solving is the empty set, while the former need not do so.
$\mathsf {sTC}_{\mathbb {N}}$
is that the latter must indicate, as part of its solution, whether or not the instance it is solving is the empty set, while the former need not do so.
Proposition 3.6.
![]() $\mathsf {V}_{0} \equiv _{\mathrm {W}} \mathsf {V}_{1} \equiv _{\mathrm {W}} \mathsf {TC}_{\mathbb {N}}$
.
$\mathsf {V}_{0} \equiv _{\mathrm {W}} \mathsf {V}_{1} \equiv _{\mathrm {W}} \mathsf {TC}_{\mathbb {N}}$
.
Proof. As already noted,
![]() $\mathsf {V}_{0} \leq _{\mathrm {W}} \mathsf {V}_{1}$
. It thus remains to show that
$\mathsf {V}_{0} \leq _{\mathrm {W}} \mathsf {V}_{1}$
. It thus remains to show that
![]() $\mathsf {V}_{1} \leq _{\mathrm {W}} \mathsf {TC}_{\mathbb {N}} \leq _{\mathrm {W}} \mathsf {V}_{0}$
. To see that
$\mathsf {V}_{1} \leq _{\mathrm {W}} \mathsf {TC}_{\mathbb {N}} \leq _{\mathrm {W}} \mathsf {V}_{0}$
. To see that
![]() $\mathsf {V}_{1} \leq _{\mathrm {W}} \mathsf {TC}_{\mathbb {N}}$
, fix any instance
$\mathsf {V}_{1} \leq _{\mathrm {W}} \mathsf {TC}_{\mathbb {N}}$
, fix any instance
![]() $f : 2^{<\omega } \to 2$
of
$f : 2^{<\omega } \to 2$
of
![]() $\mathsf {V}_{1}$
. Consider the
$\mathsf {V}_{1}$
. Consider the
![]() $\Pi ^{0,f}_1$
set
$\Pi ^{0,f}_1$
set
![]() $A = \{ \langle i,\sigma \rangle : (\forall \tau \succeq \sigma )[f(\tau ) = i] \}$
, regarded as an instance of
$A = \{ \langle i,\sigma \rangle : (\forall \tau \succeq \sigma )[f(\tau ) = i] \}$
, regarded as an instance of
![]() $\mathsf {TC}_{\mathbb {N}}$
uniformly computable from f. Clearly,
$\mathsf {TC}_{\mathbb {N}}$
uniformly computable from f. Clearly,
![]() $A \neq \emptyset $
if and only if
$A \neq \emptyset $
if and only if
![]() $\{ \tau : f(\tau ) = 0 \}$
and
$\{ \tau : f(\tau ) = 0 \}$
and
![]() $\{ \tau : f(\tau ) = 1 \}$
are not both dense. Thus, any
$\{ \tau : f(\tau ) = 1 \}$
are not both dense. Thus, any
![]() $\mathsf {TC}_{\mathbb {N}}$
-solution to A is a
$\mathsf {TC}_{\mathbb {N}}$
-solution to A is a
![]() $\mathsf {V}_{1}$
-solution to f.
$\mathsf {V}_{1}$
-solution to f.
To conclude the proof, we show that
![]() $\mathsf {TC}_{\mathbb {N}} \leq _{\mathrm {W}} \mathsf {V}_{0}$
. Fix an instance A of
$\mathsf {TC}_{\mathbb {N}} \leq _{\mathrm {W}} \mathsf {V}_{0}$
. Fix an instance A of
![]() $\mathsf {TC}_{\mathbb {N}}$
, specified by a co-enumeration
$\mathsf {TC}_{\mathbb {N}}$
, specified by a co-enumeration
![]() $e : \omega \to \omega $
. From e we can uniformly compute the function
$e : \omega \to \omega $
. From e we can uniformly compute the function
![]() $\ell : \omega \to \omega $
such that
$\ell : \omega \to \omega $
such that
![]() $\ell (s) = (\mu x)[x+1 \notin e \operatorname {\mathrm {\upharpoonright }} s]$
. Clearly,
$\ell (s) = (\mu x)[x+1 \notin e \operatorname {\mathrm {\upharpoonright }} s]$
. Clearly,
![]() $A \neq \emptyset $
if and only if
$A \neq \emptyset $
if and only if
![]() $\lim _s \ell (s)$
exists, in which case
$\lim _s \ell (s)$
exists, in which case
![]() $\lim _s \ell (s) \in A$
. We now define a uniformly e-computable coloring
$\lim _s \ell (s) \in A$
. We now define a uniformly e-computable coloring
![]() $f : 2^{<\omega } \to 2$
, as follows. Let
$f : 2^{<\omega } \to 2$
, as follows. Let
![]() $f(\langle \rangle ) = 0$
, and for each
$f(\langle \rangle ) = 0$
, and for each
![]() $s \in \omega $
, each string
$s \in \omega $
, each string
![]() $\sigma $
of length s, and each
$\sigma $
of length s, and each
![]() $i < 2$
let
$i < 2$
let
 $$\begin{align*}f(\sigma i) = \begin{cases} i & \text{if } \ell(s) \neq \ell(s+1),\\ f(\sigma) & \text{otherwise}. \end{cases} \end{align*}$$
$$\begin{align*}f(\sigma i) = \begin{cases} i & \text{if } \ell(s) \neq \ell(s+1),\\ f(\sigma) & \text{otherwise}. \end{cases} \end{align*}$$
Now, let
![]() $\langle i,\sigma \rangle $
be any
$\langle i,\sigma \rangle $
be any
![]() $\mathsf {V}_{0}$
-solution to f. We claim that
$\mathsf {V}_{0}$
-solution to f. We claim that
![]() $\ell (|\sigma |)$
is a
$\ell (|\sigma |)$
is a
![]() $\mathsf {TC}_{\mathbb {N}}$
-solution to A. Indeed, suppose
$\mathsf {TC}_{\mathbb {N}}$
-solution to A. Indeed, suppose
![]() $A \neq \emptyset $
and fix the least s such that
$A \neq \emptyset $
and fix the least s such that
![]() $\ell (s) = \ell (t)$
for all
$\ell (s) = \ell (t)$
for all
![]() $t \geq s$
. If
$t \geq s$
. If
![]() $|\sigma | < s$
, then it follows from the definition of f that neither
$|\sigma | < s$
, then it follows from the definition of f that neither
![]() $\{ \tau : f(\tau ) = 0 \}$
nor
$\{ \tau : f(\tau ) = 0 \}$
nor
![]() $\{ \tau : f(\tau ) = 1 \}$
is dense above
$\{ \tau : f(\tau ) = 1 \}$
is dense above
![]() $\sigma $
, even though we assumed
$\sigma $
, even though we assumed
![]() $\{ \tau : f(\tau ) = i \}$
is. Thus,
$\{ \tau : f(\tau ) = i \}$
is. Thus,
![]() $|\sigma | \geq s$
, which proves the claim.
$|\sigma | \geq s$
, which proves the claim.
Proposition 3.7.
![]() $\mathsf {V}_{2} \equiv _{\mathrm {W}} \mathsf {V}_{3} \equiv _{\mathrm {W}} \mathsf {V}_{4} \equiv _{\mathrm {W}} \mathsf {sTC}_{\mathbb {N}}$
.
$\mathsf {V}_{2} \equiv _{\mathrm {W}} \mathsf {V}_{3} \equiv _{\mathrm {W}} \mathsf {V}_{4} \equiv _{\mathrm {W}} \mathsf {sTC}_{\mathbb {N}}$
.
Proof. As already mentioned,
![]() $\mathsf {V}_{2} \leq _{\mathrm {W}} \mathsf {V}_{3} \leq _{\mathrm {W}} \mathsf {V}_{4}$
, so we have only to show that
$\mathsf {V}_{2} \leq _{\mathrm {W}} \mathsf {V}_{3} \leq _{\mathrm {W}} \mathsf {V}_{4}$
, so we have only to show that
![]() $\mathsf {V}_{4} \leq _{\mathrm {W}} \mathsf {sTC}_{\mathbb {N}} \leq _{\mathrm {W}} \mathsf {V}_{2}$
. For the first reduction, fix
$\mathsf {V}_{4} \leq _{\mathrm {W}} \mathsf {sTC}_{\mathbb {N}} \leq _{\mathrm {W}} \mathsf {V}_{2}$
. For the first reduction, fix
![]() $f : 2^{<\omega } \to 2$
and define
$f : 2^{<\omega } \to 2$
and define
![]() $A = \{ \sigma : (\forall \tau \succeq \sigma )[f(\tau ) = 1] \}$
. We can regard A as an instance of
$A = \{ \sigma : (\forall \tau \succeq \sigma )[f(\tau ) = 1] \}$
. We can regard A as an instance of
![]() $\mathsf {sTC}_{\mathbb {N}}$
, uniformly computable from f. Then
$\mathsf {sTC}_{\mathbb {N}}$
, uniformly computable from f. Then
![]() $A \neq \emptyset $
if and only if
$A \neq \emptyset $
if and only if
![]() $\{ \tau : f(\tau ) = 0 \}$
is not dense. Given
$\{ \tau : f(\tau ) = 0 \}$
is not dense. Given
![]() $-1$
as an
$-1$
as an
![]() $\mathsf {sTC}_{\mathbb {N}}$
-solution to A, we can then take
$\mathsf {sTC}_{\mathbb {N}}$
-solution to A, we can then take
![]() $\langle 0, \langle \rangle \rangle $
as a
$\langle 0, \langle \rangle \rangle $
as a
![]() $\mathsf {V}_{4}$
-solution to f. And given some
$\mathsf {V}_{4}$
-solution to f. And given some
![]() $\mathsf {sTC}_{\mathbb {N}}$
-solution to A different from
$\mathsf {sTC}_{\mathbb {N}}$
-solution to A different from
![]() $-1$
, coding a string
$-1$
, coding a string
![]() $\sigma \in 2^{<\omega }$
, we can take
$\sigma \in 2^{<\omega }$
, we can take
![]() $\langle 1,\sigma \rangle $
as a
$\langle 1,\sigma \rangle $
as a
![]() $\mathsf {V}_{4}$
-solution to f.
$\mathsf {V}_{4}$
-solution to f.
Now, to show that
![]() $\mathsf {sTC}_{\mathbb {N}} \leq _{\mathrm {W}} \mathsf {V}_{2}$
, fix an instance A of
$\mathsf {sTC}_{\mathbb {N}} \leq _{\mathrm {W}} \mathsf {V}_{2}$
, fix an instance A of
![]() $\mathsf {sTC}_{\mathbb {N}}$
, specified by a co-enumeration
$\mathsf {sTC}_{\mathbb {N}}$
, specified by a co-enumeration
![]() $e : \omega \to \omega $
. Let
$e : \omega \to \omega $
. Let
![]() $\ell $
be the function defined in the proof of Proposition 3.6. Define
$\ell $
be the function defined in the proof of Proposition 3.6. Define
![]() $f : 2^{<\omega } \to 2$
as follows: for every s, let
$f : 2^{<\omega } \to 2$
as follows: for every s, let
![]() $f(0^s) = 0$
; for every s and every
$f(0^s) = 0$
; for every s and every
![]() $\sigma \succeq 0^s1$
, let
$\sigma \succeq 0^s1$
, let
 $$\begin{align*}f(\sigma) = \begin{cases} 0 & \text{if } (\exists t)[s \leq t < |\sigma| \wedge \ell(t) \neq \ell(t+1)],\\ 1 & \text{otherwise}. \end{cases} \end{align*}$$
$$\begin{align*}f(\sigma) = \begin{cases} 0 & \text{if } (\exists t)[s \leq t < |\sigma| \wedge \ell(t) \neq \ell(t+1)],\\ 1 & \text{otherwise}. \end{cases} \end{align*}$$
Note that
![]() $A \neq \emptyset $
if and only if
$A \neq \emptyset $
if and only if
![]() $\lim _s \ell (s)$
exists (and belongs to A), if and only if there is a
$\lim _s \ell (s)$
exists (and belongs to A), if and only if there is a
![]() $\sigma $
such that
$\sigma $
such that
![]() $f(\tau ) = 1$
for all
$f(\tau ) = 1$
for all
![]() $\tau \succeq \sigma $
. So suppose
$\tau \succeq \sigma $
. So suppose
![]() $\langle i,\sigma \rangle $
is a
$\langle i,\sigma \rangle $
is a
![]() $\mathsf {V}_{2}$
-solution to f. If
$\mathsf {V}_{2}$
-solution to f. If
![]() $i = 0$
, then
$i = 0$
, then
![]() $\{ \tau : f(\tau ) = 0 \}$
is dense, hence by the previous observation we must have
$\{ \tau : f(\tau ) = 0 \}$
is dense, hence by the previous observation we must have
![]() $A = \emptyset $
. If
$A = \emptyset $
. If
![]() $i = 1$
, then we claim that
$i = 1$
, then we claim that
![]() $\ell (|\sigma |) \in A$
. Suppose not, so that for some
$\ell (|\sigma |) \in A$
. Suppose not, so that for some
![]() $t \geq |\sigma |$
we have
$t \geq |\sigma |$
we have
![]() $\ell (t) \neq \ell (t+1)$
. Fix
$\ell (t) \neq \ell (t+1)$
. Fix
![]() $\sigma ' \succeq \sigma 1$
with
$\sigma ' \succeq \sigma 1$
with
![]() $|\sigma '|> t$
. Then
$|\sigma '|> t$
. Then
![]() $\sigma ' \succeq 0^s1$
for some
$\sigma ' \succeq 0^s1$
for some
![]() $s \leq t$
, hence
$s \leq t$
, hence
![]() $s \leq t < |\sigma '|$
. By definition of f, we have that
$s \leq t < |\sigma '|$
. By definition of f, we have that
![]() $f(\tau ) = 0$
for all
$f(\tau ) = 0$
for all
![]() $\tau \succeq \sigma '$
. But since
$\tau \succeq \sigma '$
. But since
![]() $\langle 1,\sigma \rangle $
is a
$\langle 1,\sigma \rangle $
is a
![]() $\mathsf {V}_{2}$
-solution to f, we also have that
$\mathsf {V}_{2}$
-solution to f, we also have that
![]() $\{ \tau : f(\tau ) = 1 \}$
is dense above
$\{ \tau : f(\tau ) = 1 \}$
is dense above
![]() $\sigma $
, a contradiction. Thus, from any
$\sigma $
, a contradiction. Thus, from any
![]() $\mathsf {V}_{2}$
-solution to f we can uniformly computably determine whether or not A is empty, and if it not, determine an element of A, which completes the proof.
$\mathsf {V}_{2}$
-solution to f we can uniformly computably determine whether or not A is empty, and if it not, determine an element of A, which completes the proof.
We are now ready to prove the main theorem of this section.
Proof of Theorem 3.4.
We have only to justify that
![]() $\mathsf {V}_{0} \nleq _{\mathrm {W}} \mathsf {TT}^1_2$
and that
$\mathsf {V}_{0} \nleq _{\mathrm {W}} \mathsf {TT}^1_2$
and that
![]() $\mathsf {V}_{2} \nleq _{\mathrm {W}} \mathsf {V}_{1}$
. The former is a direct consequence of Corollary 5.9, to be proved later, which establishes the stronger fact that
$\mathsf {V}_{2} \nleq _{\mathrm {W}} \mathsf {V}_{1}$
. The former is a direct consequence of Corollary 5.9, to be proved later, which establishes the stronger fact that
![]() $\mathsf {TT}^1_2$
is not Weihrauch equivalent to any first-order problem. The latter follows from Propositions 3.6 and 3.7, and the fact that
$\mathsf {TT}^1_2$
is not Weihrauch equivalent to any first-order problem. The latter follows from Propositions 3.6 and 3.7, and the fact that
![]() $\mathsf {sTC}_{\mathbb {N}} \nleq _{\mathrm {W}} \mathsf {TC}_{\mathbb {N}}$
. To justify this last fact, consider for example the problem
$\mathsf {sTC}_{\mathbb {N}} \nleq _{\mathrm {W}} \mathsf {TC}_{\mathbb {N}}$
. To justify this last fact, consider for example the problem
![]() $\mathsf {isFinite}$
, whose instances are characteristic functions of subsets of
$\mathsf {isFinite}$
, whose instances are characteristic functions of subsets of
![]() $\omega $
having, as their unique solution, either
$\omega $
having, as their unique solution, either
![]() $1$
or
$1$
or
![]() $0$
depending as this subset is finite or infinite. Clearly,
$0$
depending as this subset is finite or infinite. Clearly,
![]() $\mathsf {isFinite} \leq _{\mathrm {W}} \mathsf {sTC}_{\mathbb {N}}$
since the set of upper bounds of a given subset of
$\mathsf {isFinite} \leq _{\mathrm {W}} \mathsf {sTC}_{\mathbb {N}}$
since the set of upper bounds of a given subset of
![]() $\omega $
is
$\omega $
is
![]() $\mathbf {\Pi }^0_1$
. But
$\mathbf {\Pi }^0_1$
. But
![]() $\mathsf {isFinite} \nleq _{\mathrm {W}} \mathsf {TC}_{\mathbb {N}}$
by a result of Neumann and Pauly [Reference Neumann and Pauly21, Proposition 24].
$\mathsf {isFinite} \nleq _{\mathrm {W}} \mathsf {TC}_{\mathbb {N}}$
by a result of Neumann and Pauly [Reference Neumann and Pauly21, Proposition 24].
4 Bounded number of colors
In this section, we analyze the strength of
![]() $\mathsf {TT}^1_k$
for fixed
$\mathsf {TT}^1_k$
for fixed
![]() $k \in \omega $
, as well as of
$k \in \omega $
, as well as of
![]() $\mathsf {TT}^1_+$
, which is
$\mathsf {TT}^1_+$
, which is
![]() $\mathsf {TT}^1$
restricted to colorings for which an upper bound on the number of colors is known explicitly.
$\mathsf {TT}^1$
restricted to colorings for which an upper bound on the number of colors is known explicitly.
As noted in Sections 1 and 2,
![]() $\mathsf {RT}^1_k \leq _{\mathrm {W}} \mathsf {TT}^1_k$
. It turns out that this is strict, in a strong sense that we now explain. First, we can show that
$\mathsf {RT}^1_k \leq _{\mathrm {W}} \mathsf {TT}^1_k$
. It turns out that this is strict, in a strong sense that we now explain. First, we can show that
![]() $\mathsf {RT}^1_k$
cannot be obtained from
$\mathsf {RT}^1_k$
cannot be obtained from
![]() $\mathsf {TT}^1$
using fewer than k many colors. This strengthens the result that
$\mathsf {TT}^1$
using fewer than k many colors. This strengthens the result that
![]() $\mathsf {RT}^1_k \nleq _{\mathrm {W}} \mathsf {RT}^1_j$
if
$\mathsf {RT}^1_k \nleq _{\mathrm {W}} \mathsf {RT}^1_j$
if
![]() $k> j$
, due independently to Brattka and Rakotoniaina [Reference Brattka and Rakotoniaina2, Theorem 4.22], Dorais, et al. [Reference Dorais, Dzhafarov, Hirst, Mileti and Shafer9, Theorem 3.1], and Hirschfeldt and Jockusch [Reference Hirschfeldt and Jockusch17, Theorem 3.4]. We thank the anonymous referee for pointing out that this result also follows from our Theorem 4.8 below and the fact that
$k> j$
, due independently to Brattka and Rakotoniaina [Reference Brattka and Rakotoniaina2, Theorem 4.22], Dorais, et al. [Reference Dorais, Dzhafarov, Hirst, Mileti and Shafer9, Theorem 3.1], and Hirschfeldt and Jockusch [Reference Hirschfeldt and Jockusch17, Theorem 3.4]. We thank the anonymous referee for pointing out that this result also follows from our Theorem 4.8 below and the fact that
![]() $\mathsf {RT}^1_k \nleq _{\mathrm {W}} \mathsf {D}^2_j$
for all
$\mathsf {RT}^1_k \nleq _{\mathrm {W}} \mathsf {D}^2_j$
for all
![]() $k> j$
(see [Reference Hirschfeldt and Jockusch17], Theorem 2.10). We include a direct proof here for completeness.
$k> j$
(see [Reference Hirschfeldt and Jockusch17], Theorem 2.10). We include a direct proof here for completeness.
Theorem 4.1. For every
![]() $k> j$
,
$k> j$
,
![]() $\mathsf {RT}^1_k \nleq _{\mathrm {W}} \mathsf {TT}^1_j$
.
$\mathsf {RT}^1_k \nleq _{\mathrm {W}} \mathsf {TT}^1_j$
.
Proof. The proof is quite similar to the proof that
![]() $\mathsf {RT}^1_k \nleq _{\mathrm {W}} \mathsf {RT}^1_j$
. We spell out the details. Suppose
$\mathsf {RT}^1_k \nleq _{\mathrm {W}} \mathsf {RT}^1_j$
. We spell out the details. Suppose
![]() $\mathsf {RT}^1_k \leq _{\mathrm {W}} \mathsf {TT}^1_j$
via
$\mathsf {RT}^1_k \leq _{\mathrm {W}} \mathsf {TT}^1_j$
via
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
. We define a sequence
$\Psi $
. We define a sequence
![]() $\alpha _0 \preceq \cdots \preceq \alpha _j$
of elements of
$\alpha _0 \preceq \cdots \preceq \alpha _j$
of elements of
![]() $k^{<\omega }$
, regarded as initial segments of an instance of
$k^{<\omega }$
, regarded as initial segments of an instance of
![]() $\mathsf {RT}^1_k$
, along with a sequence of strings
$\mathsf {RT}^1_k$
, along with a sequence of strings
![]() $\sigma _0 \preceq \cdots \preceq \sigma _j$
of
$\sigma _0 \preceq \cdots \preceq \sigma _j$
of
![]() $2^{<\omega }$
.
$2^{<\omega }$
.
Let
![]() $\alpha _0 = \langle \rangle $
and
$\alpha _0 = \langle \rangle $
and
![]() $\sigma _0 = \langle \rangle $
. Now fix
$\sigma _0 = \langle \rangle $
. Now fix
![]() $c < j$
and suppose
$c < j$
and suppose
![]() $\alpha _c$
and
$\alpha _c$
and
![]() $\sigma _c$
have been defined. Search for numbers
$\sigma _c$
have been defined. Search for numbers
![]() $m,n \in \omega $
and a finite set S satisfying the following:
$m,n \in \omega $
and a finite set S satisfying the following:
-
•
 $S \cong 2^{< n}$
, and the root of S extends
$S \cong 2^{< n}$
, and the root of S extends
 $\sigma _c$
;
$\sigma _c$
; -
•
 $\Phi (\alpha _c c^m)(\sigma ) \downarrow $
for all
$\Phi (\alpha _c c^m)(\sigma ) \downarrow $
for all
 $\sigma \in S$
and has the same value;
$\sigma \in S$
and has the same value; -
•
 $\Psi (\alpha _c c^m,S)(x) \downarrow = 1$
for some
$\Psi (\alpha _c c^m,S)(x) \downarrow = 1$
for some
 $x \geq |\alpha _c|$
.
$x \geq |\alpha _c|$
.
The search must succeed, because
![]() $g = \alpha _c c^\omega $
is an instance of
$g = \alpha _c c^\omega $
is an instance of
![]() $\mathsf {RT}^1_k$
, so
$\mathsf {RT}^1_k$
, so
![]() $\Phi (g)$
is in turn an instance f of
$\Phi (g)$
is in turn an instance f of
![]() $\mathsf {TT}^1_j$
. Moreover, for any
$\mathsf {TT}^1_j$
. Moreover, for any
![]() $H \cong 2^{<\omega }$
monochromatic for f with root extending
$H \cong 2^{<\omega }$
monochromatic for f with root extending
![]() $\sigma _c$
we must have that
$\sigma _c$
we must have that
![]() $\Psi (g,H)$
is an infinite monochromatic set for g. In this case, any sufficiently large initial segment of g can serve as
$\Psi (g,H)$
is an infinite monochromatic set for g. In this case, any sufficiently large initial segment of g can serve as
![]() $\alpha _c c^m$
, and any sufficiently large initial segment of H can serve as S.
$\alpha _c c^m$
, and any sufficiently large initial segment of H can serve as S.
Having found m and n, set
![]() $\alpha ^{\prime }_{c} = \alpha _c c^m$
. Without loss of generality, we may assume
$\alpha ^{\prime }_{c} = \alpha _c c^m$
. Without loss of generality, we may assume
![]() $m+|\alpha _c|> x$
for the x witnessing the third property above, so
$m+|\alpha _c|> x$
for the x witnessing the third property above, so
![]() $\alpha ^{\prime }_{c}(x)$
is defined and equal to c. Now, call
$\alpha ^{\prime }_{c}(x)$
is defined and equal to c. Now, call
![]() $\alpha \in k^{<\omega }$
c-good if
$\alpha \in k^{<\omega }$
c-good if
![]() $\alpha \succeq \alpha _c^{\prime }$
and
$\alpha \succeq \alpha _c^{\prime }$
and
![]() $\alpha (x)> c$
for all
$\alpha (x)> c$
for all
![]() $x \geq |\alpha _c^{\prime }|$
. Since
$x \geq |\alpha _c^{\prime }|$
. Since
![]() $c < j < k$
, c-good strings exist. Similarly, call
$c < j < k$
, c-good strings exist. Similarly, call
![]() $g : \omega \to k$
c-good if
$g : \omega \to k$
c-good if
![]() $g \succ \alpha _c^{\prime }$
and
$g \succ \alpha _c^{\prime }$
and
![]() $g(x)> c$
for all
$g(x)> c$
for all
![]() $x \geq |\alpha _c^{\prime }|$
. If g is c-good, then
$x \geq |\alpha _c^{\prime }|$
. If g is c-good, then
![]() $\Phi (g)(\sigma ) \downarrow $
for all
$\Phi (g)(\sigma ) \downarrow $
for all
![]() $\sigma \in S$
and has the same value, and
$\sigma \in S$
and has the same value, and
![]() $\Psi (g,S)(x) \downarrow = 1$
for some x with
$\Psi (g,S)(x) \downarrow = 1$
for some x with
![]() $g(x) = c$
. But g, being c-good, has no infinite monochromatic set of color c, so S cannot be extended to any
$g(x) = c$
. But g, being c-good, has no infinite monochromatic set of color c, so S cannot be extended to any
![]() $H \cong 2^{<\omega }$
monochromatic for
$H \cong 2^{<\omega }$
monochromatic for
![]() $\Phi (g)$
. In particular, it cannot be that for every leaf
$\Phi (g)$
. In particular, it cannot be that for every leaf
![]() $\lambda $
of S the set
$\lambda $
of S the set
![]() $\{ \sigma : \Phi (g)(\sigma ) = \Phi (g)(\lambda ) \}$
is dense above
$\{ \sigma : \Phi (g)(\sigma ) = \Phi (g)(\lambda ) \}$
is dense above
![]() $\lambda $
. It follows that there exists a c-good
$\lambda $
. It follows that there exists a c-good
![]() $\alpha $
, a leaf
$\alpha $
, a leaf
![]() $\lambda $
of S, and a string
$\lambda $
of S, and a string
![]() $\sigma \succeq \lambda $
such that for all c-good
$\sigma \succeq \lambda $
such that for all c-good
![]() $\beta \succeq \alpha $
and all
$\beta \succeq \alpha $
and all
![]() $\tau \succeq \sigma $
, if
$\tau \succeq \sigma $
, if
![]() $\Phi (\beta )(\tau ) \downarrow $
then
$\Phi (\beta )(\tau ) \downarrow $
then
![]() $\Phi (\beta )(\tau ) \neq \Phi (\beta )(\lambda )$
. Fix some such
$\Phi (\beta )(\tau ) \neq \Phi (\beta )(\lambda )$
. Fix some such
![]() $\alpha $
and
$\alpha $
and
![]() $\sigma $
, and let
$\sigma $
, and let
![]() $\alpha _{c+1} = \alpha $
and
$\alpha _{c+1} = \alpha $
and
![]() $\sigma _{c+1} = \sigma $
.
$\sigma _{c+1} = \sigma $
.
Now, fix any
![]() $g : \omega \to k$
extending
$g : \omega \to k$
extending
![]() $\alpha _j$
which is c-good for all
$\alpha _j$
which is c-good for all
![]() $c < j$
. Let
$c < j$
. Let
![]() $f = \Phi (g)$
. By assumption, f is a j-coloring. But by induction,
$f = \Phi (g)$
. By assumption, f is a j-coloring. But by induction,
![]() $|\{ f(\tau ) : \tau \succeq \sigma _c \}| \leq j-c$
for all
$|\{ f(\tau ) : \tau \succeq \sigma _c \}| \leq j-c$
for all
![]() $c \leq j$
. In particular, this means
$c \leq j$
. In particular, this means
![]() $|\{ f(\tau ) : \tau \succeq \sigma _j \}| = 0$
, which is impossible.
$|\{ f(\tau ) : \tau \succeq \sigma _j \}| = 0$
, which is impossible.
Since, as noted in the introduction,
![]() $\mathsf {RT}^1_k \leq _{\mathrm {W}} {}^1 \mathsf {TT}^1_k \leq _{\mathrm {W}} \mathsf {TT}^1_k$
for all k, we immediately get the following corollary.
$\mathsf {RT}^1_k \leq _{\mathrm {W}} {}^1 \mathsf {TT}^1_k \leq _{\mathrm {W}} \mathsf {TT}^1_k$
for all k, we immediately get the following corollary.
Corollary 4.2. For all
![]() $k> j$
,
$k> j$
,
![]() $\mathsf {TT}^1_k \nleq _{\mathrm {W}} \mathsf {TT}^1_j$
and
$\mathsf {TT}^1_k \nleq _{\mathrm {W}} \mathsf {TT}^1_j$
and
![]() ${}^1 \mathsf {TT}^1_k \nleq _{\mathrm {W}} {}^1 \mathsf {TT}^1_j$
.
${}^1 \mathsf {TT}^1_k \nleq _{\mathrm {W}} {}^1 \mathsf {TT}^1_j$
.
In the opposite direction, the next result shows that
![]() $\mathsf {TT}^1_k$
cannot be obtained from
$\mathsf {TT}^1_k$
cannot be obtained from
![]() $\mathsf {RT}^1$
no matter how many colors the latter is allowed to use. The proof is considerably more subtle and will serve as a basis for the remaining major theorems of this section. We first prove a lemma.
$\mathsf {RT}^1$
no matter how many colors the latter is allowed to use. The proof is considerably more subtle and will serve as a basis for the remaining major theorems of this section. We first prove a lemma.
Lemma 4.3. Fix
![]() $n \geq 1$
. Let
$n \geq 1$
. Let
![]() $S_i \subseteq 2^{< \omega }$
,
$S_i \subseteq 2^{< \omega }$
,
![]() $i < n$
, be pairwise disjoint sets of incomparable strings with
$i < n$
, be pairwise disjoint sets of incomparable strings with
![]() $|S_i| \geq n$
. There is a set of incomparable strings
$|S_i| \geq n$
. There is a set of incomparable strings
![]() $\{ \sigma _i : i < n \}$
such that
$\{ \sigma _i : i < n \}$
such that
![]() $\sigma _i \in S_i$
for each
$\sigma _i \in S_i$
for each
![]() $i < n$
.
$i < n$
.
Proof. The proof is by induction on n. For
![]() $n=1$
, the result is trivial, so assume
$n=1$
, the result is trivial, so assume
![]() $n> 1$
. Let
$n> 1$
. Let
![]() $S = \cup _{i < n} S_i$
. Fix
$S = \cup _{i < n} S_i$
. Fix
![]() $\sigma \in S$
such that
$\sigma \in S$
such that
![]() $\text {rk}_S(\sigma )$
is maximal. By reindexing the
$\text {rk}_S(\sigma )$
is maximal. By reindexing the
![]() $S_i$
sets if necessary, we can assume that
$S_i$
sets if necessary, we can assume that
![]() $\sigma \in S_{n-1}$
. Let
$\sigma \in S_{n-1}$
. Let
Because
![]() $\text {rk}_S(\sigma )$
is maximal, there are no strings
$\text {rk}_S(\sigma )$
is maximal, there are no strings
![]() $\tau \in S$
such that
$\tau \in S$
such that
![]() $\sigma \prec \tau $
. Since the sets
$\sigma \prec \tau $
. Since the sets
![]() $S_i$
consist of incomparable strings, it follows that
$S_i$
consist of incomparable strings, it follows that
![]() $|S_i \setminus S_i^{\prime }| \leq 1$
, and hence
$|S_i \setminus S_i^{\prime }| \leq 1$
, and hence
![]() $|S_i^{\prime }| \geq n-1$
, for each
$|S_i^{\prime }| \geq n-1$
, for each
![]() $i < n-1$
. Therefore, we can apply the inductive hypothesis to choose a set of incomparable strings
$i < n-1$
. Therefore, we can apply the inductive hypothesis to choose a set of incomparable strings
![]() $\sigma _i \in S^{\prime }_i$
for
$\sigma _i \in S^{\prime }_i$
for
![]() $i < n-1$
. The set
$i < n-1$
. The set
![]() $\{ \sigma _0, \ldots , \sigma _{n-2}, \sigma \}$
is the desired set of incomparable strings.
$\{ \sigma _0, \ldots , \sigma _{n-2}, \sigma \}$
is the desired set of incomparable strings.
The following result may be regarded as an analog of Lemma 3.8 of Corduan, Groszek, and Mileti [Reference Corduan, Groszek and Mileti6], which establishes that
![]() $\mathsf {RCA}_0 + \mathsf {B}\Sigma ^0_2$
does not prove
$\mathsf {RCA}_0 + \mathsf {B}\Sigma ^0_2$
does not prove
![]() $\mathsf {TT}^1$
.
$\mathsf {TT}^1$
.
Theorem 4.4. For every
![]() $k \geq 2$
and every
$k \geq 2$
and every
![]() $j \geq 1$
,
$j \geq 1$
,
![]() ${}^1 \mathsf {TT}^1_k \nleq _{\mathrm {W}} \mathsf {RT}^1_j$
.
${}^1 \mathsf {TT}^1_k \nleq _{\mathrm {W}} \mathsf {RT}^1_j$
.
Proof. It suffices to prove the result for
![]() $k = 2$
. Seeking a contradiction, suppose
$k = 2$
. Seeking a contradiction, suppose
![]() ${}^1 \mathsf {TT}^1_2 \leq _{\mathrm {W}} \mathsf {RT}^1_j$
via
${}^1 \mathsf {TT}^1_2 \leq _{\mathrm {W}} \mathsf {RT}^1_j$
via
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
. Let
$\Psi $
. Let
![]() $\Gamma $
be a functional such that, given
$\Gamma $
be a functional such that, given
![]() $f : 2^{<\omega } \to 2$
and
$f : 2^{<\omega } \to 2$
and
![]() $S \cong 2^{<\omega }$
,
$S \cong 2^{<\omega }$
,
![]() $\Gamma (f,S)(0)$
outputs
$\Gamma (f,S)(0)$
outputs
![]() $\langle \sigma _0,\ldots ,\sigma _{j-1} \rangle $
for the least j many pairwise incomparable strings
$\langle \sigma _0,\ldots ,\sigma _{j-1} \rangle $
for the least j many pairwise incomparable strings
![]() $\sigma _0,\ldots ,\sigma _{j-1} \in S$
. In particular, for every
$\sigma _0,\ldots ,\sigma _{j-1} \in S$
. In particular, for every
![]() $f : 2^{<\omega } \to 2$
,
$f : 2^{<\omega } \to 2$
,
![]() $\langle f,\mathrm {Id},\Gamma \rangle $
is an instance of
$\langle f,\mathrm {Id},\Gamma \rangle $
is an instance of
![]() ${}^1 \mathsf {TT}^1_2$
. Hence by assumption,
${}^1 \mathsf {TT}^1_2$
. Hence by assumption,
![]() $\Phi (f,\mathrm {Id},\Gamma )$
is an instance g of
$\Phi (f,\mathrm {Id},\Gamma )$
is an instance g of
![]() $\mathsf {RT}^1_j$
. Moreover, note that for each
$\mathsf {RT}^1_j$
. Moreover, note that for each
![]() $c < j$
, either
$c < j$
, either
![]() $g(x) \neq c$
for all sufficiently large x, or there is a finite set E monochromatic for g with color c such that
$g(x) \neq c$
for all sufficiently large x, or there is a finite set E monochromatic for g with color c such that
![]() $\Psi (f,\mathrm {Id},\Gamma ,E)(0) \downarrow = \langle \sigma _0,\ldots ,\sigma _{j-1} \rangle $
for some pairwise incomparable strings
$\Psi (f,\mathrm {Id},\Gamma ,E)(0) \downarrow = \langle \sigma _0,\ldots ,\sigma _{j-1} \rangle $
for some pairwise incomparable strings
![]() $\sigma _0,\ldots ,\sigma _{j-1}$
.
$\sigma _0,\ldots ,\sigma _{j-1}$
.
Consider Cohen forcing, with conditions
![]() $\alpha \in 2^{<\omega }$
regarded as initial segments of a
$\alpha \in 2^{<\omega }$
regarded as initial segments of a
![]() $2$
-coloring of
$2$
-coloring of
![]() $2^{<\omega }$
. Let
$2^{<\omega }$
. Let
![]() $\check {f}$
be a name in the forcing language for a generic such
$\check {f}$
be a name in the forcing language for a generic such
![]() $2$
-coloring, and let
$2$
-coloring, and let
![]() $\check {g}$
be a name for
$\check {g}$
be a name for
![]() $\Phi (\check {f},\mathrm {Id},\Gamma )$
. From the above discussion, it follows that we can find a condition
$\Phi (\check {f},\mathrm {Id},\Gamma )$
. From the above discussion, it follows that we can find a condition
![]() $\alpha $
along with a number
$\alpha $
along with a number
![]() $n_0$
, a non-empty set
$n_0$
, a non-empty set
![]() $C \subseteq j$
and, for each
$C \subseteq j$
and, for each
![]() $c \in C$
, a finite set
$c \in C$
, a finite set
![]() $E_c$
, such that
$E_c$
, such that
![]() $\alpha $
forces each of the following:
$\alpha $
forces each of the following:
-
•
 $E_c$
is monochromatic for
$E_c$
is monochromatic for
 $\check {g}$
with color c;
$\check {g}$
with color c; -
•
 $\Psi (\check {f},\mathrm {Id},\Gamma ,E_c)(0) \downarrow $
;
$\Psi (\check {f},\mathrm {Id},\Gamma ,E_c)(0) \downarrow $
; -
•
 $\check {g}(x) \in C$
for all
$\check {g}(x) \in C$
for all
 $x> n_0$
.
$x> n_0$
.
Notice that the first two clauses are
![]() $\Sigma ^0_1$
, while the third is
$\Sigma ^0_1$
, while the third is
![]() $\Pi ^0_1$
. Therefore, if
$\Pi ^0_1$
. Therefore, if
![]() $f : 2^{<\omega } \to 2$
is any coloring extending
$f : 2^{<\omega } \to 2$
is any coloring extending
![]() $\alpha $
, whether generic or not, each of the above clauses holds if
$\alpha $
, whether generic or not, each of the above clauses holds if
![]() $\check {f}$
is replaced by f and
$\check {f}$
is replaced by f and
![]() $\check {g}$
by
$\check {g}$
by
![]() $g = \Phi (f,\mathrm {Id},\Gamma )$
.
$g = \Phi (f,\mathrm {Id},\Gamma )$
.
By definition of
![]() $\Gamma $
, for each
$\Gamma $
, for each
![]() $c \in C$
we have
$c \in C$
we have
![]() $\Psi (\alpha ,\mathrm {Id},\Gamma ,E_c)(0) = \langle \sigma _{c,0},\ldots ,\sigma _{c,j-1} \rangle $
for some pairwise incomparable strings
$\Psi (\alpha ,\mathrm {Id},\Gamma ,E_c)(0) = \langle \sigma _{c,0},\ldots ,\sigma _{c,j-1} \rangle $
for some pairwise incomparable strings
![]() $\sigma _{c,0},\ldots ,\sigma _{c,j-1} \in 2^{<\omega }$
. By standard use conventions, we may assume
$\sigma _{c,0},\ldots ,\sigma _{c,j-1} \in 2^{<\omega }$
. By standard use conventions, we may assume
![]() $\sigma _{c,0},\ldots ,\sigma _{c,j-1} < |\alpha |$
for all c. Apply Lemma 4.3 to choose
$\sigma _{c,0},\ldots ,\sigma _{c,j-1} < |\alpha |$
for all c. Apply Lemma 4.3 to choose
![]() $\sigma _c \in \{ \sigma _{c,0},\ldots ,\sigma _{c,j-1} \}$
for each
$\sigma _c \in \{ \sigma _{c,0},\ldots ,\sigma _{c,j-1} \}$
for each
![]() $c \in C$
such that
$c \in C$
such that
![]() $\{ \sigma _c : c \in C \}$
is a set of incomparable strings.
$\{ \sigma _c : c \in C \}$
is a set of incomparable strings.
Finally, we are ready to define f. For all
![]() $\sigma < |\alpha |$
, let
$\sigma < |\alpha |$
, let
![]() $f(\sigma ) = \alpha (\sigma )$
. As noted above, this defines
$f(\sigma ) = \alpha (\sigma )$
. As noted above, this defines
![]() $f(\sigma _c) = \alpha (\sigma _c)$
for all
$f(\sigma _c) = \alpha (\sigma _c)$
for all
![]() $c \in C$
. If
$c \in C$
. If
![]() $\sigma \geq |\alpha |$
and
$\sigma \geq |\alpha |$
and
![]() $\sigma \nsucceq \sigma _c$
for all
$\sigma \nsucceq \sigma _c$
for all
![]() $c \in C$
, let
$c \in C$
, let
![]() $f(\sigma ) = 0$
. If
$f(\sigma ) = 0$
. If
![]() $\sigma \geq |\alpha |$
and
$\sigma \geq |\alpha |$
and
![]() $\sigma \succeq \sigma _c$
for some
$\sigma \succeq \sigma _c$
for some
![]() $c \in C$
, then
$c \in C$
, then
![]() $\sigma \nsucceq \sigma _d$
for all
$\sigma \nsucceq \sigma _d$
for all
![]() $d \neq c$
in C since
$d \neq c$
in C since
![]() $\sigma _d$
and
$\sigma _d$
and
![]() $\sigma _c$
are incomparable. In this case, we let
$\sigma _c$
are incomparable. In this case, we let
![]() $f(\sigma ) = 1 - f(\sigma _c)$
. This completes the definition. To complete the proof, let
$f(\sigma ) = 1 - f(\sigma _c)$
. This completes the definition. To complete the proof, let
![]() $g = \Phi (f,\mathrm {Id},\Gamma )$
. Since f extends
$g = \Phi (f,\mathrm {Id},\Gamma )$
. Since f extends
![]() $\alpha $
it follows by our earlier remark that each
$\alpha $
it follows by our earlier remark that each
![]() $E_c$
is monochromatic for g with color c, and every infinite monochromatic set for g has color some
$E_c$
is monochromatic for g with color c, and every infinite monochromatic set for g has color some
![]() $c \in C$
. It follows that for some
$c \in C$
. It follows that for some
![]() $c \in C$
,
$c \in C$
,
![]() $E_c$
is extendible to an
$E_c$
is extendible to an
![]() $\mathsf {RT}^1_j$
-solution to g, and therefore
$\mathsf {RT}^1_j$
-solution to g, and therefore
![]() $\langle \sigma _{c,0},\ldots ,\sigma _{c,j-1} \rangle $
is a
$\langle \sigma _{c,0},\ldots ,\sigma _{c,j-1} \rangle $
is a
![]() ${}^1 \mathsf {TT}^1_2$
-solution to
${}^1 \mathsf {TT}^1_2$
-solution to
![]() $\langle f,\mathrm {Id},\Gamma \rangle $
. This means that
$\langle f,\mathrm {Id},\Gamma \rangle $
. This means that
![]() $\langle \sigma _{c,0},\ldots ,\sigma _{c,j-1} \rangle = \Gamma (f,H)$
for some
$\langle \sigma _{c,0},\ldots ,\sigma _{c,j-1} \rangle = \Gamma (f,H)$
for some
![]() $H \cong 2^{<\omega }$
monochromatic for f. But for every
$H \cong 2^{<\omega }$
monochromatic for f. But for every
![]() $\sigma \succeq \sigma _c$
with
$\sigma \succeq \sigma _c$
with
![]() $|\sigma | \geq \alpha $
, and in particular, for every such
$|\sigma | \geq \alpha $
, and in particular, for every such
![]() $\sigma \in H$
, we have that
$\sigma \in H$
, we have that
![]() $f(\sigma ) \neq f(\sigma _c)$
. Thus, H cannot be monochromatic for f, a contradiction.
$f(\sigma ) \neq f(\sigma _c)$
. Thus, H cannot be monochromatic for f, a contradiction.
Corollary 4.5. For every
![]() $k \geq 2$
and every
$k \geq 2$
and every
![]() $j \geq 1$
,
$j \geq 1$
,
![]() $\mathsf {TT}^1_k \nleq _{\mathrm {W}} \mathsf {RT}^1_j$
.
$\mathsf {TT}^1_k \nleq _{\mathrm {W}} \mathsf {RT}^1_j$
.
At first blush, it may seem that
![]() $\mathsf {RT}^1_j$
in the statement of Theorem 4.4 could be replaced by
$\mathsf {RT}^1_j$
in the statement of Theorem 4.4 could be replaced by
![]() $\mathsf {RT}^1_+$
. After all, an instance of
$\mathsf {RT}^1_+$
. After all, an instance of
![]() $\mathsf {RT}^1_+$
is an instance of
$\mathsf {RT}^1_+$
is an instance of
![]() $\mathsf {RT}^1_j$
for some j, and this j is specified. But there is a problem with lifting the proof directly. Namely, the instance of
$\mathsf {RT}^1_j$
for some j, and this j is specified. But there is a problem with lifting the proof directly. Namely, the instance of
![]() ${}^1 \mathsf {TT}^1_k$
constructed in the proof requires both an instance f of
${}^1 \mathsf {TT}^1_k$
constructed in the proof requires both an instance f of
![]() $\mathsf {TT}^1_k$
and a functional
$\mathsf {TT}^1_k$
and a functional
![]() $\Gamma $
, and this functional very much depends on j. The number j is, in turn, computed via a hypothetical reduction
$\Gamma $
, and this functional very much depends on j. The number j is, in turn, computed via a hypothetical reduction
![]() $\Phi $
from both f and
$\Phi $
from both f and
![]() $\Gamma $
, which results in a circularity. The natural attempt to get around this is to use the recursion theorem, and this works, but at a cost: the argument only works to show that
$\Gamma $
, which results in a circularity. The natural attempt to get around this is to use the recursion theorem, and this works, but at a cost: the argument only works to show that
![]() ${}^1 \mathsf {TT}^1_k \nleq _{\mathrm {W}} \mathsf {RT}^1_+$
for
${}^1 \mathsf {TT}^1_k \nleq _{\mathrm {W}} \mathsf {RT}^1_+$
for
![]() $k \geq 3$
.
$k \geq 3$
.
Theorem 4.6. For every
![]() $k \geq 3$
,
$k \geq 3$
,
![]() ${}^1 \mathsf {TT}^1_k \nleq _{\mathrm {W}} \mathsf {RT}^1_+$
.
${}^1 \mathsf {TT}^1_k \nleq _{\mathrm {W}} \mathsf {RT}^1_+$
.
Proof. It suffices to prove the result for
![]() $k = 3$
. Suppose to the contrary that
$k = 3$
. Suppose to the contrary that
![]() ${}^1 \mathsf {TT}^1_3 \leq _{\mathrm {W}} \mathsf {RT}^1_+$
, say via
${}^1 \mathsf {TT}^1_3 \leq _{\mathrm {W}} \mathsf {RT}^1_+$
, say via
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
. We build a
$\Psi $
. We build a
![]() $3$
-coloring f of
$3$
-coloring f of
![]() $2^{<\omega }$
and a Turing functional
$2^{<\omega }$
and a Turing functional
![]() $\Gamma $
so that
$\Gamma $
so that
![]() $\langle f,\mathrm {Id},\Gamma \rangle $
is an instance of
$\langle f,\mathrm {Id},\Gamma \rangle $
is an instance of
![]() ${}^1 \mathsf {TT}^1_3$
witnessing a contradiction. The way we define
${}^1 \mathsf {TT}^1_3$
witnessing a contradiction. The way we define
![]() $\Gamma $
is as follows. Let
$\Gamma $
is as follows. Let
![]() $\Delta _0,\Delta _1,\ldots $
be the standard enumeration of all oracle Turing functionals (so named in order to avoid notationally clashing with the fixed functional
$\Delta _0,\Delta _1,\ldots $
be the standard enumeration of all oracle Turing functionals (so named in order to avoid notationally clashing with the fixed functional
![]() $\Phi $
). We define a certain computable function h and then choose a fixed point
$\Phi $
). We define a certain computable function h and then choose a fixed point
![]() $e_0$
for h using the recursion theorem, so that
$e_0$
for h using the recursion theorem, so that
![]() $\Delta _{h(e_0)}(A) = \Delta _{e_0}(A)$
for all oracles A. We then let
$\Delta _{h(e_0)}(A) = \Delta _{e_0}(A)$
for all oracles A. We then let
![]() $\Gamma = \Delta _{e_0}$
.
$\Gamma = \Delta _{e_0}$
.
For the definition of h, we decompose each oracle A as
![]() $\langle f,S \rangle $
, with our interest being in the situation where f is a
$\langle f,S \rangle $
, with our interest being in the situation where f is a
![]() $3$
-coloring of
$3$
-coloring of
![]() $2^{<\omega }$
and S is a monochromatic set for f. Of course, for an arbitrary A, either f or S or both may fail to have these properties, but we do not care about these cases. We obtain h using the s-m-n theorem so as to satisfy the following properties, for all
$2^{<\omega }$
and S is a monochromatic set for f. Of course, for an arbitrary A, either f or S or both may fail to have these properties, but we do not care about these cases. We obtain h using the s-m-n theorem so as to satisfy the following properties, for all
![]() $e \in \omega $
and all oracles
$e \in \omega $
and all oracles
![]() $A = \langle f,S \rangle $
. First, find the least
$A = \langle f,S \rangle $
. First, find the least
![]() $\sigma \in S$
. If
$\sigma \in S$
. If
![]() $f(\sigma ) = 0$
, then let
$f(\sigma ) = 0$
, then let
![]() $\Delta _{h(e)}(A)(0) \downarrow = \sigma $
. If
$\Delta _{h(e)}(A)(0) \downarrow = \sigma $
. If
![]() $f(\sigma )> 0$
, then wait for
$f(\sigma )> 0$
, then wait for
![]() $\Phi (f,\mathrm {Id},\Delta _e)(0)$
to converge and output a number
$\Phi (f,\mathrm {Id},\Delta _e)(0)$
to converge and output a number
![]() $j \geq 1$
. (The idea is that if
$j \geq 1$
. (The idea is that if
![]() $\langle f,\mathrm {Id},\Delta _e \rangle $
is an instance of
$\langle f,\mathrm {Id},\Delta _e \rangle $
is an instance of
![]() ${}^1 \mathsf {TT}^1_3$
, then
${}^1 \mathsf {TT}^1_3$
, then
![]() $\Phi (f,\mathrm {Id},\Delta _e)$
is an instance
$\Phi (f,\mathrm {Id},\Delta _e)$
is an instance
![]() $\langle j,g \rangle $
of
$\langle j,g \rangle $
of
![]() $\mathsf {RT}^1_+$
, so
$\mathsf {RT}^1_+$
, so
![]() $\Phi (f,\mathrm {Id},\Delta _e)(0) = j$
.) Then, find the first j many incomparable strings
$\Phi (f,\mathrm {Id},\Delta _e)(0) = j$
.) Then, find the first j many incomparable strings
![]() $\sigma _0,\ldots ,\sigma _{j-1} \in S$
and let
$\sigma _0,\ldots ,\sigma _{j-1} \in S$
and let
![]() $\Delta _{h(e)}(A)(0) \downarrow = \langle \sigma _0,\ldots ,\sigma _{j-1} \rangle $
.
$\Delta _{h(e)}(A)(0) \downarrow = \langle \sigma _0,\ldots ,\sigma _{j-1} \rangle $
.
Let
![]() $\Gamma $
be as described above, and consider the trivial coloring
$\Gamma $
be as described above, and consider the trivial coloring
![]() $f_0 : 2^{<\omega } \to 3$
such that
$f_0 : 2^{<\omega } \to 3$
such that
![]() $f_0(\sigma ) = 0$
for all
$f_0(\sigma ) = 0$
for all
![]() $\sigma \in 2^{<\omega }$
. If
$\sigma \in 2^{<\omega }$
. If
![]() $H \cong 2^{<\omega }$
is monochromatic for
$H \cong 2^{<\omega }$
is monochromatic for
![]() $f_0$
then it is clear from the definition that
$f_0$
then it is clear from the definition that
![]() $\Gamma (f_0,H)(0) \downarrow $
. (Namely,
$\Gamma (f_0,H)(0) \downarrow $
. (Namely,
![]() $\Gamma (f_0,H)(0)$
outputs the least string in H.) Thus,
$\Gamma (f_0,H)(0)$
outputs the least string in H.) Thus,
![]() $\langle f_0,\mathrm {Id},\Gamma \rangle $
is an instance of
$\langle f_0,\mathrm {Id},\Gamma \rangle $
is an instance of
![]() ${}^1 \mathsf {TT}^1_3$
. By assumption,
${}^1 \mathsf {TT}^1_3$
. By assumption,
![]() $\Phi (f_0,\mathrm {Id},\Gamma )(0) \downarrow = j$
for some
$\Phi (f_0,\mathrm {Id},\Gamma )(0) \downarrow = j$
for some
![]() $j \geq 1$
. Fix a finite initial segment
$j \geq 1$
. Fix a finite initial segment
![]() $\alpha _0 \prec f_0$
such that
$\alpha _0 \prec f_0$
such that
![]() $\Phi (\alpha _0,\mathrm {Id},\Gamma )(0) \downarrow = j$
. Say
$\Phi (\alpha _0,\mathrm {Id},\Gamma )(0) \downarrow = j$
. Say
![]() $f : 2^{<\omega } \to 3$
is good if f extends
$f : 2^{<\omega } \to 3$
is good if f extends
![]() $\alpha _0$
and
$\alpha _0$
and
![]() $f(\sigma ) \neq 0$
for all
$f(\sigma ) \neq 0$
for all
![]() $\sigma \geq |\alpha _0|$
. Similarly, say
$\sigma \geq |\alpha _0|$
. Similarly, say
![]() $\alpha \in 3^{<\omega }$
, regarded as a
$\alpha \in 3^{<\omega }$
, regarded as a
![]() $3$
-coloring of a finite subset of
$3$
-coloring of a finite subset of
![]() $2^{<\omega }$
, is good if
$2^{<\omega }$
, is good if
![]() $\alpha _0 \preceq \alpha $
and
$\alpha _0 \preceq \alpha $
and
![]() $\alpha (\sigma ) \neq 0$
for all
$\alpha (\sigma ) \neq 0$
for all
![]() $\sigma \geq |\alpha _0|$
.
$\sigma \geq |\alpha _0|$
.
Now, consider any good coloring
![]() $f : 2^{<\omega } \to 3$
. Then
$f : 2^{<\omega } \to 3$
. Then
![]() $\langle f,\mathrm {Id},\Gamma \rangle $
is an instance of
$\langle f,\mathrm {Id},\Gamma \rangle $
is an instance of
![]() ${}^1 \mathsf {TT}^1_3$
. Indeed, we have that
${}^1 \mathsf {TT}^1_3$
. Indeed, we have that
![]() $\Phi (f,\mathrm {Id},\Gamma )(0) \downarrow = j$
since f extends
$\Phi (f,\mathrm {Id},\Gamma )(0) \downarrow = j$
since f extends
![]() $\alpha _0$
. Moreover, any
$\alpha _0$
. Moreover, any
![]() $H \cong 2^{<\omega }$
monochromatic for f must have color
$H \cong 2^{<\omega }$
monochromatic for f must have color
![]() $1$
or
$1$
or
![]() $2$
. Thus, by definition of
$2$
. Thus, by definition of
![]() $\Gamma $
, we have that
$\Gamma $
, we have that
![]() $\Gamma (f,H)(0) \downarrow = \langle \sigma _0,\ldots ,\sigma _{j-1} \rangle $
for the least j many incomparable strings
$\Gamma (f,H)(0) \downarrow = \langle \sigma _0,\ldots ,\sigma _{j-1} \rangle $
for the least j many incomparable strings
![]() $\sigma _0,\ldots ,\sigma _{j-1} \in H$
. And
$\sigma _0,\ldots ,\sigma _{j-1} \in H$
. And
![]() $\Phi (f,\mathrm {Id},\Gamma ) = \langle j,g \rangle $
for some instance g of
$\Phi (f,\mathrm {Id},\Gamma ) = \langle j,g \rangle $
for some instance g of
![]() $\mathsf {RT}^1_j$
. So we can now proceed precisely as in the proof of Theorem 4.4, only working with good conditions in
$\mathsf {RT}^1_j$
. So we can now proceed precisely as in the proof of Theorem 4.4, only working with good conditions in
![]() $3^{<\omega }$
, and building a good
$3^{<\omega }$
, and building a good
![]() $3$
-coloring f.
$3$
-coloring f.
Remarkably, after a preprint of this paper was circulated, Pauly [Reference Pauly22] has shown that
![]() ${}^1 \mathsf {TT}^1_2 \leq _{\mathrm {W}} \mathsf {RT}^1_+$
. Thus, Theorem 4.6 is optimal.
${}^1 \mathsf {TT}^1_2 \leq _{\mathrm {W}} \mathsf {RT}^1_+$
. Thus, Theorem 4.6 is optimal.
We now move from
![]() ${}^1 \mathsf {TT}^1_k$
to
${}^1 \mathsf {TT}^1_k$
to
![]() $\mathsf {TT}^1_k$
, and from
$\mathsf {TT}^1_k$
, and from
![]() $\mathsf {RT}^1_+$
to
$\mathsf {RT}^1_+$
to
![]() $\mathsf {RT}^1_{\mathbb {N}}$
. The obstacle with needing to know a functional
$\mathsf {RT}^1_{\mathbb {N}}$
. The obstacle with needing to know a functional
![]() $\Gamma $
“in advance” does not arise here (since we do not need to build an instance of a first-order part), so we get a result that holds for all
$\Gamma $
“in advance” does not arise here (since we do not need to build an instance of a first-order part), so we get a result that holds for all
![]() $k \geq 2$
.
$k \geq 2$
.
Theorem 4.7. For every
![]() $k \geq 2$
,
$k \geq 2$
,
![]() $\mathsf {TT}^1_k \nleq _{\mathrm {W}} \mathsf {RT}^1_{\mathbb {N}}$
.
$\mathsf {TT}^1_k \nleq _{\mathrm {W}} \mathsf {RT}^1_{\mathbb {N}}$
.
Proof. Again, the proof is based on that of Theorem 4.4, but with some small differences. As there, we can take
![]() $k = 2$
, and then argue by contradiction. So, asume that
$k = 2$
, and then argue by contradiction. So, asume that
![]() $\mathsf {TT}^1_2 \leq _{\mathrm {W}} \mathsf {RT}^1_{\mathbb {N}}$
, via
$\mathsf {TT}^1_2 \leq _{\mathrm {W}} \mathsf {RT}^1_{\mathbb {N}}$
, via
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
. Consider Cohen forcing in
$\Psi $
. Consider Cohen forcing in
![]() $2^{<\omega }$
, let
$2^{<\omega }$
, let
![]() $\check {f}$
be as in Theorem 4.4, and let
$\check {f}$
be as in Theorem 4.4, and let
![]() $\check {g}$
be a name in the forcing language for
$\check {g}$
be a name in the forcing language for
![]() $\Phi (\check {f})$
. Since a generic here is an instance of
$\Phi (\check {f})$
. Since a generic here is an instance of
![]() $\mathsf {TT}^1_2$
, which is in turn mapped by
$\mathsf {TT}^1_2$
, which is in turn mapped by
![]() $\Phi $
to an instance of
$\Phi $
to an instance of
![]() $\mathsf {RT}^1_{\mathbb {N}}$
, it follows that we can fix a
$\mathsf {RT}^1_{\mathbb {N}}$
, it follows that we can fix a
![]() $j \geq 1$
and a condition
$j \geq 1$
and a condition
![]() $\alpha _0$
forcing that
$\alpha _0$
forcing that
![]() $\check {g}$
is a j-coloring. This can be expressed as a
$\check {g}$
is a j-coloring. This can be expressed as a
![]() $\Pi ^0_1$
property, hence it will be preserved by any
$\Pi ^0_1$
property, hence it will be preserved by any
![]() $2$
-coloring of
$2$
-coloring of
![]() $2^{<\omega }$
that extends
$2^{<\omega }$
that extends
![]() $\alpha _0$
, generic or not. We can now proceed basically just like in Theorem 4.4, but working below
$\alpha _0$
, generic or not. We can now proceed basically just like in Theorem 4.4, but working below
![]() $\alpha _0$
. More precisely, we find a condition
$\alpha _0$
. More precisely, we find a condition
![]() $\alpha \geq \alpha _0$
along with a number
$\alpha \geq \alpha _0$
along with a number
![]() $n_0$
, a non-empty set
$n_0$
, a non-empty set
![]() $C \subseteq j$
and, for each
$C \subseteq j$
and, for each
![]() $c \in C$
, a finite set
$c \in C$
, a finite set
![]() $E_c$
, such that
$E_c$
, such that
![]() $\alpha $
forces each of the following:
$\alpha $
forces each of the following:
-
•
 $E_c$
is monochromatic for
$E_c$
is monochromatic for
 $\check {g}$
with color c;
$\check {g}$
with color c; -
•
 $\Psi (\check {f},E_c)(\sigma ) \downarrow = 1$
for j many pairwise incomparable strings
$\Psi (\check {f},E_c)(\sigma ) \downarrow = 1$
for j many pairwise incomparable strings
 $\sigma $
;
$\sigma $
; -
•
 $\check {g}(x) \in C$
for all
$\check {g}(x) \in C$
for all
 $x> n_0$
.
$x> n_0$
.
The rest of the construction of a
![]() $2$
-coloring
$2$
-coloring
![]() $f \succeq \alpha $
of
$f \succeq \alpha $
of
![]() $2^{<\omega }$
is now just as before.
$2^{<\omega }$
is now just as before.
Theorems 4.6 and 4.7 raise two natural questions. The first is what happens between
![]() ${}^1 \mathsf {TT}^1_k$
and
${}^1 \mathsf {TT}^1_k$
and
![]() $\mathsf {RT}^1_{\mathbb {N}}$
, and the second is what happens between
$\mathsf {RT}^1_{\mathbb {N}}$
, and the second is what happens between
![]() ${}^1 \mathsf {TT}^1_k$
and
${}^1 \mathsf {TT}^1_k$
and
![]() $\mathsf {TT}^1_k$
. These questions will be answered in the next section, in Corollaries 5.8 and 5.9.
$\mathsf {TT}^1_k$
. These questions will be answered in the next section, in Corollaries 5.8 and 5.9.
We conclude by looking at the relationship of
![]() $\mathsf {TT}^1_k$
and
$\mathsf {TT}^1_k$
and
![]() $\mathsf {D}^2_k$
, a close relative of
$\mathsf {D}^2_k$
, a close relative of
![]() $\mathsf {RT}^1_k$
. Recall that
$\mathsf {RT}^1_k$
. Recall that
![]() $\mathsf {D}^2_k$
is the problem whose instances are all
$\mathsf {D}^2_k$
is the problem whose instances are all
![]() $\mathbf {\Delta }^0_2$
colorings
$\mathbf {\Delta }^0_2$
colorings
![]() $f : \omega \to k$
, with the solution to any such f being all infinite set
$f : \omega \to k$
, with the solution to any such f being all infinite set
![]() $M \subseteq \omega $
homogeneous for f. This problem, formulated as a statement of second-order arithmetic, was introduced by Cholak, Jockusch, and Slaman [Reference Cholak, Jockusch and Slaman3, Statement 7.8], and has played an important role in the reverse mathematical analysis of Ramsey’s theorem for pairs. (See [Reference Dzhafarov and Mummert12, Sections 8] for more of the history.)
$M \subseteq \omega $
homogeneous for f. This problem, formulated as a statement of second-order arithmetic, was introduced by Cholak, Jockusch, and Slaman [Reference Cholak, Jockusch and Slaman3, Statement 7.8], and has played an important role in the reverse mathematical analysis of Ramsey’s theorem for pairs. (See [Reference Dzhafarov and Mummert12, Sections 8] for more of the history.)
Often, the instances of
![]() $\mathsf {D}^2_k$
are represented using Schoenfield’s limit lemma, as colorings
$\mathsf {D}^2_k$
are represented using Schoenfield’s limit lemma, as colorings
![]() $f : \omega ^2 \to k$
with the property that
$f : \omega ^2 \to k$
with the property that
![]() $\lim _y f(x,y)$
exists for all x. Here, we think of them as pairs
$\lim _y f(x,y)$
exists for all x. Here, we think of them as pairs
![]() $(X,f)$
where X is an arbitrary set and f is an
$(X,f)$
where X is an arbitrary set and f is an
![]() $X'$
-computable instance of
$X'$
-computable instance of
![]() $\mathsf {RT}^1_k$
. In jargon,
$\mathsf {RT}^1_k$
. In jargon,
![]() $\mathsf {D}^2_k$
is
$\mathsf {D}^2_k$
is
![]() $(\mathsf {RT}^1_k)'$
, where
$(\mathsf {RT}^1_k)'$
, where
![]() $'$
is the Weihrauch jump operator (cf. [Reference Brattka, Gherardi and Pauly1, Definitions 6.8 and 6.9]). The following theorem may thus be compared against the previous one.
$'$
is the Weihrauch jump operator (cf. [Reference Brattka, Gherardi and Pauly1, Definitions 6.8 and 6.9]). The following theorem may thus be compared against the previous one.
Theorem 4.8. For every
![]() $k \geq 1$
,
$k \geq 1$
,
![]() $\mathsf {TT}^1_k \leq _{\mathrm {W}} \mathsf {D}^2_k$
.
$\mathsf {TT}^1_k \leq _{\mathrm {W}} \mathsf {D}^2_k$
.
Proof. The result is trivial for
![]() $k = 1$
, so we may assume
$k = 1$
, so we may assume
![]() $k \geq 2$
. Fix an instance
$k \geq 2$
. Fix an instance
![]() $f : 2^{<\omega } \to k$
of
$f : 2^{<\omega } \to k$
of
![]() $\mathsf {TT}^1_k$
. For each
$\mathsf {TT}^1_k$
. For each
![]() $n \in \omega $
and each
$n \in \omega $
and each
![]() $c < k-1$
we define a string
$c < k-1$
we define a string
![]() $\rho _{c,n} \in 2^{<\omega }$
by induction on c. Let
$\rho _{c,n} \in 2^{<\omega }$
by induction on c. Let
![]() $\rho _{-1,n} = \langle \rangle $
for definiteness, and assume that
$\rho _{-1,n} = \langle \rangle $
for definiteness, and assume that
![]() $\rho _{c-1,n}$
has been defined for some
$\rho _{c-1,n}$
has been defined for some
![]() $c < k-1$
. Then, let
$c < k-1$
. Then, let
![]() $\rho _{c,n}$
be the least extension of
$\rho _{c,n}$
be the least extension of
![]() $\rho _{c-1,n}$
(in some fixed enumeration of
$\rho _{c-1,n}$
(in some fixed enumeration of
![]() $2^{<\omega }$
) such that
$2^{<\omega }$
) such that
![]() $f(\sigma ) \neq c$
for all
$f(\sigma ) \neq c$
for all
![]() $\sigma \succeq \rho _{c,n}$
with
$\sigma \succeq \rho _{c,n}$
with
![]() $|\sigma | < n$
. Notice that
$|\sigma | < n$
. Notice that
![]() $\rho _{c,n}$
is always defined, and that it is uniformly computable from c and n. If
$\rho _{c,n}$
is always defined, and that it is uniformly computable from c and n. If
![]() $\lim _n \rho _{c,n}$
exists, we denote the limit by
$\lim _n \rho _{c,n}$
exists, we denote the limit by
![]() $\rho _c$
.
$\rho _c$
.
We next define a coloring
![]() $g : \omega \to k$
. Given
$g : \omega \to k$
. Given
![]() $n \in \omega $
, choose the largest
$n \in \omega $
, choose the largest
![]() $c < k$
such that
$c < k$
such that
![]() $\rho _{d,n} = \rho _{d,m}$
for all
$\rho _{d,n} = \rho _{d,m}$
for all
![]() $d < c$
and all
$d < c$
and all
![]() $m \geq n$
. (There is such a c because, in particular,
$m \geq n$
. (There is such a c because, in particular,
![]() $\rho _{-1,n} = \rho _{-1,m}$
for all
$\rho _{-1,n} = \rho _{-1,m}$
for all
![]() $m \geq n$
.) Then, let
$m \geq n$
.) Then, let
![]() $g(n) = c$
. Observe that g is uniformly computable from
$g(n) = c$
. Observe that g is uniformly computable from
![]() $f'$
, and so it is an instance of
$f'$
, and so it is an instance of
![]() $\mathsf {D}^2_k$
.
$\mathsf {D}^2_k$
.
Fix the largest
![]() $c < k$
such that
$c < k$
such that
![]() $\rho _d$
is defined for all
$\rho _d$
is defined for all
![]() $d < c$
. (Again, there is such a c because
$d < c$
. (Again, there is such a c because
![]() $\rho _{-1}$
is defined.) Then by definition of g, for all sufficiently large n we have that
$\rho _{-1}$
is defined.) Then by definition of g, for all sufficiently large n we have that
![]() $g(n) = c$
. Moreover, the set
$g(n) = c$
. Moreover, the set
![]() $\{ \sigma : f(\sigma ) = c \}$
must be dense above
$\{ \sigma : f(\sigma ) = c \}$
must be dense above
![]() $\rho _{c-1}$
. Suppose not. Then we may fix the least
$\rho _{c-1}$
. Suppose not. Then we may fix the least
![]() $\rho \succeq \rho _{c-1}$
such that
$\rho \succeq \rho _{c-1}$
such that
![]() $f(\sigma ) \neq c$
for all
$f(\sigma ) \neq c$
for all
![]() $\sigma \succeq \rho $
. Since
$\sigma \succeq \rho $
. Since
![]() $\rho _{-1,n} \preceq \cdots \preceq \rho _{c-1,n}$
for all n, we have
$\rho _{-1,n} \preceq \cdots \preceq \rho _{c-1,n}$
for all n, we have
![]() $\rho _{-1} \preceq \cdots \preceq \rho _{c-1}$
. Hence, by construction,
$\rho _{-1} \preceq \cdots \preceq \rho _{c-1}$
. Hence, by construction,
![]() $f(\sigma )> c$
for all
$f(\sigma )> c$
for all
![]() $\sigma \succeq \rho $
. It follows that
$\sigma \succeq \rho $
. It follows that
![]() $c < k-1$
and that
$c < k-1$
and that
![]() $\rho _{c,n} = \rho $
for all sufficiently large n. But then
$\rho _{c,n} = \rho $
for all sufficiently large n. But then
![]() $\rho _c$
is defined, a contradiction.
$\rho _c$
is defined, a contradiction.
To complete the proof, let M be any infinite monochromatic set for g, and let
![]() $n = \min M$
. By the argument above, the color of M under g must be c, so also
$n = \min M$
. By the argument above, the color of M under g must be c, so also
![]() $g(n) = c$
. By definition of g, this means that
$g(n) = c$
. By definition of g, this means that
![]() $\rho _{c-1,n} = \rho _{c-1,m}$
for all
$\rho _{c-1,n} = \rho _{c-1,m}$
for all
![]() $m \geq n$
, hence
$m \geq n$
, hence
![]() $\rho _{c-1,n} = \rho _{c-1}$
. Since
$\rho _{c-1,n} = \rho _{c-1}$
. Since
![]() $\{ \sigma : f(\sigma ) = c \}$
is dense above
$\{ \sigma : f(\sigma ) = c \}$
is dense above
![]() $\rho _{c-1}$
, we can uniformly compute from
$\rho _{c-1}$
, we can uniformly compute from
![]() $f \oplus M$
an
$f \oplus M$
an
![]() $H \cong 2^{<\omega }$
monochromatic for f with color c and root extending
$H \cong 2^{<\omega }$
monochromatic for f with color c and root extending
![]() $\rho _{c-1}$
.
$\rho _{c-1}$
.
5 Unbounded number of colors
We now turn to studying the problem
![]() $\mathsf {TT}^1_{\mathbb {N}}$
. As mentioned in the introduction, this is arguably the formulation closest to the principle
$\mathsf {TT}^1_{\mathbb {N}}$
. As mentioned in the introduction, this is arguably the formulation closest to the principle
![]() $\mathsf {TT}^1$
as it is studied in computability theory and reverse mathematics. Our main theorem here is Theorem 5.7, that
$\mathsf {TT}^1$
as it is studied in computability theory and reverse mathematics. Our main theorem here is Theorem 5.7, that
![]() ${}^1 \mathsf {TT}^1_{\mathbb {N}} \leq _{\mathrm {W}} \mathsf {RT}^1_{\mathbb {N}}$
. The proof requires some new combinatorial machinery which we first carefully develop.
${}^1 \mathsf {TT}^1_{\mathbb {N}} \leq _{\mathrm {W}} \mathsf {RT}^1_{\mathbb {N}}$
. The proof requires some new combinatorial machinery which we first carefully develop.
Definition 5.1. Fix a coloring f of
![]() $2^{<\omega }$
,
$2^{<\omega }$
,
![]() $k \geq 1$
, and
$k \geq 1$
, and
![]() $C = \{ c_0 < \cdots < c_{k-1} \} \subseteq \omega $
.
$C = \{ c_0 < \cdots < c_{k-1} \} \subseteq \omega $
.
-
(1) A C-rake for f is a set
 $R \subseteq 2^{<\omega }$
with the following properties.
$R \subseteq 2^{<\omega }$
with the following properties.-
• R is rooted.
-
• R is symmetric.
-
• If
 $\mathrm {rk}_R(\sigma ) \equiv i \mod k$
then
$\mathrm {rk}_R(\sigma ) \equiv i \mod k$
then
 $f(\sigma ) = c_i$
.
$f(\sigma ) = c_i$
. -
• If
 $\mathrm {rk}_R(\sigma ) \not \equiv k-1 \mod k$
then
$\mathrm {rk}_R(\sigma ) \not \equiv k-1 \mod k$
then
 $\sigma $
has exactly one successor in R.
$\sigma $
has exactly one successor in R. -
• If
 $\mathrm {rk}_R(\sigma ) \equiv k-1 \mod k$
then
$\mathrm {rk}_R(\sigma ) \equiv k-1 \mod k$
then
 $\sigma $
has
$\sigma $
has
 $0$
or
$0$
or
 $k+1$
many successors in R.
$k+1$
many successors in R.
-
-
(2) The block of
 $\sigma \in R$
in R, denoted
$\sigma \in R$
in R, denoted
 $\mathrm {bl}_R(\sigma )$
, is
$\mathrm {bl}_R(\sigma )$
, is
 $\lfloor \frac {\mathrm {rk}_R(\sigma )}{k} \rfloor $
.
$\lfloor \frac {\mathrm {rk}_R(\sigma )}{k} \rfloor $
. -
(3) R is good if
 $f(\sigma ) \in C$
for all
$f(\sigma ) \in C$
for all
 $\sigma \in 2^{<\omega }$
extending the root of R.
$\sigma \in 2^{<\omega }$
extending the root of R.
See Figure 1 for a typical example.

Figure 1 An illustration of a C-rake with
![]() $C = \{ 0,1,2 \}$
of height
$C = \{ 0,1,2 \}$
of height
![]() $9$
. The color under f of the nodes in blocks
$9$
. The color under f of the nodes in blocks
![]() $0$
and
$0$
and
![]() $1$
is indicated.
$1$
is indicated.
Lemma 5.2. Fix a computable coloring f of
![]() $2^{< \omega }$
, a non-empty finite set
$2^{< \omega }$
, a non-empty finite set
![]() $C \subseteq \omega $
, and a string
$C \subseteq \omega $
, and a string
![]() $\sigma \in 2^{<\omega }$
. There is a set
$\sigma \in 2^{<\omega }$
. There is a set
![]() $W_{f,C,\sigma } \subseteq C$
such that for some
$W_{f,C,\sigma } \subseteq C$
such that for some
![]() $\tau \succeq \sigma $
the following hold:
$\tau \succeq \sigma $
the following hold:
-
(1)
 $W_{f,C,\sigma }$
is uniformly
$W_{f,C,\sigma }$
is uniformly
 $\Sigma ^0_2$
in
$\Sigma ^0_2$
in
 $\sigma $
, a
$\sigma $
, a
 $\Delta ^0_1$
index for f, and a canonical index for C.
$\Delta ^0_1$
index for f, and a canonical index for C. -
(2)
 $\{ \rho \in 2^{<\omega } : f(\rho ) = c \}$
is dense above
$\{ \rho \in 2^{<\omega } : f(\rho ) = c \}$
is dense above
 $\tau $
for each
$\tau $
for each
 $c \in C \setminus W_{f,C,\sigma }$
.
$c \in C \setminus W_{f,C,\sigma }$
. -
(3)
 $f(\rho ) \notin W_{f,C,\sigma }$
for all
$f(\rho ) \notin W_{f,C,\sigma }$
for all
 $\rho \succeq \tau $
.
$\rho \succeq \tau $
.
Proof. We use a
![]() $\emptyset '$
oracle to enumerate
$\emptyset '$
oracle to enumerate
![]() $W_{f,C,\sigma }$
, letting
$W_{f,C,\sigma }$
, letting
![]() $W_{f,C,\sigma }[s]$
denote the set of elements enumerated by stage s. In parallel, we define
$W_{f,C,\sigma }[s]$
denote the set of elements enumerated by stage s. In parallel, we define
![]() $\tau $
by finitely many finite extensions of
$\tau $
by finitely many finite extensions of
![]() $\sigma $
. At stage
$\sigma $
. At stage
![]() $0$
, we set
$0$
, we set
![]() $\tau _0 = \sigma $
. At stage
$\tau _0 = \sigma $
. At stage
![]() $s> 0$
, we assume inductively that we have already defined
$s> 0$
, we assume inductively that we have already defined
![]() $\tau _{s-1}$
. We now check if there exists
$\tau _{s-1}$
. We now check if there exists
![]() $\tau ' < s$
extending
$\tau ' < s$
extending
![]() $\tau _{s-1}$
such that for some
$\tau _{s-1}$
such that for some
![]() $c \in C \setminus W_{f,C,\sigma }[s]$
we have that
$c \in C \setminus W_{f,C,\sigma }[s]$
we have that
![]() $f(\rho ) \neq c$
for all
$f(\rho ) \neq c$
for all
![]() $\rho \succeq \tau '$
. If so, we let
$\rho \succeq \tau '$
. If so, we let
![]() $\tau _s$
be the least such
$\tau _s$
be the least such
![]() $\tau '$
, and we enumerate all corresponding c into
$\tau '$
, and we enumerate all corresponding c into
![]() $W_{f,C,\sigma }$
. Otherwise, we let
$W_{f,C,\sigma }$
. Otherwise, we let
![]() $\tau _s = \tau _{s-1}$
. This completes the construction. We let
$\tau _s = \tau _{s-1}$
. This completes the construction. We let
![]() $\tau = \lim _s \tau _s$
. It is then easy to see that
$\tau = \lim _s \tau _s$
. It is then easy to see that
![]() $W_{f,C,\sigma }$
has the desired properties, as witnessed by
$W_{f,C,\sigma }$
has the desired properties, as witnessed by
![]() $\tau $
.
$\tau $
.
Observe that if f, C, and
![]() $\sigma $
above additionally satisfy that
$\sigma $
above additionally satisfy that
![]() $f(\rho ) \in C$
for all
$f(\rho ) \in C$
for all
![]() $\rho \succeq \sigma $
, then by part (3) of the lemma it follows that
$\rho \succeq \sigma $
, then by part (3) of the lemma it follows that
![]() $C \setminus W_{C,f,\sigma } \neq \emptyset $
. This is in particular the case if we are dealing with a good C-rake R for f of finite height, and where
$C \setminus W_{C,f,\sigma } \neq \emptyset $
. This is in particular the case if we are dealing with a good C-rake R for f of finite height, and where
![]() $\sigma $
is an extension of some leaf of R. We will use this fact repeatedly in the sequel.
$\sigma $
is an extension of some leaf of R. We will use this fact repeatedly in the sequel.
Lemma 5.3. Fix a computable coloring f of
![]() $2^{<\omega }$
. There exists a non-empty finite set
$2^{<\omega }$
. There exists a non-empty finite set
![]() $C \subseteq \omega $
and a computable good C-rake R for f of height
$C \subseteq \omega $
and a computable good C-rake R for f of height
![]() $\omega $
.
$\omega $
.
Proof. Let
![]() $W_{f,\operatorname {ran}(f),\langle \rangle }$
be as given by Lemma 5.2, as witnessed by
$W_{f,\operatorname {ran}(f),\langle \rangle }$
be as given by Lemma 5.2, as witnessed by
![]() $\tau $
. Define
$\tau $
. Define
![]() $C = \operatorname {ran}(f) \setminus W_{f,\operatorname {ran}(f),\langle \rangle }$
. As noted above, C is non-empty. By property (2), we can computably construct a C-rake R for f of height
$C = \operatorname {ran}(f) \setminus W_{f,\operatorname {ran}(f),\langle \rangle }$
. As noted above, C is non-empty. By property (2), we can computably construct a C-rake R for f of height
![]() $\omega $
with root
$\omega $
with root
![]() $\tau $
. By property (3), R is good.
$\tau $
. By property (3), R is good.
We now give a definition of a useful way to “pick out” monochromatic subtrees from rakes.
Definition 5.4. Fix a coloring f of
![]() $2^{<\omega }$
, a non-empty finite set
$2^{<\omega }$
, a non-empty finite set
![]() $C \subseteq \omega $
, a C-rake R for f (of finite or infinite height), and a set
$C \subseteq \omega $
, a C-rake R for f (of finite or infinite height), and a set
![]() $S \subseteq 2^{<\omega }$
. We write
$S \subseteq 2^{<\omega }$
. We write
![]() $S \trianglelefteq R$
if the following properties hold.
$S \trianglelefteq R$
if the following properties hold.
-
(1)
 $S \subseteq R$
.
$S \subseteq R$
. -
(2)
 $S \cong 2^{< n}$
for some
$S \cong 2^{< n}$
for some
 $n \leq \mathrm {ht}(R)$
. (Note that we may have
$n \leq \mathrm {ht}(R)$
. (Note that we may have
 $n = \mathrm {ht}(R) = \omega $
.)
$n = \mathrm {ht}(R) = \omega $
.) -
(3)
 $\mathrm {rk}_S(\sigma ) = \mathrm {bl}_R(\sigma )$
for all
$\mathrm {rk}_S(\sigma ) = \mathrm {bl}_R(\sigma )$
for all
 $\sigma \in S$
.
$\sigma \in S$
. -
(4)
 $\mathrm {rk}_R(\sigma ) \equiv \mathrm {rk}_R(\tau ) \mod |C|$
for all
$\mathrm {rk}_R(\sigma ) \equiv \mathrm {rk}_R(\tau ) \mod |C|$
for all
 $\sigma ,\tau \in S$
.
$\sigma ,\tau \in S$
.
The definition ensures that S is symmetric, that strings with the same rank in S are in the same block of R, and that all elements of S have the same rank in R modulo
![]() $|C|$
and therefore have the same color under f. See Figure 2 for an illustration. Observe that if R has finite height, and
$|C|$
and therefore have the same color under f. See Figure 2 for an illustration. Observe that if R has finite height, and
![]() $S \trianglelefteq R$
for some S of height
$S \trianglelefteq R$
for some S of height
![]() $\mathrm {ht}(R)/|C|$
, then for every leaf
$\mathrm {ht}(R)/|C|$
, then for every leaf
![]() $\sigma $
of S there is a unique leaf
$\sigma $
of S there is a unique leaf
![]() $\lambda $
of R such that
$\lambda $
of R such that
![]() $\sigma \preceq \lambda $
.
$\sigma \preceq \lambda $
.

Figure 2 A C-rake with
![]() $|C|=3$
(represented by hollow nodes, connected by interrupted lines), and a set
$|C|=3$
(represented by hollow nodes, connected by interrupted lines), and a set
![]() $S \trianglelefteq R$
of height
$S \trianglelefteq R$
of height
![]() $3$
(represented by solid nodes, connected by uninterrupted lines).
$3$
(represented by solid nodes, connected by uninterrupted lines).
We proceed with two technical lemmas that will round out the set of tools we need.
Lemma 5.5. Fix a computable coloring f of
![]() $2^{<\omega }$
, a non-empty finite set
$2^{<\omega }$
, a non-empty finite set
![]() $C \subseteq \omega $
, and a good C-rake R for f of finite height. For each leaf
$C \subseteq \omega $
, and a good C-rake R for f of finite height. For each leaf
![]() $\lambda $
of R, fix
$\lambda $
of R, fix
![]() $c_\lambda \in C \setminus W_{f,C,\lambda }$
(where
$c_\lambda \in C \setminus W_{f,C,\lambda }$
(where
![]() $W_{f,C,\lambda }$
is as given by Lemma 5.2).
$W_{f,C,\lambda }$
is as given by Lemma 5.2).
-
(1) There exists
 $c \in \{ c_\lambda : \lambda \text { a leaf of } R \}$
and an
$c \in \{ c_\lambda : \lambda \text { a leaf of } R \}$
and an
 $H \cong 2^{<\omega }$
monochromatic for f with color c such that
$H \cong 2^{<\omega }$
monochromatic for f with color c such that
 $H^{\mathrm {rk} < \mathrm {ht}(R)/|C|} \trianglelefteq R$
and
$H^{\mathrm {rk} < \mathrm {ht}(R)/|C|} \trianglelefteq R$
and
 $c_\lambda = c$
for every leaf
$c_\lambda = c$
for every leaf
 $\lambda $
of R extending a leaf of
$\lambda $
of R extending a leaf of
 $H^{\mathrm {rk} < \mathrm {ht}(R)/|C|}$
.
$H^{\mathrm {rk} < \mathrm {ht}(R)/|C|}$
. -
(2) There is a computable procedure, uniform in canonical indices for C, R, and
 $\{ c_\lambda : \lambda \text { a leaf of } R \}$
, that outputs some c as above and a canonical index for the initial segment
$\{ c_\lambda : \lambda \text { a leaf of } R \}$
, that outputs some c as above and a canonical index for the initial segment
 $H^{\mathrm {rk} < \mathrm {ht}(R)/|C|}$
for some H as above.
$H^{\mathrm {rk} < \mathrm {ht}(R)/|C|}$
for some H as above.
Proof. Say
![]() $|C| = k$
, so that
$|C| = k$
, so that
![]() $\mathrm {ht}(R) = mk$
for some
$\mathrm {ht}(R) = mk$
for some
![]() $m \geq 1$
. We define a map
$m \geq 1$
. We define a map
![]() $g : R \to C$
by reverse induction on rank. For each element of R of maximum rank, which is to say, for each leaf
$g : R \to C$
by reverse induction on rank. For each element of R of maximum rank, which is to say, for each leaf
![]() $\lambda $
, we let
$\lambda $
, we let
![]() $g(\lambda ) = c_\lambda $
. Next, fix
$g(\lambda ) = c_\lambda $
. Next, fix
![]() $\sigma \in R$
that is not a leaf and suppose we have defined g on all elements of R of larger rank. If
$\sigma \in R$
that is not a leaf and suppose we have defined g on all elements of R of larger rank. If
![]() $\sigma $
has a unique successor
$\sigma $
has a unique successor
![]() $\tau $
in R, let
$\tau $
in R, let
![]() $g(\sigma ) = g(\tau )$
. Otherwise, since R is a C-rake,
$g(\sigma ) = g(\tau )$
. Otherwise, since R is a C-rake,
![]() $\sigma $
has
$\sigma $
has
![]() $k+1$
many successors
$k+1$
many successors
![]() $\tau _0,\ldots ,\tau _{k}$
in R. We can thus computably choose a
$\tau _0,\ldots ,\tau _{k}$
in R. We can thus computably choose a
![]() $c \in C$
such that
$c \in C$
such that
![]() $g(\tau _i) = g(\tau _j) = c$
for some distinct
$g(\tau _i) = g(\tau _j) = c$
for some distinct
![]() $i,j \leq k$
. Let
$i,j \leq k$
. Let
![]() $g(\sigma ) = c$
. This completes the definition. Notice that for all
$g(\sigma ) = c$
. This completes the definition. Notice that for all
![]() $\sigma \preceq \tau $
in R, if
$\sigma \preceq \tau $
in R, if
![]() $\mathrm {bl}_R(\sigma ) = \mathrm {bl}_R(\tau )$
then
$\mathrm {bl}_R(\sigma ) = \mathrm {bl}_R(\tau )$
then
![]() $g(\sigma ) = g(\tau )$
.
$g(\sigma ) = g(\tau )$
.
Now fix the color
![]() $c \in C$
that g assigns to the root of R. We define
$c \in C$
that g assigns to the root of R. We define
![]() $h : 2^{< m} \to R$
by induction on finite strings. Let
$h : 2^{< m} \to R$
by induction on finite strings. Let
![]() $h(\langle \rangle )$
be the shortest
$h(\langle \rangle )$
be the shortest
![]() $\sigma \in R$
with
$\sigma \in R$
with
![]() $f(\sigma ) = c$
. Since R is a C-rake, we have that
$f(\sigma ) = c$
. Since R is a C-rake, we have that
![]() $\mathrm {bl}_R(h(\langle \rangle )) = 0$
, and so also
$\mathrm {bl}_R(h(\langle \rangle )) = 0$
, and so also
![]() $g(h(\langle \rangle )) = c$
, by construction of g. Suppose next that we have defined
$g(h(\langle \rangle )) = c$
, by construction of g. Suppose next that we have defined
![]() $h(\alpha ) \in R$
for some string
$h(\alpha ) \in R$
for some string
![]() $\alpha $
with
$\alpha $
with
![]() $|\alpha | < m-1$
. Assume inductively that
$|\alpha | < m-1$
. Assume inductively that
![]() $\mathrm {bl}_R(h(\alpha )) = |\alpha |$
and that
$\mathrm {bl}_R(h(\alpha )) = |\alpha |$
and that
![]() $f(h(\alpha )) = g(h(\alpha )) = c$
. Thus
$f(h(\alpha )) = g(h(\alpha )) = c$
. Thus
![]() $h(\alpha )$
is not a leaf of R, nor in the same block as a leaf, since
$h(\alpha )$
is not a leaf of R, nor in the same block as a leaf, since
![]() $\mathrm {bl}_R(\lambda ) = m-1$
for all leaves
$\mathrm {bl}_R(\lambda ) = m-1$
for all leaves
![]() $\lambda $
of R. By construction of g,
$\lambda $
of R. By construction of g,
![]() $h(\alpha )$
has two extensions
$h(\alpha )$
has two extensions
![]() $\tau ,\tau ' \in R$
such that
$\tau ,\tau ' \in R$
such that
![]() $\mathrm {bl}_R(\tau ) = \mathrm {bl}_R(\tau ') = \mathrm {bl}_R(h(\alpha )) + 1$
and
$\mathrm {bl}_R(\tau ) = \mathrm {bl}_R(\tau ') = \mathrm {bl}_R(h(\alpha )) + 1$
and
![]() $g(\tau ) = g(\tau ') = c$
, and we may assume that
$g(\tau ) = g(\tau ') = c$
, and we may assume that
![]() $\tau ,\tau '$
are of minimal length with these properties (i.e., they are the shortest elements of the next block after that of
$\tau ,\tau '$
are of minimal length with these properties (i.e., they are the shortest elements of the next block after that of
![]() $h(\alpha )$
). Let
$h(\alpha )$
). Let
![]() $h(\alpha 0)$
and
$h(\alpha 0)$
and
![]() $h(\alpha 1)$
be the shortest incomparable
$h(\alpha 1)$
be the shortest incomparable
![]() $\sigma \succeq \tau $
and
$\sigma \succeq \tau $
and
![]() $\sigma ' \succeq \tau '$
in R with
$\sigma ' \succeq \tau '$
in R with
![]() $f(\sigma ) = f(\sigma ') = c$
. As above, we have for each
$f(\sigma ) = f(\sigma ') = c$
. As above, we have for each
![]() $i < 2$
that
$i < 2$
that
![]() $\mathrm {bl}_R(h(\alpha i)) = \mathrm {bl}_R(h(\alpha )) + 1 =|\alpha | + 1$
and
$\mathrm {bl}_R(h(\alpha i)) = \mathrm {bl}_R(h(\alpha )) + 1 =|\alpha | + 1$
and
![]() $f(h(\alpha i)) = g(h(\alpha i)) = c$
, so the inductive assumptions are maintained.
$f(h(\alpha i)) = g(h(\alpha i)) = c$
, so the inductive assumptions are maintained.
Let
![]() $S = \operatorname {ran}(h)$
. Then
$S = \operatorname {ran}(h)$
. Then
![]() $S \cong 2^{< m}$
as witnessed by h, and S is monochromatic for f with color c. It follows from the construction that
$S \cong 2^{< m}$
as witnessed by h, and S is monochromatic for f with color c. It follows from the construction that
![]() $S \trianglelefteq R$
. Consider any leaf
$S \trianglelefteq R$
. Consider any leaf
![]() $\sigma $
of S, and let
$\sigma $
of S, and let
![]() $\lambda $
be the unique leaf of R extending
$\lambda $
be the unique leaf of R extending
![]() $\sigma $
. Since
$\sigma $
. Since
![]() $\mathrm {bl}_R(\sigma ) = \mathrm {bl}_R(\lambda )$
, we have that
$\mathrm {bl}_R(\sigma ) = \mathrm {bl}_R(\lambda )$
, we have that
![]() $c = f(\sigma ) = g(\sigma ) = g(\lambda ) = c_{\lambda }$
. Moreover, since
$c = f(\sigma ) = g(\sigma ) = g(\lambda ) = c_{\lambda }$
. Moreover, since
![]() $c = c_{\lambda } \in C \setminus W_{C,f,\lambda }$
, it follows by Lemma 5.2 (2) that
$c = c_{\lambda } \in C \setminus W_{C,f,\lambda }$
, it follows by Lemma 5.2 (2) that
![]() $\{ \rho \in 2^{<\omega } : f(\rho ) = c \}$
is dense above some extension of
$\{ \rho \in 2^{<\omega } : f(\rho ) = c \}$
is dense above some extension of
![]() $\lambda $
.
$\lambda $
.
For each leaf
![]() $\lambda $
of R extending a leaf of S there therefore exists an
$\lambda $
of R extending a leaf of S there therefore exists an
![]() $H_\lambda \cong 2^{<\omega }$
monochromatic for f with color c and with root
$H_\lambda \cong 2^{<\omega }$
monochromatic for f with color c and with root
![]() $\rho _\lambda \succeq \lambda $
. Define
$\rho _\lambda \succeq \lambda $
. Define
 $$\begin{align*}H = S \cup \left( \bigcup_{\substack{\lambda \text{ a leaf of } R\\ \text{ extending a}\\ \text{leaf of } S}} H_\lambda \setminus \{ \rho_{\lambda} \} \right). \end{align*}$$
$$\begin{align*}H = S \cup \left( \bigcup_{\substack{\lambda \text{ a leaf of } R\\ \text{ extending a}\\ \text{leaf of } S}} H_\lambda \setminus \{ \rho_{\lambda} \} \right). \end{align*}$$
Then
![]() $H \cong 2^{<\omega }$
, H is monochromatic for f with color c, and
$H \cong 2^{<\omega }$
, H is monochromatic for f with color c, and
![]() $H^{\mathrm {rk} < \mathrm {ht}(R)/|C|} = H^{\mathrm {rk} < m} = S$
satisfies the conclusion of part (1).
$H^{\mathrm {rk} < \mathrm {ht}(R)/|C|} = H^{\mathrm {rk} < m} = S$
satisfies the conclusion of part (1).
Finally, note that k, m, and the function g are all uniformly computable from canonical indices for C, R, and the set
![]() $\{ c_\lambda : \lambda \text { a leaf of } R \}$
. Hence, so is the color assigned by g to the root of R, which is c, and from here we can uniformly compute the function
$\{ c_\lambda : \lambda \text { a leaf of } R \}$
. Hence, so is the color assigned by g to the root of R, which is c, and from here we can uniformly compute the function
![]() $h : 2^{< m} \to R$
. Since
$h : 2^{< m} \to R$
. Since
![]() $H^{\mathrm {rk} < \mathrm {ht}(R)/|C|} = \operatorname {ran}(h)$
, and h is strictly increasing under
$H^{\mathrm {rk} < \mathrm {ht}(R)/|C|} = \operatorname {ran}(h)$
, and h is strictly increasing under
![]() $\preceq $
, this completes the proof.
$\preceq $
, this completes the proof.
Lemma 5.6. Fix a computable coloring f of
![]() $2^{<\omega }$
and a
$2^{<\omega }$
and a
![]() $\Sigma ^0_1$
property
$\Sigma ^0_1$
property
![]() $\varphi $
of finite subsets of
$\varphi $
of finite subsets of
![]() $2^{<\omega }$
such that whenever
$2^{<\omega }$
such that whenever
![]() $H \cong 2^{<\omega }$
is monochromatic for f then
$H \cong 2^{<\omega }$
is monochromatic for f then
![]() $\varphi (H^{\mathrm {rk} <n})$
holds for some n. There exists a non-empty finite set
$\varphi (H^{\mathrm {rk} <n})$
holds for some n. There exists a non-empty finite set
![]() $C \subseteq \omega $
and a good C-rake R for f of finite height such that for every
$C \subseteq \omega $
and a good C-rake R for f of finite height such that for every
![]() $H \cong 2^{<\omega }$
monochromatic for f with
$H \cong 2^{<\omega }$
monochromatic for f with
![]() $H^{\mathrm {rk} < \mathrm {ht}(R)/|C|} \trianglelefteq R$
we have that
$H^{\mathrm {rk} < \mathrm {ht}(R)/|C|} \trianglelefteq R$
we have that
![]() $\varphi (H^{\mathrm {rk} < \mathrm {ht}(R)/|C|})$
holds.
$\varphi (H^{\mathrm {rk} < \mathrm {ht}(R)/|C|})$
holds.
Proof. Apply Lemma 5.3 to obtain a non-empty finite set
![]() $C \subseteq \omega $
and a computable good C-rake
$C \subseteq \omega $
and a computable good C-rake
![]() $R_0$
for f of height
$R_0$
for f of height
![]() $\omega $
. Let
$\omega $
. Let
![]() $\mathcal {P}$
be the class of all
$\mathcal {P}$
be the class of all
![]() $H \trianglelefteq R_0$
such that H has height
$H \trianglelefteq R_0$
such that H has height
![]() $\omega $
and is monochromatic for f. Notice that
$\omega $
and is monochromatic for f. Notice that
![]() $\mathcal {P}$
is a
$\mathcal {P}$
is a
![]() $\Pi ^0_1$
class. The only part of the definition for which this may not be immediately apparent is the stipulation that each
$\Pi ^0_1$
class. The only part of the definition for which this may not be immediately apparent is the stipulation that each
![]() $H \in \mathcal {P}$
has height
$H \in \mathcal {P}$
has height
![]() $\omega $
, and so in particular, that each element of H has a pair of incomparable successors in H. But since we want
$\omega $
, and so in particular, that each element of H has a pair of incomparable successors in H. But since we want
![]() $H \trianglelefteq R_0$
, the latter condition can be expressed as
$H \trianglelefteq R_0$
, the latter condition can be expressed as
And since the set of all elements in
![]() $R_0$
in any given block is finite, the above is
$R_0$
in any given block is finite, the above is
![]() $\Pi ^0_1$
.
$\Pi ^0_1$
.
Since
![]() $R_0$
has height
$R_0$
has height
![]() $\omega $
, it follows that for each
$\omega $
, it follows that for each
![]() $c \in C$
there exists
$c \in C$
there exists
![]() $H \in \mathcal {P}$
monochromatic for f with color c, so in particular
$H \in \mathcal {P}$
monochromatic for f with color c, so in particular
![]() $\mathcal {P} \neq \emptyset $
. Now, let
$\mathcal {P} \neq \emptyset $
. Now, let
![]() $\mathcal {Q}$
be the class of all
$\mathcal {Q}$
be the class of all
![]() $H \in \mathcal {P}$
such that
$H \in \mathcal {P}$
such that
![]() $\neg \varphi (H^{\mathrm {rk} < n})$
holds for all n. This is again a
$\neg \varphi (H^{\mathrm {rk} < n})$
holds for all n. This is again a
![]() $\Pi ^0_1$
class, and by hypothesis,
$\Pi ^0_1$
class, and by hypothesis,
![]() $\mathcal {Q} = \emptyset $
. By compactness of Cantor space, we can fix an
$\mathcal {Q} = \emptyset $
. By compactness of Cantor space, we can fix an
![]() $m \in \omega $
such that for every
$m \in \omega $
such that for every
![]() $H \in \mathcal {P}$
there exists
$H \in \mathcal {P}$
there exists
![]() $n \leq m$
for which
$n \leq m$
for which
![]() $\varphi (H^{\mathrm {rk} < n})$
holds. Let
$\varphi (H^{\mathrm {rk} < n})$
holds. Let
![]() $R = R_0^{\mathrm {rk} < m|C|}$
, a good C-rake of finite height. If
$R = R_0^{\mathrm {rk} < m|C|}$
, a good C-rake of finite height. If
![]() $H \cong 2^{<\omega }$
is any set monochromatic for f and satisfying
$H \cong 2^{<\omega }$
is any set monochromatic for f and satisfying
![]() $H^{\mathrm {rk} < m} \trianglelefteq R$
, then there must be a
$H^{\mathrm {rk} < m} \trianglelefteq R$
, then there must be a
![]() $G \in \mathcal {P}$
so that
$G \in \mathcal {P}$
so that
![]() $H^{\mathrm {rk} < m} = G^{\mathrm {rk} < m}$
. Thus,
$H^{\mathrm {rk} < m} = G^{\mathrm {rk} < m}$
. Thus,
![]() $\varphi (H^{\mathrm {rk} < n})$
holds for some
$\varphi (H^{\mathrm {rk} < n})$
holds for some
![]() $n \leq m = \mathrm {ht}(R)/|C|$
, as was to be shown. By our use conventions (Section 2), this implies that
$n \leq m = \mathrm {ht}(R)/|C|$
, as was to be shown. By our use conventions (Section 2), this implies that
![]() $\varphi (H^{\mathrm {rk} < \mathrm {ht}(R)/|C|})$
holds as well.
$\varphi (H^{\mathrm {rk} < \mathrm {ht}(R)/|C|})$
holds as well.
We can now assemble the pieces to prove our main theorem.
Theorem 5.7.
![]() ${}^1 \mathsf {TT}^1_{\mathbb {N}} \leq _{\mathrm {W}} \mathsf {RT}^1_{\mathbb {N}}$
.
${}^1 \mathsf {TT}^1_{\mathbb {N}} \leq _{\mathrm {W}} \mathsf {RT}^1_{\mathbb {N}}$
.
Proof. Consider an arbitrary instance
![]() $\langle A,\Delta ,\Gamma \rangle $
of
$\langle A,\Delta ,\Gamma \rangle $
of
![]() ${}^1\mathsf {TT}^1_{\mathbb {N}}$
. We have that
${}^1\mathsf {TT}^1_{\mathbb {N}}$
. We have that
![]() $\Delta (A)$
is a coloring f of
$\Delta (A)$
is a coloring f of
![]() $2^{<\omega }$
, and if
$2^{<\omega }$
, and if
![]() $H \cong 2^{<\omega }$
is any monochromatic set for f then
$H \cong 2^{<\omega }$
is any monochromatic set for f then
![]() $\Gamma (A, H)(0) \downarrow $
, and the output of this computation is a solution to
$\Gamma (A, H)(0) \downarrow $
, and the output of this computation is a solution to
![]() $\langle A,\Delta ,\Gamma \rangle $
. We define an instance d of
$\langle A,\Delta ,\Gamma \rangle $
. We define an instance d of
![]() $\mathsf {RT}^1_{\mathbb {N}}$
, uniformly computable from
$\mathsf {RT}^1_{\mathbb {N}}$
, uniformly computable from
![]() $\langle A,\Delta ,\Gamma \rangle $
, such that if M is any infinite homogeneous set for d then
$\langle A,\Delta ,\Gamma \rangle $
, such that if M is any infinite homogeneous set for d then
![]() $\langle A,\Delta ,\Gamma \rangle \oplus M$
uniformly computes
$\langle A,\Delta ,\Gamma \rangle \oplus M$
uniformly computes
![]() $\Gamma (A, H)(0)$
for some such H.
$\Gamma (A, H)(0)$
for some such H.
To begin, we claim that there exists a non-empty finite set
![]() $C \subseteq \omega $
, a good C-rake R for f of finite height, and an
$C \subseteq \omega $
, a good C-rake R for f of finite height, and an
![]() $s \in \omega $
with the following properties. For each leaf
$s \in \omega $
with the following properties. For each leaf
![]() $\lambda $
of R, and each choice of
$\lambda $
of R, and each choice of
![]() $c_\lambda \in C \setminus W_{f,C,\lambda }[s]$
, we apply Lemma 5.5 (2), relativized to A. This specifies an A-computable procedure for determining a
$c_\lambda \in C \setminus W_{f,C,\lambda }[s]$
, we apply Lemma 5.5 (2), relativized to A. This specifies an A-computable procedure for determining a
![]() $c \in \{ c_\lambda : \lambda \text { a leaf of } R \}$
and a finite set
$c \in \{ c_\lambda : \lambda \text { a leaf of } R \}$
and a finite set
![]() $S \trianglelefteq R$
of height
$S \trianglelefteq R$
of height
![]() $\mathrm {ht}(R)/|C|$
that is monochromatic for f with color c and such that
$\mathrm {ht}(R)/|C|$
that is monochromatic for f with color c and such that
![]() $c_\lambda = c$
for every leaf
$c_\lambda = c$
for every leaf
![]() $\lambda $
of R extending a leaf of S. The properties of C, R, and s are that this procedure halts, and that for the resulting S we have that
$\lambda $
of R extending a leaf of S. The properties of C, R, and s are that this procedure halts, and that for the resulting S we have that
![]() $\Gamma (A,S)(0) \downarrow $
.
$\Gamma (A,S)(0) \downarrow $
.
Note that the procedure from the lemma need not halt for arbitrary s, since we may have
![]() $W_{f,C,\lambda }[s] \subset W_{f,C,\lambda }$
for some
$W_{f,C,\lambda }[s] \subset W_{f,C,\lambda }$
for some
![]() $\lambda $
and therefore it could be that some
$\lambda $
and therefore it could be that some
![]() $c_\lambda $
actually belongs to
$c_\lambda $
actually belongs to
![]() $W_{f,C,\lambda }$
. (Thus, the hypotheses of the lemma would not be met.) Likewise, nothing about the lemma guarantees that if the procedure halts and outputs c and S then necessarily
$W_{f,C,\lambda }$
. (Thus, the hypotheses of the lemma would not be met.) Likewise, nothing about the lemma guarantees that if the procedure halts and outputs c and S then necessarily
![]() $\Gamma (A,S)(0) \downarrow $
.
$\Gamma (A,S)(0) \downarrow $
.
To prove the claim, note that if we take
![]() $\varphi (X)$
to be the
$\varphi (X)$
to be the
![]() $\Sigma ^0_1(A)$
formula stating that
$\Sigma ^0_1(A)$
formula stating that
![]() $\Gamma (A,X)(0) \downarrow $
, then f and
$\Gamma (A,X)(0) \downarrow $
, then f and
![]() $\varphi $
are precisely as in the hypothesis of Lemma 5.6, relativized to A. Thus, there exists a non-empty finite set
$\varphi $
are precisely as in the hypothesis of Lemma 5.6, relativized to A. Thus, there exists a non-empty finite set
![]() $C \subseteq \omega $
and a good C-rake R for f of finite height such that for for every
$C \subseteq \omega $
and a good C-rake R for f of finite height such that for for every
![]() $H \cong 2^{<\omega }$
monochromatic for f with
$H \cong 2^{<\omega }$
monochromatic for f with
![]() $H^{\mathrm {rk} < \mathrm {ht}(R)/|C|} \trianglelefteq R$
we have
$H^{\mathrm {rk} < \mathrm {ht}(R)/|C|} \trianglelefteq R$
we have
![]() $\Gamma (A,H^{\mathrm {rk} < \mathrm {ht}(R)/|C|}) \downarrow $
.
$\Gamma (A,H^{\mathrm {rk} < \mathrm {ht}(R)/|C|}) \downarrow $
.
At the same time, by Lemma 5.5, for every choice of
![]() $c_\lambda \in C \setminus W_{f,C,\lambda }$
for
$c_\lambda \in C \setminus W_{f,C,\lambda }$
for
![]() $\lambda $
a leaf of R, there is a
$\lambda $
a leaf of R, there is a
![]() $c \in \{ c_\lambda : \lambda \text { a leaf of } R \}$
and an
$c \in \{ c_\lambda : \lambda \text { a leaf of } R \}$
and an
![]() $H \cong 2^{<\omega }$
monochromatic for f with color c such that
$H \cong 2^{<\omega }$
monochromatic for f with color c such that
![]() $H^{\mathrm {rk} < \mathrm {ht}(R)/|C|} \trianglelefteq R$
and
$H^{\mathrm {rk} < \mathrm {ht}(R)/|C|} \trianglelefteq R$
and
![]() $c_\lambda = c$
for every leaf
$c_\lambda = c$
for every leaf
![]() $\lambda $
of R extending a leaf of
$\lambda $
of R extending a leaf of
![]() $H \cong 2^{<\omega }$
. Thus, in particular for this H, we have that
$H \cong 2^{<\omega }$
. Thus, in particular for this H, we have that
![]() $\Gamma (A,H^{\mathrm {rk} < \mathrm {ht}(R)/|C|}) \downarrow $
. But c and
$\Gamma (A,H^{\mathrm {rk} < \mathrm {ht}(R)/|C|}) \downarrow $
. But c and
![]() $H^{\mathrm {rk} < \mathrm {ht}(R)/|C|}$
are the number and finite set produced by the computable procedure in part (2) of that lemma. Hence, if s is large enough so that
$H^{\mathrm {rk} < \mathrm {ht}(R)/|C|}$
are the number and finite set produced by the computable procedure in part (2) of that lemma. Hence, if s is large enough so that
![]() $W_{f,C,\lambda }[s] = W_{f,C,\lambda }$
for all leaves
$W_{f,C,\lambda }[s] = W_{f,C,\lambda }$
for all leaves
![]() $\lambda $
of R, then C, R, and s are as desired. The claim is proved.
$\lambda $
of R, then C, R, and s are as desired. The claim is proved.
The definition of C, R, and s in the statement of the claim is uniformly
![]() $\Delta ^0_2$
in
$\Delta ^0_2$
in
![]() $\langle A,\Delta ,\Gamma \rangle $
. Hence, uniformly computably in
$\langle A,\Delta ,\Gamma \rangle $
. Hence, uniformly computably in
![]() $\langle A,\Delta ,\Gamma \rangle $
, we can approximate the least such C, R, and s by some
$\langle A,\Delta ,\Gamma \rangle $
, we can approximate the least such C, R, and s by some
![]() $\langle C_t: t \in \omega \rangle $
,
$\langle C_t: t \in \omega \rangle $
,
![]() $\langle R_t: t \in \omega \rangle $
, and
$\langle R_t: t \in \omega \rangle $
, and
![]() $\langle s_t: t \in \omega \rangle $
. That is, for each t,
$\langle s_t: t \in \omega \rangle $
. That is, for each t,
![]() $C_t$
and
$C_t$
and
![]() $R_t$
are canonical indices of finite sets,
$R_t$
are canonical indices of finite sets,
![]() $s_t$
is a number, and we have that
$s_t$
is a number, and we have that
![]() $\lim _t C_t = C$
,
$\lim _t C_t = C$
,
![]() $\lim _t R_t = R$
, and
$\lim _t R_t = R$
, and
![]() $\lim _t s_t = s$
. Of course,
$\lim _t s_t = s$
. Of course,
![]() $R_t$
need not be good, or even a
$R_t$
need not be good, or even a
![]() $C_t$
-rake, other than in the limit. Let
$C_t$
-rake, other than in the limit. Let
![]() $n_t$
denote the number of leaves of
$n_t$
denote the number of leaves of
![]() $R_t$
.
$R_t$
.
By Lemma 5.2 (1), relativized to A, we have that for each
![]() $t \in \omega $
and
$t \in \omega $
and
![]() $i < n_t$
the set
$i < n_t$
the set
![]() $W_{f,C_t,\lambda _i}$
is
$W_{f,C_t,\lambda _i}$
is
![]() $\Sigma ^0_2(A)$
uniformly in f,
$\Sigma ^0_2(A)$
uniformly in f,
![]() $C_t$
and
$C_t$
and
![]() $\lambda _i$
. This means
$\lambda _i$
. This means
![]() $W_{f,C_t,\lambda _i}$
can be A-computably approximated by a sequence of finite sets
$W_{f,C_t,\lambda _i}$
can be A-computably approximated by a sequence of finite sets
![]() $\langle V_{t,i,u} : u \in \omega \rangle $
, uniformly in
$\langle V_{t,i,u} : u \in \omega \rangle $
, uniformly in
![]() $C_t$
and
$C_t$
and
![]() $\lambda _i$
. More precisely,
$\lambda _i$
. More precisely,
![]() $V_{t,i,u} \subseteq C_t$
for all u, and for each
$V_{t,i,u} \subseteq C_t$
for all u, and for each
![]() $c \in C_t$
we have that
$c \in C_t$
we have that
![]() $c \in V_{t,i,u}$
for cofinitely many u if and only if
$c \in V_{t,i,u}$
for cofinitely many u if and only if
![]() $c \in W_{f,C_t,\lambda _i}$
. By removing the least element whose membership in
$c \in W_{f,C_t,\lambda _i}$
. By removing the least element whose membership in
![]() $V_{t,i,u}$
has changed most recently (with respect to u), or the least element if none such exists, we may further assume that
$V_{t,i,u}$
has changed most recently (with respect to u), or the least element if none such exists, we may further assume that
![]() $C_t \setminus V_{t,i,u} \neq \emptyset $
for all u. (If t happens to be large enough that
$C_t \setminus V_{t,i,u} \neq \emptyset $
for all u. (If t happens to be large enough that
![]() $C_t = C$
and
$C_t = C$
and
![]() $R_t = R$
, then
$R_t = R$
, then
![]() $C_t \setminus W_{f,C_t,\lambda _i} \neq \emptyset $
since R is a good C-rake for f. Then since
$C_t \setminus W_{f,C_t,\lambda _i} \neq \emptyset $
since R is a good C-rake for f. Then since
![]() $V_{t,i,u} \supseteq W_{f,C_t,\lambda _i}$
for all sufficiently large u, any such element removed will indeed belong to
$V_{t,i,u} \supseteq W_{f,C_t,\lambda _i}$
for all sufficiently large u, any such element removed will indeed belong to
![]() $C_t \setminus V_{t,i,u}$
for any such u.)
$C_t \setminus V_{t,i,u}$
for any such u.)
We now construct a coloring
![]() $d : \omega \to \omega $
. (We will argue below that this is actually an instance of
$d : \omega \to \omega $
. (We will argue below that this is actually an instance of
![]() $\mathsf {RT}^1_{\mathbb {N}}$
.) Fix t; we define
$\mathsf {RT}^1_{\mathbb {N}}$
.) Fix t; we define
![]() $d(t)$
. First, compute
$d(t)$
. First, compute
![]() $C_t$
,
$C_t$
,
![]() $R_t$
, and
$R_t$
, and
![]() $s_t$
, and let
$s_t$
, and let
![]() $\lambda _0,\ldots ,\lambda _{n_t-1}$
be the leaves of
$\lambda _0,\ldots ,\lambda _{n_t-1}$
be the leaves of
![]() $R_t$
, enumerated in lexicographic order. Then, for each
$R_t$
, enumerated in lexicographic order. Then, for each
![]() $i < n_t$
, let
$i < n_t$
, let
![]() $c_i$
be the least element of
$c_i$
be the least element of
![]() $C_t \setminus V_{t,i,t}$
, which is non-empty as discussed above. Finally, we define
$C_t \setminus V_{t,i,t}$
, which is non-empty as discussed above. Finally, we define
![]() $d(t) = \langle C_t,R_t,c_0,\ldots ,c_{n_t-1} \rangle $
. Clearly, d is uniformly computable from
$d(t) = \langle C_t,R_t,c_0,\ldots ,c_{n_t-1} \rangle $
. Clearly, d is uniformly computable from
![]() $\langle A,\Delta ,\Gamma \rangle $
.
$\langle A,\Delta ,\Gamma \rangle $
.
Now fix
![]() $t_0$
so that
$t_0$
so that
![]() $C_t = C$
,
$C_t = C$
,
![]() $R_t = R$
, and
$R_t = R$
, and
![]() $s_t = s$
for all
$s_t = s$
for all
![]() $t \geq t_0$
. Let
$t \geq t_0$
. Let
![]() $n = n_{t_0}$
, the number of leaves of R, and enumerate the leaves in lexicographic order as
$n = n_{t_0}$
, the number of leaves of R, and enumerate the leaves in lexicographic order as
![]() $\lambda _0,\ldots ,\lambda _{n-1}$
. For each
$\lambda _0,\ldots ,\lambda _{n-1}$
. For each
![]() $t \geq t_0$
and
$t \geq t_0$
and
![]() $i < n$
, the approximations
$i < n$
, the approximations
![]() $\langle V_{t,i,u} : u \in \omega \rangle $
to
$\langle V_{t,i,u} : u \in \omega \rangle $
to
![]() $W_{f,C_t,\lambda _i} = W_{f,C,\lambda _i}$
now only depend on i (and not t). Thus, we may fix
$W_{f,C_t,\lambda _i} = W_{f,C,\lambda _i}$
now only depend on i (and not t). Thus, we may fix
![]() $t_1 \geq t_0$
so that additionally, for every
$t_1 \geq t_0$
so that additionally, for every
![]() $i < n$
and every
$i < n$
and every
![]() $t \geq t_1$
, we have
$t \geq t_1$
, we have
![]() $V_{t,i,t} \supseteq W_{f,C,\lambda _i}$
. By construction of d, we have that if
$V_{t,i,t} \supseteq W_{f,C,\lambda _i}$
. By construction of d, we have that if
![]() $t \geq t_1$
then
$t \geq t_1$
then
![]() $d(t) = \langle C,R,c_0,\ldots ,c_{n-1} \rangle $
for some
$d(t) = \langle C,R,c_0,\ldots ,c_{n-1} \rangle $
for some
![]() $c_0,\ldots ,c_{n-1}$
with
$c_0,\ldots ,c_{n-1}$
with
![]() $c_i \in C \setminus V_{t,i,t}$
for each
$c_i \in C \setminus V_{t,i,t}$
for each
![]() $i < n$
. The value of each
$i < n$
. The value of each
![]() $c_i$
may depend on t, but since
$c_i$
may depend on t, but since
![]() $V_{t,i,t} \supseteq W_{f,C,\lambda _i}$
we have that
$V_{t,i,t} \supseteq W_{f,C,\lambda _i}$
we have that
![]() $c_i \in C \setminus W_{f,C,\lambda _i}$
. Hence, the range of d is bounded, so d is an instance of
$c_i \in C \setminus W_{f,C,\lambda _i}$
. Hence, the range of d is bounded, so d is an instance of
![]() $\mathsf {RT}^1_{\mathbb {N}}$
, as desired.
$\mathsf {RT}^1_{\mathbb {N}}$
, as desired.
Now consider any infinite homogeneous set
![]() $M \subseteq \omega $
for d. As noted above, the color of M under d must be
$M \subseteq \omega $
for d. As noted above, the color of M under d must be
![]() $\langle C,R,c_0,\ldots ,c_{n-1} \rangle $
, where
$\langle C,R,c_0,\ldots ,c_{n-1} \rangle $
, where
![]() $c_i \in C \setminus W_{f,C,\lambda _i}$
for each
$c_i \in C \setminus W_{f,C,\lambda _i}$
for each
![]() $i < n$
. By the choice of C and R, we can apply the A-computable procedure of Lemma 5.5 to find a
$i < n$
. By the choice of C and R, we can apply the A-computable procedure of Lemma 5.5 to find a
![]() $c \in \{ c_i : i < n \}$
and a finite set
$c \in \{ c_i : i < n \}$
and a finite set
![]() $S \trianglelefteq R$
of height
$S \trianglelefteq R$
of height
![]() $\mathrm {ht}(R)/|C|$
that is monochromatic for f with color c and such that
$\mathrm {ht}(R)/|C|$
that is monochromatic for f with color c and such that
![]() $c_i = c$
for every
$c_i = c$
for every
![]() $\lambda _i$
that extends a leaf of S, and
$\lambda _i$
that extends a leaf of S, and
![]() $\Gamma (A,S)(0) \downarrow $
.
$\Gamma (A,S)(0) \downarrow $
.
We now show that
![]() $\Gamma (A,S)(0)$
is a
$\Gamma (A,S)(0)$
is a
![]() ${}^1 \mathsf {TT}^1_{\mathbb {N}}$
-solution to
${}^1 \mathsf {TT}^1_{\mathbb {N}}$
-solution to
![]() $\langle A,\Delta ,\Gamma \rangle $
. Since
$\langle A,\Delta ,\Gamma \rangle $
. Since
![]() $c_i \in C \setminus W_{f,C,\lambda _i}$
for each
$c_i \in C \setminus W_{f,C,\lambda _i}$
for each
![]() $i < n$
, it follows by Lemma 5.2 (2) that the set
$i < n$
, it follows by Lemma 5.2 (2) that the set
![]() $\{ \rho \in 2^{<\omega } : f(\rho ) = c_i \}$
is dense above some extension of
$\{ \rho \in 2^{<\omega } : f(\rho ) = c_i \}$
is dense above some extension of
![]() $\lambda _i$
. In particular, this is true for the
$\lambda _i$
. In particular, this is true for the
![]() $\lambda _i$
extending the leaves of S, for which
$\lambda _i$
extending the leaves of S, for which
![]() $c_i = c$
. We can now argue as in the ending of the proof of Lemma 5.5 to conclude that there is an
$c_i = c$
. We can now argue as in the ending of the proof of Lemma 5.5 to conclude that there is an
![]() $H \cong 2^{<\omega }$
monochromatic for f with color c and such that
$H \cong 2^{<\omega }$
monochromatic for f with color c and such that
![]() $H^{\mathrm {rk} < \mathrm {ht}(R)/|C|} = S$
. Hence,
$H^{\mathrm {rk} < \mathrm {ht}(R)/|C|} = S$
. Hence,
![]() $\Gamma (A,H)(0)$
is a
$\Gamma (A,H)(0)$
is a
![]() ${}^1 \mathsf {TT}^1_{\mathbb {N}}$
-solution to
${}^1 \mathsf {TT}^1_{\mathbb {N}}$
-solution to
![]() $\langle A,\Delta ,\Gamma \rangle $
, and by our use conventions,
$\langle A,\Delta ,\Gamma \rangle $
, and by our use conventions,
![]() $\Gamma (A,H)(0) = \Gamma (A,H^{\mathrm {rk} < \mathrm {ht}(R)/|C|})(0) = \Gamma (A,S)(0)$
, as desired. This completes the proof.
$\Gamma (A,H)(0) = \Gamma (A,H^{\mathrm {rk} < \mathrm {ht}(R)/|C|})(0) = \Gamma (A,S)(0)$
, as desired. This completes the proof.
Corollary 5.8.
![]() ${}^1 \mathsf {TT}^1_{\mathbb {N}} \equiv _{\mathrm {W}} \mathsf {RT}^1_{\mathbb {N}}$
.
${}^1 \mathsf {TT}^1_{\mathbb {N}} \equiv _{\mathrm {W}} \mathsf {RT}^1_{\mathbb {N}}$
.
Since, trivially
![]() ${}^1 \mathsf {TT}^1_k \leq _{\mathrm {W}} \mathsf {TT}^1_{\mathbb {N}}$
for all
${}^1 \mathsf {TT}^1_k \leq _{\mathrm {W}} \mathsf {TT}^1_{\mathbb {N}}$
for all
![]() $k \geq 2$
, but
$k \geq 2$
, but
![]() $\mathsf {TT}^1_k \nleq _{\mathrm {W}} \mathsf {RT}^1_{\mathbb {N}}$
by Theorem 4.7, we immediately obtain the following.
$\mathsf {TT}^1_k \nleq _{\mathrm {W}} \mathsf {RT}^1_{\mathbb {N}}$
by Theorem 4.7, we immediately obtain the following.
Corollary 5.9. For every
![]() $j,k \geq 2$
,
$j,k \geq 2$
,
![]() $\mathsf {TT}^1_k \nleq _{\mathrm {W}} {}^1 \mathsf {TT}^1_j$
. In particular,
$\mathsf {TT}^1_k \nleq _{\mathrm {W}} {}^1 \mathsf {TT}^1_j$
. In particular,
![]() $\mathsf {TT}^1_k$
is not Weihrauch equivalent to any first-order problem.
$\mathsf {TT}^1_k$
is not Weihrauch equivalent to any first-order problem.
Thus we also have the analogue, in the Weihrauch degrees, of the remark made at the end of Section 1 that
![]() $\mathsf {TT}^1$
is not equivalent to any
$\mathsf {TT}^1$
is not equivalent to any
![]() $\Pi ^1_1$
statement over
$\Pi ^1_1$
statement over
![]() $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
.
6 Questions
We conclude with a few questions left over from our analysis, some concrete and some more open-ended. One line of inquiry concerns clarifying the relationship between the problems studied here and various weaker forms of the infinite pigeonhole principle. A notable example, ubiquitous in the literature, is closed choice on k-element sets,
![]() $\mathsf {C}_k$
(cf. [Reference Brattka, Gherardi and Pauly1, Section 7].) Recently, Pauly [Reference Pauly22] has shown that
$\mathsf {C}_k$
(cf. [Reference Brattka, Gherardi and Pauly1, Section 7].) Recently, Pauly [Reference Pauly22] has shown that
![]() $\mathsf {C}_3 \nleq _{\mathrm {W}} \mathsf {TT}^1_2$
. By results of Brattka and Rakotoniaina [Reference Brattka and Rakotoniaina2, Proposition 7.4] is known than
$\mathsf {C}_3 \nleq _{\mathrm {W}} \mathsf {TT}^1_2$
. By results of Brattka and Rakotoniaina [Reference Brattka and Rakotoniaina2, Proposition 7.4] is known than
![]() $\mathsf {C}_3 <_{\mathrm {W}} \mathsf {RT}^1_3$
and that
$\mathsf {C}_3 <_{\mathrm {W}} \mathsf {RT}^1_3$
and that
![]() $\mathsf {C}_3 \nleq _{\mathrm {W}} \mathsf {RT}^1_2$
. Pauly’s theorem therefore improves our Theorem 4.1 for
$\mathsf {C}_3 \nleq _{\mathrm {W}} \mathsf {RT}^1_2$
. Pauly’s theorem therefore improves our Theorem 4.1 for
![]() $k = 3$
and
$k = 3$
and
![]() $j = 2$
. Some other related results appear in recent work of Gill [Reference Gill14], but many basic questions remain open.
$j = 2$
. Some other related results appear in recent work of Gill [Reference Gill14], but many basic questions remain open.
In Corollary 5.8 we obtained an answer to the analog of the longstanding question, discussed in the introduction, of whether the first-order part of
![]() $\mathsf {TT}^1$
is
$\mathsf {TT}^1$
is
![]() $\mathsf {RT}^1$
. This relied on Theorem 5.7, and on the machinery of rakes used in its proof. This raises the following question.
$\mathsf {RT}^1$
. This relied on Theorem 5.7, and on the machinery of rakes used in its proof. This raises the following question.
Question 6.1. Can the combinatorics deployed in the proof of Theorem 5.7 be adapted and applied to study the strength of
![]() $\mathsf {TT}^1$
in second-order arithmetic?
$\mathsf {TT}^1$
in second-order arithmetic?
Recently, Chong, Li, Wang, and Yang [Reference Chong, Li, Wang and Yang4, Theorem 4.1] showed that
![]() $\mathsf {TT}^1$
is conservative over
$\mathsf {TT}^1$
is conservative over
![]() $\mathsf {RCA}_0 + \mathsf {RT}^1 + \mathsf {P}\Sigma ^0_1$
. Here,
$\mathsf {RCA}_0 + \mathsf {RT}^1 + \mathsf {P}\Sigma ^0_1$
. Here,
![]() $\mathsf {P}\Sigma ^0_1$
(cf. [Reference Chong, Li, Wang and Yang4, Definition 4.4]) is a certain arithmetical principle equivalent, by results of Kreuzer and Yokoyama [Reference Kreuzer and Yokoyama19, Theorem 1.3], to the totality of the Ackermann–Péter function relativized to any strictly monotonic function. Whether the first-order part of
$\mathsf {P}\Sigma ^0_1$
(cf. [Reference Chong, Li, Wang and Yang4, Definition 4.4]) is a certain arithmetical principle equivalent, by results of Kreuzer and Yokoyama [Reference Kreuzer and Yokoyama19, Theorem 1.3], to the totality of the Ackermann–Péter function relativized to any strictly monotonic function. Whether the first-order part of
![]() $\mathsf {TT}^1$
is
$\mathsf {TT}^1$
is
![]() $\mathsf {RT}^1$
is thus equivalent to whether
$\mathsf {RT}^1$
is thus equivalent to whether
![]() $\mathsf {P}\Sigma ^0_1$
can be eliminated in this result. In connection with Question 6.1, we can ask the following.
$\mathsf {P}\Sigma ^0_1$
can be eliminated in this result. In connection with Question 6.1, we can ask the following.
Question 6.2. Does
![]() $\mathsf {P}\Sigma ^0_1$
admit a natural form (or forms) as an instance-solution problem? How does it (or, do they) compare under Weihrauch reducibility with the various versions of
$\mathsf {P}\Sigma ^0_1$
admit a natural form (or forms) as an instance-solution problem? How does it (or, do they) compare under Weihrauch reducibility with the various versions of
![]() $\mathsf {TT}^1$
studied in this article?
$\mathsf {TT}^1$
studied in this article?
Lastly, we ask a general question, implicit in earlier papers like [Reference Dzhafarov, Solomon and Yokoyama13] and [Reference Soldà and Valenti26].
Question 6.3. What is the precise relationship between the first-order parts of problems in the context of Weihrauch reducibility, and the first-order parts of principles in the context of reverse mathematics?
Our results here add to the body of evidence showing that some sort of connection between the two notions exists. Whether Question 6.3 can be answered for a certain class of problems/principles, or whether the notion of first-order part under Weihrauch reducibility needs to be further refined to make some kind of answer possible, is unknown. In our view, clarifying this situation would yield important foundational insight, and further investigation is warranted.
Acknowledgments
The authors thank Leszek Kołodziejczyk, Ludovic Levy Patey, and Arno Pauly for valuable discussions at various stages of the writing of this article. They also thank the two anonymous referees for helpful comments and suggestions.
Funding
D.D.D. and D.R.S. were partially supported by a Focused Research Group grant from the National Science Foundation of the United States, DMS-1854355.