Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-25T22:00:09.463Z Has data issue: false hasContentIssue false
  • English
  • Français

A transfer principle in harmonic analysis1

Published online by Cambridge University Press:  12 March 2014

Gaisi Takeuti
Gaisi Takeuti*
Affiliation:
University of Illinois at Urbana-Champaign, Urbana, Illinois 61801
Get access Rights & Permissions [Opens in a new window]

Extract

Let G be a locally compact abelian group, Γ its dual group, and μ its Haar measure. For a function f: G → C, the Fourier transform 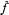of f is defined by

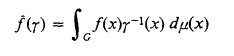
for every γ ∈ Γ.

We extend this definition for a function f on G, whose values are pairwise commutable normal operators in a Hilbert space. Then we study harmonic analysis for this extended Fourier transform.

Our method is Boolean valued analysis as introduced in [11] and [12]. Instead of developing the theory in a step-by-step manner, we shall develop a general machinery showing how to transform classical theorems to theorems in our situation.

In Chapter 1, we summarize the basic knowledge on Hilbert space, on Boolean valued model of set theory, and on Boolean valued analysis. In Chapter 2, we develop the theory of integration. Since we deal with unbounded operators as well as bounded operators, we need a new theory of integration. For a separable Hilbert space, the value of our integration coincides with the value of the usual integration with an adequate generalization for unbounded operators.

In Chapter 3, we establish machinery for our transfer principle and carry out the transformation of many classical theorems to theorems for our case.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 44 , Issue 3 , September 1979 , pp. 417 - 440
Copyright
Copyright © Association for Symbolic Logic 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

An article based on an invited address delivered to the Association for Symbolic Logic in Houston, Texas on April 7, 1978.

References

REFERENCES

[1]Bell, J. L., Boolean-valued models and independence proofs in set theory, Oxford University Press, London, 1978.Google Scholar
[2]Daniell, P., A general form of integral, Annals of Mathematics, vol. 19(1917), pp. 279–294.CrossRefGoogle Scholar
[3]Goldberg, R. R., Fourier transforms, Cambridge, 1970Google Scholar
[4]Halmos, P., Measure theory, Van Nostrand, New York, 1950.CrossRefGoogle Scholar
[5]Hille, E. and Phillips, R. S., Functional analysis and semi-groups, American Mathematical Society, Providence, RI, 1957.Google Scholar
[6]Loomis, L., An introduction to abstract harmonic analysis, Van Nostrand, New York, 1953.Google Scholar
[7]Nachbin, L., The Haar integral, Van Nostrand, New York, 1965.Google Scholar
[8]Rudin, W., Fourier analysis on groups. Interscience, New York, 1962.Google Scholar
[9]Solovay, R. M. and Tennenbaum, S., Iterated Cohen extensions and Souslin's problem, Annals of Mathematics, vol. 94(1971), pp. 201–245.CrossRefGoogle Scholar
[10]Stone, M. H., Note on integration, Proceedings of the National Academy of Sciences of the United States of America, I, II, III, vol. 34(1948), IV, vol. 35(1949).Google Scholar
[11]Takeuti, G., Two applications of logic to mathematics, Iwanami Shoten, Japan and Princeton University Press, Princeton, 1978.Google Scholar
[12]Takeuti, G., Boolean valued analysis, Proceedings of the 1977 Durham Research Symposium on Applications of Sheaf Theory to Logic, Algebra and Analysis, Lecture Notes in Mathematics, Springer-Verlag, Berlin and New York (to appear).Google Scholar
[13]Takeuti, G. and Zaring, W., Axiomatic set theory, Springer, New York, 1973.CrossRefGoogle Scholar
[14]Weil, A., L'intégration dans les groupes topologiques et ses applications, Gauthiers-Villars, Paris, 1938.Google Scholar