Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T19:33:22.006Z Has data issue: false hasContentIssue false
  • English
  • Français

Torre models in the isols

Published online by Cambridge University Press:  12 March 2014

Joseph Barback
Joseph Barback*
Affiliation:
Mathematics Department, State University of New York, College at Buffalo, Buffalo, New York 14222
Get access Rights & Permissions [Opens in a new window]

Abstract

In [14] J. Hirschfeld established the close connection of models of the true AE sentences of Peano Arithmetic and homomorphic images of the semiring of recursive functions. This fragment of Arithmetic includes most of the familiar results of classical number theory. There are two nice ways that such models appear in the isols. One way was introduced by A. Nerode in [20] and is referred to in the literature as Nerode Semirings. The other way is called a tame model. It is very similar to a Nerode Semiring and was introduced in [6]. The model theoretic properties of Nerode Semirings and tame models have been widely studied by T. G. McLaughlin ([16], [17], and [18]).

In this paper we introduce a new variety of tame model called a torre model. It has as a generator an infinite regressive isol with a nice structural property relative to recursively enumerable sets and their extensions to the isols. What is then obtained is a nonstandard model in the isols of the 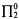fragment of Peano Arithmetic with the following property: Let T be a torre model. Let f be any recursive function, and let fΛ be its extension to the isols. If there is an isol A with fΛ(A) ϵ T, then there is also an isol B ϵ T with fΛ(B) = fΛ(A).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 59 , Issue 1 , March 1994 , pp. 140 - 150
Copyright
Copyright © Association for Symbolic Logic 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Barback, J., Recursive functions and regressive isols, Mathematica Scandinavica, vol. 15 (1964), pp. 29–42.CrossRefGoogle Scholar
[2]Barback, J., On recursive sets and regressive isols, Michigan Mathematical Journal, vol. 15 (1968), pp. 27–32.CrossRefGoogle Scholar
[3]Barback, J., Extensions to regressive isols, Mathematica Scandinavica, vol. 25 (1969), pp. 159–177.CrossRefGoogle Scholar
[4]Barback, J., On solutions in the regressive isols, Pacific Journal of Mathematics, vol. 43 (1972), pp. 283–296.CrossRefGoogle Scholar
[5]Barback, J., On tame regressive isols, Houston Journal of Mathematics, vol. 8 (1982), pp. 153–159.Google Scholar
[6]Barback, J., Tame models in the isols, Houston Journal of Mathematics, vol. 12 (1986), pp. 163–175.Google Scholar
[7]Barback, J., Corrections for two papers on tame regressive isols and tame models in the isols, Houston Journal of Mathematics, vol. 13 (1987), pp. 301–302.Google Scholar
[8]Barback, J., On the minimality of tame models in the isols, Proceedings of the American Mathematical Society (to appear).Google Scholar
[9]Barback, J. and Jackson, W. D., On representations as an infinite series of isols, Compositio Mathematica, vol. 22 (1970), pp. 347–365.Google Scholar
[10]Barback, J., On recursive functions and regressive isols, Pacific Journal of Mathematics, vol. 139 (1989), pp. 209–224.CrossRefGoogle Scholar
[11]Dekker, J. C. E. and Myhill, J., Recursive equivalence types, University of California Publications in Mathematics (N.S.), vol. 3 (1960), pp. 67–214.Google Scholar
[12]Ellentuck, E., Review of Extensions to isols, by A. Nerode, Mathematical Reviews, vol. 24 (1962), #A1215.Google Scholar
[13]Ellentuck, E., Diagonal methods in the theory of isols, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 26 (1980), pp. 193–204.CrossRefGoogle Scholar
[14]Hirschfeld, J., Models of arithmetic and recursive functions, Israel Journal of Mathematics, vol. 20 (1975), pp. 111–126.CrossRefGoogle Scholar
[15]McLaughlin, T. G., Regressive Sets and the Theory of Isols, Lecture Notes in Pure and Applied Mathematics, vol. 66, Marcel Dekker, New York, 1982.Google Scholar
[16]McLaughlin, T. G., Nerode semirings and Barback's ‘Tame Models’, Houston Journal of Mathematics, vol. 12 (1986), pp. 211–223.Google Scholar
[17]McLaughlin, T. G., Recursive fibers of RST isols, Proceedings of the American Mathematical Society, vol. 117 (1993), pp. 1141–1147.CrossRefGoogle Scholar
[18]McLaughlin, T. G., Characterizing existential completeness for Nerode Semirings, manuscript.Google Scholar
[19]Nerode, A., Extensions to isols, Annals of Mathematics, vol. 73 (1961), pp. 362–403.CrossRefGoogle Scholar
[20]McLaughlin, T. G., Diophantine correct nonstandard models in the isols, Annals of Mathematics, vol. 84 (1966), pp. 421–432.Google Scholar
[21]Skolem, T., Peano's axioms and models of arithmetic, Selected Works in Logic, (Fenstad, J. E., editor), Universitetsforlaget, Oslo, 1970, pp. 587–600.Google Scholar