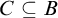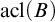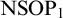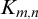1. Introduction
The basis for this paper is the discovery that a certain well-known property of dividing independence, which was originally stated in [Reference Adler3] and appears as folklore in a number of places, is actually false.
To elaborate, let T be a complete first-order theory with monster model
![]() $\mathbb M$
. We let
$\mathbb M$
. We let ![]() denote dividing independence for (small) sets in
denote dividing independence for (small) sets in
![]() $\mathbb M$
(see Definition 2.2). Given
$\mathbb M$
(see Definition 2.2). Given
![]() $C\subset \mathbb M$
, we say that
$C\subset \mathbb M$
, we say that ![]() has algebraic extension over C if, for any
has algebraic extension over C if, for any
![]() $A,B\subset \mathbb M$
,
$A,B\subset \mathbb M$
, ![]() implies
implies ![]() . We say that
. We say that ![]() has algebraic extension if this holds over any
has algebraic extension if this holds over any
![]() $C\subset \mathbb M$
.
$C\subset \mathbb M$
.
Remark 5.4(3) of [Reference Adler3] states that ![]() always has algebraic extension. This also appears as Exercise 1.24
always has algebraic extension. This also appears as Exercise 1.24
![]() $(iii)$
in Chapter 1 of Adler’s thesis [Reference Adler1] (later published as [Reference Adler3]). A solution to this exercise is given in [Reference Adler1]; however, a gap in the argument was found by the first-named author and Terry in February 2013. At that time, Adler suggested a new proof (via personal communication), which was rewritten in notes posted on the first-named author’s website. Then, in February of 2021, the second-named author found that the same gap was still present in the new proof, but hidden in a more subtle way, and subsequently discovered one of three counterexamples we will present here. Each of these examples demonstrates unique aspects of how and where algebraic extension for
$(iii)$
in Chapter 1 of Adler’s thesis [Reference Adler1] (later published as [Reference Adler3]). A solution to this exercise is given in [Reference Adler1]; however, a gap in the argument was found by the first-named author and Terry in February 2013. At that time, Adler suggested a new proof (via personal communication), which was rewritten in notes posted on the first-named author’s website. Then, in February of 2021, the second-named author found that the same gap was still present in the new proof, but hidden in a more subtle way, and subsequently discovered one of three counterexamples we will present here. Each of these examples demonstrates unique aspects of how and where algebraic extension for ![]() can fail. To help provide context for how these examples have been curated, note that
can fail. To help provide context for how these examples have been curated, note that ![]() does have algebraic extension over C whenever forking and dividing over C are the same for complete types (see Remark 2.11). So, for example,
does have algebraic extension over C whenever forking and dividing over C are the same for complete types (see Remark 2.11). So, for example, ![]() has algebraic extension in any simple theory. More generally, if T is
has algebraic extension in any simple theory. More generally, if T is
![]() $\mathrm {NTP}_2$
and C is an extension base for nonforking, then
$\mathrm {NTP}_2$
and C is an extension base for nonforking, then ![]() has algebraic extension over C by [Reference Chernikov and Kaplan6]. With these facts in mind, we now give an overview of our examples.
has algebraic extension over C by [Reference Chernikov and Kaplan6]. With these facts in mind, we now give an overview of our examples.
-
(1) In Section 3.1, we show that
 fails algebraic extension over
fails algebraic extension over
 $\varnothing $
in
$\varnothing $
in
 $T=\mathrm {Th}({\mathbb Q},\operatorname {cyc})^{\mathrm {eq}}$
where
$T=\mathrm {Th}({\mathbb Q},\operatorname {cyc})^{\mathrm {eq}}$
where
 $\operatorname {cyc}$
is the circular order on
$\operatorname {cyc}$
is the circular order on
 ${\mathbb Q}$
. Note that T is NIP, and that
${\mathbb Q}$
. Note that T is NIP, and that
 $\varnothing $
is (necessarily) not an extension base for nonforking in T.
$\varnothing $
is (necessarily) not an extension base for nonforking in T. -
(2) In Section 3.2, we show that
 fails algebraic extension over a model in the
fails algebraic extension over a model in the
 $\mathrm {NSOP}_1$
theory
$\mathrm {NSOP}_1$
theory
 $T=(T^{\varnothing }_{f})^{\mathrm {eq}}$
, where
$T=(T^{\varnothing }_{f})^{\mathrm {eq}}$
, where
 $T^{\varnothing }_{f}$
is the model completion of the empty theory in a language with only a binary function symbol f. In this case, the failure of algebraic extension for
$T^{\varnothing }_{f}$
is the model completion of the empty theory in a language with only a binary function symbol f. In this case, the failure of algebraic extension for  actually arises through the failure of
actually arises through the failure of  (see Section 2.3 for further discussion of M-independence). Thus this example also refutes the claim made in Remark 5.4(4) of [Reference Adler3]. We also show that in T, all sets are extension bases for nonforking.
(see Section 2.3 for further discussion of M-independence). Thus this example also refutes the claim made in Remark 5.4(4) of [Reference Adler3]. We also show that in T, all sets are extension bases for nonforking. -
(3) In Section 3.3, we construct a theory, called
 $T_{\mathsf {OG}}$
, where
$T_{\mathsf {OG}}$
, where  fails algebraic extension for the stronger reason that
fails algebraic extension for the stronger reason that  need not imply
need not imply  (see Remark 2.9 for further discussion).
(see Remark 2.9 for further discussion).
 $T_{\mathsf {OG}}$
is an
$T_{\mathsf {OG}}$
is an
 $\mathrm {NSOP}_4$
theory (with
$\mathrm {NSOP}_4$
theory (with
 $\mathrm {SOP}_3$
) in which all sets are extension bases for nonforking. This is the original counterexample discovered by the second-named author.
$\mathrm {SOP}_3$
) in which all sets are extension bases for nonforking. This is the original counterexample discovered by the second-named author.
In addition to refuting the erroneous claims made in [Reference Adler3, Remark 5.4], these counterexamples also answer some other open questions. First, recall that if ![]() (i.e., forking and dividing coincide for complete types), then all sets are extension bases for nonforking. Question A.1 of Adler’s thesis [Reference Adler1] asks whether the converse holds. As noted above, if
(i.e., forking and dividing coincide for complete types), then all sets are extension bases for nonforking. Question A.1 of Adler’s thesis [Reference Adler1] asks whether the converse holds. As noted above, if ![]() fails algebraic extension, then
fails algebraic extension, then ![]() , and thus both
, and thus both
![]() $(2)$
and
$(2)$
and
![]() $(3)$
provide counterexamples to Adler’s question. Moreover,
$(3)$
provide counterexamples to Adler’s question. Moreover,
![]() $(2)$
and
$(2)$
and
![]() $(3)$
appear to be the first known examples of
$(3)$
appear to be the first known examples of
![]() $\mathrm {NSOP}$
theories in which
$\mathrm {NSOP}$
theories in which ![]() . Whether
. Whether ![]() in
in
![]() $\mathrm {NSOP}_1$
theories specifically had been discussed by a number of people in the field, and was asked by d’Elbée in [Reference d’Elbée12, Question 2]. Example
$\mathrm {NSOP}_1$
theories specifically had been discussed by a number of people in the field, and was asked by d’Elbée in [Reference d’Elbée12, Question 2]. Example
![]() $(2)$
shows that
$(2)$
shows that ![]() need not hold in
need not hold in
![]() $\mathrm {NSOP}_1$
theories, even over models. In fact, since the discovery of this example, two others have surfaced in previous literature from erroneous arguments relying on [Reference Adler3, Remark 5.4] (see Sections 5.3 and 5.4).
$\mathrm {NSOP}_1$
theories, even over models. In fact, since the discovery of this example, two others have surfaced in previous literature from erroneous arguments relying on [Reference Adler3, Remark 5.4] (see Sections 5.3 and 5.4).
We now give an outline of the paper. In Section 2 we recall various definitions, and then we spend some time discussing positive results related to [Reference Adler3, Remark 5.4] that are still true. For example, algebraic extension can be viewed as one part of the more general question of preservation of algebraic closure for a ternary relation (Definition 2.5). We clarify in Proposition 2.7 what amount of preservation one can obtain for ![]() , and we show that
, and we show that ![]() always preserves algebraic closure. These facts are known in the folklore, but for obvious reasons we think it appropriate to provide details. Then in Section 2.3 we focus on the question of when
always preserves algebraic closure. These facts are known in the folklore, but for obvious reasons we think it appropriate to provide details. Then in Section 2.3 we focus on the question of when ![]() implies
implies ![]() , which was the main motivation for [Reference Adler3, Remark 5.4]. Among other quick observations, we show in Proposition 2.18 that
, which was the main motivation for [Reference Adler3, Remark 5.4]. Among other quick observations, we show in Proposition 2.18 that ![]() implies
implies ![]() in pregeometric theories (where
in pregeometric theories (where ![]() is especially meaningful; see Fact 2.17). We then move on to our three counterexamples summarized above, which are given in Section 3. The rest of the paper is devoted to addressing uses of [Reference Adler3, Remark 5.4] in previous literature. First, in Section 4, we focus on free amalgamation theories, defined by the first-named author in [Reference Conant7]. It turns out that the theory
is especially meaningful; see Fact 2.17). We then move on to our three counterexamples summarized above, which are given in Section 3. The rest of the paper is devoted to addressing uses of [Reference Adler3, Remark 5.4] in previous literature. First, in Section 4, we focus on free amalgamation theories, defined by the first-named author in [Reference Conant7]. It turns out that the theory
![]() $T_{\mathsf {OG}}$
in example
$T_{\mathsf {OG}}$
in example
![]() $(3)$
above is a free amalgamation theory with disintegrated algebraic closure (Corollary 4.9). Consequently, the failure of algebraic extension in
$(3)$
above is a free amalgamation theory with disintegrated algebraic closure (Corollary 4.9). Consequently, the failure of algebraic extension in
![]() $T_{\mathsf {OG}}$
refutes the claim made in an earlier unpublished research note (of the authors) that
$T_{\mathsf {OG}}$
refutes the claim made in an earlier unpublished research note (of the authors) that ![]() in any such theory. However, the arguments from that note can be adjusted to show that forking and dividing are the same for complete types over algebraically closed sets (see Theorem 4.5). Finally, Section 5 contains brief discussion of other places where [Reference Adler3, Remark 5.4] was used. For example, we amend some incorrect statements from [Reference Conant and Kruckman10] about dividing in the generic theory of
in any such theory. However, the arguments from that note can be adjusted to show that forking and dividing are the same for complete types over algebraically closed sets (see Theorem 4.5). Finally, Section 5 contains brief discussion of other places where [Reference Adler3, Remark 5.4] was used. For example, we amend some incorrect statements from [Reference Conant and Kruckman10] about dividing in the generic theory of
![]() $K_{m,n}$
-free incidence structures.
$K_{m,n}$
-free incidence structures.
2. Dividing and algebraic closure
Throughout this section, we work in the setting of a complete theory T with monster model
![]() $\mathbb M$
. We allow letters
$\mathbb M$
. We allow letters
![]() $a,b,c,\ldots $
to denote tuples from
$a,b,c,\ldots $
to denote tuples from
![]() $\mathbb M$
(which may be infinite), but sometimes also use vector notation
$\mathbb M$
(which may be infinite), but sometimes also use vector notation
![]() $\overline {a},\overline {b},\overline {c},\ldots $
when the distinction between tuples and singletons is important.
$\overline {a},\overline {b},\overline {c},\ldots $
when the distinction between tuples and singletons is important.
2.1. Preliminaries
We first recall several axioms of a ternary relation ![]() on small subsets of
on small subsets of
![]() $\mathbb M$
.
$\mathbb M$
.
Definition 2.1.
-
(1) (Invariance) For all
 $A,B,C$
, if
$A,B,C$
, if  then
then  for all
for all
 $\sigma \in \operatorname {Aut}(\mathbb M)$
.
$\sigma \in \operatorname {Aut}(\mathbb M)$
. -
(2) (Monotonicity) For all
 $A,B,C$
, if
$A,B,C$
, if  then
then  for all
for all
 $A'\subseteq A$
and
$A'\subseteq A$
and
 $B'\subseteq B$
.
$B'\subseteq B$
. -
(3) (Base monotonicity) For all
 $A,B,C$
, if
$A,B,C$
, if  and
and
 $D\subseteq B$
then
$D\subseteq B$
then  .
. -
(4) (Extension) For all
 $A,B,C$
, if
$A,B,C$
, if  and
and
 $D\supseteq B$
, then there is some
$D\supseteq B$
, then there is some
 $A'\equiv _{BC} A$
such that
$A'\equiv _{BC} A$
such that  .
. -
(5) (Existence)
 for all A and C.
for all A and C.
Next we recall a few special independence relations.
Definition 2.2. Fix
![]() $A,B,C\subset \mathbb M$
, and let a be a tuple enumerating A.
$A,B,C\subset \mathbb M$
, and let a be a tuple enumerating A.
-
(1)
 if
if
 $\operatorname {tp}(a/BC)$
does not divide over C.
$\operatorname {tp}(a/BC)$
does not divide over C. -
(2)
 if
if
 $\operatorname {tp}(a/BC)$
does not fork over C.
$\operatorname {tp}(a/BC)$
does not fork over C. -
(3)
 if
if
 $\operatorname {acl}(AC)\cap \operatorname {acl}(BC)=\operatorname {acl}(C)$
.
$\operatorname {acl}(AC)\cap \operatorname {acl}(BC)=\operatorname {acl}(C)$
. -
(4)
 if
if
 $\operatorname {acl}(AD)\cap \operatorname {acl}(BD)=\operatorname {acl}(D)$
for any D such that
$\operatorname {acl}(AD)\cap \operatorname {acl}(BD)=\operatorname {acl}(D)$
for any D such that
 $C\subseteq D\subseteq \operatorname {acl}(BC)$
.
$C\subseteq D\subseteq \operatorname {acl}(BC)$
.
For complete definitions of forking and dividing, see [Reference Adler3] or [Reference Tent and Ziegler24, Chapter 7]. Recall also that a set
![]() $C\subset \mathbb M$
is called an extension base for nonforking if
$C\subset \mathbb M$
is called an extension base for nonforking if ![]() for any
for any
![]() $A\subset \mathbb M$
. Thus
$A\subset \mathbb M$
. Thus ![]() satisfies existence if and only if all sets are extension bases for nonforking.
satisfies existence if and only if all sets are extension bases for nonforking.
Remark 2.3. In Adler’s thesis [Reference Adler1], “existence” is used for a stronger axiom that is later renamed “full existence” in [Reference Adler3]. So to forestall potential confusion, we note that existence and full existence are equivalent for ![]() (see also [Reference Conant and Hanson9, Fact 4.2]).
(see also [Reference Conant and Hanson9, Fact 4.2]).
2.2. Algebraic extension and preservation of algebraic closure
The next definition repeats the key notion from the introduction, but in the the setting of a general ternary relation ![]() on small subsets of
on small subsets of
![]() $\mathbb M$
.
$\mathbb M$
.
Definition 2.4. A ternary relation ![]() has algebraic extension over
has algebraic extension over
![]() $C\subset \mathbb M$
if, for any
$C\subset \mathbb M$
if, for any
![]() $A,B\subset \mathbb M$
,
$A,B\subset \mathbb M$
, ![]() implies
implies ![]() . We say
. We say ![]() has algebraic extension if this holds over any
has algebraic extension if this holds over any
![]() $C\subset \mathbb M$
.
$C\subset \mathbb M$
.
We note that algebraic extension is nearly the same as the right closure axiom defined by d’Elbée in [Reference d’Elbée12, Reference d’Elbée13]. Indeed, the two are equivalent for ternary relations satisfying right monotonicity and right normality (![]() implies
implies ![]() ). These axioms are also related to the following stronger property.
). These axioms are also related to the following stronger property.
Definition 2.5. A ternary relation ![]() preserves algebraic closure if, for any
preserves algebraic closure if, for any
![]() $A,B,C\subset \mathbb M$
,
$A,B,C\subset \mathbb M$
,
Lemma 2.6. Let ![]() be an invariant ternary relation satisfying monotonicity and base monotonicity. Then
be an invariant ternary relation satisfying monotonicity and base monotonicity. Then ![]() preserves algebraic closure if and only if it has algebraic extension and satisfies the following axioms.
preserves algebraic closure if and only if it has algebraic extension and satisfies the following axioms.
-
(i) For any
 $A,B,C\subset \mathbb M$
, if
$A,B,C\subset \mathbb M$
, if  then
then  .
. -
(ii) For any
 $A,B,C\subset \mathbb M$
, if
$A,B,C\subset \mathbb M$
, if  then
then  .
.
Proof We only need to prove the nontrivial direction. Assume ![]() has algebraic extension and satisfies
has algebraic extension and satisfies
![]() $(i)$
and
$(i)$
and
![]() $(ii)$
. Then in order to establish preservation of algebraic closure for
$(ii)$
. Then in order to establish preservation of algebraic closure for ![]() , it suffices to prove:
, it suffices to prove:
-
(iii) For any
 $A,B,C\subset \mathbb M$
, if
$A,B,C\subset \mathbb M$
, if  then
then  .
. -
(iv) For any
 $A,B,C\subset \mathbb M$
, if
$A,B,C\subset \mathbb M$
, if  then
then  .
.
Both of these are immediate from monotonicity and base monotonicity for ![]() .
.
The reason we have not given axioms
![]() $(i)$
and
$(i)$
and
![]() $(ii)$
their own names is because our focus is on
$(ii)$
their own names is because our focus is on ![]() which, as we observe next, always satisfies these axioms.
which, as we observe next, always satisfies these axioms.
Proposition 2.7. In any theory, ![]() satisfies axioms
satisfies axioms
![]() $(i)$
and
$(i)$
and
![]() $(ii)$
of Lemma 2.6. Hence
$(ii)$
of Lemma 2.6. Hence ![]() preserves algebraic closure if and only if it has algebraic extension.
preserves algebraic closure if and only if it has algebraic extension.
Proof The second claim follows from the first by Lemma 2.6 and the fact that ![]() satisfies monotonicity and base monotonicity. So it remains to show
satisfies monotonicity and base monotonicity. So it remains to show ![]() satisfies
satisfies
![]() $(i)$
and
$(i)$
and
![]() $(ii)$
of Lemma 2.6.
$(ii)$
of Lemma 2.6.
For axiom
![]() $(i)$
, recall from [Reference Tent and Ziegler24, Corollary 7.1.5] that
$(i)$
, recall from [Reference Tent and Ziegler24, Corollary 7.1.5] that ![]() if and only if for any C-indiscernible sequence
if and only if for any C-indiscernible sequence
![]() $(b)_{i<\omega }$
, with
$(b)_{i<\omega }$
, with
![]() $b_0$
enumerating B, there is an
$b_0$
enumerating B, there is an
![]() $AC$
-indiscernible sequence
$AC$
-indiscernible sequence
![]() $(b^{\prime }_i)_{i<\omega }$
with the same type over
$(b^{\prime }_i)_{i<\omega }$
with the same type over
![]() $BC$
as
$BC$
as
![]() $(b_i)_{i<\omega }$
. Since any
$(b_i)_{i<\omega }$
. Since any
![]() $AC$
-indiscernible sequence is automatically
$AC$
-indiscernible sequence is automatically
![]() $\operatorname {acl}(AC)$
-indiscernible (see, e.g., [Reference Tent and Ziegler24, Exercise 7.1.1]), axiom
$\operatorname {acl}(AC)$
-indiscernible (see, e.g., [Reference Tent and Ziegler24, Exercise 7.1.1]), axiom
![]() $(i)$
follows.
$(i)$
follows.
For axiom
![]() $(ii)$
, assume
$(ii)$
, assume ![]() and let a and b be enumerations of A and B, respectively. Suppose
and let a and b be enumerations of A and B, respectively. Suppose
![]() $(b_i)_{i<\omega }$
is a C-indiscernible sequence with
$(b_i)_{i<\omega }$
is a C-indiscernible sequence with
![]() $b_0=b$
. Then
$b_0=b$
. Then
![]() $(b_i)_{i<\omega }$
is
$(b_i)_{i<\omega }$
is
![]() $\operatorname {acl}(C)$
-indiscernible. Since
$\operatorname {acl}(C)$
-indiscernible. Since ![]() , there is some
, there is some
![]() $a'$
such that
$a'$
such that
![]() $a'b_i\equiv _{\operatorname {acl}(C)}ab$
for all
$a'b_i\equiv _{\operatorname {acl}(C)}ab$
for all
![]() $i<\omega $
. Therefore
$i<\omega $
. Therefore
![]() $a'b_i\equiv _{C}ab$
for all
$a'b_i\equiv _{C}ab$
for all
![]() $i<\omega $
. Thus we have shown
$i<\omega $
. Thus we have shown ![]() .
.
Remark 2.8. It also follows that ![]() preserves algebraic closure if and only if, for all
preserves algebraic closure if and only if, for all
![]() $A,B,C\subset \mathbb M$
, we have
$A,B,C\subset \mathbb M$
, we have
Indeed, assume the latter condition holds. We show ![]() has algebraic extension, and hence preserves algebraic closure by Proposition 2.7. Suppose
has algebraic extension, and hence preserves algebraic closure by Proposition 2.7. Suppose ![]() . By assumption
. By assumption ![]() . Then
. Then ![]() by monotonicity, and thus
by monotonicity, and thus ![]() by Proposition 2.7.
by Proposition 2.7.
Remark 2.9. Suppose ![]() is an invariant ternary relation with monotonicity and base monotonicity (e.g.,
is an invariant ternary relation with monotonicity and base monotonicity (e.g., ![]() ). Consider the following axiom:
). Consider the following axiom:
Then clearly
![]() $(\dagger )$
holds if
$(\dagger )$
holds if ![]() has algebraic extension. So given that
has algebraic extension. So given that ![]() need not always satisfy algebraic extension, it becomes natural to ask whether the weaker axiom
need not always satisfy algebraic extension, it becomes natural to ask whether the weaker axiom
![]() $(\dagger )$
holds for
$(\dagger )$
holds for ![]() . The theory constructed in Section 3.3 will show that this is not always the case. It is also worth noting that for
. The theory constructed in Section 3.3 will show that this is not always the case. It is also worth noting that for ![]() specifically,
specifically,
![]() $(\dagger )$
is equivalent to the following weakening of algebraic extension:
$(\dagger )$
is equivalent to the following weakening of algebraic extension: ![]() .
.
Remark 2.10. Given
![]() $A,C\subset \mathbb M$
, we always have
$A,C\subset \mathbb M$
, we always have ![]() (since any C-indiscernible sequence is
(since any C-indiscernible sequence is
![]() $\operatorname {acl}(C)$
-indiscernible). Thus, any failure of algebraic extension over C for
$\operatorname {acl}(C)$
-indiscernible). Thus, any failure of algebraic extension over C for ![]() must involve a set B not contained in
must involve a set B not contained in
![]() $\operatorname {acl}(C)$
.
$\operatorname {acl}(C)$
.
Remark 2.11. In [Reference Adler3], algebraic extension is referred to as a “weak extension property” since it holds of any invariant ternary relation satisfying extension. Indeed, if ![]() satisfies extension and
satisfies extension and ![]() , then there is some
, then there is some
![]() $A'\equiv _{BC} A$
such that
$A'\equiv _{BC} A$
such that ![]() , whence
, whence ![]() by invariance.
by invariance.
Recall (e.g., from [Reference Adler3, Section 4]) that forking independence ![]() is obtained by “forcing the extension axiom” on
is obtained by “forcing the extension axiom” on ![]() . So in light of Proposition 2.7 and Remark 2.11, it is reasonable to expect
. So in light of Proposition 2.7 and Remark 2.11, it is reasonable to expect ![]() to preserve algebraic closure in any theory. This is again a folklore result (which is actually true in this case), however a proof does not seem to appear in the literature (it is stated for simple theories in [Reference Casanovas4, Proposition 5.20]). So we take the opportunity to provide details.
to preserve algebraic closure in any theory. This is again a folklore result (which is actually true in this case), however a proof does not seem to appear in the literature (it is stated for simple theories in [Reference Casanovas4, Proposition 5.20]). So we take the opportunity to provide details.
Proposition 2.12. In any theory, ![]() preserves algebraic closure.
preserves algebraic closure.
Proof Recall that ![]() satisfies monotonicity, base monotonicity, and extension (hence algebraic extension by Remark 2.11). So it suffices to show that
satisfies monotonicity, base monotonicity, and extension (hence algebraic extension by Remark 2.11). So it suffices to show that ![]() satisfies axioms
satisfies axioms
![]() $(i)$
and
$(i)$
and
![]() $(ii)$
of Lemma 2.6.
$(ii)$
of Lemma 2.6.
For axiom
![]() $(i)$
, suppose
$(i)$
, suppose ![]() . In order to show
. In order to show ![]() , we need to fix
, we need to fix
![]() $D\supseteq B$
and find
$D\supseteq B$
and find
![]() $E\equiv _{BC} \operatorname {acl}(AC)$
such that
$E\equiv _{BC} \operatorname {acl}(AC)$
such that ![]() . Since
. Since ![]() , there is
, there is
![]() $A'\equiv _{BC} A$
such that
$A'\equiv _{BC} A$
such that ![]() . So
. So ![]() by Proposition 2.7. Thus we can take
by Proposition 2.7. Thus we can take
![]() $E=\operatorname {acl}(A'C)$
.
$E=\operatorname {acl}(A'C)$
.
For axiom
![]() $(ii)$
, suppose
$(ii)$
, suppose ![]() . In order to show
. In order to show ![]() , we need to fix
, we need to fix
![]() $D\supseteq B$
and find
$D\supseteq B$
and find
![]() $A'\equiv _{BC} A$
such that
$A'\equiv _{BC} A$
such that ![]() . Since
. Since ![]() , there is
, there is
![]() $A'\equiv _{B\operatorname {acl}(C)} A$
such that
$A'\equiv _{B\operatorname {acl}(C)} A$
such that ![]() . Then
. Then
![]() $A'\equiv _{BC}A$
, and
$A'\equiv _{BC}A$
, and ![]() by Proposition 2.7.
by Proposition 2.7.
Corollary 2.13. If forking and dividing are the same for complete types (e.g., if T is simple), then ![]() preserves algebraic closure.
preserves algebraic closure.
2.3. M-independence
We now turn our focus to the relationship between dividing independence and M-independence. In [Reference Adler3], Adler uses the erroneous Remark 5.4(3) to conclude Remark 5.4(4), which says that ![]() implies
implies ![]() in any theory. The theory constructed in Section 3.2 will in fact also serve as a counterexample to [Reference Adler3, Remark 5.4(4)] (see Corollary 3.3). However, we should note that Adler’s primary motivation for the entirety of [Reference Adler3, Remark 5.4] is to obtain
in any theory. The theory constructed in Section 3.2 will in fact also serve as a counterexample to [Reference Adler3, Remark 5.4(4)] (see Corollary 3.3). However, we should note that Adler’s primary motivation for the entirety of [Reference Adler3, Remark 5.4] is to obtain ![]() . This implication, which is the more important one for the purposes of developing thorn-forking, is still true, since
. This implication, which is the more important one for the purposes of developing thorn-forking, is still true, since ![]() satisfies extension.
satisfies extension.
Remark 2.14. Although the implication ![]() does not hold in general, the weaker implication
does not hold in general, the weaker implication ![]() is always true. However, proofs of this fact in the literature often quote [Reference Adler3, Remark 5.4(3)]. This is further discussed in [Reference Conant and Hanson9, Section 2], where a direct proof of
is always true. However, proofs of this fact in the literature often quote [Reference Adler3, Remark 5.4(3)]. This is further discussed in [Reference Conant and Hanson9, Section 2], where a direct proof of ![]() is given using P. M. Neumann’s Lemma (see [Reference Conant and Hanson9, Proposition 2.3]; the argument is similar to a Mathematics Stack Exchange post of the second-named author [Reference Kruckman18]). As noted in [Reference Conant and Hanson9, Remark 4.12], there is another quick proof of
is given using P. M. Neumann’s Lemma (see [Reference Conant and Hanson9, Proposition 2.3]; the argument is similar to a Mathematics Stack Exchange post of the second-named author [Reference Kruckman18]). As noted in [Reference Conant and Hanson9, Remark 4.12], there is another quick proof of ![]() using extension for
using extension for ![]() . This argument is similar to another Mathematics Stack Exchange post of the second-named author [Reference Kruckman19], and we copy it here for completeness.
. This argument is similar to another Mathematics Stack Exchange post of the second-named author [Reference Kruckman19], and we copy it here for completeness.
Assume ![]() , and let a and b enumerate A and B. By extension for
, and let a and b enumerate A and B. By extension for ![]() and Erdős–Rado, one can construct a C-indiscernible sequence
and Erdős–Rado, one can construct a C-indiscernible sequence
![]() $(b_i)_{i<\omega }$
such that
$(b_i)_{i<\omega }$
such that
![]() $b_0=b$
and
$b_0=b$
and ![]() for all
for all
![]() $i<\omega $
. By [Reference Tent and Ziegler24, Corollary 7.1.5] (and [Reference Tent and Ziegler24, Exercise 7.1.1]), there is an
$i<\omega $
. By [Reference Tent and Ziegler24, Corollary 7.1.5] (and [Reference Tent and Ziegler24, Exercise 7.1.1]), there is an
![]() $\operatorname {acl}(a C)$
-indiscernible sequence
$\operatorname {acl}(a C)$
-indiscernible sequence
![]() $(b^{\prime }_i)_{i<\omega }$
such that
$(b^{\prime }_i)_{i<\omega }$
such that
![]() $(b^{\prime }_i)_{i<\omega }\equiv _{b_0 C}(b_i)_{i<\omega }$
. Therefore
$(b^{\prime }_i)_{i<\omega }\equiv _{b_0 C}(b_i)_{i<\omega }$
. Therefore

So ![]() , as desired.
, as desired.
A direct proof of extension for ![]() is given by Adler in [Reference Adler3, Proposition 1.5(1)]. A shorter proof using P. M. Neumann’s Lemma can be found in [Reference Conant and Hanson9, Proposition 2.1]. (Both [Reference Adler3] and [Reference Conant and Hanson9] actually focus on “full existence” for
is given by Adler in [Reference Adler3, Proposition 1.5(1)]. A shorter proof using P. M. Neumann’s Lemma can be found in [Reference Conant and Hanson9, Proposition 2.1]. (Both [Reference Adler3] and [Reference Conant and Hanson9] actually focus on “full existence” for ![]() ; see [Reference Conant and Hanson9, Fact 4.2].)
; see [Reference Conant and Hanson9, Fact 4.2].)
Remark 2.15. Recall that ![]() is often viewed as the result of “forcing base monotonicity” on
is often viewed as the result of “forcing base monotonicity” on ![]() . We can now see that this is slightly misleading. In particular, it would be desirable for the ternary relation obtained by forcing base monotonicity on
. We can now see that this is slightly misleading. In particular, it would be desirable for the ternary relation obtained by forcing base monotonicity on ![]() to be weaker than any other relation that has base monotonicity and implies
to be weaker than any other relation that has base monotonicity and implies ![]() . But this is not the case for
. But this is not the case for ![]() , since it is not always weaker than
, since it is not always weaker than ![]() (see Section 3.2). On the other hand, in [Reference Adler3, Corollary 4.8], Adler refers to a variation of M-independence, which is defined as
(see Section 3.2). On the other hand, in [Reference Adler3, Corollary 4.8], Adler refers to a variation of M-independence, which is defined as ![]() if and only if
if and only if ![]() for all
for all
![]() $C\subseteq D\subseteq BC$
. By definition,
$C\subseteq D\subseteq BC$
. By definition, ![]() has base monotonicity, implies
has base monotonicity, implies ![]() , and is weaker than any other relation with those properties (so, e.g.,
, and is weaker than any other relation with those properties (so, e.g., ![]() always holds). Altogether,
always holds). Altogether, ![]() is really the result of first forcing base monotonicity on
is really the result of first forcing base monotonicity on ![]() to obtain
to obtain ![]() , and then forcing algebraic extension on
, and then forcing algebraic extension on ![]() .
.
We will now examine some special cases in which one can recover the implication from ![]() to
to ![]() .
.
Remark 2.16.
-
(1) If
 has algebraic extension over
has algebraic extension over
 $C\subset \mathbb M$
then
$C\subset \mathbb M$
then  .
. -
(2) It is straightforward to show that
 always preserves definable closure. Thus if algebraic closure coincides with definable closure, then
always preserves definable closure. Thus if algebraic closure coincides with definable closure, then  has algebraic extension and hence
has algebraic extension and hence  .
. -
(3) If algebraic closure in T is modular then
 since, in this case,
since, in this case,  coincides with
coincides with  (see [Reference Adler3, Proposition 1.3
(see [Reference Adler3, Proposition 1.3
 $(3)$
]). However, the example in Section 3.3 has disintegrated algebraic closure. So it is not the case that if algebraic closure in T is modular then
$(3)$
]). However, the example in Section 3.3 has disintegrated algebraic closure. So it is not the case that if algebraic closure in T is modular then  has algebraic extension.
has algebraic extension.
Recall that a theory T is pregeometric if algebraic closure in T satisfies the exchange property. In this case, given a tuple
![]() $\overline {a}$
from
$\overline {a}$
from
![]() $\mathbb M$
and a set
$\mathbb M$
and a set
![]() $C\subset \mathbb M$
, we let
$C\subset \mathbb M$
, we let
![]() $\dim (\overline {a}/C)$
denote the size of an
$\dim (\overline {a}/C)$
denote the size of an
![]() $\operatorname {acl}$
-basis for
$\operatorname {acl}$
-basis for
![]() $\overline {a}$
over C. In pregeometric theories, M-independence is especially meaningful due to the following characterization.
$\overline {a}$
over C. In pregeometric theories, M-independence is especially meaningful due to the following characterization.
Fact 2.17. Suppose T is pregeometric. Then given
![]() $A,B,C\subset \mathbb M$
,
$A,B,C\subset \mathbb M$
, ![]() if and only if
if and only if
![]() $\dim (\overline {a}/BC)=\dim (\overline {a}/C)$
for any finite tuple
$\dim (\overline {a}/BC)=\dim (\overline {a}/C)$
for any finite tuple
![]() $\overline {a}$
from A. Moreover,
$\overline {a}$
from A. Moreover, ![]() is a strict independence relation in the sense of [Reference Adler3].
is a strict independence relation in the sense of [Reference Adler3].
As far as we are aware, an explicit statement and proof of Fact 2.17 first appeared in unpublished notes by Adler [Reference Adler2] (see also Theorems 1.2.12 and 1.2.15 of [Reference d’Elbée13]).
Proposition 2.18. If T is pregeometric then ![]() implies
implies ![]() .
.
Proof Assume T is pregeometric. Fix
![]() $A,B,C\subset \mathbb M$
such that
$A,B,C\subset \mathbb M$
such that ![]() . Then there is some set D such that
. Then there is some set D such that
![]() $C\subseteq D\subseteq \operatorname {acl}(BC)$
and
$C\subseteq D\subseteq \operatorname {acl}(BC)$
and ![]() . So there is some singleton
. So there is some singleton
![]() $e\in (\operatorname {acl}(AD)\cap \operatorname {acl}(BD))\backslash \operatorname {acl}(D)$
. Let
$e\in (\operatorname {acl}(AD)\cap \operatorname {acl}(BD))\backslash \operatorname {acl}(D)$
. Let
![]() $\overline {a}$
be a finite tuple from A of minimal length such that
$\overline {a}$
be a finite tuple from A of minimal length such that
![]() $e\in \operatorname {acl}(\overline {a}D)$
. Note that
$e\in \operatorname {acl}(\overline {a}D)$
. Note that
![]() $\overline {a}$
is nonempty (since
$\overline {a}$
is nonempty (since
![]() $e\not \in \operatorname {acl}(D)$
) and algebraically independent over D. Write
$e\not \in \operatorname {acl}(D)$
) and algebraically independent over D. Write
![]() $\overline {a}=a_0\overline {a}'$
where
$\overline {a}=a_0\overline {a}'$
where
![]() $a_0$
is a singleton. Then
$a_0$
is a singleton. Then
![]() $e\in \operatorname {acl}(a_0\overline {a}'D)\backslash \operatorname {acl}(\overline {a}'D)$
, hence by exchange
$e\in \operatorname {acl}(a_0\overline {a}'D)\backslash \operatorname {acl}(\overline {a}'D)$
, hence by exchange
![]() $a_0\in \operatorname {acl}(e\overline {a}'D)\subseteq \operatorname {acl}(\overline {a}'BC)$
. Now let
$a_0\in \operatorname {acl}(e\overline {a}'D)\subseteq \operatorname {acl}(\overline {a}'BC)$
. Now let
![]() $\overline {b}$
be a finite tuple from B of minimal length such that
$\overline {b}$
be a finite tuple from B of minimal length such that
![]() $a_0\in \operatorname {acl}(\overline {a}'\overline {b}C)$
. Again,
$a_0\in \operatorname {acl}(\overline {a}'\overline {b}C)$
. Again,
![]() $\overline {b}$
is nonempty (since
$\overline {b}$
is nonempty (since
![]() $\overline {a}$
is algebraically independent over D, and hence over C as well) and algebraically independent over
$\overline {a}$
is algebraically independent over D, and hence over C as well) and algebraically independent over
![]() $\overline {a}'C$
. Write
$\overline {a}'C$
. Write
![]() $\overline {b}=b_0\overline {b}'$
where
$\overline {b}=b_0\overline {b}'$
where
![]() $b_0$
is a singleton. Then
$b_0$
is a singleton. Then
![]() $a_0\in \operatorname {acl}(\overline {a}'b_0\overline {b}'C)\backslash \operatorname {acl}(\overline {a}'\overline {b}'C)$
, hence by exchange
$a_0\in \operatorname {acl}(\overline {a}'b_0\overline {b}'C)\backslash \operatorname {acl}(\overline {a}'\overline {b}'C)$
, hence by exchange
![]() $b_0\in \operatorname {acl}(\overline {a}\overline {b}' C)$
. Recall that
$b_0\in \operatorname {acl}(\overline {a}\overline {b}' C)$
. Recall that
![]() $\overline {b}'$
is algebraically independent over
$\overline {b}'$
is algebraically independent over
![]() $\overline {a}'C$
, hence over C, so
$\overline {a}'C$
, hence over C, so
![]() $b_0\not \in \operatorname {acl}(\overline {b}'C)$
. Altogether,
$b_0\not \in \operatorname {acl}(\overline {b}'C)$
. Altogether,
![]() $b_0$
witnesses
$b_0$
witnesses ![]() . Therefore
. Therefore ![]() . By base monotonicity for
. By base monotonicity for ![]() , and since
, and since
![]() $\bar {b}'$
is a tuple from B, we conclude
$\bar {b}'$
is a tuple from B, we conclude ![]() , as desired.
, as desired.
2.4. Conclusion
In the spirit of Adler’s work, a natural thing to do at this point is to construct a new ternary relation by forcing algebraic extension on ![]() . So we define:
. So we define:
Then ![]() satisfies all of the properties that Remarks 5.4(3) and 5.4(4) of [Reference Adler3] intended for
satisfies all of the properties that Remarks 5.4(3) and 5.4(4) of [Reference Adler3] intended for ![]() . In particular,
. In particular, ![]() preserves algebraic closure and we have
preserves algebraic closure and we have
Note also that ![]() satisfies existence (by Remark 2.10). Moreover,
satisfies existence (by Remark 2.10). Moreover, ![]() if and only if forking and dividing are the same for complete types over algebraically closed sets.
if and only if forking and dividing are the same for complete types over algebraically closed sets.
Altogether, perhaps ![]() is the more natural notion of “dividing independence” in an arbitrary theory. For example, by replacing
is the more natural notion of “dividing independence” in an arbitrary theory. For example, by replacing ![]() with
with ![]() , we obtain the following variations of the (formerly) open questions discussed in the introduction.
, we obtain the following variations of the (formerly) open questions discussed in the introduction.
Question 2.20. Let T be a complete theory.
-
(1) Suppose
 satisfies existence. Do
satisfies existence. Do  and
and  coincide?
coincide? -
(2) Suppose T is
 $\mathrm {NSOP}$
(or even just
$\mathrm {NSOP}$
(or even just
 $\mathrm {NSOP}_1$
). Do
$\mathrm {NSOP}_1$
). Do  and
and  coincide (even just over models)?
coincide (even just over models)?
Implicit in these questions is the third question of whether there is an
![]() $\mathrm {NSOP}$
theory in which
$\mathrm {NSOP}$
theory in which ![]() fails existence. In fact, this is open even for
fails existence. In fact, this is open even for
![]() $\mathrm {NSOP}_1$
theories, and is a question of notable significance for this region due to the results of [Reference Dobrowolski, Kim and Ramsey15]. We also note that for T
$\mathrm {NSOP}_1$
theories, and is a question of notable significance for this region due to the results of [Reference Dobrowolski, Kim and Ramsey15]. We also note that for T
![]() $\mathrm {NSOP}_1$
, the second question is a stronger version of [Reference Kaplan and Ramsey17, Question 9.19], which asks whether
$\mathrm {NSOP}_1$
, the second question is a stronger version of [Reference Kaplan and Ramsey17, Question 9.19], which asks whether ![]() for all sets A and models
for all sets A and models
![]() $M\prec N\prec \mathbb M\models T$
.
$M\prec N\prec \mathbb M\models T$
.
3. The counterexamples
3.1. Dense circular order with unordered pairs
In this section, we describe a very straightforward example of the failure of algebraic extension for ![]() (refuting [Reference Adler3, Remark 5.4(3)]).
(refuting [Reference Adler3, Remark 5.4(3)]).
Let
![]() $T=\mathrm {Th}({\mathbb Q},\operatorname {cyc})^{\mathrm {eq}}$
, where
$T=\mathrm {Th}({\mathbb Q},\operatorname {cyc})^{\mathrm {eq}}$
, where
Let O be the home sort, and let P be the sort corresponding to the definable equivalence relation E defined by
![]() $(x,y)E(x',y')$
if and only if
$(x,y)E(x',y')$
if and only if
![]() $\{x,y\} = \{x',y'\}$
. So the elements of P can be identified with the unordered pairs and singletons from O. Let
$\{x,y\} = \{x',y'\}$
. So the elements of P can be identified with the unordered pairs and singletons from O. Let
![]() $q\colon O^2\to P$
be the quotient map. Working in
$q\colon O^2\to P$
be the quotient map. Working in
![]() $\mathbb M\models T$
, let
$\mathbb M\models T$
, let
![]() $a,d_1,d_2$
be three distinct elements of the home sort with
$a,d_1,d_2$
be three distinct elements of the home sort with
![]() $\operatorname {cyc}(d_1,a,d_2)$
, and let
$\operatorname {cyc}(d_1,a,d_2)$
, and let
![]() $b=q(d_1,d_2)$
.
$b=q(d_1,d_2)$
.
Claim 3.1.
![]() , but
, but ![]() .
.
Proof First, since
![]() $d_1,d_2\in \operatorname {acl}(b)$
, and the formula
$d_1,d_2\in \operatorname {acl}(b)$
, and the formula
![]() $\operatorname {cyc}(d_1,x,d_2)$
divides over
$\operatorname {cyc}(d_1,x,d_2)$
divides over
![]() $\varnothing $
, we have
$\varnothing $
, we have ![]() . So we need to show
. So we need to show ![]() . We start with a general remark. Suppose
. We start with a general remark. Suppose
![]() $a'$
,
$a'$
,
![]() $d^{\prime }_1$
,
$d^{\prime }_1$
,
![]() $d^{\prime }_2$
are any pairwise distinct elements of O, and set
$d^{\prime }_2$
are any pairwise distinct elements of O, and set
![]() $b'=q(d^{\prime }_1,d^{\prime }_2)$
. Then either
$b'=q(d^{\prime }_1,d^{\prime }_2)$
. Then either
![]() $\operatorname {cyc}(d^{\prime }_1,a',d^{\prime }_2)$
, in which case we have an isomorphism
$\operatorname {cyc}(d^{\prime }_1,a',d^{\prime }_2)$
, in which case we have an isomorphism
![]() $ad_1d_2\to a'd^{\prime }_1d^{\prime }_2$
, or
$ad_1d_2\to a'd^{\prime }_1d^{\prime }_2$
, or
![]() $\operatorname {cyc}(d^{\prime }_2,a',d^{\prime }_1)$
, in which case we have an isomorphism
$\operatorname {cyc}(d^{\prime }_2,a',d^{\prime }_1)$
, in which case we have an isomorphism
![]() $ad_1d_2\to a'd^{\prime }_2d^{\prime }_1$
. In either case, by quantifier elimination this yields
$ad_1d_2\to a'd^{\prime }_2d^{\prime }_1$
. In either case, by quantifier elimination this yields
![]() $a'b'\equiv _\varnothing ab$
.
$a'b'\equiv _\varnothing ab$
.
Now let
![]() $(b_n)_{n<\omega }$
be an indiscernible sequence in
$(b_n)_{n<\omega }$
be an indiscernible sequence in
![]() $\operatorname {tp}(b/\varnothing )$
. For each n, let
$\operatorname {tp}(b/\varnothing )$
. For each n, let
![]() ${b_n=q(d^n_1,d^n_2)}$
, and note that
${b_n=q(d^n_1,d^n_2)}$
, and note that
![]() $d^n_1\neq d^n_2$
. Choose
$d^n_1\neq d^n_2$
. Choose
![]() $a'$
from the home sort distinct from
$a'$
from the home sort distinct from
![]() $d^n_1,d^n_2$
for all
$d^n_1,d^n_2$
for all
![]() $n<\omega $
. Then, by the above, we have
$n<\omega $
. Then, by the above, we have
![]() $a'b_n\equiv _\varnothing ab$
for all
$a'b_n\equiv _\varnothing ab$
for all
![]() $n<\omega $
, so
$n<\omega $
, so ![]() , as desired.
, as desired.
We conclude that in T, ![]() fails algebraic extension over
fails algebraic extension over
![]() $\varnothing $
. To recap the discussion from the introduction, note that T is an NIP theory, and that
$\varnothing $
. To recap the discussion from the introduction, note that T is an NIP theory, and that
![]() $\varnothing $
is (necessarily) not an extension base for nonforking.
$\varnothing $
is (necessarily) not an extension base for nonforking.
3.2. Generic binary function with unordered pairs
In this section, we give another example of a theory in which ![]() fails algebraic extension. Like before, this theory will be the imaginary expansion of a well-known example from the literature. However, in this case we will have better behavior related to forking (compared to the circular order on
fails algebraic extension. Like before, this theory will be the imaginary expansion of a well-known example from the literature. However, in this case we will have better behavior related to forking (compared to the circular order on
![]() ${\mathbb Q}$
), and thus the failure of algebraic extension for
${\mathbb Q}$
), and thus the failure of algebraic extension for ![]() will have more interesting consequences.
will have more interesting consequences.
Let
![]() $T^{\varnothing }_f$
be the model completion of the empty theory in a language containing only a binary function symbol f. Then
$T^{\varnothing }_f$
be the model completion of the empty theory in a language containing only a binary function symbol f. Then
![]() $T^{\varnothing }_f$
is
$T^{\varnothing }_f$
is
![]() $\mathrm {NSOP}_1$
by [Reference Kruckman and Ramsey20], and thus so is the imaginary expansion, which we denote
$\mathrm {NSOP}_1$
by [Reference Kruckman and Ramsey20], and thus so is the imaginary expansion, which we denote
![]() $T^{\mathrm {eq}}_f$
. We will prove that
$T^{\mathrm {eq}}_f$
. We will prove that
![]() $T^{\mathrm {eq}}_f$
has the following properties:
$T^{\mathrm {eq}}_f$
has the following properties:
-
(1) For any small model M,
 does not imply
does not imply  . So in addition to implying the failure of algebraic extension for
. So in addition to implying the failure of algebraic extension for  (even over models), this also refutes the weaker claim made in [Reference Adler3, Remark 5.4
(even over models), this also refutes the weaker claim made in [Reference Adler3, Remark 5.4
 $(4)$
].
$(4)$
]. -
(2) Consequently,
 , even over models, which gives a negative answer to an open question about
, even over models, which gives a negative answer to an open question about
 $\mathrm {NSOP}_1$
theories (discussed in the introduction).
$\mathrm {NSOP}_1$
theories (discussed in the introduction). -
(3) All sets are extension bases for nonforking in
 $T^{\mathrm {eq}}_f$
. So this theory also gives a negative answer to [Reference Adler1, Question A.1], which asks whether forking and dividing are always the same for complete types in such a theory.
$T^{\mathrm {eq}}_f$
. So this theory also gives a negative answer to [Reference Adler1, Question A.1], which asks whether forking and dividing are always the same for complete types in such a theory.
Toward obtaining these statements, we first recall from Corollaries 3.10 and 3.11 of [Reference Kruckman and Ramsey20] that
![]() $T^{\varnothing }_f$
has quantifier elimination and the algebraic closure of any set coincides with the substructure generated by that set. Moving now to
$T^{\varnothing }_f$
has quantifier elimination and the algebraic closure of any set coincides with the substructure generated by that set. Moving now to
![]() $T^{\mathrm {eq}}_f$
, we work in a similar setting as in the previous subsection. Let O be the home sort, and let P be the sort corresponding to the definable equivalence relation E defined by
$T^{\mathrm {eq}}_f$
, we work in a similar setting as in the previous subsection. Let O be the home sort, and let P be the sort corresponding to the definable equivalence relation E defined by
![]() $(x,y)E(x',y')$
if and only if
$(x,y)E(x',y')$
if and only if
![]() $\{x,y\} = \{x',y'\}$
. So as before, the elements of P can be identified with the unordered pairs and singletons from O. Let
$\{x,y\} = \{x',y'\}$
. So as before, the elements of P can be identified with the unordered pairs and singletons from O. Let
![]() $q\colon O^2\to P$
be the quotient map. We write
$q\colon O^2\to P$
be the quotient map. We write
![]() $\operatorname {acl}^O(x)$
for the elements of the home sort which are algebraic over x.
$\operatorname {acl}^O(x)$
for the elements of the home sort which are algebraic over x.
Let M be a small model of
![]() $T^{\mathrm {eq}}_f$
, and write
$T^{\mathrm {eq}}_f$
, and write
![]() $M^O$
for its home sort. Let
$M^O$
for its home sort. Let
![]() $d_1$
and
$d_1$
and
![]() $d_2$
be distinct elements of the home sort, which are not in M, such that
$d_2$
be distinct elements of the home sort, which are not in M, such that
![]() $f(d_i,d_j) = d_i$
for all
$f(d_i,d_j) = d_i$
for all
![]() $i,j\in \{1,2\}$
and
$i,j\in \{1,2\}$
and
![]() $f(m,d_k) = f(d_k,m) = d_k$
for all
$f(m,d_k) = f(d_k,m) = d_k$
for all
![]() $k\in \{1,2\}$
and all
$k\in \{1,2\}$
and all
![]() $m\in M^O$
. Let
$m\in M^O$
. Let
![]() $b = q(d_1,d_2)$
.
$b = q(d_1,d_2)$
.
Note that
![]() $\operatorname {acl}^O(Mb) = \operatorname {acl}^O(Md_1d_2) = \langle M^O d_1 d_2\rangle = M^O\cup \{d_1,d_2\}$
, and the map swapping
$\operatorname {acl}^O(Mb) = \operatorname {acl}^O(Md_1d_2) = \langle M^O d_1 d_2\rangle = M^O\cup \{d_1,d_2\}$
, and the map swapping
![]() $d_1$
and
$d_1$
and
![]() $d_2$
and fixing M pointwise is an automorphism of this substructure. Also,
$d_2$
and fixing M pointwise is an automorphism of this substructure. Also,
![]() $\operatorname {acl}^O(Md_i) = \langle M^Od_i\rangle = M^O\cup \{d_i\}$
for all
$\operatorname {acl}^O(Md_i) = \langle M^Od_i\rangle = M^O\cup \{d_i\}$
for all
![]() $i\in \{1,2\}$
.
$i\in \{1,2\}$
.
Now let a be an element of the home sort such that
![]() $f(a,a) = a$
,
$f(a,a) = a$
,
![]() $f(a,m) = f(m,a) = a$
for all
$f(a,m) = f(m,a) = a$
for all
![]() $m\in M$
,
$m\in M$
,
![]() $f(a,d_1) = f(d_1,a) = a$
, and
$f(a,d_1) = f(d_1,a) = a$
, and
![]() $f(a,d_2) = f(d_2,a) = d_1$
. Then
$f(a,d_2) = f(d_2,a) = d_1$
. Then
![]() $\operatorname {acl}^O(Mad_1) = \langle M^Oad_1\rangle = M^O\cup \{a,d_1\}$
, while
$\operatorname {acl}^O(Mad_1) = \langle M^Oad_1\rangle = M^O\cup \{a,d_1\}$
, while
![]() $\operatorname {acl}^O(Mad_2) = \langle M^Oad_2\rangle = M^O\cup \{a,d_1,d_2\} = \operatorname {acl}^O(Mad_1d_2)$
.
$\operatorname {acl}^O(Mad_2) = \langle M^Oad_2\rangle = M^O\cup \{a,d_1,d_2\} = \operatorname {acl}^O(Mad_1d_2)$
.
Claim 3.2.
![]() , but
, but ![]() and
and ![]() .
.
Proof First note that
![]() $d_1\in \operatorname {acl}(Mad_2)\cap \operatorname {acl}(Mb)$
, but
$d_1\in \operatorname {acl}(Mad_2)\cap \operatorname {acl}(Mb)$
, but
![]() $d_1\notin \operatorname {acl}(Md_2)$
. So
$d_1\notin \operatorname {acl}(Md_2)$
. So ![]() . Since
. Since
![]() $d_2\in \operatorname {acl}(Mb)$
, we have
$d_2\in \operatorname {acl}(Mb)$
, we have ![]() and
and ![]() .
.
Now we show ![]() . Let
. Let
![]() $a'$
be an element of O and
$a'$
be an element of O and
![]() $b'$
an element of P, with
$b'$
an element of P, with
![]() $b' = q(d_1',d_2')$
. By quantifier elimination,
$b' = q(d_1',d_2')$
. By quantifier elimination,
![]() $ab\equiv _M a'b'$
if and only if there is an isomorphism
$ab\equiv _M a'b'$
if and only if there is an isomorphism
![]() $\langle Mad_1d_2\rangle \to \langle Ma'd_1'd_2'\rangle $
, fixing M pointwise, with
$\langle Mad_1d_2\rangle \to \langle Ma'd_1'd_2'\rangle $
, fixing M pointwise, with
![]() $a\mapsto a'$
and either
$a\mapsto a'$
and either
![]() $d_1\mapsto d_1'$
and
$d_1\mapsto d_1'$
and
![]() $d_2\mapsto d_2'$
, or
$d_2\mapsto d_2'$
, or
![]() $d_1\mapsto d_2'$
and
$d_1\mapsto d_2'$
and
![]() $d_2\mapsto d_1'$
.
$d_2\mapsto d_1'$
.
Let
![]() $(b_n)_{n< \omega }$
be an M-indiscernible sequence in
$(b_n)_{n< \omega }$
be an M-indiscernible sequence in
![]() $\text {tp}(b/M)$
. For each n, let
$\text {tp}(b/M)$
. For each n, let
![]() ${b_n = q(d^n_1,d^n_2)}$
, and note that
${b_n = q(d^n_1,d^n_2)}$
, and note that
![]() $d^n_1\neq d^n_2$
and
$d^n_1\neq d^n_2$
and
![]() $f(d^n_i,d^n_j) = d^n_i$
for all
$f(d^n_i,d^n_j) = d^n_i$
for all
![]() $i,j\in \{1,2\}$
. Without loss of generality, we can enumerate
$i,j\in \{1,2\}$
. Without loss of generality, we can enumerate
![]() $d^n_1$
and
$d^n_1$
and
![]() $d^n_2$
so that the sequence
$d^n_2$
so that the sequence
![]() $(b_nd^n_1d^n_2)_{n< \omega }$
is M-indiscernible.
$(b_nd^n_1d^n_2)_{n< \omega }$
is M-indiscernible.
Case 1: For all
![]() $n\neq m$
,
$n\neq m$
,
![]() $d^n_2 \neq d^m_2$
. Then we can find an
$d^n_2 \neq d^m_2$
. Then we can find an
![]() $a'$
such that
$a'$
such that
![]() $f(a',a') = a'$
,
$f(a',a') = a'$
,
![]() $f(a',m) = f(m,a') = a'$
for all
$f(a',m) = f(m,a') = a'$
for all
![]() $m\in M$
,
$m\in M$
,
![]() $f(a',d^n_1) = f(d^n_1,a') = a'$
, and
$f(a',d^n_1) = f(d^n_1,a') = a'$
, and
![]() $f(a',d^n_2) = f(d^n_2,a') = d^n_1$
for all n. Then
$f(a',d^n_2) = f(d^n_2,a') = d^n_1$
for all n. Then
![]() $a'b_n \equiv _M ab$
for all n.
$a'b_n \equiv _M ab$
for all n.
Case 2: For all
![]() $n\neq m$
,
$n\neq m$
,
![]() $d^n_2 = d^m_2$
. In this case, if
$d^n_2 = d^m_2$
. In this case, if
![]() $d^n_1\neq d^m_1$
, we cannot find
$d^n_1\neq d^m_1$
, we cannot find
![]() $a'$
such that
$a'$
such that
![]() $f(a',d^n_2) = d^n_1$
and
$f(a',d^n_2) = d^n_1$
and
![]() $f(a',d^m_2) = d^m_1$
. However, we can find an
$f(a',d^m_2) = d^m_1$
. However, we can find an
![]() $a'$
such that
$a'$
such that
![]() $f(a',a') = a'$
,
$f(a',a') = a'$
,
![]() $f(a',m) = f(m,a') = a'$
for all
$f(a',m) = f(m,a') = a'$
for all
![]() $m\in M$
,
$m\in M$
,
![]() $f(a',d^n_2) = f(d^n_2,a') = a'$
, and
$f(a',d^n_2) = f(d^n_2,a') = a'$
, and
![]() $f(a',d^n_1) = f(d^n_1,a') = d^n_2$
for all n. Then
$f(a',d^n_1) = f(d^n_1,a') = d^n_2$
for all n. Then
![]() $a'b_n \equiv _M ab$
for all n (though in this case the witnessing isomorphisms map
$a'b_n \equiv _M ab$
for all n (though in this case the witnessing isomorphisms map
![]() $d^n_1\mapsto d_2$
and
$d^n_1\mapsto d_2$
and
![]() $d^n_2\mapsto d_1$
).
$d^n_2\mapsto d_1$
).
In either case, we have an
![]() $a'$
such that
$a'$
such that
![]() $a'b_n \equiv _M ab$
for all
$a'b_n \equiv _M ab$
for all
![]() $n<\omega $
, so
$n<\omega $
, so ![]() .
.
Corollary 3.3.
![]() does not necessarily imply
does not necessarily imply ![]() in general. Moreover,
in general. Moreover, ![]() does not necessarily imply
does not necessarily imply ![]() in
in
![]() $\mathrm {NSOP}_1$
theories, even over models.
$\mathrm {NSOP}_1$
theories, even over models.
Explicitly, in
![]() $T^{\mathrm {eq}}_f$
the formula
$T^{\mathrm {eq}}_f$
the formula
![]() $\exists w_1\exists w_2\,(q(w_1,w_2) = b\land f(x,w_2) = w_1)$
in
$\exists w_1\exists w_2\,(q(w_1,w_2) = b\land f(x,w_2) = w_1)$
in
![]() $\operatorname {tp}(a/Mb)$
forks but does not divide. It implies the disjunction
$\operatorname {tp}(a/Mb)$
forks but does not divide. It implies the disjunction
![]() $f(x,d_2) = d_1\lor f(x,d_1) = d_2$
, and each disjunct divides over M.
$f(x,d_2) = d_1\lor f(x,d_1) = d_2$
, and each disjunct divides over M.
We have now established statements
![]() $(1)$
and
$(1)$
and
![]() $(2)$
above. For
$(2)$
above. For
![]() $(3)$
, we need the following general observation.
$(3)$
, we need the following general observation.
Proposition 3.4. Suppose T is a complete theory with geometric elimination of imaginaries.
-
(a) Assume
 satisfies existence in T. Then
satisfies existence in T. Then  satisfies existence in
satisfies existence in
 $T^{\mathrm {eq}}$
.
$T^{\mathrm {eq}}$
. -
(b) Assume
 in T. Then
in T. Then  in
in
 $T^{\mathrm {eq}}$
.
$T^{\mathrm {eq}}$
.
Proof We prove part
![]() $(b)$
and leave
$(b)$
and leave
![]() $(a)$
(which is similar and easier) to the reader. Fix
$(a)$
(which is similar and easier) to the reader. Fix
![]() $A,B,C\subseteq \mathbb M^{\mathrm {eq}}$
and assume
$A,B,C\subseteq \mathbb M^{\mathrm {eq}}$
and assume ![]() in
in
![]() $T^{\mathrm {eq}}$
. We need to show
$T^{\mathrm {eq}}$
. We need to show ![]() in
in
![]() $T^{\mathrm {eq}}$
. Without loss of generality, assume
$T^{\mathrm {eq}}$
. Without loss of generality, assume
![]() $C\subseteq A\cap B$
. By geometric elimination of imaginaries, there are real sets
$C\subseteq A\cap B$
. By geometric elimination of imaginaries, there are real sets
![]() $A',B',C'\subseteq \mathbb M$
such that
$A',B',C'\subseteq \mathbb M$
such that
![]() $\operatorname {acl}^{\mathrm {eq}}(A)=\operatorname {acl}^{\mathrm {eq}}(A')$
,
$\operatorname {acl}^{\mathrm {eq}}(A)=\operatorname {acl}^{\mathrm {eq}}(A')$
,
![]() $\operatorname {acl}^{\mathrm {eq}}(B)=\operatorname {acl}^{\mathrm {eq}}(B')$
, and
$\operatorname {acl}^{\mathrm {eq}}(B)=\operatorname {acl}^{\mathrm {eq}}(B')$
, and
![]() $\operatorname {acl}^{\mathrm {eq}}(C)=\operatorname {acl}^{\mathrm {eq}}(C')$
. Since
$\operatorname {acl}^{\mathrm {eq}}(C)=\operatorname {acl}^{\mathrm {eq}}(C')$
. Since ![]() preserves algebraic closure, we have
preserves algebraic closure, we have ![]() . By monotonicity for
. By monotonicity for ![]() and Proposition 2.7, this yields
and Proposition 2.7, this yields ![]() in
in
![]() $T^{\mathrm {eq}}$
, and hence also in T. So
$T^{\mathrm {eq}}$
, and hence also in T. So ![]() in T, and thus
in T, and thus ![]() in T by assumption. Therefore
in T by assumption. Therefore ![]() in
in
![]() $T^{\mathrm {eq}}$
, which yields
$T^{\mathrm {eq}}$
, which yields ![]() in
in
![]() $T^{\mathrm {eq}}$
using Proposition 2.12 and the choice of
$T^{\mathrm {eq}}$
using Proposition 2.12 and the choice of
![]() $A'$
,
$A'$
,
![]() $B'$
, and
$B'$
, and
![]() $C'$
.
$C'$
.
Now, to obtain statement
![]() $(3)$
above, we recall the results from [Reference Kruckman and Ramsey20] that
$(3)$
above, we recall the results from [Reference Kruckman and Ramsey20] that
![]() $T^{\varnothing }_f$
has weak elimination of imaginaries and satisfies
$T^{\varnothing }_f$
has weak elimination of imaginaries and satisfies ![]() (see Section 5.1 for further related discussion). So
(see Section 5.1 for further related discussion). So ![]() satisfies existence in
satisfies existence in
![]() $T^{\mathrm {eq}}_f$
by the previous proposition. Note that this conclusion only requires part
$T^{\mathrm {eq}}_f$
by the previous proposition. Note that this conclusion only requires part
![]() $(a)$
; however part
$(a)$
; however part
![]() $(b)$
gives us the stronger statement that
$(b)$
gives us the stronger statement that ![]() in
in
![]() $T^{\mathrm {eq}}_f$
(cf. Question 2.20).
$T^{\mathrm {eq}}_f$
(cf. Question 2.20).
Remark 3.5. Since ![]() is true in
is true in
![]() $T^{\varnothing }_f$
but not in
$T^{\varnothing }_f$
but not in
![]() $T^{\mathrm {eq}}_f$
, our example shows that the property
$T^{\mathrm {eq}}_f$
, our example shows that the property ![]() does not transfer from T to
does not transfer from T to
![]() $T^{\mathrm {eq}}$
, even when T has weak elimination of imaginaries. This is in contrast to the properties
$T^{\mathrm {eq}}$
, even when T has weak elimination of imaginaries. This is in contrast to the properties ![]() and existence for
and existence for ![]() in Proposition 3.4.
in Proposition 3.4.
3.3. The original counterexample
In this section, we construct a complete theory for which ![]() does not have algebraic extension due to a failure of the weaker axiom discussed in Remark 2.9. Specifically, there are
does not have algebraic extension due to a failure of the weaker axiom discussed in Remark 2.9. Specifically, there are
![]() $a,b\in \mathbb M$
such that
$a,b\in \mathbb M$
such that ![]() and
and ![]() . This is also the original counterexample first discovered by the second-named author to refute [Reference Adler3, Remark 5.4(3)].
. This is also the original counterexample first discovered by the second-named author to refute [Reference Adler3, Remark 5.4(3)].
The example we construct will be the theory of a Fraïssé limit for a Fraïssé class with free amalgamation. We briefly recall the definition of free amalgamation. Given a (many-sorted) language
![]() $\mathcal L$
with only relation symbols and constant symbols, and three
$\mathcal L$
with only relation symbols and constant symbols, and three
![]() $\mathcal L$
-structures A, B, C, where C is a common substructure of A and B, the free amalgam of A and B over C is the
$\mathcal L$
-structures A, B, C, where C is a common substructure of A and B, the free amalgam of A and B over C is the
![]() $\mathcal L$
-structure D defined as follows. For each sort S,
$\mathcal L$
-structure D defined as follows. For each sort S,
![]() $S(D) = S(A)\sqcup _{S(C)} S(B)$
, the disjoint union of
$S(D) = S(A)\sqcup _{S(C)} S(B)$
, the disjoint union of
![]() $S(A)$
and
$S(A)$
and
![]() $S(B)$
over
$S(B)$
over
![]() $S(C)$
. For each relation symbol R in
$S(C)$
. For each relation symbol R in
![]() $\mathcal L$
,
$\mathcal L$
,
![]() $R^D = R^A\cup R^B$
. That is, no relations hold in D, other than those which hold in A and in B. The constant symbols in
$R^D = R^A\cup R^B$
. That is, no relations hold in D, other than those which hold in A and in B. The constant symbols in
![]() $\mathcal L$
receive the same interpretation in D as in A, B, and C. We say that a class of finite
$\mathcal L$
receive the same interpretation in D as in A, B, and C. We say that a class of finite
![]() $\mathcal L$
-structures has free amalgamation if whenever A, B, and C are in the class, and C is a common substructure of A and B, the free amalgam of A and B over C is again in the class.
$\mathcal L$
-structures has free amalgamation if whenever A, B, and C are in the class, and C is a common substructure of A and B, the free amalgam of A and B over C is again in the class.
We now describe our example. Consider a language
![]() $\mathcal L'$
with:
$\mathcal L'$
with:
-
* Three sorts: O, G, and C.
-
* Two constant symbols
 $0$
and
$0$
and
 $1$
of type C.
$1$
of type C. -
* A relation symbol R of type
 $G\times G \times C$
.
$G\times G \times C$
. -
* A relation symbol E of type
 $O\times G \times C$
.
$O\times G \times C$
.
Let
![]() $\mathcal {K}$
be the class of finite
$\mathcal {K}$
be the class of finite
![]() $\mathcal L'$
-structures satisfying the following conditions:
$\mathcal L'$
-structures satisfying the following conditions:
-
(1)
 $0\neq 1$
, and for all
$0\neq 1$
, and for all
 $c\in C$
,
$c\in C$
,
 $c = 0$
or
$c = 0$
or
 $c = 1$
.
$c = 1$
. -
(2) The binary relations
 $R(x,y,0)$
and
$R(x,y,0)$
and
 $R(x,y,1)$
are disjoint graph relations on G, i.e., they are each symmetric and anti-reflexive, and for all
$R(x,y,1)$
are disjoint graph relations on G, i.e., they are each symmetric and anti-reflexive, and for all
 $v,w\in G$
, it is not the case that
$v,w\in G$
, it is not the case that
 $R(v,w,0)$
and
$R(v,w,0)$
and
 $R(v,w,1)$
.
$R(v,w,1)$
. -
(3) For all
 $v,w\in G$
and
$v,w\in G$
and
 $c\in C$
, if
$c\in C$
, if
 $R(v,w,c)$
, then there is no
$R(v,w,c)$
, then there is no
 $o\in O$
such that
$o\in O$
such that
 $E(o,v,c)$
and
$E(o,v,c)$
and
 $E(o,w,c)$
.
$E(o,w,c)$
.
It is easy to check that
![]() $\mathcal {K}$
is a Fraïssé class with free amalgamation. Let
$\mathcal {K}$
is a Fraïssé class with free amalgamation. Let
![]() $M'$
be the Fraïssé limit of
$M'$
be the Fraïssé limit of
![]() $\mathcal {K}$
.
$\mathcal {K}$
.
Now let
![]() $\mathcal L$
be the sub-language of
$\mathcal L$
be the sub-language of
![]() $\mathcal L'$
which omits the constant symbols
$\mathcal L'$
which omits the constant symbols
![]() $0$
and
$0$
and
![]() $1$
. Let M be the reduct of
$1$
. Let M be the reduct of
![]() $M'$
to
$M'$
to
![]() $\mathcal L$
, and set
$\mathcal L$
, and set
![]() $T_{\mathsf {OG}}=\mathrm {Th}(M)$
. We observe the following:
$T_{\mathsf {OG}}=\mathrm {Th}(M)$
. We observe the following:
-
(i)
 $T_{\mathsf {OG}}$
is
$T_{\mathsf {OG}}$
is
 $\aleph _0$
-categorical. Indeed, it is a reduct of a Fraïssé limit of a class of finite structures in a finite language with no function symbols.
$\aleph _0$
-categorical. Indeed, it is a reduct of a Fraïssé limit of a class of finite structures in a finite language with no function symbols. -
(ii) For any
 $A\subseteq M$
,
$A\subseteq M$
,
 $\operatorname {acl}(A) = A\cup C$
. Indeed,
$\operatorname {acl}(A) = A\cup C$
. Indeed,
 $A\cup C$
is the domain of a substructure of
$A\cup C$
is the domain of a substructure of
 $M'$
. Since amalgamation in
$M'$
. Since amalgamation in
 $\mathcal {K}$
is disjoint,
$\mathcal {K}$
is disjoint,
 $A\cup C$
is algebraically closed in
$A\cup C$
is algebraically closed in
 $M'$
, so it remains algebraically closed in the reduct M.
$M'$
, so it remains algebraically closed in the reduct M. -
(iii) There is an automorphism
 $\sigma $
of M swapping the two elements of C. This can be established by a back-and-forth argument.
$\sigma $
of M swapping the two elements of C. This can be established by a back-and-forth argument. -
(iv) For any finite tuples a and b from M,
 $\operatorname {tp}(a) = \operatorname {tp}(b)$
if and only if there is an isomorphism of
$\operatorname {tp}(a) = \operatorname {tp}(b)$
if and only if there is an isomorphism of
 $\mathcal L$
-structures
$\mathcal L$
-structures
 $f\colon \operatorname {acl}(a)\to \operatorname {acl}(b)$
such that
$f\colon \operatorname {acl}(a)\to \operatorname {acl}(b)$
such that
 $f(a) = b$
. The forward direction follows from
$f(a) = b$
. The forward direction follows from
 $\aleph _0$
-homogeneity of M. For the converse, suppose
$\aleph _0$
-homogeneity of M. For the converse, suppose
 $f\colon \operatorname {acl}(a)\to \operatorname {acl}(b)$
is such an isomorphism. If f is the identity on C, then it is an isomorphism between
$f\colon \operatorname {acl}(a)\to \operatorname {acl}(b)$
is such an isomorphism. If f is the identity on C, then it is an isomorphism between
 $\mathcal L'$
-substructures of
$\mathcal L'$
-substructures of
 $M'$
, so it extends to an automorphism of
$M'$
, so it extends to an automorphism of
 $M'$
moving a to b, and hence
$M'$
moving a to b, and hence
 $\operatorname {tp}(a) = \operatorname {tp}(b)$
. If f swaps the two elements of C, let
$\operatorname {tp}(a) = \operatorname {tp}(b)$
. If f swaps the two elements of C, let
 $f' = f\circ \sigma ^{-1}\colon \sigma (\operatorname {acl}(a))\to \operatorname {acl}(b)$
, where
$f' = f\circ \sigma ^{-1}\colon \sigma (\operatorname {acl}(a))\to \operatorname {acl}(b)$
, where
 $\sigma $
is an automorphism of M as in
$\sigma $
is an automorphism of M as in
 $(iii)$
above. Then
$(iii)$
above. Then
 $f'$
is an isomorphism which is the identity on C and such that
$f'$
is an isomorphism which is the identity on C and such that
 $f'(\sigma (a)) = b$
. Extending
$f'(\sigma (a)) = b$
. Extending
 $f'$
to an automorphism of
$f'$
to an automorphism of
 $M'$
as above, then pre-composing with
$M'$
as above, then pre-composing with
 $\sigma $
, we find an automorphism of M moving a to b, so
$\sigma $
, we find an automorphism of M moving a to b, so
 $\operatorname {tp}(a) = \operatorname {tp}(b)$
.
$\operatorname {tp}(a) = \operatorname {tp}(b)$
.
By
![]() $\aleph _0$
-categoricity, to understand dividing and the properties
$\aleph _0$
-categoricity, to understand dividing and the properties
![]() $\mathrm {SOP}_n$
in
$\mathrm {SOP}_n$
in
![]() $T_{\mathsf {OG}}$
, it suffices to work in M. We will refer to the elements of C as
$T_{\mathsf {OG}}$
, it suffices to work in M. We will refer to the elements of C as
![]() $0$
and
$0$
and
![]() $1$
(even though these constant symbols are not in
$1$
(even though these constant symbols are not in
![]() $\mathcal L$
).
$\mathcal L$
).
Claim 3.6.
![]() $T_{\mathsf {OG}}$
is
$T_{\mathsf {OG}}$
is
![]() $\mathrm {SOP}_3$
and
$\mathrm {SOP}_3$
and
![]() $\mathrm {NSOP}_4$
.
$\mathrm {NSOP}_4$
.
Proof Since
![]() $\mathrm {Th}(M')$
is the theory of an
$\mathrm {Th}(M')$
is the theory of an
![]() $\aleph _0$
-categorical Fraïssé limit with free amalgamation, it is
$\aleph _0$
-categorical Fraïssé limit with free amalgamation, it is
![]() $\mathrm {NSOP}_4$
. (This is an unpublished result of R. Patel [Reference Patel22]; see also [Reference Conant7, Section 4].) Therefore its reduct
$\mathrm {NSOP}_4$
. (This is an unpublished result of R. Patel [Reference Patel22]; see also [Reference Conant7, Section 4].) Therefore its reduct
![]() $T_{\mathsf {OG}}$
is also
$T_{\mathsf {OG}}$
is also
![]() $\mathrm {NSOP}_4$
. We will show that
$\mathrm {NSOP}_4$
. We will show that
![]() $T_{\mathsf {OG}}$
is
$T_{\mathsf {OG}}$
is
![]() $\mathrm {SOP}_3$
using the “two formula” formulation (see, e.g., [Reference Shelah23, Claim 2.19]). Let x be a variable of type O and
$\mathrm {SOP}_3$
using the “two formula” formulation (see, e.g., [Reference Shelah23, Claim 2.19]). Let x be a variable of type O and
![]() $y,y'$
variables of type G. Let
$y,y'$
variables of type G. Let
![]() $\varphi (x;y,y')$
be the formula
$\varphi (x;y,y')$
be the formula
![]() $E(x,y,0)$
, and let
$E(x,y,0)$
, and let
![]() $\varphi '(x;y,y')$
be the formula
$\varphi '(x;y,y')$
be the formula
![]() $E(x,y',0)$
. Let
$E(x,y',0)$
. Let
![]() $(b_i,b_i')_{i< \omega }$
be a sequence such that
$(b_i,b_i')_{i< \omega }$
be a sequence such that
![]() $R(b_i',b_j,0)$
if and only if
$R(b_i',b_j,0)$
if and only if
![]() $i< j$
. Then for all
$i< j$
. Then for all
![]() $n< \omega $
, we have
$n< \omega $
, we have
![]() $\{\varphi (x;b_i,b_i')\mid i < n\}\cup \{\varphi '(x;b_j,b_j')\mid j\geq n\}$
is consistent by genericity of the Fraïssé limit and compactness, but for all
$\{\varphi (x;b_i,b_i')\mid i < n\}\cup \{\varphi '(x;b_j,b_j')\mid j\geq n\}$
is consistent by genericity of the Fraïssé limit and compactness, but for all
![]() $i < j$
,
$i < j$
,
![]() $\{\varphi '(x;b_i,b_i'),\varphi (x;b_j,b_j')\}$
is inconsistent by condition (3) in the definition of
$\{\varphi '(x;b_i,b_i'),\varphi (x;b_j,b_j')\}$
is inconsistent by condition (3) in the definition of
![]() $\mathcal K$
. This establishes
$\mathcal K$
. This establishes
![]() $\mathrm {SOP}_3$
.
$\mathrm {SOP}_3$
.
We now show that
![]() $T_{\mathsf {OG}}$
exhibits the properties claimed at the start of this section.
$T_{\mathsf {OG}}$
exhibits the properties claimed at the start of this section.
Claim 3.7. Fix
![]() $a\in O$
and
$a\in O$
and
![]() $b\in G$
such that
$b\in G$
such that
![]() $E(a,b,0)$
and
$E(a,b,0)$
and
![]() $\lnot E(a,b,1)$
. Then
$\lnot E(a,b,1)$
. Then ![]() , but
, but ![]() .
.
Proof We first show ![]() . Let
. Let
![]() $(b_i)_{i< \omega }$
be an indiscernible sequence in
$(b_i)_{i< \omega }$
be an indiscernible sequence in
![]() $\text {tp}(b/\varnothing )$
.
$\text {tp}(b/\varnothing )$
.
Case 1:
![]() $M\models \lnot R(b_i,b_j,0)$
for all
$M\models \lnot R(b_i,b_j,0)$
for all
![]() $i\neq j$
. Then we can find some
$i\neq j$
. Then we can find some
![]() $a'\in O$
with
$a'\in O$
with
![]() $M\models E(a',b_i,0)\land \lnot E(a',b_i,1)$
for all
$M\models E(a',b_i,0)\land \lnot E(a',b_i,1)$
for all
![]() $i< \omega $
. The map
$i< \omega $
. The map
![]() $f_i\colon \operatorname {acl}(a'b_i)\to \operatorname {acl}(ab)$
which is the identity on C and maps
$f_i\colon \operatorname {acl}(a'b_i)\to \operatorname {acl}(ab)$
which is the identity on C and maps
![]() $a'$
to a and
$a'$
to a and
![]() $b_i$
to b is an isomorphism of
$b_i$
to b is an isomorphism of
![]() $\mathcal L$
-substructures of M, so
$\mathcal L$
-substructures of M, so
![]() $a'b_i\equiv ab$
for all
$a'b_i\equiv ab$
for all
![]() $i<\omega $
by
$i<\omega $
by
![]() $(iv)$
above.
$(iv)$
above.
Case 2: Otherwise, by indiscernibility,
![]() $M\models R(b_i,b_j,0)$
for all
$M\models R(b_i,b_j,0)$
for all
![]() $i\neq j$
. Since
$i\neq j$
. Since
![]() $R(x,y,0)$
and
$R(x,y,0)$
and
![]() $R(x,y,1)$
are disjoint relations,
$R(x,y,1)$
are disjoint relations,
![]() $M\models \lnot R(b_i,b_j,1)$
for all
$M\models \lnot R(b_i,b_j,1)$
for all
![]() $i\neq j$
. So we can find some
$i\neq j$
. So we can find some
![]() $a'\in O$
with
$a'\in O$
with
![]() $M\models E(a',b_i,1)\land \lnot E(a',b_i,0)$
for all
$M\models E(a',b_i,1)\land \lnot E(a',b_i,0)$
for all
![]() $i<\omega $
. Now the map
$i<\omega $
. Now the map
![]() $f_i\colon \operatorname {acl}(a'b_i)\to \operatorname {acl}(ab)$
which swaps the elements of C and maps
$f_i\colon \operatorname {acl}(a'b_i)\to \operatorname {acl}(ab)$
which swaps the elements of C and maps
![]() $a'$
to a and
$a'$
to a and
![]() $b_i$
to b is an isomorphism of
$b_i$
to b is an isomorphism of
![]() $\mathcal L$
-substructures of M, so
$\mathcal L$
-substructures of M, so
![]() $a'b_i\equiv ab$
for all
$a'b_i\equiv ab$
for all
![]() $i<\omega $
by
$i<\omega $
by
![]() $(iv)$
above.
$(iv)$
above.
It remains to show ![]() . Note that
. Note that
![]() $\operatorname {acl}(\varnothing ) = C$
, so
$\operatorname {acl}(\varnothing ) = C$
, so
![]() $\text {tp}(a/\operatorname {acl}(\varnothing )b)$
contains the formula
$\text {tp}(a/\operatorname {acl}(\varnothing )b)$
contains the formula
![]() $E(x,b,0)$
. It suffices to show that this formula divides over C.
$E(x,b,0)$
. It suffices to show that this formula divides over C.
By
![]() $(iv)$
above, all elements of G have the same type over C. Let
$(iv)$
above, all elements of G have the same type over C. Let
![]() $(b_i)_{i< \omega }$
be a sequence of elements of G such that for all
$(b_i)_{i< \omega }$
be a sequence of elements of G such that for all
![]() $i\neq j$
,
$i\neq j$
,
![]() $R(b_i,b_j,0)$
. Then the set
$R(b_i,b_j,0)$
. Then the set
![]() $\{E(x,b_i,0)\mid i< \omega \}$
is
$\{E(x,b_i,0)\mid i< \omega \}$
is
![]() $2$
-inconsistent, which witnesses dividing.
$2$
-inconsistent, which witnesses dividing.
In the introduction we also claimed that all sets are extension bases in
![]() $T_{\mathsf {OG}}$
. This will be deduced from our general analysis of free amalgamation theories in Section 4 (see Corollary 4.10). Therefore
$T_{\mathsf {OG}}$
. This will be deduced from our general analysis of free amalgamation theories in Section 4 (see Corollary 4.10). Therefore
![]() $T_{\mathsf {OG}}$
is a second example demonstrating a negative answer to [Reference Adler3, Question A.1] (in addition to the example in Section 3.2).
$T_{\mathsf {OG}}$
is a second example demonstrating a negative answer to [Reference Adler3, Question A.1] (in addition to the example in Section 3.2).
4. Free amalgamation theories
In this section, we show that if T is a free amalgamation theory (as defined in [Reference Conant7]) with disintegrated algebraic closure, then forking and dividing are the same for complete types over algebraically closed sets. This proof is from an unpublished research note by the authors, written in May 2017. In the original note, we in fact claimed that this result holds for complete types over any set. However, our argument was flawed because we used [Reference Adler3, Remark 5.4(3)] to reduce to algebraically closed sets. In fact, the stronger claim fails since the theory
![]() $T_{\mathsf {OG}}$
from Section 3.3 is a free amalgamation theory with disintegrated algebraic closure (see Proposition 4.9).
$T_{\mathsf {OG}}$
from Section 3.3 is a free amalgamation theory with disintegrated algebraic closure (see Proposition 4.9).
Let T be a complete first-order theory with monster model
![]() $\mathbb M$
. For convenience, and to follow the conventions of [Reference Conant7], we will call a subset
$\mathbb M$
. For convenience, and to follow the conventions of [Reference Conant7], we will call a subset
![]() $A\subset \mathbb M$
closed if
$A\subset \mathbb M$
closed if
![]() $A=\operatorname {acl}(A)$
.
$A=\operatorname {acl}(A)$
.
Definition 4.1. T is a free amalgamation theory if there is an invariant ternary relation ![]() on small subsets of
on small subsets of
![]() $\mathbb M$
satisfying monotonicity and the following axioms:
$\mathbb M$
satisfying monotonicity and the following axioms:
-
(i) (Symmetry) For all
 $A,B,C$
, if
$A,B,C$
, if  then
then  .
. -
(ii) (Full transitivity) For all A and
 $D\subseteq C\subseteq B$
,
$D\subseteq C\subseteq B$
,  if and only if
if and only if  and
and  .
. -
(iii) (Full existence over closed sets) For all
 $B,C\subset \mathbb M$
and tuples
$B,C\subset \mathbb M$
and tuples
 $a\in \mathbb M$
, if C is closed then there is
$a\in \mathbb M$
, if C is closed then there is
 $a'\equiv _C a$
such that
$a'\equiv _C a$
such that  .
. -
(iv) (Stationarity over closed sets) For all closed
 $C\subset \mathbb M$
and closed tuples
$C\subset \mathbb M$
and closed tuples
 $a,a',b\in \mathbb M$
, with
$a,a',b\in \mathbb M$
, with
 $C\subseteq a\cap b$
, if
$C\subseteq a\cap b$
, if  ,
,  , and
, and
 $a'\equiv _C a$
, then
$a'\equiv _C a$
, then
 $ab\equiv _C a'b$
.
$ab\equiv _C a'b$
. -
(v) (Freedom) For all
 $A,B,C,D$
, if
$A,B,C,D$
, if  and
and
 $C\cap AB\subseteq D\subseteq C$
, then
$C\cap AB\subseteq D\subseteq C$
, then  .
. -
(vi) (Closure) For all closed
 $A,B,C$
, if
$A,B,C$
, if
 $C\subseteq A\cap B$
and
$C\subseteq A\cap B$
and  then
then
 $AB$
is closed.
$AB$
is closed.
We will ultimately focus on the case when T has disintegrated algebraic closure, which is to say that the algebraic closure of any set
![]() $A\subset \mathbb M$
is the union of the algebraic closures of singleton elements in A. This is equivalent to the property that
$A\subset \mathbb M$
is the union of the algebraic closures of singleton elements in A. This is equivalent to the property that
![]() $AB$
is closed for any closed
$AB$
is closed for any closed
![]() $A,B\subset \mathbb M$
.
$A,B\subset \mathbb M$
.
Example 4.2. The following are examples of free amalgamation theories with disintegrated algebraic closure.
-
(1) Let
 $\mathcal L$
be a finite relational language and let
$\mathcal L$
be a finite relational language and let
 $\mathcal K$
be a Fraïssé class of finite
$\mathcal K$
be a Fraïssé class of finite
 $\mathcal L$
-structures with free amalgamation. Let T be the complete theory of the Fraïssé limit of
$\mathcal L$
-structures with free amalgamation. Let T be the complete theory of the Fraïssé limit of
 $\mathcal K$
. Then T is a free amalgamation theory, and
$\mathcal K$
. Then T is a free amalgamation theory, and
 $\operatorname {acl}(A)=A$
for any
$\operatorname {acl}(A)=A$
for any
 $A\subset \mathbb M$
.
$A\subset \mathbb M$
. -
(2) Let
 $\mathcal L$
be the language of graphs and fix
$\mathcal L$
be the language of graphs and fix
 $n\geq 3$
. There is a unique (up to isomorphism) countable, universal, and existentially complete
$n\geq 3$
. There is a unique (up to isomorphism) countable, universal, and existentially complete
 $(K_n+K_3)$
-free graph (where
$(K_n+K_3)$
-free graph (where
 $K_n+K_3$
denotes the free amalgamation of
$K_n+K_3$
denotes the free amalgamation of
 $K_n$
and
$K_n$
and
 $K_3$
over a single vertex). If T is the complete theory of this graph, then T is a free amalgamation theory with disintegrated algebraic closure.
$K_3$
over a single vertex). If T is the complete theory of this graph, then T is a free amalgamation theory with disintegrated algebraic closure.
In both cases, the desired ternary relation ![]() is free amalgamation of relational structures: given
is free amalgamation of relational structures: given
![]() $A,B,C\subset \mathbb M$
,
$A,B,C\subset \mathbb M$
, ![]() if and only if
if and only if
![]() $ABC$
is the free amalgam of
$ABC$
is the free amalgam of
![]() $AC$
and
$AC$
and
![]() $BC$
over C. The verification of the axioms of Definition 4.1 for these examples is sketched in [Reference Conant7]. In the first case, all axioms are immediate from classical Fraïssé theory (see, e.g., [Reference Hodges16]). For the second case, the axioms rely on work of Cherlin, Shelah, and Shi [Reference Cherlin, Shelah and Shi5], and Patel [Reference Patel22].
$BC$
over C. The verification of the axioms of Definition 4.1 for these examples is sketched in [Reference Conant7]. In the first case, all axioms are immediate from classical Fraïssé theory (see, e.g., [Reference Hodges16]). For the second case, the axioms rely on work of Cherlin, Shelah, and Shi [Reference Cherlin, Shelah and Shi5], and Patel [Reference Patel22].
Recall our goal is to show that if T is a free amalgamation theory with disintegrated algebraic closure, then forking and dividing are the same for complete types over algebraically closed sets. Our proof strategy will follow that of [Reference Conant8], where this result is shown for the special case that T is the theory of the generic
![]() $K_n$
-free graph. In particular, we will first prove a “mixed transitivity” lemma involving dividing independence and the ternary relation
$K_n$
-free graph. In particular, we will first prove a “mixed transitivity” lemma involving dividing independence and the ternary relation ![]() in Definition 4.1. This general strategy is also used in [Reference Conant and Kruckman10, Reference d’Elbée12, Reference Kruckman and Ramsey20], where the equivalence of forking and dividing for complete types (over algebraically closed sets) is established via a mixed transitivity lemma involving a stationary independence relation.
in Definition 4.1. This general strategy is also used in [Reference Conant and Kruckman10, Reference d’Elbée12, Reference Kruckman and Ramsey20], where the equivalence of forking and dividing for complete types (over algebraically closed sets) is established via a mixed transitivity lemma involving a stationary independence relation.
Lemma 4.3. Let T be a free amalgamation theory with disintegrated algebraic closure. Suppose
![]() $A,B,C,D\subset \mathbb M$
are such that
$A,B,C,D\subset \mathbb M$
are such that
![]() $D\subseteq C\subseteq B$
and
$D\subseteq C\subseteq B$
and
![]() $C,D$
are closed. Then
$C,D$
are closed. Then
Proof Assume ![]() and
and ![]() . Enumerate
. Enumerate
![]() $B=b=(b_i)_{i\in I}$
. Assume
$B=b=(b_i)_{i\in I}$
. Assume
![]() $I_0\subseteq J$
are initial segments of I such that
$I_0\subseteq J$
are initial segments of I such that
![]() $D=(b_i)_{i\in I_0}$
and
$D=(b_i)_{i\in I_0}$
and
![]() $C=c=(b_i)_{i\in J}$
. Let
$C=c=(b_i)_{i\in J}$
. Let
![]() $(b^n)_{n<\omega }$
be a D-indiscernible sequence, with
$(b^n)_{n<\omega }$
be a D-indiscernible sequence, with
![]() $b^0=b$
. Let a enumerate A. We want to find
$b^0=b$
. Let a enumerate A. We want to find
![]() $a'$
such that
$a'$
such that
![]() $a'b^n\equiv _Dab$
for all
$a'b^n\equiv _Dab$
for all
![]() $n<\omega $
.
$n<\omega $
.
For
![]() $n<\omega $
, let
$n<\omega $
, let
![]() $c^n=(b^n_i)_{i\in J}$
, and note that
$c^n=(b^n_i)_{i\in J}$
, and note that
![]() $(c^n)_{n<\omega }$
is D-indiscernible with
$(c^n)_{n<\omega }$
is D-indiscernible with
![]() $c^0=c$
. There is some
$c^0=c$
. There is some
![]() $I_1$
such that
$I_1$
such that
![]() $I_0\subseteq I_1\subseteq J$
and, for all
$I_0\subseteq I_1\subseteq J$
and, for all
![]() $m< n<\omega $
and
$m< n<\omega $
and
![]() $i\in J$
,
$i\in J$
,
![]() $b^m_i=b^n_i$
if and only if
$b^m_i=b^n_i$
if and only if
![]() $i\in I_1$
. Set
$i\in I_1$
. Set
![]() $D'=(b_i)_{i\in I_1}$
, so
$D'=(b_i)_{i\in I_1}$
, so
![]() $D\subseteq D'\subseteq C$
, and by base monotonicity for
$D\subseteq D'\subseteq C$
, and by base monotonicity for ![]() , we have
, we have ![]() . Note also that
. Note also that
![]() $(b^n)_{n<\omega }$
and
$(b^n)_{n<\omega }$
and
![]() $(c^n)_{n<\omega }$
are each
$(c^n)_{n<\omega }$
are each
![]() $D'$
-indiscernible. We claim
$D'$
-indiscernible. We claim
![]() $D'$
is closed so that we may assume without loss of generality that
$D'$
is closed so that we may assume without loss of generality that
![]() $I_1=I_0$
and
$I_1=I_0$
and
![]() $D'=D$
.
$D'=D$
.
To show
![]() $D'$
is closed, fix
$D'$
is closed, fix
![]() $d\in \operatorname {acl}(D')$
. Since C is closed,
$d\in \operatorname {acl}(D')$
. Since C is closed,
![]() $d = b_{j_0}$
for some
$d = b_{j_0}$
for some
![]() $j_0\in J$
. Let
$j_0\in J$
. Let
![]() $j_0<\dots <j_{k-1}$
be the indices of the finitely many conjugates of
$j_0<\dots <j_{k-1}$
be the indices of the finitely many conjugates of
![]() $b_{j_0}$
over
$b_{j_0}$
over
![]() $D'$
. For every
$D'$
. For every
![]() $n\in \omega $
, there is some permutation
$n\in \omega $
, there is some permutation
![]() $\sigma _n\in S_k$
such that
$\sigma _n\in S_k$
such that
![]() $b^n_{j_i} = b_{j_{\sigma _n(i)}}$
for all
$b^n_{j_i} = b_{j_{\sigma _n(i)}}$
for all
![]() $i<k$
. By Pigeonhole, there exist
$i<k$
. By Pigeonhole, there exist
![]() $n<m$
such that
$n<m$
such that
![]() $\sigma _n = \sigma _m$
. Then
$\sigma _n = \sigma _m$
. Then
![]() $b^n_{j_i} = b^m_{j_i}$
for all
$b^n_{j_i} = b^m_{j_i}$
for all
![]() $i<k$
, so by indiscernibility
$i<k$
, so by indiscernibility
![]() $b^{n'}_{j_i} = b^n_{j_i}$
for all
$b^{n'}_{j_i} = b^n_{j_i}$
for all
![]() $n<n'$
, and hence
$n<n'$
, and hence
![]() $j_i\in I_1$
for all
$j_i\in I_1$
for all
![]() $i<k$
. In particular,
$i<k$
. In particular,
![]() $d = b_{j_0}\in D'$
.
$d = b_{j_0}\in D'$
.
Since ![]() , there is
, there is
![]() $a_*$
such that
$a_*$
such that
![]() $a_*c^n\equiv _D ac$
for all
$a_*c^n\equiv _D ac$
for all
![]() $n<\omega $
. Set
$n<\omega $
. Set
![]() $C_*=\operatorname {acl}(c^{<\omega })$
. Let e enumerate
$C_*=\operatorname {acl}(c^{<\omega })$
. Let e enumerate
![]() $\operatorname {acl}(a_*C_*)$
. By full existence for
$\operatorname {acl}(a_*C_*)$
. By full existence for ![]() , there is
, there is
![]() $e'\equiv _{C_*} e$
such that
$e'\equiv _{C_*} e$
such that ![]() . Note that there is some
. Note that there is some
![]() $a'\equiv _{C_*}a_*$
such that
$a'\equiv _{C_*}a_*$
such that
![]() $e'$
enumerates
$e'$
enumerates
![]() $\operatorname {acl}(a'C_*)$
. So we have
$\operatorname {acl}(a'C_*)$
. So we have ![]() . For each
. For each
![]() $n<\omega $
, we have
$n<\omega $
, we have
![]() $a'c^n\equiv _Da_*c^n\equiv _Dac$
. By monotonicity,
$a'c^n\equiv _Da_*c^n\equiv _Dac$
. By monotonicity, ![]() for all
for all
![]() $n<\omega $
.
$n<\omega $
.
Claim. For any
![]() $n<\omega $
,
$n<\omega $
,
![]() $C^*\cap \operatorname {acl}(a'c^n)b^n=c^n$
.
$C^*\cap \operatorname {acl}(a'c^n)b^n=c^n$
.
Proof Since algebraic closure in T is disintegrated, we have
![]() $\operatorname {acl}(a'c^n)=\operatorname {acl}(a')c^n$
and
$\operatorname {acl}(a'c^n)=\operatorname {acl}(a')c^n$
and
![]() $C^*=c^{<\omega }$
. So it suffices to show
$C^*=c^{<\omega }$
. So it suffices to show
![]() $c^{<\omega }\cap \operatorname {acl}(a')b^n=c^n$
. Fix some
$c^{<\omega }\cap \operatorname {acl}(a')b^n=c^n$
. Fix some
![]() $x\in c^{<\omega }\cap \operatorname {acl}(a')b^n$
. There is
$x\in c^{<\omega }\cap \operatorname {acl}(a')b^n$
. There is
![]() $m<\omega $
and
$m<\omega $
and
![]() $i\in J$
such that
$i\in J$
such that
![]() $x=b^m_i$
. Suppose first that
$x=b^m_i$
. Suppose first that
![]() $x\in \operatorname {acl}(a')$
. Then
$x\in \operatorname {acl}(a')$
. Then
![]() $b^m_i\in \operatorname {acl}(a')\cap c^m$
, which means
$b^m_i\in \operatorname {acl}(a')\cap c^m$
, which means
![]() $b_i\in \operatorname {acl}(a)\cap c$
. Since
$b_i\in \operatorname {acl}(a)\cap c$
. Since ![]() , we have
, we have
![]() $\operatorname {acl}(a)\cap c\subseteq D$
, and so
$\operatorname {acl}(a)\cap c\subseteq D$
, and so
![]() $i\in I_0$
. Thus
$i\in I_0$
. Thus
![]() $b^m_i=b^n_i\in c^n$
. Finally, suppose
$b^m_i=b^n_i\in c^n$
. Finally, suppose
![]() $x\in b^n$
. There is
$x\in b^n$
. There is
![]() $j\in I$
such that
$j\in I$
such that
![]() $b^m_i=b^n_j$
. It follows that
$b^m_i=b^n_j$
. It follows that
![]() $b^m_i=b^n_i$
(if
$b^m_i=b^n_i$
(if
![]() $m=n$
this is trivial, and if
$m=n$
this is trivial, and if
![]() $m\neq n$
use
$m\neq n$
use
![]() $b^m_i=b^n_j$
and indiscernibility). So
$b^m_i=b^n_j$
and indiscernibility). So
![]() $x=b^n_i\in c^n$
.
$x=b^n_i\in c^n$
.
![]() $\dashv _{\text {claim}}$
$\dashv _{\text {claim}}$
To finish the proof, we show
![]() $a'b^n\equiv _D ab$
for all
$a'b^n\equiv _D ab$
for all
![]() $n<\omega $
. So fix
$n<\omega $
. So fix
![]() $n<\omega $
, and let
$n<\omega $
, and let
![]() $\sigma \in \operatorname {Aut}(\mathbb M/D)$
be such that
$\sigma \in \operatorname {Aut}(\mathbb M/D)$
be such that
![]() $\sigma (b^n)=b$
(note that
$\sigma (b^n)=b$
(note that
![]() $\sigma (c^n)=c$
). By the claim and freedom, we have
$\sigma (c^n)=c$
). By the claim and freedom, we have ![]() . So
. So ![]() by invariance, and since
by invariance, and since
![]() $\sigma (\operatorname {acl}(a'c^n))=\operatorname {acl}(\sigma (a')c)$
. Also, we have
$\sigma (\operatorname {acl}(a'c^n))=\operatorname {acl}(\sigma (a')c)$
. Also, we have
![]() $\sigma (a')c\equiv _D a'c^n\equiv _D ac$
, and so
$\sigma (a')c\equiv _D a'c^n\equiv _D ac$
, and so
![]() $\sigma (a')c\equiv _c ac$
. Therefore
$\sigma (a')c\equiv _c ac$
. Therefore
![]() $\operatorname {acl}(\sigma (a')c)\equiv _c \operatorname {acl}(ac)$
. So we may fix tuples e and
$\operatorname {acl}(\sigma (a')c)\equiv _c \operatorname {acl}(ac)$
. So we may fix tuples e and
![]() $e'$
such that
$e'$
such that
![]() $\operatorname {acl}(ac)=ace$
,
$\operatorname {acl}(ac)=ace$
,
![]() $\operatorname {acl}(\sigma (a')c)=\sigma (a')ce'$
, and
$\operatorname {acl}(\sigma (a')c)=\sigma (a')ce'$
, and
![]() $ace\equiv _c \sigma (a')ce'$
. We have
$ace\equiv _c \sigma (a')ce'$
. We have ![]() and, by assumption,
and, by assumption, ![]() . Since
. Since
![]() $c\subseteq ace\cap b$
, we may apply stationarity to conclude
$c\subseteq ace\cap b$
, we may apply stationarity to conclude
![]() $aceb\equiv _c \sigma (a')ce' b$
. In particular,
$aceb\equiv _c \sigma (a')ce' b$
. In particular,
![]() $a'b^n\equiv _D \sigma (a')b\equiv _D ab$
.
$a'b^n\equiv _D \sigma (a')b\equiv _D ab$
.
Remark 4.4. Suppose T is a free amalgamation theory, witnessed by ![]() . Given closed
. Given closed
![]() $A,B,C\subset \mathbb M$
, with
$A,B,C\subset \mathbb M$
, with
![]() $C\subseteq A\cap B$
, if
$C\subseteq A\cap B$
, if ![]() then
then ![]() by [Reference Conant7, Lemma 7.15]. Therefore Lemma 4.3 can be seen as a weakening of transitivity for
by [Reference Conant7, Lemma 7.15]. Therefore Lemma 4.3 can be seen as a weakening of transitivity for ![]() . It is worth noting that many examples of such theories are not simple (e.g., the theory of the generic
. It is worth noting that many examples of such theories are not simple (e.g., the theory of the generic
![]() $K_n$
-free graph for
$K_n$
-free graph for
![]() $n\geq 3$
), and hence
$n\geq 3$
), and hence ![]() need not be transitive.
need not be transitive.
We now prove the main result.
Theorem 4.5. Let T be a free amalgamation theory with disintegrated algebraic closure. Then for any
![]() $A,B,C\subset \mathbb M$
,
$A,B,C\subset \mathbb M$
,
Proof First recall that in any theory we have ![]() . So conversely, suppose
. So conversely, suppose ![]() . We want to show
. We want to show ![]() . By Proposition 2.12, it suffices to show
. By Proposition 2.12, it suffices to show ![]() . We have
. We have ![]() by base monotonicity for
by base monotonicity for ![]() . So, altogether, we may assume without loss of generality that
. So, altogether, we may assume without loss of generality that
![]() $B,C$
are closed and
$B,C$
are closed and
![]() $C\subseteq B$
. To show
$C\subseteq B$
. To show ![]() , it suffices to fix
, it suffices to fix
![]() $\hat {B}\supseteq B$
and find
$\hat {B}\supseteq B$
and find
![]() $A'\equiv _{B}A$
such that
$A'\equiv _{B}A$
such that ![]() .
.
Let ![]() witness that T is a free amalgamation theory. By full existence there is
witness that T is a free amalgamation theory. By full existence there is
![]() $A'$
such that
$A'$
such that
![]() $A'\equiv _B A$
and
$A'\equiv _B A$
and ![]() . By invariance of
. By invariance of ![]() , we have
, we have ![]() . By Lemma 4.3,
. By Lemma 4.3, ![]() , as desired.
, as desired.
Remark 4.6. Given
![]() $n\geq 3$
, let
$n\geq 3$
, let
![]() $T_n$
be the theory of the generic
$T_n$
be the theory of the generic
![]() $K_n$
-free graph. In [Reference Conant8],
$K_n$
-free graph. In [Reference Conant8], ![]() is characterized for
is characterized for
![]() $T_n$
by purely combinatorial properties of graphs. It would be interesting to give similar descriptions of
$T_n$
by purely combinatorial properties of graphs. It would be interesting to give similar descriptions of ![]() for other theories listed in Example 4.2.
for other theories listed in Example 4.2.
Question 4.7. Does Theorem 4.5 hold without the assumption of disintegrated algebraic closure, or under the weaker assumption that algebraic closure is modular?
A possible lead toward the previous question could be recent work of Mutchnik [Reference Mutchnik21] which, among other things, studies a generalization of the class of free amalgamation theories.
Theorem 4.5 and Remark 2.10 together yield the following conclusion.
Corollary 4.8. If T is a free amalgamation theory with disintegrated algebraic closure then all sets are extension bases for nonforking.
Finally we revisit the theory
![]() $T_{\mathsf {OG}}$
from Section 3.3.
$T_{\mathsf {OG}}$
from Section 3.3.
Proposition 4.9.
![]() $T_{\mathsf {OG}}$
is a free amalgamation theory with disintegrated algebraic closure.
$T_{\mathsf {OG}}$
is a free amalgamation theory with disintegrated algebraic closure.
Proof If
![]() $A\subset \mathbb M$
then
$A\subset \mathbb M$
then
![]() $\operatorname {acl}(A)=A\cup \{0,1\}$
. Therefore algebraic closure is disintegrated. Let
$\operatorname {acl}(A)=A\cup \{0,1\}$
. Therefore algebraic closure is disintegrated. Let ![]() denote the usual free amalgamation of relational structures. Then we have invariance, monotonicity, symmetry, full transitivity, and freedom by the standard proofs (see the discussion in [Reference Conant7, Example 3.2]). Full existence over closed sets follows from free amalgamation in the class
denote the usual free amalgamation of relational structures. Then we have invariance, monotonicity, symmetry, full transitivity, and freedom by the standard proofs (see the discussion in [Reference Conant7, Example 3.2]). Full existence over closed sets follows from free amalgamation in the class
![]() $\mathcal K$
, and stationarity over closed sets follows from the description of algebraic closure and “almost quantifier elimination”. Finally, the closure axiom is trivial since algebraic closure is disintegrated.
$\mathcal K$
, and stationarity over closed sets follows from the description of algebraic closure and “almost quantifier elimination”. Finally, the closure axiom is trivial since algebraic closure is disintegrated.
Corollary 4.10. In
![]() $T_{\mathsf {OG}}$
,
$T_{\mathsf {OG}}$
, ![]() satisfies full existence, but
satisfies full existence, but ![]() .
.
5. Corrections to literature
The purpose of this section is to collect and discuss some arguments in the literature which rely on the incorrect statements made in [Reference Adler3, Remark 5.4]. We do not claim that this list is exhaustive.
5.1. The model completion of the empty theory
Let
![]() $\mathcal L$
be an arbitrary language and let
$\mathcal L$
be an arbitrary language and let
![]() $T^{\varnothing }_{\mathcal L}$
be the model completion of the empty
$T^{\varnothing }_{\mathcal L}$
be the model completion of the empty
![]() $\mathcal L$
-theory. In [Reference Kruckman and Ramsey20, Proposition 3.17], it is shown that
$\mathcal L$
-theory. In [Reference Kruckman and Ramsey20, Proposition 3.17], it is shown that ![]() coincides with
coincides with ![]() in (any completion of)
in (any completion of)
![]() $T^{\varnothing }_{\mathcal L}$
. The proof quotes [Reference Adler3, Remark 5.4(4)] for
$T^{\varnothing }_{\mathcal L}$
. The proof quotes [Reference Adler3, Remark 5.4(4)] for ![]() , which is valid in this case since algebraic closure and definable closure coincide (see [Reference Kruckman and Ramsey20, Corollary 3.11]).
, which is valid in this case since algebraic closure and definable closure coincide (see [Reference Kruckman and Ramsey20, Corollary 3.11]).
5.2. Simple free amalgamation theories
In [Reference Conant7], preservation of algebraic closure for ![]() is stated as Fact 7.4 and used in the proof that a free amalgamation theory is simple if and only if it is
is stated as Fact 7.4 and used in the proof that a free amalgamation theory is simple if and only if it is
![]() $\mathrm {NTP}_2$
, as well as the corresponding analysis of forking independence in this case. However, it turns out that the full power of Fact 7.4 is only required in the context of simplicity, and the remaining applications actually use weaker statements (which are true). See the corrigenda to [Reference Conant7] for further details (available in the most recent arXiv version of [Reference Conant7]).
$\mathrm {NTP}_2$
, as well as the corresponding analysis of forking independence in this case. However, it turns out that the full power of Fact 7.4 is only required in the context of simplicity, and the remaining applications actually use weaker statements (which are true). See the corrigenda to [Reference Conant7] for further details (available in the most recent arXiv version of [Reference Conant7]).
5.3. Generic incidence structures
Let
![]() $\mathcal L=\{P,L,I\}$
where P and L are unary relations (for “points” and “lines”) and I is a binary relation (for “incidences”). An incidence structure is an
$\mathcal L=\{P,L,I\}$
where P and L are unary relations (for “points” and “lines”) and I is a binary relation (for “incidences”). An incidence structure is an
![]() $\mathcal L$
-structure in which P and L partition the universe and
$\mathcal L$
-structure in which P and L partition the universe and
![]() $I\subseteq P\times L$
. In [Reference Conant and Kruckman10], we study the complete theory
$I\subseteq P\times L$
. In [Reference Conant and Kruckman10], we study the complete theory
![]() $T_{m,n}$
of existentially closed
$T_{m,n}$
of existentially closed
![]() $K_{m,n}$
-free incidence structures, where
$K_{m,n}$
-free incidence structures, where
![]() $m,n\geq 1$
. The special case
$m,n\geq 1$
. The special case
![]() $T_{2,2}$
can also be viewed as the theory of existentially closed projective planes. In the paper, we define a certain ternary relation
$T_{2,2}$
can also be viewed as the theory of existentially closed projective planes. In the paper, we define a certain ternary relation ![]() and use it to show that
and use it to show that
![]() $T_{m,n}$
is
$T_{m,n}$
is
![]() $\mathrm {NSOP}_1$
and that, over models,
$\mathrm {NSOP}_1$
and that, over models, ![]() coincides with Kim-independence (see [Reference Conant and Kruckman10, Theorem 4.11]). We later claim in Corollaries 4.14 and 4.24 of [Reference Conant and Kruckman10] that
coincides with Kim-independence (see [Reference Conant and Kruckman10, Theorem 4.11]). We later claim in Corollaries 4.14 and 4.24 of [Reference Conant and Kruckman10] that ![]() and
and ![]() are the same, and coincide with “forcing base monotonicity” on
are the same, and coincide with “forcing base monotonicity” on ![]() (in the sense of [Reference Adler3]). However, our arguments tacitly use [Reference Adler3, Remark 5.4(3)] in a few places and, as we will show below, it is in fact not true that
(in the sense of [Reference Adler3]). However, our arguments tacitly use [Reference Adler3, Remark 5.4(3)] in a few places and, as we will show below, it is in fact not true that ![]() has algebraic extension in
has algebraic extension in
![]() $T_{m,n}$
for all
$T_{m,n}$
for all
![]() $m,n\geq 1$
.
$m,n\geq 1$
.
Before getting deeper into these issues, we first note that when
![]() $m=n=2$
(which is the main case of interest), our proofs are valid because algebraic closure coincides with definable closure in this case (see [Reference Conant and Kruckman10, Proposition 2.14] and the closing remarks of [Reference Conant and Kruckman10, Section 2]). Our proofs are also valid when
$m=n=2$
(which is the main case of interest), our proofs are valid because algebraic closure coincides with definable closure in this case (see [Reference Conant and Kruckman10, Proposition 2.14] and the closing remarks of [Reference Conant and Kruckman10, Section 2]). Our proofs are also valid when
![]() $\min \{m,n\}=1$
because in this case
$\min \{m,n\}=1$
because in this case
![]() $T_{m,n}$
is stable (see [Reference Conant and Kruckman10, Section 4.5]).
$T_{m,n}$
is stable (see [Reference Conant and Kruckman10, Section 4.5]).
For general
![]() $m,n$
, we will show that the above claims about
$m,n$
, we will show that the above claims about ![]() are not always true. However, it is easy to see that our proofs work with
are not always true. However, it is easy to see that our proofs work with ![]() replaced by
replaced by ![]() . Thus we have that for
. Thus we have that for
![]() $A,B,C\subset \mathbb M\models T_{m,n}$
,
$A,B,C\subset \mathbb M\models T_{m,n}$
,
Part of the proof uses [Reference Conant and Kruckman10, Lemma 4.23], which gives a mixed transitivity statement for ![]() using a stationary independence relation (similar to Lemma 4.3). The proof tacitly assumes preservation of algebraic closure for
using a stationary independence relation (similar to Lemma 4.3). The proof tacitly assumes preservation of algebraic closure for ![]() , and so here one needs to also replace
, and so here one needs to also replace ![]() with
with ![]() to obtain a correct statement.
to obtain a correct statement.
We also note that [Reference Conant and Kruckman10, Proposition 4.22] includes the claim that ![]() implies
implies ![]() . While this is presented as an immediate consequence of [Reference Conant and Kruckman10, Corollary 4.14] (which is false as stated), one can instead obtain this claim directly from Lemma 4.8 and Remark 4.12 of [Reference Conant and Kruckman10], which are unaffected by the issues with [Reference Adler3, Remark 5.4].
. While this is presented as an immediate consequence of [Reference Conant and Kruckman10, Corollary 4.14] (which is false as stated), one can instead obtain this claim directly from Lemma 4.8 and Remark 4.12 of [Reference Conant and Kruckman10], which are unaffected by the issues with [Reference Adler3, Remark 5.4].
Finally, we describe a counterexample to [Reference Conant and Kruckman10, Corollary 4.14], which also gives an instance where ![]() and
and ![]() disagree. We will assume some familiarity with general setup of [Reference Conant and Kruckman10]. Work in
disagree. We will assume some familiarity with general setup of [Reference Conant and Kruckman10]. Work in
![]() $T_{4,2}$
, so any four points are incident a unique line, and any two lines have exactly three points incident to them. Consider the incidence structure
$T_{4,2}$
, so any four points are incident a unique line, and any two lines have exactly three points incident to them. Consider the incidence structure
![]() $(P,L;I)$
where
$(P,L;I)$
where
![]() $P=\{a_0,a_1,a_2,d_0,d_1,d_2\}$
,
$P=\{a_0,a_1,a_2,d_0,d_1,d_2\}$
,
![]() $L=\{b_0,b_1,e\}$
, and I consists of
$L=\{b_0,b_1,e\}$
, and I consists of
![]() $(d_0,e)$
,
$(d_0,e)$
,
![]() $(d_1,e)$
,
$(d_1,e)$
,
![]() $(d_i,b_j)$
for all i and j, and
$(d_i,b_j)$
for all i and j, and
![]() $(a_i,e)$
for all i. Then
$(a_i,e)$
for all i. Then
![]() $(P,L;I)$
is
$(P,L;I)$
is
![]() $K_{4,2}$
-free, so we can freely complete it and embed it in the monster model of
$K_{4,2}$
-free, so we can freely complete it and embed it in the monster model of
![]() $T_{4,2}$
. Note that
$T_{4,2}$
. Note that
![]() $\{d_0, d_1, d_2\}$
is the unique set of three points incident to the lines
$\{d_0, d_1, d_2\}$
is the unique set of three points incident to the lines
![]() $b_0$
and
$b_0$
and
![]() $b_1$
, hence
$b_1$
, hence
![]() $d_0,d_1,d_2\in \operatorname {acl}(b_0,b_1)$
. One can then show that
$d_0,d_1,d_2\in \operatorname {acl}(b_0,b_1)$
. One can then show that ![]() and
and ![]() , which altogether refutes [Reference Conant and Kruckman10, Corollary 4.14]. Moreover, since
, which altogether refutes [Reference Conant and Kruckman10, Corollary 4.14]. Moreover, since ![]() implies
implies ![]() (and satisfies base monotonicity and extension), we also have
(and satisfies base monotonicity and extension), we also have ![]() and thus a counterexample to [Reference Conant and Kruckman10, Corollary 4.24]. We leave the verification of these details to the reader. When checking
and thus a counterexample to [Reference Conant and Kruckman10, Corollary 4.24]. We leave the verification of these details to the reader. When checking ![]() , the key point is that every indiscernible sequence of
, the key point is that every indiscernible sequence of
![]() $3$
-tuples is either constant in at least two coordinates or non-constant in at least two coordinates. This explains the need for
$3$
-tuples is either constant in at least two coordinates or non-constant in at least two coordinates. This explains the need for
![]() $m=4$
in order to work with
$m=4$
in order to work with
![]() $3$
-tuples.
$3$
-tuples.
Recall that
![]() $T_{4,2}$
is
$T_{4,2}$
is
![]() $\mathrm {NSOP}_1$
and thus, in addition to the theory
$\mathrm {NSOP}_1$
and thus, in addition to the theory
![]() $T^{\mathrm {eq}}_f$
from Section 3.2, this gives another counterexample to the question from [Reference d’Elbée12] discussed in the introduction. Note also that one can adjust the above configuration to obtain
$T^{\mathrm {eq}}_f$
from Section 3.2, this gives another counterexample to the question from [Reference d’Elbée12] discussed in the introduction. Note also that one can adjust the above configuration to obtain ![]() for any small model M by starting with a copy of
for any small model M by starting with a copy of
![]() $(P,L;I)$
with no incidences to M (and taking the free completion with M).
$(P,L;I)$
with no incidences to M (and taking the free completion with M).
For
![]() $m\geq 4$
and
$m\geq 4$
and
![]() $n\geq 2$
, a similar configuration can be constructed in
$n\geq 2$
, a similar configuration can be constructed in
![]() $T_{m,n}$
using the interpretation of
$T_{m,n}$
using the interpretation of
![]() $T_{4,2}$
in
$T_{4,2}$
in
![]() $T_{m,n}$
described in [Reference Conant and Kruckman10, Lemma 3.2]. This leaves open the case of
$T_{m,n}$
described in [Reference Conant and Kruckman10, Lemma 3.2]. This leaves open the case of
![]() $T_{3,2}$
, which we will not pursue here.
$T_{3,2}$
, which we will not pursue here.
5.4. Algebraically closed fields with a generic additive subgroup
For a fixed
![]() $p>0$
, let ACFG denote the model companion of the theory of algebraically closed fields of characteristic p with a predicate G for an additive subgroup. It turns out that the study of this theory is affected by [Reference Adler3, Remark 5.4] in ways very similar to the theories
$p>0$
, let ACFG denote the model companion of the theory of algebraically closed fields of characteristic p with a predicate G for an additive subgroup. It turns out that the study of this theory is affected by [Reference Adler3, Remark 5.4] in ways very similar to the theories
![]() $T_{m,n}$
(discussed in the previous subsection). In particular, d’Elbée first showed in [Reference d’Elbée11] that (any completion of) ACFG is properly
$T_{m,n}$
(discussed in the previous subsection). In particular, d’Elbée first showed in [Reference d’Elbée11] that (any completion of) ACFG is properly
![]() $\mathrm {NSOP}_1$
, and then in a sequel paper [Reference d’Elbée12] it is asserted that
$\mathrm {NSOP}_1$
, and then in a sequel paper [Reference d’Elbée12] it is asserted that ![]() and
and ![]() are the same and coincide with forcing base monotonicity on Kim independence. However, some arguments in [Reference d’Elbée12] rely on [Reference Adler3, Remark 5.4]. Following discussions based on an early version of this paper, d’Elbée has constructed an example showing that, like in
are the same and coincide with forcing base monotonicity on Kim independence. However, some arguments in [Reference d’Elbée12] rely on [Reference Adler3, Remark 5.4]. Following discussions based on an early version of this paper, d’Elbée has constructed an example showing that, like in
![]() $T^{\mathrm {eq}}_f$
and
$T^{\mathrm {eq}}_f$
and
![]() $T_{4,2}$
,
$T_{4,2}$
, ![]() and
and ![]() need not coincide in ACFG, even over models. On the other hand, the arguments from [Reference d’Elbée12] work with
need not coincide in ACFG, even over models. On the other hand, the arguments from [Reference d’Elbée12] work with ![]() replaced by
replaced by ![]() . So it is still true that forking and dividing are the same for complete types over algebraically closed sets, and that
. So it is still true that forking and dividing are the same for complete types over algebraically closed sets, and that ![]() is the base monotonization of Kim independence (see [Reference d’Elbée14] for details).
is the base monotonization of Kim independence (see [Reference d’Elbée14] for details).
Acknowledgements
The authors thank Christian d’Elbée and Nick Ramsey for stimulating discussions, as well as the anonymous referee for their careful reading of the paper and helpful revisions. Conant was partially supported by NSF grant DMS-2204787.