Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hjorth, Greg
1996.
Some applications of illfoundedness.
Archive for Mathematical Logic,
Vol. 35,
Issue. 3,
p.
131.
Кановей, Владимир Григорьевич
and
Kanovei, Vladimir Grigor'evich
1996.
Топологии, порожденные эффективно суслинскими множествами, и их приложения в дескриптивной теории множеств.
Успехи математических наук,
Vol. 51,
Issue. 3,
p.
17.
Friedman, Sy
and
Velickovic, Boban
1997.
Nonstandard models and analytic equivalence relations.
Proceedings of the American Mathematical Society,
Vol. 125,
Issue. 6,
p.
1807.
Kanovei, Vladimir
1998.
Ulm Classification of Analytic Equivalence Relations in Generic Universes.
Mathematical Logic Quarterly,
Vol. 44,
Issue. 3,
p.
287.
Kanovei, Vladimir
2000.
Linearization of definable order relations.
Annals of Pure and Applied Logic,
Vol. 102,
Issue. 1-2,
p.
69.
Schlicht, Philipp
2014.
Thin equivalence relations and inner models.
Annals of Pure and Applied Logic,
Vol. 165,
Issue. 10,
p.
1577.
CHAN, WILLIAM
2017.
EQUIVALENCE RELATIONS WHICH ARE BOREL SOMEWHERE.
The Journal of Symbolic Logic,
Vol. 82,
Issue. 3,
p.
893.
Castiblanco, Fabiana
and
Schlicht, Philipp
2021.
Preserving levels of projective determinacy by tree forcings.
Annals of Pure and Applied Logic,
Vol. 172,
Issue. 4,
p.
102918.


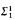 equivalence relation for which there does not exist a perfect set of inequivalent reals. If 0* exists or if
equivalence relation for which there does not exist a perfect set of inequivalent reals. If 0* exists or if 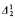 well-ordering of the equivalence classes.
well-ordering of the equivalence classes.