Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-22T20:21:42.905Z Has data issue: false hasContentIssue false
  • English
  • Français

There are reasonably nice logics

Published online by Cambridge University Press:  12 March 2014

Wilfrid Hodges  and
Saharon Shelah
Wilfrid Hodges
Affiliation:
School of Mathematical Sciences, Queen Mary and Westfield College, London E1 4NS, England
Saharon Shelah
Affiliation:
Department of Mathematics, The Hebrew University, Givat Ram, Jerusalem, Israel
Get access Rights & Permissions [Opens in a new window]

Extract

A well-known question of Feferman asks whether there is a logic which extends the logic 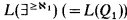, is ℵ0-compact and satisfies the interpolation theorem. (Cf. Makowsky [M] for background and terminology.)

The same question was open when ℵ1 in is replaced by any other uncountable cardinal κ. We shall show that when κ is an uncountable strongly compact cardinal and there is a strongly compact cardinal > κ, then there is such a logic. It is impossible to prove the existence of uncountable strongly compact cardinals in ZFC. However, the logic that we describe has a simple and natural definition, together with several other pleasant properties. For example it satisfies Robinson's lemma, PPP (pair preservation property, viz. the theory of the sum of two models is the sum of their theories), versions of the elementary chain lemma for chains of length < λ, and isomorphism of (suitable) ultralimits.

This logic is described in §2 below; we call it 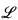1. It is not a new logic—it was introduced in [Sh, Part II, §3] as an example of a logic which has the amalgamation and joint embedding properties. See the transparent presentation in [M]. But we shall repeat all the definitions. In [HS] we presented a logic with some of the same properties as 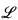1, also based on a strongly compact cardinal λ; but unlike 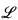1, it was not a sublogic of 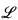λ,λ.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 56 , Issue 1 , March 1991 , pp. 300 - 322
Copyright
Copyright © Association for Symbolic Logic 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[A]Arrow, Kenneth J., A difficulty in the concept of social welfare, Journal of Political Economy, vol. 58 (1950), pp. 328–346.CrossRefGoogle Scholar
[B]Barwise, K. J., Some applications of Henkin quantifiers, Israel Journal of Mathematics, vol. 25 (1976), pp. 47–63.CrossRefGoogle Scholar
[BF]Barwise, J. and Feferman, S. (editors), Model-theoretic logics, Springer-Verlag, New York, 1985.Google Scholar
[CK]Chang, C. C. and Keisler, H. J., Model theory, North-Holland, Amsterdam, 1973.Google Scholar
[CP]Charretton, Christine and Pouzet, Maurice, Comparaison des structures engendrees par des chaînes, Proceedings of the Dietrichshagen Easter conference on model theory, Seminarbericht No. 49, Sektion Mathematik, Humboldt-University, Berlin, 1983, pp. 17–27.Google Scholar
[D]Dickmann, M. A., Larger infinitary languages, in [BF], pp. 317–363.CrossRefGoogle Scholar
[FV]Feferman, S. and Vaught, R. L., The first-order properties of algebraic systems, Fundamenta Mathematicae, vol. 47 (1959), pp. 57–103.CrossRefGoogle Scholar
[H]Hodges, Wilfrid, Some questions on the structure of models, D.Phil. Thesis, Oxford University, Oxford, 1969.Google Scholar
[HS]Hodges, Wilfrid and Shelah, Saharon, Infinite games and reduced products, Annals of Mathematical Logic, vol. 20 (1981), pp. 77–108.CrossRefGoogle Scholar
[K]Kaufmann, M., The quantifier “There exist uncountably many” and some of its relatives, in [BF], p. 123–176.CrossRefGoogle Scholar
[M]Makowsky, J. A., Compactness, embeddings and definability, in [BF], pp. 645–716.CrossRefGoogle Scholar
[MM]Magidor, M. and Malitz, J. J., Compact extensions of L(Q) (Part la), Annals of Mathematical Logic, vol. 11 (1977), pp. 217–261.CrossRefGoogle Scholar
[Sc]Schmerl, James H., An axiomatization for a class of two-cardinal models, this Journal, vol. 42 (1977), pp. 174–178.Google Scholar
[Sh]Shelah, Saharon, Remarks on abstract model theory, Annals of Pure and Applied Logic, vol. 29 (1985), pp. 255–288.CrossRefGoogle Scholar
[SSI]Shelah, Saharon and Steinhorn, Charles, The non-axiomatizability of by finitely many schemata, Notre Dame Journal of Formal Logic, vol. 31 (1990), pp. 1–13.Google Scholar
[SS2]Shelah, Saharon, On the non-axiomatizability of some logics by finitely many schemas, Notre Dame Journal of Formal Logic, vol. 27 (1986), pp. 1–11.CrossRefGoogle Scholar