Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-25T00:36:58.105Z Has data issue: false hasContentIssue false
  • English
  • Français

Theory of models with generalized atomic formulas

Published online by Cambridge University Press:  12 March 2014

H. Jerome Keisler
H. Jerome Keisler*
Affiliation:
California Institute of Technology
Get access Rights & Permissions [Opens in a new window]

Introduction

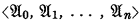We shall prove the following theorem, which gives a necessary and sufficient condition for an elementary class to be characterized by a set of sentences having a prescribed number of alternations of quantifiers. A finite sequence of relational systems is said to be a sandwich of order n if each 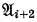is an elementary extension of 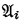(i ≦ n—2), and each 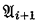is an extension of 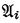(i ≦ n—2). If K is an elementary class, then the statements (i) and (ii) are equivalent for each fixed natural number n.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 25 , Issue 1 , March 1960 , pp. 1 - 26
Copyright
Copyright © Association for Symbolic Logic 1960

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Chang, C. C., On unions of chains of models, Proceedings of the American Mathematical Society, Vol. 10 (1959), pp. 120–127.CrossRefGoogle Scholar
[2]Frayne, T. E. and Scott, D. S., Model-theoretic properties of reduced products, American Mathematical Society notices, Vol. 5 (1958), Abstract 550–70.Google Scholar
[3]Gödel, K., Die Vollständigkeit der Axiome des logischen Funktionkalküls, Monatshefte für Mathematik und Physik, Vol. 37 (1930), pp. 349–360.CrossRefGoogle Scholar
[4]Henkin, L., The completeness of the first order functional calculus, this Journal, Vol. 14 (1949), pp. 433–454.Google Scholar
[5]Henkin, L., Some interconnections between modern algebra and mathematical logic, Transactions of the American Mathematical Society, Vol. 74 (1953), pp. 410–427.CrossRefGoogle Scholar
[6]Henkin, L., Two concepts from the theory of models, this Journal, Vol. 21 (1956), pp. 28–32.Google Scholar
[7]Keisler, H. J., The theory of models with generalized atomic formulas, I and II, American Mathematical Society notices, Vol. 5 (1958), Abstracts 550–14 and 550–31.Google Scholar
[8]Keisler, H. J., On unions of relational systems, American Mathematical Society notices Vol. 6 (1959), Abstract 556–14.Google Scholar
[9]Łoś, J. and Suszko, R., On the extending of models, (IV), Infinite sums of models, Fundamenta Mathematicae, Vol. 44 (1957), pp. 52–60.CrossRefGoogle Scholar
[10]Łoś, J., Sur les classes définissables, p. 107, in Mathematical interpretation of formal systerns, Amsterdam (North Holland Publishing Co.), 1955.Google Scholar
[11]Lyndon, R. C., Properties preserved under homomorphism, Pacific journal of mathematics, Vol. 9 (1959), pp. 143–154.CrossRefGoogle Scholar
[12]Robinson, A., On the metamathematics of algebra, Amsterdam (North Holland Publishing Co.), 1951.Google Scholar
[13]Robinson, A., Note on a problem of Henkin, this Journal, Vol. 21 (1956), pp. 33–35.Google Scholar
[14]Tarski, A., Contributions to the theory of models, Parts I and II, Indagationes mathematica, Vol. 16 (1954), pp. 572–588.CrossRefGoogle Scholar
[15]Tarski, A. and Vaught, R., Arithmetical extensions of relational systems, Compositie mathematica, Vol. 13 (1958), pp. 81–102.Google Scholar