Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Koiran, Pascal
Portier, Natacha
and
Villard, Gilles
2004.
A rank theorem for Vandermonde matrices.
Linear Algebra and its Applications,
Vol. 378,
Issue. ,
p.
99.
Baldwin, John T.
2004.
Notes on Quasiminimality and Excellence.
Bulletin of Symbolic Logic,
Vol. 10,
Issue. 3,
p.
334.
Peatfield, Nick
2006.
An Analytic Zariski Structure Over a Field.
Archive for Mathematical Logic,
Vol. 45,
Issue. 6,
p.
739.
Haskell, Deirdre
2012.
Model Theory of Analytic Functions: Some Historical Comments.
The Bulletin of Symbolic Logic,
Vol. 18,
Issue. 3,
p.
368.
Kirby, Jonathan
2013.
Finitely presented exponential fields.
Algebra & Number Theory,
Vol. 7,
Issue. 4,
p.
943.
Zilber, Boris
2017.
Logic Colloquium 2000.
p.
392.
Koiran, Pascal
2017.
Logic Colloquium '01.
p.
242.
Wilkie, Alex J.
2024.
Analytic continuation and Zilber’s quasiminimality
conjecture.
Model Theory,
Vol. 3,
Issue. 2,
p.
701.


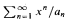 such the
such the 