Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-22T23:04:51.815Z Has data issue: false hasContentIssue false
  • English
  • Français

A theorem on the isomorphism property

Published online by Cambridge University Press:  12 March 2014

Renling Jin
Renling Jin*
Affiliation:
Department of Mathematics, University of California, Berkeley, CA 94720, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An 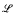-structure is called internally presented in a nonstandard universe if its base set and interpretation of every symbol in 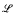are internal. A nonstandard universe is said to satisfy the κ-isomorphism property if for any two internally presented 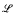-structures 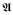and 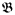, where 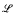has less than κ many symbols, 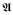is elementarily equivalent to 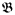implies that 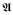is isomorphic to 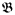. In this paper we prove that the ℵ1-isomorphism property is equivalent to the ℵ0-isomorphism property plus ℵ1-saturation.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 57 , Issue 3 , September 1992 , pp. 1011 - 1017
Copyright
Copyright © Association for Symbolic Logic 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[CK]Chang, Chen Chung and Keisler, H. Jerome, Model theory, North-Holland, Amsterdam, 1973; 3rd ed., 1990.Google Scholar
[H1]Henson, C. Ward, The isomorphism property in nonstandard analysis and its use in the theory of Banach space, this Journal, vol. 39 (1974), pp. 717–731.Google Scholar
[H2]Henson, C. Ward, When do two Banach spaces have isometrically isomorphic nonstandard hulls, Israel Journal of Mathematics, vol. 22 (1975), pp. 57–67.CrossRefGoogle Scholar
[H3]Henson, C. Ward, Nonstandard hulls of Banach spaces, Israel Journal of Mathematics, vol. 25 (1976), pp. 108–144.CrossRefGoogle Scholar
[H4]Henson, C. Ward, Private communication.Google Scholar
[J]Jin, Renling, The isomorphism property versus the special model axiom, this Journal, vol. 57 (1992), (to appear).Google Scholar
[R]Ross, David, “The special model axiom in nonstandard analysis, this Journal, vol. 55 (1990), pp. 1233–1242.Google Scholar