Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T11:04:37.340Z Has data issue: false hasContentIssue false
  • English
  • Français

A theorem on shortening the length of proof in formal systems of arithmetic

Published online by Cambridge University Press:  12 March 2014

Robert A. di Paola
Get access Rights & Permissions [Opens in a new window]

Extract

This note is concerned with an aspect of the length of proof of formulas 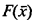in recursively enumerable theories T adequate for recursive arithmetic. In particular, we consider the relative length of proof of formulas 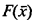in the theories T and T(S), where F represents an r.e. set A in T and T(S) is the theory obtained from T by adjunction, as a new axiom, of a sentence S undecidable in T.

Throughout the sequel T is a consistent, r.e. theory with standard formalization [7] in which all recursive functions of one variable are definable, and in which there is a binary formula x ≤ satisfying the well-known conditions [7]:

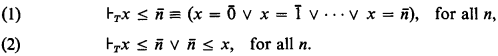
Here 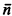is the constant term corresponding to the natural number n. Wn is the nth r.e. set in a standard enumeration of the r.e. sets. Also, we assume an a priori Gödel numbering of our formalism satisfying the usual conditions, so that all formulas are numbers ab initio.

In the more common applications of the theorem below, if F is a k-ary formula of T, 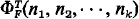is a natural number that measures in some way the length of the shortest proof of 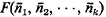in T.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 40 , Issue 3 , September 1975 , pp. 398 - 400
Copyright
Copyright © Association for Symbolic Logic 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Di Paola, R. A., Some properties of pseudo-complements of recursively enumerable sets, Transactions of the American Mathematical Society, vol. 121 (1966), pp. 296–308.CrossRefGoogle Scholar
[2]Di Paola, R. A., Some theorems on extensions of arithmetic, this Journal, vol. 32 (1967), pp. 180–189.Google Scholar
[3]Di Paola, R. A., On sets representable by the same formula in consistent, axiomatizable Rosser theories, Pacific Journal of Mathematics, vol. 18 (1966), pp. 455–456.CrossRefGoogle Scholar
[4]Ehrenfeucht, A. and Mycielski, J., Abbreviating proofs by adding new axioms, Bulletin of the American Mathematical Society, vol. 77 (1971), pp. 366–367.CrossRefGoogle Scholar
[5]Feferman, S., Arithmetization of metamathematics in a general setting, Fundamenta Mathematicae, vol. 49 (1960), pp. 35–92.CrossRefGoogle Scholar
[6]Godel, K., On the length of proofs, The undecidable (Davis, Martin, Editor), Raven Press, New York, 1965, pp. 82–83.Google Scholar
[7]Tarski, A., Mostowski, A. and Robinson, R. M., Undecidable theories, North-Holland, Amsterdam, 1953.Google Scholar