Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T12:22:51.717Z Has data issue: false hasContentIssue false
  • English
  • Français

Term extraction and Ramsey's theorem for pairs

Published online by Cambridge University Press:  12 March 2014

Alexander P. Kreuzer  and
Ulrich Kohlenbach
Alexander P. Kreuzer
Affiliation:
Technische Universität Darmstadt, Fachbereich Mathematik Schlossgartenstrasse 7, 64289 Darmstadt, Germany, E-mail: [email protected], E-mail: [email protected]
Ulrich Kohlenbach
Affiliation:
Technische Universität Darmstadt, Fachbereich Mathematik Schlossgartenstrasse 7, 64289 Darmstadt, Germany, E-mail: [email protected], E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we study with proof-theoretic methods the function(al)s provably recursive relative to Ramsey's theorem for pairs and the cohesive principle (COH).

Our main result on COH is that the type 2 functional provably recursive from 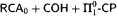are primitive recursive. This also provides a uniform method to extract bounds from proofs that use these principles. As a consequence we obtain a new proof of the fact that 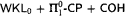is 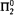-conservative over PRA.

Recent work of the first author showed that 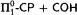is equivalent to a weak variant of the Bolzano-Weierstraß principle. This makes it possible to use our results to analyze not only combinatorial but also analytical proofs.

For Ramsey's theorem for pairs and two colors 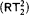we obtain the upper bounded that the type 2 functional provable recursive relative to 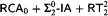are in T1. This is the fragment of Gödel's system T containing only type 1 recursion—roughly speaking it consists of functions of Ackermann type. With this we also obtain a uniform method for the extraction of T1-bounds from proofs that use 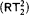. Moreover, this yields a new proof of the fact that 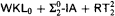is 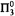-conservative over .

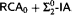The results are obtained in two steps: in the first step a term including Skolem functions for the above principles is extracted from a given proof. This is done using Gödel's functional interpretation. After this the term is normalized, such that only specific instances of the Skolem functions are used. In the second step this term is interpreted using 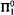-comprehension. The comprehension is then eliminated in favor of induction using either elimination of monotone Skolem functions (for COH) or Howard's ordinal analysis of bar recursion (for ).

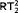Keywords

Ramsey's theoremcohesive principleproof miningfunctional interpretationconservation
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 77 , Issue 3 , September 2012 , pp. 853 - 895
Copyright
Copyright © Association for Symbolic Logic 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Avigad, Jeremy Notes on -conservativity, ω-submodels, and collection schema. Technical report, Carnegie Mellon Department of Philosophy, 2002.Google Scholar
[2] Avigad, Jeremy, Forcing in proof theory, The Bulletin of Symbolic Logic, vol. 10 (2004), no. 3, pp. 305–333.Google Scholar
[3] Avigad, Jeremy and Feferman, Solomon, Gödel's functional (“Dialectica”) interpretation, Handbook ofproof theory, Studies in Logic and the Foundations of Mathematics, vol. 137, North-Holland, Amsterdam, 1998, pp. 337–405.Google Scholar
[4] Barwise, Jon and Schlipf, John, On recursively saturated models of arithmetic, Model theory and algebra (A memorial tribute to Abraham Robinson), Lecture Notes in Mathematics, vol. 498, Springer, Berlin, 1975, pp. 42–55.Google Scholar
[5] Bezem, Marc, Strongly majorizable functionals offinite type: a model for bar recursion containing discontinuous functionals, this Journal, vol. 50 (1985), no. 3, pp. 652–660.Google Scholar
[6] Bovykin, Andrey and Weiermann, Andreas, The strength of infinitary Ramseyan principles can be accessed by their densities, accepted for publication in Annals of Pure and Applied Logic , http://logic.pdmi.ras.ru/~andrey/research.html, 2005.Google Scholar
[7] Cholak, Peter A., Jockusch, Carl G. Jr., and Slaman, Theodore A., On the strength of Ramsey's theorem for pairs, this Journal, vol. 66 (2001), no. 1, pp. 1–55.Google Scholar
[8] Cholak, Peter A., Jockusch, Carl G. Jr., and Slaman, Theodore A., Corrigendum to: “On the strength of Ramsey's theorem for pairs”, this Journal, vol. 74 (2009), no. 4, pp. 1438–1439.Google Scholar
[9] Chong, Chitat, Slaman, Theodore, and Yang, Yue, -conservation of combinatorial principles weaker than Ramsey's theorem for pairs, preprint, available at http://www.math.nus.edu.sg/~chongct/C0H-10.pdf.Google Scholar
[10] Chong, Chitat T., Nonstandard methods in Ramsey's theorem for pairs, Computational prospects of infinity. Part II. Presented talks, Lecture Notes Series. Institute for Mathematical Sciences. National University of Singapore, vol. 15, World Scientific Publishing, Hackensack, NJ, 2008, pp. 47–57.Google Scholar
[11] Friedman, Harvey, Some systems of second order arithmetic and their use, Proceedings of the International Congress of Mathematicians ( Vancouver, B.C., 1974), vol. 1, Canadian Mathematics Congress, Montreal, Quebec, 1975, pp. 235–242.Google Scholar
[12] Gandy, Robin O., Proofs of strong normalization, To H. B. Curry: essays on combinatory logic, lambda calculus and formalism. Academic Press, London, 1980, pp. 457–477.Google Scholar
[13] Gödel, Kurt, Über eine bisher noch nicht benützte Erweiterung des finiten Standpunktes, Dialectica, vol. 12 (1958), pp. 280–287.Google Scholar
[14] Hájek, Petr and Pudlák, Pavel, Metamathematics of first-order arithmetic, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1998.Google Scholar
[15] Hirschfeldt, Denis R. and Shore, Richard A., Combinatorial principles weaker than Ramsey's theorem for pairs, this Journal, vol. 72 (2007), no. 1, pp. 171–206.Google Scholar
[16] Hirst, Jeffry L., Combinatorics in subsystems of second order arithmetic, Ph.D. thesis, Pennsylvania State University, 1987.Google Scholar
[17] Howard, William A., Ordinal analysis of terms of finite type, this Journal, vol. 45 (1980), no. 3, pp. 493–504.Google Scholar
[18] Howard, William A., Ordinal analysis of simple cases of bar recursion, this Journal, vol. 46 (1981), no. 1, pp. 17–30.Google Scholar
[19] Jockusch, Carl and Stephan, Frank, A cohesive set which is not high, Mathematical Logic Quarterly, vol. 39 (1993), no. 4, pp. 515–530.Google Scholar
[20] Jockusch, Carl and Stephan, Frank, Correction to: “A cohesive set which is not high”, Mathematical Logic Quarterly, vol. 43 (1997), no. 4, p. 569.Google Scholar
[21] Jockusch, Carl G. Jr., Ramsey's theorem and recursion theory, this Journal, vol. 37 (1972), pp. 268–280.Google Scholar
[22] Jockusch, Carl G. Jr. and Soare, Robert I., classes and degrees of theories, Transactions of the American Mathematical Society, vol. 173 (1972), pp. 33–56.Google Scholar
[23] Kleene, Stephen C., Countable functionals, Constructivity in mathematics: Proceedings of the colloquium held at Amsterdam, 1957 (Heyting, A., editor), Studies in Logic and the Foundations of Mathematics, North-Holland, Amsterdam, 1959, pp. 81–100.Google Scholar
[24] Kleene, Stephen C, Recursive functionals and quantifiers of finite types. I, Transactions of the American Mathematical Society, vol. 91 (1959), pp. 1–52.Google Scholar
[25] Kohlenbach, Ulrich, Effective bounds from ineffective proofs in analysis: an application of functional interpretation andmajorization, this Journal, vol. 57 (1992), no. 4, pp. 1239–1273.Google Scholar
[26] Kohlenbach, Ulrich, Mathematically strong subsystems of analysis with low rate of growth ofprovably recursive functionals, Archive for Mathematical Logic, vol. 36 (1996), no. 1, pp. 31–71.Google Scholar
[27] Kohlenbach, Ulrich, Elimination of Skolem functions for monotone formulas in analysis. Archive for Mathematical Logic, vol. 37 (1998), pp. 363–390.Google Scholar
[28] Kohlenbach, Ulrich, On the arithmetical content of restricted forms of comprehension, choice and general uniform boundedness, Annals of Pure and Applied Logic, vol. 95 (1998), pp. 257–285.Google Scholar
[29] Kohlenbach, Ulrich, On the no-counterexample interpretation, this Journal, vol. 64 (1999), no. 4, pp. 1491–1511.Google Scholar
[30] Kohlenbach, Ulrich, On uniform weak Königs lemma, Annals of Pure and Applied Logic, vol. 114 (2002), no. 1–3, pp. 103–116, Commemorative symposium dedicated to Anne S. Troelstra (Noordwijkerhout, 1999).Google Scholar
[31] Kohlenbach, Ulrich, Higher order reverse mathematics, Reverse mathematics 2001, Lecture Notes in Logic, vol. 21, Association for Symbolic Logic, La Jolla, CA, 2005, pp. 281–295.Google Scholar
[32] Kohlenbach, Ulrich, Applied proof theory: Proof interpretations and their use in mathematics, Springer Monographs in Mathematics, Springer Verlag, 2008.Google Scholar
[33] Kreisel, Georg, Interpretation of analysis by means of constructive functionals of finite types, Constructivity in mathematics: Proceedings of the colloquium held at Amsterdam, 1957 (Heyting, A., editor), Studies in Logic and the Foundations of Mathematics, North-Holland, Amsterdam, 1959, pp. 101–128.Google Scholar
[34] Kreuzer, Alexander and Kohlenbach, Ulrich, Ramsey's theorem for pairs and provably recursive functions, Notre Dame Journal of Formal Logic, vol. 50 (2009), no. 4, pp. 427–444 (2010).Google Scholar
[35] Kreuzer, Alexander P., Der Satz von Ramsey für Paare und beweisbar rekursive Funktionen, Diploma Thesis, Technische Universität Darmstadt, 2009.Google Scholar
[36] Kreuzer, Alexander P., The cohesive principle and the Bolzano-Weierstraß principle, Mathematical Logic Quarterly, vol. 57 (2011), no. 3, pp. 292–298.Google Scholar
[37] Kreuzer, Alexander P., Primitive recursion and the chain antichain principle, Notre Dame Journal of Formal Logic, vol. 53 (2012), no. 2, pp. 245–265.Google Scholar
[38] Luckhardt, Horst, Extensional Gödel functional interpretation. A consistency proof of classical analysis, Lecture Notes in Mathematics, vol. 306, Springer-Verlag, Berlin, 1973.Google Scholar
[39] Normann, Dag, Recursion on the countable functionals, Lecture Notes in Mathematics, vol. 811, Springer, Berlin, 1980.Google Scholar
[40] Parsons, Charles, Proof-theoretic analysis of restricted induction schemata, Meetings of the Association for Symbolic Logic (Takeuti, Gaisi, editor), Association for Symbolic Logic, 1971, abstract, p. 361.Google Scholar
[41] Parsons, Charles, On n-quantifier induction, this Journal, vol. 37 (1972), pp. 466–482.Google Scholar
[42] Safarik, Pavol and Kohlenbach, Ulrich, On the computational content of the Bolzano-Weierstraß principle, Mathematical Logic Quarterly, vol. 56 (2010), no. 5, pp. 508–532.Google Scholar
[43] Seetapun, David and Slaman, Theodore A., On the strength of Ramsey's theorem, Notre Dame Journal of Formal Logic, vol. 36 (1995), no. 4, pp. 570–582, Special Issue: Models of arithmetic.Google Scholar
[44] Shore, Richard A., Reverse mathematics: the playground of logic. The Bulletin of Symbolic Logic, vol. 16 (2010), no. 3, pp. 378–402.Google Scholar
[45] Simpson, Stephen G., Subsystems of second order arithmetic, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1999.Google Scholar
[46] Soare, Robert I., Recursively enumerable sets and degrees, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1987.Google Scholar
[47] Specker, Ernst, Ramsey's theorem does not hold in recursive set theory, Logic Colloquium '69 (Proceedings of the Summer School and Colloquium, Manchester, 1969), North-Holland, Amsterdam, 1971, pp. 439–442.CrossRefGoogle Scholar
[48] Spector, Clifford, Provably recursive functionals of analysis: a consistency proof of analysis by an extension ofprinciples formulated in current intuitionistic mathematics, Proceedings of the Symposium in Pure Mathematics, vol. V, American Mathematical Society, Providence, R.I., 1962, pp. 1–27.Google Scholar
[49] Streicher, Thomas and Kohlenbach, Ulrich, Shoenfield is Gödel after Krivine, Mathematical Logic Quarterly, vol. 53 (2007), no. 2, pp. 176–179.Google Scholar
[50] Takeuti, Gaisi, Two applications of logic to mathematics, Iwanami Shoten, Tokyo, 1978, Kanô Memorial Lectures, vol. 3, Publications of the Mathematical Society of Japan, no. 13.Google Scholar
[51] Troelstra, Anne S. (editor), Metamathematical investigation of intuitionistic arithmetic and analysis, Lecture Notes in Mathematics, vol. 344, Springer-Verlag, Berlin, 1973.Google Scholar
[52] Troelstra, Anne S., Note on the fan theorem, this Journal, vol. 39 (1974), pp. 584–596.Google Scholar
[53] Weiermann, Andreas, How is it that infinitary methods can be applied to finitary mathematics? Gödel's T: a case study, this Journal, vol. 63 (1998), no. 4, pp. 1348–1370.Google Scholar