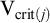1 Introduction
A vital tool in many set-theoretic arguments is the assumption that various large cardinal notions are consistent. That is, it is possible to have a cardinal which exhibits certain additional properties that cannot provably exist arguing from ZFC alone. Often these properties can be expressed using the first ordinal moved, or the critical point, of an elementary embedding
where M is some transitive class, with the general principle being that the closer M is to V, the stronger the resulting large cardinal assumption. For example, the critical point is said to be
![]() $\lambda $
-strong if
$\lambda $
-strong if
or
![]() $\lambda $
-supercompact if M is closed under arbitrary sequences of length
$\lambda $
-supercompact if M is closed under arbitrary sequences of length
![]() $\lambda $
.
$\lambda $
.
There is a natural limit to these large cardinals, originally proposed by Reinhardt [Reference Solovay, Reinhardt and Kanamori21], which is for
![]() $\kappa $
to be the critical point of a non-trivial elementary embedding from V to itself. However, as shown by Kunen [Reference Kunen17] there is no such non-trivial embedding when V is a model of ZFC along with a predicate for j such that V satisfies all instances of Replacement and Separation in the language expanded to include this predicate. In fact, Kunen’s proof shows that there is no non-trivial elementary embedding
$\kappa $
to be the critical point of a non-trivial elementary embedding from V to itself. However, as shown by Kunen [Reference Kunen17] there is no such non-trivial embedding when V is a model of ZFC along with a predicate for j such that V satisfies all instances of Replacement and Separation in the language expanded to include this predicate. In fact, Kunen’s proof shows that there is no non-trivial elementary embedding
for any ordinal
![]() $\lambda $
under the assumption that V satisfies ZFC.
$\lambda $
under the assumption that V satisfies ZFC.
Since the announcement of this result it has been a long standing and much studied question as to whether or not the Axiom of Choice is necessary for this result. Namely, if it is consistent for there to be a non-trivial elementary embedding
![]() under the assumption that V is a model of ZF. In this paper we take a different approach to generalising Kunen’s inconsistency which is to study such embeddings in the theory ZFC without Power Set. The motivation for this is the following result which shows that such embeddings are consistent under the assumption that
under the assumption that V is a model of ZF. In this paper we take a different approach to generalising Kunen’s inconsistency which is to study such embeddings in the theory ZFC without Power Set. The motivation for this is the following result which shows that such embeddings are consistent under the assumption that
![]() is consistent, which is an axiom just short of the Kunen inconsistency. In particular,
is consistent, which is an axiom just short of the Kunen inconsistency. In particular,
![]() will give a non-trivial embedding from
will give a non-trivial embedding from
![]() to itself, which is one of the standard structures which models ZFC without Power Set.
to itself, which is one of the standard structures which models ZFC without Power Set.
Theorem 2.2. There exists a non-trivial elementary embedding
![]() if and only if there exists a non-trivial elementary embedding
if and only if there exists a non-trivial elementary embedding
![]() .
.
It is a well-known result that without Power Set many of the usual equivalent ways to formulate the axioms of ZFC break down. In particular, the Replacement Scheme no longer implies the stronger Collection Scheme and the Axiom of Choice does not imply that every set can be well-ordered. Without the Collection Scheme many of the basic facts that one assumes no longer hold, for example we can consistently have that
![]() $\omega _1$
exists and is singular or that the Łoś ultrapower theorem can fail. One can find these and other similar results in [Reference Gitman, Hamkins and Johnstone7]. So, using the notation found in that paper, we shall define the theory ZFC without Power Set as follows:
$\omega _1$
exists and is singular or that the Łoś ultrapower theorem can fail. One can find these and other similar results in [Reference Gitman, Hamkins and Johnstone7]. So, using the notation found in that paper, we shall define the theory ZFC without Power Set as follows:
Definition 1.1. Let
![]() denote the theory consisting of the following axioms: Empty set, Extensionality, Pairing, Unions, Infinity, the Foundation Scheme, the Separation Scheme and the Replacement Scheme.
denote the theory consisting of the following axioms: Empty set, Extensionality, Pairing, Unions, Infinity, the Foundation Scheme, the Separation Scheme and the Replacement Scheme.
-
 denotes the theory
denotes the theory
 plus the Collection Scheme.
plus the Collection Scheme. -
 denotes the theory
denotes the theory
 plus the Well-Ordering Principle.
plus the Well-Ordering Principle. -
 denotes the theory
denotes the theory
 plus the Reflection Principle.
plus the Reflection Principle.
We will also use the corresponding notation for their second order versions
![]() and
and
![]() .
.
The main result of this paper is that, under mild assumptions, Kunen’s inconsistency does still hold in the theory
![]() (the theory
(the theory
![]() with a predicate for j) and therefore that, while
with a predicate for j) and therefore that, while
![]() has more structure than
has more structure than
![]() , the embedding given by
, the embedding given by
![]() cannot have one of the most useful properties an embedding can have, cofinality.
cannot have one of the most useful properties an embedding can have, cofinality.
Theorem 5.4. There is no non-trivial, cofinal,
![]() $\Sigma _0$
-elementary embedding
$\Sigma _0$
-elementary embedding
![]() such that
such that
![]() and
and
![]() .
.
The proof of the above theorem makes essential use of the fact that the initial segment of the universe up to the critical point of j,
![]() is a set. However, by strengthening the underlying theory to also satisfy
is a set. However, by strengthening the underlying theory to also satisfy
![]() , which is the
, which is the
![]() -Scheme for every cardinal
-Scheme for every cardinal
![]() $\mu $
, this can be removed.
$\mu $
, this can be removed.
Corollary 6.10. There is no non-trivial, cofinal,
![]() $\Sigma _0$
-elementary embedding
$\Sigma _0$
-elementary embedding
![]() such that
such that
![]() .
.
The second half of the paper deals with a curious property of the theory
![]() which is needed for the above result. This is the property that if V is a model of
which is needed for the above result. This is the property that if V is a model of
![]() and
and
![]() $\mathcal {C}$
is a definable proper class over V then for any non-zero ordinal
$\mathcal {C}$
is a definable proper class over V then for any non-zero ordinal
![]() $\gamma $
there is a definable surjection of
$\gamma $
there is a definable surjection of
![]() $\mathcal {C}$
onto
$\mathcal {C}$
onto
![]() $\gamma $
. A reasonable suggestion for a counter-example to this property without Choice is to construct a model of
$\gamma $
. A reasonable suggestion for a counter-example to this property without Choice is to construct a model of
![]() with an amorphous class, where
with an amorphous class, where
Definition 7.3. A class A is said to be amorphous if it is infinite but not the disjoint union of two infinite subclasses. Namely, if
![]() $A = B \cup C$
and
$A = B \cup C$
and
![]() $B \cap C = \emptyset $
then either B or C must be a finite set.
$B \cap C = \emptyset $
then either B or C must be a finite set.
Note that such a class could not surject onto
![]() $\omega $
otherwise it could be partitioned into the class mapped to even numbers and the class mapped to odd numbers.
$\omega $
otherwise it could be partitioned into the class mapped to even numbers and the class mapped to odd numbers.
However, we show that, without Choice, many structures which would otherwise satisfy Collection only satisfy the Replacement Scheme. This is done by proving the following result which shows that the existence of an amorphous proper class implies the failure of Collection and thus a failure of our hoped-for counter-example. Moreover, using this we can show that a symmetric submodel of a pretame class forcing need not model the Collection Scheme.
Theorem 7.13. Suppose that
![]() satisfies;
satisfies;
-
1.
 ,
, -
2.
 and
and
 and
and -
3.

Then the Collection Scheme fails in
![]() . Moreover,
. Moreover,
![]() does not have a cumulative hierarchy and therefore Power Set also fails.
does not have a cumulative hierarchy and therefore Power Set also fails.
2 Embeddings of

Definition 2.1.
![]() is the assertion that for some ordinal
is the assertion that for some ordinal
![]() $\lambda $
there exists a non-trivial elementary embedding
$\lambda $
there exists a non-trivial elementary embedding
![]() .
.
![]() is considered one of the strongest large cardinal axioms that is not known to be inconsistent. The following result is adapted from the folklore result which gives an alternate characterisation of 1-extendible cardinals, a proof of which can be found in [Reference Brooke-Taylor1]. This theorem shows an equivalent way of considering
is considered one of the strongest large cardinal axioms that is not known to be inconsistent. The following result is adapted from the folklore result which gives an alternate characterisation of 1-extendible cardinals, a proof of which can be found in [Reference Brooke-Taylor1]. This theorem shows an equivalent way of considering
![]() embeddings as embeddings of
embeddings as embeddings of
![]() , a set with much more structure than
, a set with much more structure than
![]() .
.
For convenience, we note here that the Kunen inconsistency can be proved in
![]() , so there is no non-trivial elementary embedding from
, so there is no non-trivial elementary embedding from
![]() to itself. This can be seen by carefully analysing the second proof of Theorem 23.12 in [Reference Kanamori13] or equivalently by using Theorem 5.2.
to itself. This can be seen by carefully analysing the second proof of Theorem 23.12 in [Reference Kanamori13] or equivalently by using Theorem 5.2.
Theorem 2.2. There exists a non-trivial elementary embedding
![]() if and only if there exists a non-trivial elementary embedding
if and only if there exists a non-trivial elementary embedding
![]() .
.
Proof.
![]() $(\Leftarrow ):$
By the Kunen inconsistency,
$(\Leftarrow ):$
By the Kunen inconsistency,
![]() $\lambda $
must be the supremum of the critical sequence
$\lambda $
must be the supremum of the critical sequence
![]() $\langle \kappa _n \colon n \in \omega \rangle $
of j, where
$\langle \kappa _n \colon n \in \omega \rangle $
of j, where
![]() $\kappa _0$
is the critical point and
$\kappa _0$
is the critical point and
![]() $\kappa _{n + 1} = j(\kappa _n)$
. Then each
$\kappa _{n + 1} = j(\kappa _n)$
. Then each
![]() $\kappa _n$
is an inaccessible cardinal and thus
$\kappa _n$
is an inaccessible cardinal and thus
![]() $2^{< \lambda } = \lambda = \beth _\lambda $
. Therefore
$2^{< \lambda } = \lambda = \beth _\lambda $
. Therefore
![]() and
and
![]() so
so
![]() . This means that
. This means that
![]() , so
, so
![]() is a definable class in
is a definable class in
![]() . Moreover, working in
. Moreover, working in
![]() , any formula
, any formula
![]() $\varphi $
can be relativised to
$\varphi $
can be relativised to
![]() so
so
![]() is elementary.
is elementary.
![]() $(\Rightarrow ):$
We begin by defining a standard way to code elements of
$(\Rightarrow ):$
We begin by defining a standard way to code elements of
![]() by elements of
by elements of
![]() . This will be done by coding
. This will be done by coding
![]() ${\textrm {trcl}}(\{x\})$
by some subset of
${\textrm {trcl}}(\{x\})$
by some subset of
![]() $\lambda \times \lambda $
whose Mostowski collapse is again
$\lambda \times \lambda $
whose Mostowski collapse is again
![]() ${\textrm {trcl}}(\{x\})$
. However, since we will be working with
${\textrm {trcl}}(\{x\})$
. However, since we will be working with
![]() ${\textrm {trcl}}(\{x\})$
rather than x itself, it is necessary to do a simple, preliminary coding.
${\textrm {trcl}}(\{x\})$
rather than x itself, it is necessary to do a simple, preliminary coding.
So, let
![]() . For
. For
![]() define the relation
define the relation
![]() $\operatorname {\mathrm {\hat {\in }}}$
by
$\operatorname {\mathrm {\hat {\in }}}$
by
![]() ${\textrm {trcl}}(\{x\}) \mathbin{\operatorname {\mathrm {\hat {\in }}}} {\textrm {trcl}}(\{y\})$
if and only if
${\textrm {trcl}}(\{x\}) \mathbin{\operatorname {\mathrm {\hat {\in }}}} {\textrm {trcl}}(\{y\})$
if and only if
![]() $x \in y$
and similarly for
$x \in y$
and similarly for
![]() $\operatorname {\mathrm {\hat {=}}}$
. It is then clear that any first order statement
$\operatorname {\mathrm {\hat {=}}}$
. It is then clear that any first order statement
![]() $\varphi $
about
$\varphi $
about
![]() is equivalent to a formula
is equivalent to a formula
![]() $\hat {\varphi }$
over
$\hat {\varphi }$
over
![]() by the obvious coding.
by the obvious coding.
Now note that
![]() ${\textrm {rank}}(\lambda \times \lambda ) = \lambda $
and so any subset of
${\textrm {rank}}(\lambda \times \lambda ) = \lambda $
and so any subset of
![]() $\lambda \times \lambda $
has rank at most
$\lambda \times \lambda $
has rank at most
![]() $\lambda $
. So, for any
$\lambda $
. So, for any
and bijection
![]() $f \colon |{\textrm {trcl}}(\{x\})| \rightarrow {\textrm {trcl}}(\{x\})$
let
$f \colon |{\textrm {trcl}}(\{x\})| \rightarrow {\textrm {trcl}}(\{x\})$
let
Then the Mostowski collapse of
![]() $C_{x,f}$
,
$C_{x,f}$
,
![]() ${\textrm {coll}}(C_{x,f})$
, is
${\textrm {coll}}(C_{x,f})$
, is
![]() ${\textrm {trcl}}(\{x\})$
. Let
${\textrm {trcl}}(\{x\})$
. Let
![]() $\tilde {H}$
denote the definable class in
$\tilde {H}$
denote the definable class in
of all subsets of
![]() $\lambda \times \lambda $
which code an element of
$\lambda \times \lambda $
which code an element of
in this way. That is
![]() $X \in \tilde {H}$
iff X is a well-founded, extensional, binary relation on
$X \in \tilde {H}$
iff X is a well-founded, extensional, binary relation on
![]() $\lambda $
with a single maximal element and
$\lambda $
with a single maximal element and
![]() ${\textrm {dom}}(X) \cup {\textrm {ran}}(X)$
is a cardinal which is at most
${\textrm {dom}}(X) \cup {\textrm {ran}}(X)$
is a cardinal which is at most
![]() $\lambda $
.
$\lambda $
.
For
![]() $Z \in \tilde {H}$
, let
$Z \in \tilde {H}$
, let
![]() ${\textrm {fld}}(Z)$
be
${\textrm {fld}}(Z)$
be
![]() ${\textrm {dom}}(Z) \cup {\textrm {ran}}(Z)$
and define
${\textrm {dom}}(Z) \cup {\textrm {ran}}(Z)$
and define
![]() ${\textrm {max}}(Z)$
to be the unique element of
${\textrm {max}}(Z)$
to be the unique element of
![]() ${\textrm {fld}}(Z)$
which is maximal with respect to the relation on Z. Now, for
${\textrm {fld}}(Z)$
which is maximal with respect to the relation on Z. Now, for
![]() $X, Y \in \tilde {H}$
define relations
$X, Y \in \tilde {H}$
define relations
![]() $\operatorname {\mathrm {\tilde {=}}}$
and
$\operatorname {\mathrm {\tilde {=}}}$
and
![]() $\operatorname {\mathrm {\tilde {\in }}}$
by:
$\operatorname {\mathrm {\tilde {\in }}}$
by:
 $$ \begin{align*} X \mathbin{\operatorname{\mathrm{\tilde{=}}}} Y \Longleftrightarrow \exists g \colon \lambda \rightarrow \lambda \ &\bigg( g \textit{ is a bijection} \wedge \forall \alpha, \beta \in \lambda \\ &\qquad\qquad\qquad\qquad\big( \langle \alpha, \beta \rangle \in X \leftrightarrow \langle g(\alpha), g(\beta) \rangle \in Y \big) \bigg), \end{align*} $$
$$ \begin{align*} X \mathbin{\operatorname{\mathrm{\tilde{=}}}} Y \Longleftrightarrow \exists g \colon \lambda \rightarrow \lambda \ &\bigg( g \textit{ is a bijection} \wedge \forall \alpha, \beta \in \lambda \\ &\qquad\qquad\qquad\qquad\big( \langle \alpha, \beta \rangle \in X \leftrightarrow \langle g(\alpha), g(\beta) \rangle \in Y \big) \bigg), \end{align*} $$
 $$ \begin{align*} X \mathbin{\operatorname{\mathrm{\tilde{\in}}}} Y \Longleftrightarrow \exists g \colon \lambda & \rightarrow \lambda \ \bigg( g \textit{ is injective} \wedge \langle g({\textrm{max}}(X)), {\textrm{max}}(Y) \rangle \in Y \\ & \wedge \forall \alpha, \beta \in {\textrm{fld}}(X) \ \big( \langle \alpha, \beta \rangle \in X \leftrightarrow \langle g(\alpha), g(\beta) \rangle \in Y \big) \\ & \wedge \forall \gamma \in {\textrm{fld}}(Y) \ \forall \delta \in {\textrm{fld}}(X) \\ & \phantom{\wedge \forall \gamma \in {\textrm{fld}}} \big( \langle \gamma, g(\delta) \rangle \in Y \rightarrow \exists \sigma \in {\textrm{fld}}(X) \ \sigma = g(\gamma) \big) \bigg).^{1} \end{align*} $$
$$ \begin{align*} X \mathbin{\operatorname{\mathrm{\tilde{\in}}}} Y \Longleftrightarrow \exists g \colon \lambda & \rightarrow \lambda \ \bigg( g \textit{ is injective} \wedge \langle g({\textrm{max}}(X)), {\textrm{max}}(Y) \rangle \in Y \\ & \wedge \forall \alpha, \beta \in {\textrm{fld}}(X) \ \big( \langle \alpha, \beta \rangle \in X \leftrightarrow \langle g(\alpha), g(\beta) \rangle \in Y \big) \\ & \wedge \forall \gamma \in {\textrm{fld}}(Y) \ \forall \delta \in {\textrm{fld}}(X) \\ & \phantom{\wedge \forall \gamma \in {\textrm{fld}}} \big( \langle \gamma, g(\delta) \rangle \in Y \rightarrow \exists \sigma \in {\textrm{fld}}(X) \ \sigma = g(\gamma) \big) \bigg).^{1} \end{align*} $$
Then
![]() $\operatorname {\mathrm {\tilde {=}}}$
and
$\operatorname {\mathrm {\tilde {=}}}$
and
![]() $\operatorname {\mathrm {\tilde {\in }}}$
are definable in
$\operatorname {\mathrm {\tilde {\in }}}$
are definable in
![]() ,
,
![]() $X \mathbin{\operatorname {\mathrm {\tilde {=}}}} Y \Leftrightarrow {\textrm {coll}}(X) = {\textrm {coll}}(Y)$
and
$X \mathbin{\operatorname {\mathrm {\tilde {=}}}} Y \Leftrightarrow {\textrm {coll}}(X) = {\textrm {coll}}(Y)$
and
![]() $X \mathbin{\operatorname {\mathrm {\tilde {\in }}}} Y \Leftrightarrow {\textrm {coll}}(X) \in {\textrm {coll}}(Y)$
. Now we have that any first order statement
$X \mathbin{\operatorname {\mathrm {\tilde {\in }}}} Y \Leftrightarrow {\textrm {coll}}(X) \in {\textrm {coll}}(Y)$
. Now we have that any first order statement
![]() $\hat {\varphi }$
about
$\hat {\varphi }$
about
![]() is equivalent to a formula
is equivalent to a formula
![]() $\tilde {\varphi }$
over
$\tilde {\varphi }$
over
![]() which is defined by the following coding:
which is defined by the following coding:
-
• Replace any parameter
 ${\textrm {trcl}}(\{x\})$
occurring in
${\textrm {trcl}}(\{x\})$
occurring in
 $\hat {\varphi }$
with
$\hat {\varphi }$
with
 $C_{x, f}$
for some (any) bijection
$C_{x, f}$
for some (any) bijection
 $f \colon |{\textrm {trcl}}(\{x\})| \rightarrow {\textrm {trcl}}(\{x\})$
.
$f \colon |{\textrm {trcl}}(\{x\})| \rightarrow {\textrm {trcl}}(\{x\})$
. -
• Replace any instance of
 $\operatorname {\mathrm {\hat {=}}}$
with
$\operatorname {\mathrm {\hat {=}}}$
with
 $\operatorname {\mathrm {\tilde {=}}}$
and
$\operatorname {\mathrm {\tilde {=}}}$
and
 $\operatorname {\mathrm {\hat {\in }}}$
with
$\operatorname {\mathrm {\hat {\in }}}$
with
 $\operatorname {\mathrm {\tilde {\in }}}$
.
$\operatorname {\mathrm {\tilde {\in }}}$
. -
• Replace any unbounded quantification by the same quantifier taken over
 $\tilde {H}$
.
$\tilde {H}$
.
Then, by the elementarity of k,
 $$ \begin{align*} X \mathbin{\operatorname{\mathrm{\tilde{=}}}} Y & \Longleftrightarrow k(X) \mathbin{\operatorname{\mathrm{\tilde{=}}}} k(Y) \\ & \textrm{ and } \\ X \mathbin{\operatorname{\mathrm{\tilde{\in}}}} Y & \Longleftrightarrow k(X) \mathbin{\operatorname{\mathrm{\tilde{\in}}}} k(Y). \end{align*} $$
$$ \begin{align*} X \mathbin{\operatorname{\mathrm{\tilde{=}}}} Y & \Longleftrightarrow k(X) \mathbin{\operatorname{\mathrm{\tilde{=}}}} k(Y) \\ & \textrm{ and } \\ X \mathbin{\operatorname{\mathrm{\tilde{\in}}}} Y & \Longleftrightarrow k(X) \mathbin{\operatorname{\mathrm{\tilde{\in}}}} k(Y). \end{align*} $$
Also, since
![]() is a definable class in
is a definable class in
![]() the restriction of the embedding
the restriction of the embedding
![]() is still elementary.
is still elementary.
So we can define
by setting
![]() $j(x)$
to be the unique element of
$j(x)$
to be the unique element of
![]() ${\textrm {coll}}(k(C_{x,f}))$
of maximal rank for some bijection
${\textrm {coll}}(k(C_{x,f}))$
of maximal rank for some bijection
![]() $f \colon | {\textrm {trcl}}(\{x\})| \rightarrow {\textrm {trcl}}(\{x\})$
. Moreover j is elementary since
$f \colon | {\textrm {trcl}}(\{x\})| \rightarrow {\textrm {trcl}}(\{x\})$
. Moreover j is elementary since

⊣
The above theorem shows that the existence of a non-trivial elementary embedding from V to itself under
![]() is weaker than
is weaker than
![]() , however it does not show that the embedding one obtains has any useful structure. What we shall show is that this embedding must fail one of the most useful fundamental characteristics, that of cofinality where
, however it does not show that the embedding one obtains has any useful structure. What we shall show is that this embedding must fail one of the most useful fundamental characteristics, that of cofinality where
Definition 2.3. An embedding
![]() is said to be cofinal if for every
is said to be cofinal if for every
![]() there is an
there is an
![]() such that
such that
![]() $y \in j(x)$
.
$y \in j(x)$
.
Remark 2.4. If M satisfies ZF and
![]() then the cumulative hierarchy for M witnesses that any elementary embedding is cofinal.
then the cumulative hierarchy for M witnesses that any elementary embedding is cofinal.
3 Definable embeddings
We begin this section with a standard fact about non-trivial elementary embeddings which is that they must move an ordinal. The only notable thing about the statement is that the proof only requires elementarity for bounded formulae.
Proposition 3.1. Suppose that
![]() are transitive class models of
are transitive class models of
![]() and
and
![]() is a non-trivial,
is a non-trivial,
![]() $\Sigma _0$
-elementary embedding. Then there exists an ordinal
$\Sigma _0$
-elementary embedding. Then there exists an ordinal
![]() $\alpha $
such that
$\alpha $
such that
![]() $j(\alpha )> \alpha $
.
$j(\alpha )> \alpha $
.
Proof. First note that
![]() $\Sigma _0$
-elementarity implies
$\Sigma _0$
-elementarity implies
![]() $\Delta _1$
-elementarity. Now, since being an ordinal is
$\Delta _1$
-elementarity. Now, since being an ordinal is
![]() $\Sigma _0$
definable, if
$\Sigma _0$
definable, if
![]() $\alpha $
is an ordinal then so is
$\alpha $
is an ordinal then so is
![]() $j(\alpha )$
. Next, since
$j(\alpha )$
. Next, since
![]() $\emptyset $
is definable as the unique set z such that
$\emptyset $
is definable as the unique set z such that
![]() $\forall y \in z \ (y \neq y)$
, which is a
$\forall y \in z \ (y \neq y)$
, which is a
![]() $\Sigma _0$
formula,
$\Sigma _0$
formula,
![]() $j(\emptyset ) = \emptyset $
. So, by induction, we have that for every ordinal
$j(\emptyset ) = \emptyset $
. So, by induction, we have that for every ordinal
![]() $\alpha $
,
$\alpha $
,
![]() $j(\alpha ) \geq \alpha $
. Now let x be a set of least rank such that
$j(\alpha ) \geq \alpha $
. Now let x be a set of least rank such that
![]() $j(x) \neq x$
and let
$j(x) \neq x$
and let
![]() $\delta = {\textrm {rank}}(x)$
. Then for all
$\delta = {\textrm {rank}}(x)$
. Then for all
![]() $y \in x$
,
$y \in x$
,
![]() $y = j(y) \in j(x)$
so
$y = j(y) \in j(x)$
so
![]() $x \subseteq j(x)$
. Thus there must be some
$x \subseteq j(x)$
. Thus there must be some
![]() $z \in j(x) \setminus x$
. Now suppose that
$z \in j(x) \setminus x$
. Now suppose that
![]() ${\textrm {rank}}(j(x)) = \delta $
, then we must have that
${\textrm {rank}}(j(x)) = \delta $
, then we must have that
![]() $j(z) = z \in j(x)$
so, by elementarity,
$j(z) = z \in j(x)$
so, by elementarity,
![]() $z \in x$
which yields a contradiction. Hence, since the following is
$z \in x$
which yields a contradiction. Hence, since the following is
![]() $\Delta _1$
definable, we must have that
$\Delta _1$
definable, we must have that
![]() $j(\delta ) = {\textrm {rank}}(j(x))> \delta $
.⊣
$j(\delta ) = {\textrm {rank}}(j(x))> \delta $
.⊣
Therefore, given a non-trivial,
![]() $\Sigma _0$
-elementary
$\Sigma _0$
-elementary
![]() , we will define the critical point of j to be the least ordinal moved and denote it by
, we will define the critical point of j to be the least ordinal moved and denote it by
![]() ${\textrm {crit}}(\textit {j})$
.
${\textrm {crit}}(\textit {j})$
.
It is not a priori obvious that being an elementary embedding should be definable by a single sentence. However, as proven by Gaifman in [Reference Gaifman5], if M is a model of a sufficient fragmentFootnote
2
of ZFC then it suffices to check that a cofinal embedding is elementary for
![]() $\Sigma _0$
sentences. The version below for the case where
$\Sigma _0$
sentences. The version below for the case where
![]() appears in [Reference Gitman, Hamkins and Johnstone7].
appears in [Reference Gitman, Hamkins and Johnstone7].
Theorem 3.2 (Gaifman).
Suppose that M is a model of
![]() and
and
![]() is a cofinal,
is a cofinal,
![]() $\Sigma _0$
-elementary embedding. Then j is fully elementary.
$\Sigma _0$
-elementary embedding. Then j is fully elementary.
Remark 3.3. This theorem does not require any assumptions on N. Moreover, the models M and N need not be transitive.
Using the fact that being
![]() $\Sigma _0$
-elementary is definable by a single formula we obtain a version of Suzuki’s theorem on the non-definability of embeddings [Reference Suzuki22], in the context of
$\Sigma _0$
-elementary is definable by a single formula we obtain a version of Suzuki’s theorem on the non-definability of embeddings [Reference Suzuki22], in the context of
![]() .
.
Theorem 3.4 (Suzuki).
Assume that
![]() . Then there is no non-trivial, cofinal, elementary embedding
. Then there is no non-trivial, cofinal, elementary embedding
![]() which is definable from parameters.
which is definable from parameters.
Proof. Formally, this is a theorem scheme asserting that for each formula
![]() $\varphi $
there is no parameter p for which
$\varphi $
there is no parameter p for which
![]() $\varphi (\cdot , \cdot , p)$
defines a non-trivial, cofinal, elementary embedding
$\varphi (\cdot , \cdot , p)$
defines a non-trivial, cofinal, elementary embedding
. Using Theorem 3.2, it suffices to show that for no parameter p are we able to define a non-trivial, cofinal,
![]() $\Sigma _0$
-elementary embedding
$\Sigma _0$
-elementary embedding
by
So, seeking a contradiction, let
![]() $\sigma (p)$
be the sentence asserting that
$\sigma (p)$
be the sentence asserting that
![]() $\varphi (\cdot , \cdot , p)$
defines a
$\varphi (\cdot , \cdot , p)$
defines a
![]() $\Sigma _0$
-elementary embedding and let
$\Sigma _0$
-elementary embedding and let
![]() $\psi (p)$
asserts that
$\psi (p)$
asserts that
![]() $\varphi (\cdot , \cdot , p)$
defines a total function which is non-trivial, cofinal and
$\varphi (\cdot , \cdot , p)$
defines a total function which is non-trivial, cofinal and
![]() $\Sigma _0$
-elementary. That is,
$\Sigma _0$
-elementary. That is,
Let
![]() $\vartheta (p, \kappa )$
assert that
$\vartheta (p, \kappa )$
assert that
![]() $\kappa $
is the critical point of j. So,
$\kappa $
is the critical point of j. So,
Then, by Proposition 3.1,
So denote by
![]() $\textrm {crit}_{\textit {p}}$
the (unique)
$\textrm {crit}_{\textit {p}}$
the (unique)
![]() $\kappa $
for which
$\kappa $
for which
![]() $\vartheta (p, \kappa )$
holds. Now fix p such that
$\vartheta (p, \kappa )$
holds. Now fix p such that
![]() $\textrm {crit}_{\textit {p}}$
is as small as possible, that is such that
$\textrm {crit}_{\textit {p}}$
is as small as possible, that is such that
Then, by elementarity,
But,
![]() because the critical point of the embedding defined by
because the critical point of the embedding defined by
![]() $\varphi (\cdot , \cdot , s)$
must be
$\varphi (\cdot , \cdot , s)$
must be
![]() $j(\textrm {crit}_{\textit {p}})$
, yielding a contradiction.⊣
$j(\textrm {crit}_{\textit {p}})$
, yielding a contradiction.⊣
We remark here that the main elements of the proof that there is no definable embedding of the universe into itself are that any such embedding has a critical point and being fully elementary can be expressed by a single sentence. Therefore, by using Gaifman’s original theorem, since the Collection Scheme wasn’t used in the proofs of Proposition 3.1 and Theorem 3.4, the above proof also shows that there is no non-trivial cofinal elementary embedding of a model of Zermelo plus a cumulative rank hierarchy of sets into itself which is definable from parameters. There are two obvious questions which appear here about whether or not the assumptions of cofinality and Collection were necessary in the proof that there is no definable embedding. That is;
Question 3.5. Are either of the following two statements consistent:
-
1. There exists a non-trivial elementary embedding
 which is definable from parameters where
which is definable from parameters where
 ?
? -
2. There exists a non-trivial, cofinal elementary embedding
 which is definable from parameters where
which is definable from parameters where
 ?
?
It has been proven in [Reference Gitman, Hamkins and Johnstone7] that one can have cofinal,
![]() $\Sigma _1$
-elementary embeddings of
$\Sigma _1$
-elementary embeddings of
![]() which are not
which are not
![]() $\Sigma _2$
-elementary, which is to say that Gaifman’s Theorem can fail without the Collection Scheme. Therefore proving Suzuki’s Theorem in either of these contexts would involve a different approach.
$\Sigma _2$
-elementary, which is to say that Gaifman’s Theorem can fail without the Collection Scheme. Therefore proving Suzuki’s Theorem in either of these contexts would involve a different approach.
4 Choosing from classes
In this short section we mention how one can apply Choice to set-length sequences of classes using the Collection Scheme. The standard way to do this in full ZFC is by using Scott’s trick to replace each class by the set of elements of least rank of that class. However, if
![]() is not a set for each
is not a set for each
![]() $\alpha $
then this may not be possible so we have to be slightly more careful in our approach.
$\alpha $
then this may not be possible so we have to be slightly more careful in our approach.
Let
![]() $\mu $
be an ordinal and suppose that we have a sequence of non-empty classes
$\mu $
be an ordinal and suppose that we have a sequence of non-empty classes
![]() $\langle \mathcal {C}_\alpha \colon \alpha \in \mu \rangle $
which are uniformly defined. This allows us to fix a formula
$\langle \mathcal {C}_\alpha \colon \alpha \in \mu \rangle $
which are uniformly defined. This allows us to fix a formula
![]() $\varphi (v_0, v_1)$
saying that
$\varphi (v_0, v_1)$
saying that
![]() $v_1 \in \mathcal {C}_{v_0}$
. Then, for each
$v_1 \in \mathcal {C}_{v_0}$
. Then, for each
![]() $\alpha \in \mu $
there is some set x such that
$\alpha \in \mu $
there is some set x such that
![]() $\varphi (\alpha , x)$
. So, by Collection, there is some set b such that for each
$\varphi (\alpha , x)$
. So, by Collection, there is some set b such that for each
![]() $\alpha \in \mu $
there is some
$\alpha \in \mu $
there is some
![]() $x \in b$
such that
$x \in b$
such that
![]() $\varphi (\alpha , x)$
. By well-ordering b, there is some cardinal
$\varphi (\alpha , x)$
. By well-ordering b, there is some cardinal
![]() $\tau $
and bijection
$\tau $
and bijection
![]() $h \colon \tau \leftrightarrow b$
. So for each
$h \colon \tau \leftrightarrow b$
. So for each
![]() $\alpha \in \mu $
we can define a choice function by taking
$\alpha \in \mu $
we can define a choice function by taking
![]() $x_\alpha \in \mathcal {C}_\alpha $
to be
$x_\alpha \in \mathcal {C}_\alpha $
to be
![]() $h(\gamma )$
for the least ordinal
$h(\gamma )$
for the least ordinal
![]() $\gamma \in \tau $
such that
$\gamma \in \tau $
such that
![]() $\varphi (\alpha , h(\gamma ))$
.
$\varphi (\alpha , h(\gamma ))$
.
For example, suppose that
![]() $S \subseteq \mu $
were a stationary set which was partitioned into
$S \subseteq \mu $
were a stationary set which was partitioned into
![]() $\tau < {\textrm {cf}}(\mu )$
many sets
$\tau < {\textrm {cf}}(\mu )$
many sets
![]() $\langle S_\alpha \colon \alpha \in \tau \rangle $
and one wanted to show that for some
$\langle S_\alpha \colon \alpha \in \tau \rangle $
and one wanted to show that for some
![]() $\alpha \in \tau $
,
$\alpha \in \tau $
,
![]() $S_\alpha $
was stationary. Arguing for a contradiction, suppose that none of the
$S_\alpha $
was stationary. Arguing for a contradiction, suppose that none of the
![]() $S_\alpha $
were stationary and for each
$S_\alpha $
were stationary and for each
![]() $\alpha \in \tau $
define
$\alpha \in \tau $
define
![]() $\mathcal {C}_\alpha $
to be the non-empty class of clubs
$\mathcal {C}_\alpha $
to be the non-empty class of clubs
![]() $D \subseteq \mu $
for which
$D \subseteq \mu $
for which
![]() $D \cap S_\alpha \neq \emptyset $
. By the above argument, we can choose a sequence of clubs
$D \cap S_\alpha \neq \emptyset $
. By the above argument, we can choose a sequence of clubs
![]() $ \langle D_\alpha \colon \alpha \in \tau \rangle $
such that for each
$ \langle D_\alpha \colon \alpha \in \tau \rangle $
such that for each
![]() $\alpha $
,
$\alpha $
,
![]() $D_\alpha \in \mathcal {C}_\alpha $
. Then
$D_\alpha \in \mathcal {C}_\alpha $
. Then
![]() $\bigcap _{\alpha \in \tau } D_\alpha \cap S = \emptyset $
yielding the required contradiction.
$\bigcap _{\alpha \in \tau } D_\alpha \cap S = \emptyset $
yielding the required contradiction.
Using this idea we are able to prove many useful classical results without much change from their standard proofs. For completeness, we give here two such
![]() results which we will then use in our proof of the Kunen inconsistency.
results which we will then use in our proof of the Kunen inconsistency.
Theorem 4.1 (Fodor).
Let
![]() $\mu $
be a regular cardinal,
$\mu $
be a regular cardinal,
![]() $S \subseteq \mu $
stationary and f a regressive function on S.Footnote
3
Then there exists some stationary set
$S \subseteq \mu $
stationary and f a regressive function on S.Footnote
3
Then there exists some stationary set
![]() $T \subseteq S$
and
$T \subseteq S$
and
![]() $\gamma \in \mu $
such that for all
$\gamma \in \mu $
such that for all
![]() $\alpha \in T$
,
$\alpha \in T$
,
![]() $f(\alpha ) = \gamma $
.
$f(\alpha ) = \gamma $
.
Proof. Assume for a contradiction that for each
![]() $\gamma \in \mu $
the set
$\gamma \in \mu $
the set
![]() $\{ \alpha \in S \colon f(\alpha ) = \gamma \}$
was non-stationary. Using the above comments, for each
$\{ \alpha \in S \colon f(\alpha ) = \gamma \}$
was non-stationary. Using the above comments, for each
![]() $\gamma \in \mu $
choose a club
$\gamma \in \mu $
choose a club
![]() $D_\gamma $
such that for each
$D_\gamma $
such that for each
![]() $\alpha $
in
$\alpha $
in
![]() $D_\gamma \cap S$
,
$D_\gamma \cap S$
,
![]() $f(\alpha )\neq \gamma $
. Let
$f(\alpha )\neq \gamma $
. Let
and note that this is club in
![]() $\mu $
. Therefore
$\mu $
. Therefore
![]() $S \cap D$
is stationary, so in particular non-empty, and for any
$S \cap D$
is stationary, so in particular non-empty, and for any
![]() $\alpha \in S \cap D$
and
$\alpha \in S \cap D$
and
![]() $\gamma \in \alpha $
,
$\gamma \in \alpha $
,
![]() $f(\alpha ) \neq \gamma $
. So
$f(\alpha ) \neq \gamma $
. So
![]() $f(\alpha ) \geq \alpha $
, contradicting the assumption that f was regressive.⊣
$f(\alpha ) \geq \alpha $
, contradicting the assumption that f was regressive.⊣
Definition 4.2. For cardinals
![]() $\delta < \mu $
let
$\delta < \mu $
let
![]() $S^\mu _\delta = \{ \alpha < \mu \colon {\textrm {cf}}(\alpha ) = \delta \}$
.
$S^\mu _\delta = \{ \alpha < \mu \colon {\textrm {cf}}(\alpha ) = \delta \}$
.
Theorem 4.3 (Solovay).
Suppose that
![]() $\mu $
is an uncountable, regular cardinal and
$\mu $
is an uncountable, regular cardinal and
![]() $S \subseteq S^\mu _\omega $
is stationary. Then there is a partition of S into
$S \subseteq S^\mu _\omega $
is stationary. Then there is a partition of S into
![]() $\mu $
many disjoint stationary sets.
$\mu $
many disjoint stationary sets.
Proof. First note that for each
![]() $\alpha \in S$
there is some increasing sequence of ordinals
$\alpha \in S$
there is some increasing sequence of ordinals
![]() $\langle t_n \colon n \in \omega \rangle $
cofinal in
$\langle t_n \colon n \in \omega \rangle $
cofinal in
![]() $\alpha $
. Therefore by the comments at the beginning of this section, for each
$\alpha $
. Therefore by the comments at the beginning of this section, for each
![]() $\alpha \in S$
choose an increasing sequence
$\alpha \in S$
choose an increasing sequence
![]() $\langle a^\alpha _n \colon n \in \omega \rangle $
cofinal in
$\langle a^\alpha _n \colon n \in \omega \rangle $
cofinal in
![]() $\alpha $
. Then, as in the usual proof, using our first example and the regularity of
$\alpha $
. Then, as in the usual proof, using our first example and the regularity of
![]() $\mu $
we can fix some
$\mu $
we can fix some
![]() $n \in \omega $
such that for each
$n \in \omega $
such that for each
![]() $\sigma \in \mu $
,
$\sigma \in \mu $
,
![]() $\{ \alpha \in S \colon a^\alpha _n \geq \sigma \}$
is stationary in
$\{ \alpha \in S \colon a^\alpha _n \geq \sigma \}$
is stationary in
![]() $\mu $
. Now define a regressive function
$\mu $
. Now define a regressive function
![]() $f \colon S \rightarrow \mu $
by
$f \colon S \rightarrow \mu $
by
![]() $f(\alpha ) = a^\alpha _n$
. Using Fodor’s Theorem, for each
$f(\alpha ) = a^\alpha _n$
. Using Fodor’s Theorem, for each
![]() $\sigma \in \mu $
fix some
$\sigma \in \mu $
fix some
![]() $S_\sigma $
stationary and
$S_\sigma $
stationary and
![]() $\gamma _\sigma \geq \sigma $
such that for all
$\gamma _\sigma \geq \sigma $
such that for all
![]() $\alpha \in S_\sigma $
,
$\alpha \in S_\sigma $
,
![]() $f(\alpha ) = \gamma _\sigma $
. Then if
$f(\alpha ) = \gamma _\sigma $
. Then if
![]() $\gamma _\sigma \neq \gamma _{\sigma '}$
,
$\gamma _\sigma \neq \gamma _{\sigma '}$
,
![]() $S_\sigma \cap S_{\sigma '} = \emptyset $
and, by the regularity of
$S_\sigma \cap S_{\sigma '} = \emptyset $
and, by the regularity of
![]() $\mu $
,
$\mu $
,
![]() $| \{ S_\sigma \colon \sigma \in \mu \} | = \mu ,$
which gives the required partition.⊣
$| \{ S_\sigma \colon \sigma \in \mu \} | = \mu ,$
which gives the required partition.⊣
5 Non-existence of embeddings
We are now in the position to prove that there is no non-trivial, cofinal elementary embedding j of
![]() with
with
![]() . This shall be done in two parts; first we shall show that Woodin’s proof of the Kunen inconsistency, which is the second proof of Theorem 23.12 in [Reference Kanamori13], goes through in
. This shall be done in two parts; first we shall show that Woodin’s proof of the Kunen inconsistency, which is the second proof of Theorem 23.12 in [Reference Kanamori13], goes through in
![]() under the additional assumption that
under the additional assumption that
![]() . Then we shall show, by modifying the coding from Theorem 2.2, that no cofinal embedding can exist in any model that sufficiently resembles
. Then we shall show, by modifying the coding from Theorem 2.2, that no cofinal embedding can exist in any model that sufficiently resembles
![]() .
.
In order to prove this formally we shall work in a subtheory of the second order version of
![]() which we shall denote as
which we shall denote as
![]() . Essentially this is the theory
. Essentially this is the theory
![]() along with a class predicate j for the elementary embedding and the assertion that the Collection and Separation Schemes hold when expanded to include formulae with this predicate. To be more precise;
along with a class predicate j for the elementary embedding and the assertion that the Collection and Separation Schemes hold when expanded to include formulae with this predicate. To be more precise;
Definition 5.1. Suppose that T is a first order set theory, M is a model of
![]() and j is a class predicate. We say that
and j is a class predicate. We say that
![]() if M satisfies the axiom schemes of T (for example Induction, Separation and Replacement / Collection / Reflection) in the language expanded to include j.
if M satisfies the axiom schemes of T (for example Induction, Separation and Replacement / Collection / Reflection) in the language expanded to include j.
Theorem 5.2. There is no non-trivial, elementary embedding
![]() such that
such that
![]() and
and
![]() .
.
Proof. Suppose for a contradiction that
![]() was a non-trivial elementary embedding with critical point
was a non-trivial elementary embedding with critical point
![]() $\kappa $
and let
$\kappa $
and let
![]() $\lambda = {\textrm {sup}} \{ j^n(\kappa ) \colon n \in \omega \}$
. Then
$\lambda = {\textrm {sup}} \{ j^n(\kappa ) \colon n \in \omega \}$
. Then
![]() $j(\lambda ) = \lambda $
and, since
$j(\lambda ) = \lambda $
and, since
![]() $\lambda ^+$
is definable as the least cardinal above
$\lambda ^+$
is definable as the least cardinal above
![]() $\lambda $
,
$\lambda $
,
![]() $j(\lambda ^+) = \lambda ^+$
. Now, using Theorem 4.3, let
$j(\lambda ^+) = \lambda ^+$
. Now, using Theorem 4.3, let
![]() $\langle S_\alpha : \alpha \in \kappa \rangle $
be a partition of
$\langle S_\alpha : \alpha \in \kappa \rangle $
be a partition of
![]() $S^{\lambda ^+}_\omega $
into
$S^{\lambda ^+}_\omega $
into
![]() $\kappa $
many disjoint stationary sets and let
$\kappa $
many disjoint stationary sets and let
![]() $S = \{ \langle \alpha , S_\alpha \rangle \colon \alpha \in \kappa \}$
. Then
$S = \{ \langle \alpha , S_\alpha \rangle \colon \alpha \in \kappa \}$
. Then
![]() $j(S) = \{ \langle \alpha , T_\alpha \rangle \colon \alpha \in j(\kappa ) \}$
and, by elementarity,
$j(S) = \{ \langle \alpha , T_\alpha \rangle \colon \alpha \in j(\kappa ) \}$
and, by elementarity,
![]() $\langle T_\alpha \colon \alpha \in j(\kappa ) \rangle $
is a partition of
$\langle T_\alpha \colon \alpha \in j(\kappa ) \rangle $
is a partition of
![]() $S^{\lambda ^+}_\omega $
into disjoint sets such that for each
$S^{\lambda ^+}_\omega $
into disjoint sets such that for each
![]() $\alpha $
$\alpha $
Also, we have that for each
![]() $\alpha \in \kappa $
,
$\alpha \in \kappa $
,
![]() $j(S_\alpha ) = T_\alpha $
. We claim that there is some
$j(S_\alpha ) = T_\alpha $
. We claim that there is some
![]() $\beta \in \kappa $
such that
$\beta \in \kappa $
such that
![]() $T_\kappa \cap S_\beta $
is stationary. For suppose not, then by our comments on choosing from set many classes, for each
$T_\kappa \cap S_\beta $
is stationary. For suppose not, then by our comments on choosing from set many classes, for each
![]() $\alpha $
we can fix a club
$\alpha $
we can fix a club
![]() $C_\alpha $
such that
$C_\alpha $
such that
![]() $T_\kappa \cap S_\alpha \cap C_\alpha = \emptyset $
. Letting
$T_\kappa \cap S_\alpha \cap C_\alpha = \emptyset $
. Letting
![]() $C = \bigcap _{\alpha \in \kappa } C_\alpha $
we must have that
$C = \bigcap _{\alpha \in \kappa } C_\alpha $
we must have that
contradicting the assumption that
![]() $T_\kappa $
was stationary. So fix
$T_\kappa $
was stationary. So fix
![]() $\beta $
such that
$\beta $
such that
![]() $T_\kappa \cap S_\beta $
is stationary. Now, let
$T_\kappa \cap S_\beta $
is stationary. Now, let
and note that U is closed under sequences of length
![]() $\omega $
. Therefore there exists some
$\omega $
. Therefore there exists some
![]() $\sigma \in U \cap T_\kappa \cap S_\beta $
. But then
$\sigma \in U \cap T_\kappa \cap S_\beta $
. But then
![]() $\sigma = j(\sigma ) \in j(S_\beta ) = T_\beta $
, contradicting the assumption that the
$\sigma = j(\sigma ) \in j(S_\beta ) = T_\beta $
, contradicting the assumption that the
![]() $T_\alpha $
were disjoint. Hence no such embedding can exist.⊣
$T_\alpha $
were disjoint. Hence no such embedding can exist.⊣
Remark 5.3. The above theorem did not require any assumption about j being cofinal or that
![]() was a set.
was a set.
Theorem 5.4. There is no non-trivial, cofinal,
![]() $\Sigma _0$
-elementary embedding
$\Sigma _0$
-elementary embedding
![]() such that
such that
![]() and
and
![]() .
.
Proof. Suppose for a contradiction that
![]() was a non-trivial, cofinal,
was a non-trivial, cofinal,
![]() $\Sigma _0$
-elementary embedding with critical point
$\Sigma _0$
-elementary embedding with critical point
![]() $\kappa $
and let
$\kappa $
and let
![]() $\lambda = {\textrm {sup}} \{ j^n(\kappa ) \colon n \in \omega \}$
. Note that, by an instance of Replacement in the language expanded to include the predicate j,
$\lambda = {\textrm {sup}} \{ j^n(\kappa ) \colon n \in \omega \}$
. Note that, by an instance of Replacement in the language expanded to include the predicate j,
![]() . Now there are two cases:
. Now there are two cases:
-
• Case 1:
 $\lambda ^+$
exists.
$\lambda ^+$
exists. -
• Case 2: For all
 , there is an injection
, there is an injection
 $f \colon x \rightarrow \lambda $
.
$f \colon x \rightarrow \lambda $
.
Case 1: Using Theorem 3.2, any such embedding must be fully elementary. Therefore, this is just a special case of Theorem 5.2.
Case 2: First note that by elementarity, since
![]() so is
so is
![]() for each
for each
![]() $n \in \omega $
and therefore
$n \in \omega $
and therefore
![]() . Note also that
. Note also that
![]() and, by the Well-Ordering Principle, for each
and, by the Well-Ordering Principle, for each
![]() there is a bijection
there is a bijection
Moreover, since there is an injection of x into
![]() $\lambda $
, we must have that
$\lambda $
, we must have that
![]() $| {\textrm {trcl}}(\{x\}) | \leq \lambda $
for each
$| {\textrm {trcl}}(\{x\}) | \leq \lambda $
for each
![]() . Now let
. Now let
Then
and therefore so is its Mostowski collapse, with
![]() ${\textrm {coll}}(C_{x, f}) = {\textrm {trcl}}(\{x\})$
. This means that for any x and bijection
${\textrm {coll}}(C_{x, f}) = {\textrm {trcl}}(\{x\})$
. This means that for any x and bijection
![]() $f \colon | {\textrm {trcl}}(\{x\}) | \rightarrow {\textrm {trcl}}(\{x\})$
,
$f \colon | {\textrm {trcl}}(\{x\}) | \rightarrow {\textrm {trcl}}(\{x\})$
,

That is, j is completely determined by its construction up to
. Now, let
and note that, since
, so is
Therefore, by defining
![]() $\varphi (\cdot , \cdot , i, \lambda )$
as
$\varphi (\cdot , \cdot , i, \lambda )$
as

we have that
![]() $\varphi (x, y, i, \lambda )$
holds if and only if
$\varphi (x, y, i, \lambda )$
holds if and only if
![]() $j(x) = y$
so j is definable from the parameters i and
$j(x) = y$
so j is definable from the parameters i and
![]() $\lambda $
, both of which lie in V, contradicting Theorem 3.4.⊣
$\lambda $
, both of which lie in V, contradicting Theorem 3.4.⊣
6 Removing the assumption that
 ${\mathrm {V}}_{{\mathrm {crit}}(\mathit {j})} \in {\mathrm {V}}$
${\mathrm {V}}_{{\mathrm {crit}}(\mathit {j})} \in {\mathrm {V}}$
Assuming that V satisfies the additional assumption of Dependent Choice of length
![]() $\mu $
for every infinite cardinal
$\mu $
for every infinite cardinal
![]() $\mu $
, we are able to remove the assumption that
$\mu $
, we are able to remove the assumption that
![]() . This will be done by first proving that, in this theory, every proper class must surject onto any given non-zero ordinal. In particular, for
. This will be done by first proving that, in this theory, every proper class must surject onto any given non-zero ordinal. In particular, for
![]() to be a proper class it is necessary for
to be a proper class it is necessary for
![]() to surject onto
to surject onto
![]() $j(\kappa )$
which we shall show cannot happen. Note that, in the standard ZFC case, the cardinality of
$j(\kappa )$
which we shall show cannot happen. Note that, in the standard ZFC case, the cardinality of
![]() is
is
![]() ${\textrm {crit}}(\textit {j})$
.
${\textrm {crit}}(\textit {j})$
.
In the ZF context the principle of Dependent Choice of length
![]() $\mu $
, for
$\mu $
, for
![]() $\mu $
an infinite cardinal is the following statement formulated by Lévy [Reference Lévy18].
$\mu $
an infinite cardinal is the following statement formulated by Lévy [Reference Lévy18].
Let S be a non-empty set and R a binary relation such that for every
![]() $\alpha \in \mu $
and every
$\alpha \in \mu $
and every
![]() $\alpha $
-sequence
$\alpha $
-sequence
![]() $s = \langle x_\beta : \beta \in \alpha \rangle $
of elements of S there exists some
$s = \langle x_\beta : \beta \in \alpha \rangle $
of elements of S there exists some
![]() $y \in S$
such that
$y \in S$
such that
![]() $s R y$
. Then there is a function
$s R y$
. Then there is a function
![]() $f : \mu \rightarrow S$
such that for every
$f : \mu \rightarrow S$
such that for every
![]() $\alpha \in \mu $
,
$\alpha \in \mu $
,
![]() $(f \operatorname {\mathrm {\upharpoonright }} \alpha ) R f(\alpha )$
.
$(f \operatorname {\mathrm {\upharpoonright }} \alpha ) R f(\alpha )$
.
In the more general
![]() context we want to consider a natural class version of this where S and R are replaced by definable classes. Such classes can be considered as the collection of sets x which satisfy
context we want to consider a natural class version of this where S and R are replaced by definable classes. Such classes can be considered as the collection of sets x which satisfy
![]() $\psi (x, u)$
for some formula
$\psi (x, u)$
for some formula
![]() $\psi $
. This leads to the definition of the
$\psi $
. This leads to the definition of the
![]() -Scheme as the following:
-Scheme as the following:
Let
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
be formulae and u be a set such that for some y,
$\psi $
be formulae and u be a set such that for some y,
![]() $\psi (y, u)$
and for every
$\psi (y, u)$
and for every
![]() $\alpha \in \mu $
and every
$\alpha \in \mu $
and every
![]() $\alpha $
-sequence
$\alpha $
-sequence
![]() $s = \langle x_\beta : \beta \in \alpha \rangle $
satisfying
$s = \langle x_\beta : \beta \in \alpha \rangle $
satisfying
![]() $\psi (x_\beta , u)$
for each
$\psi (x_\beta , u)$
for each
![]() $\beta $
, there is a z satisfying
$\beta $
, there is a z satisfying
![]() $\psi (z, u)$
and
$\psi (z, u)$
and
![]() $\varphi (\alpha , s, z, u)$
. Then there is a function f with domain
$\varphi (\alpha , s, z, u)$
. Then there is a function f with domain
![]() $\mu $
such that for each
$\mu $
such that for each
![]() $\alpha \in \mu \ \psi (f(\alpha ), u)$
and
$\alpha \in \mu \ \psi (f(\alpha ), u)$
and
![]() $\varphi (\alpha , f \operatorname {\mathrm {\upharpoonright }} \alpha , f(\alpha ), u)$
.
$\varphi (\alpha , f \operatorname {\mathrm {\upharpoonright }} \alpha , f(\alpha ), u)$
.
For
![]() $\mu = \aleph _0$
we shall refer to this concept as the DC-Scheme. An equivalent way to view the
$\mu = \aleph _0$
we shall refer to this concept as the DC-Scheme. An equivalent way to view the
![]() -Scheme is the assertion that if T is a tree that has no maximal element and is
-Scheme is the assertion that if T is a tree that has no maximal element and is
![]() $\mu $
-closed, that is to say every
$\mu $
-closed, that is to say every
![]() $\alpha $
-sequence of nodes in T has an upper bound, then T has a branch of order type
$\alpha $
-sequence of nodes in T has an upper bound, then T has a branch of order type
![]() $\mu $
. We note that, as with the set case, if
$\mu $
. We note that, as with the set case, if
![]() $\delta < \mu $
are infinite cardinals and
$\delta < \mu $
are infinite cardinals and
![]() holds then so does
holds then so does
![]() .
.
Proposition 6.1 [Reference Lévy18].
If
![]() $\delta < \mu $
are infinite cardinals then the
$\delta < \mu $
are infinite cardinals then the
![]() -Scheme implies the
-Scheme implies the
![]() -Scheme.
-Scheme.
Proof. Let
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
be formulae and u be a set such that for some y,
$\psi $
be formulae and u be a set such that for some y,
![]() $\psi (y, u)$
and for every
$\psi (y, u)$
and for every
![]() $\alpha \in \delta $
and every
$\alpha \in \delta $
and every
![]() $\alpha $
-sequence
$\alpha $
-sequence
![]() $s = \langle x_\beta \colon \beta \in \alpha \rangle $
satisfying
$s = \langle x_\beta \colon \beta \in \alpha \rangle $
satisfying
![]() $\psi (x_\beta , u)$
for each
$\psi (x_\beta , u)$
for each
![]() $\beta $
, there is a z satisfying
$\beta $
, there is a z satisfying
![]() $\psi (z, u)$
and
$\psi (z, u)$
and
![]() $\varphi (\alpha , s, z, u)$
. We define a new formula
$\varphi (\alpha , s, z, u)$
. We define a new formula
![]() $\vartheta $
extending
$\vartheta $
extending
![]() $\varphi $
to apply to any
$\varphi $
to apply to any
![]() $\alpha $
-sequence, s, for
$\alpha $
-sequence, s, for
![]() $\alpha \in \mu $
by
$\alpha \in \mu $
by
 $$ \begin{align*} &\vartheta(\alpha, s, z, u, \delta) \equiv \big( \alpha < \delta \wedge \forall \beta \in \alpha \ \psi(s(\beta), u) \wedge \varphi(\alpha, s, z, u) \big) \\[3pt] &\phantom{\big( \alpha < \delta \wedge \forall \beta \in \alpha \ \psi(s(\beta), u) \wedge \varphi(\alpha, s, z, u) \big)} \ \ \vee \big( \alpha \geq \delta \wedge \psi(z, u) \big). \end{align*} $$
$$ \begin{align*} &\vartheta(\alpha, s, z, u, \delta) \equiv \big( \alpha < \delta \wedge \forall \beta \in \alpha \ \psi(s(\beta), u) \wedge \varphi(\alpha, s, z, u) \big) \\[3pt] &\phantom{\big( \alpha < \delta \wedge \forall \beta \in \alpha \ \psi(s(\beta), u) \wedge \varphi(\alpha, s, z, u) \big)} \ \ \vee \big( \alpha \geq \delta \wedge \psi(z, u) \big). \end{align*} $$
Then for any function f with domain
![]() $\mu $
witnessing this instance of the
$\mu $
witnessing this instance of the
![]() -Scheme,
-Scheme,
![]() $f \operatorname {\mathrm {\upharpoonright }} \delta $
witnesses that
$f \operatorname {\mathrm {\upharpoonright }} \delta $
witnesses that
![]() holds for
holds for
![]() $\psi $
and
$\psi $
and
![]() $\varphi $
.⊣
$\varphi $
.⊣
An important strengthening of the Collection Scheme is the Reflection Principle which we define next.
Definition 6.2. The Reflection Principle is the assertion that for any formula
![]() $\varphi $
and set a there is a transitive set A such that
$\varphi $
and set a there is a transitive set A such that
![]() $a \subseteq A$
and
$a \subseteq A$
and
![]() $\varphi $
is absolute between A and the universe.
$\varphi $
is absolute between A and the universe.
The next pair of theorems show how this principle relates to Dependent Choice.
Theorem 6.3 [Reference Gitman, Hamkins and Johnstone7].
Over
![]() , the DC-Scheme is equivalent to the Reflection Principle.
, the DC-Scheme is equivalent to the Reflection Principle.
Theorem 6.4 [Reference Friedman, Gitman and Kanovei4].
The Reflection Principle is not provable in
![]() .
.
Remark 6.5. To see that the Reflection Principle implies the DC-Scheme, let T be some definable tree of height
![]() $\omega $
with no maximal element. This statement can be reflected to a transitive set M using the Reflection Principle which can then be well-ordered to provide the witnesses for an infinite branch.
$\omega $
with no maximal element. This statement can be reflected to a transitive set M using the Reflection Principle which can then be well-ordered to provide the witnesses for an infinite branch.
However, this argument does not go through for the
![]() -Scheme when
-Scheme when
![]() $\mu $
is an uncountable cardinal. The issue here is that the transitive set M need not be closed under infinite sequences definable in the full universe. Therefore, when we reflect the tree it need no longer be the case that the tree is closed under sequences of length less than
$\mu $
is an uncountable cardinal. The issue here is that the transitive set M need not be closed under infinite sequences definable in the full universe. Therefore, when we reflect the tree it need no longer be the case that the tree is closed under sequences of length less than
![]() $\mu $
.Footnote
4
$\mu $
.Footnote
4
This leads to the theory that we shall work in throughout this section,
Definition 6.6. Let
![]() denote the theory
denote the theory
![]() plus the
plus the
![]() -Scheme for every cardinal
-Scheme for every cardinal
![]() $\mu $
.
$\mu $
.
Theorem 6.7. Suppose that
![]() for
for
![]() $\mu $
an infinite cardinal. Then for any proper class
$\mu $
an infinite cardinal. Then for any proper class
![]() $\mathcal {C}$
, which is definable over V, there is a subset b of
$\mathcal {C}$
, which is definable over V, there is a subset b of
![]() $\mathcal {C}$
of cardinality
$\mathcal {C}$
of cardinality
![]() $\mu $
.
$\mu $
.
Proof. Let
![]() $\mathcal {C} = \{ x \colon \psi (x) \}$
be a proper class. We shall in fact prove the equivalent statement that for any
$\mathcal {C} = \{ x \colon \psi (x) \}$
be a proper class. We shall in fact prove the equivalent statement that for any
![]() $\nu \leq \mu $
there is a subset b of
$\nu \leq \mu $
there is a subset b of
![]() $\mathcal {C}$
and a bijection between b and
$\mathcal {C}$
and a bijection between b and
![]() $\nu $
. Suppose for a contradiction that this were not the case and let
$\nu $
. Suppose for a contradiction that this were not the case and let
![]() $\gamma $
be the least ordinal for which no such subset of size
$\gamma $
be the least ordinal for which no such subset of size
![]() $\gamma $
exists. It is obvious that
$\gamma $
exists. It is obvious that
![]() $\gamma $
must be an infinite cardinal. Let
$\gamma $
must be an infinite cardinal. Let
![]() $\varphi (\alpha , s, y)$
be the statement that s is a sequence of length
$\varphi (\alpha , s, y)$
be the statement that s is a sequence of length
![]() $\alpha $
and
$\alpha $
and
![]() ${\textrm {ran}}(s) \cup \{y\}$
is a subset of
${\textrm {ran}}(s) \cup \{y\}$
is a subset of
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
![]() $y \not \in {\textrm {ran}}(s)$
. Then, by assumption, for every
$y \not \in {\textrm {ran}}(s)$
. Then, by assumption, for every
![]() $\alpha \in \gamma $
there is a sequence of elements of
$\alpha \in \gamma $
there is a sequence of elements of
![]() $\mathcal {C}$
of length
$\mathcal {C}$
of length
![]() $\alpha $
. Also, since
$\alpha $
. Also, since
![]() $\mathcal {C}$
is a proper class, if s is an
$\mathcal {C}$
is a proper class, if s is an
![]() $\alpha $
length sequence from
$\alpha $
length sequence from
![]() $\mathcal {C}$
then there is some
$\mathcal {C}$
then there is some
![]() $y \in \mathcal {C}$
which is not in s so the hypothesis of
$y \in \mathcal {C}$
which is not in s so the hypothesis of
![]() is satisfied. Therefore, by
is satisfied. Therefore, by
![]() , there is a function f with domain
, there is a function f with domain
![]() $\gamma $
and whose range gives a subset of
$\gamma $
and whose range gives a subset of
![]() $\mathcal {C}$
of cardinality
$\mathcal {C}$
of cardinality
![]() $\gamma $
, giving us our desired contradiction.⊣
$\gamma $
, giving us our desired contradiction.⊣
Corollary 6.8. Suppose that
![]() . Then for any proper class
. Then for any proper class
![]() $\mathcal {C}$
which is definable over V and any non-zero ordinal
$\mathcal {C}$
which is definable over V and any non-zero ordinal
![]() $\gamma $
there is a definable surjection of
$\gamma $
there is a definable surjection of
![]() $\mathcal {C}$
onto
$\mathcal {C}$
onto
![]() $\gamma $
.
$\gamma $
.
We can now prove that if j is a non-trivial elementary embedding from V to some class
![]() then
then
![]() .
.
Lemma 6.9. Suppose that
![]() ,
,
![]() and
and
![]() is a non-trivial elementary embedding with critical point
is a non-trivial elementary embedding with critical point
![]() $\kappa $
. Then for any
$\kappa $
. Then for any
![]() $\alpha \in \kappa + 1$
,
$\alpha \in \kappa + 1$
,
![]() .
.
Proof. This is proven by induction on
![]() $\alpha \in \kappa + 1$
. Clearly limit cases follow by an instance of Collection so it suffices to prove that for
$\alpha \in \kappa + 1$
. Clearly limit cases follow by an instance of Collection so it suffices to prove that for
![]() $\alpha \in \kappa $
, if
$\alpha \in \kappa $
, if
![]() then so is
then so is
![]() . First note that j fixes every set of rank less than
. First note that j fixes every set of rank less than
![]() $\kappa $
so
$\kappa $
so
![]() is the identity. Now suppose for sake of a contradiction that
is the identity. Now suppose for sake of a contradiction that
![]() was a proper class. Then, by Corollary 6.8, we could fix a set
was a proper class. Then, by Corollary 6.8, we could fix a set
![]() and a surjection
and a surjection
So, by elementarity, there is a surjection
in M. However, since
![]() ,
,
![]() $j(b)$
is also a subset of
$j(b)$
is also a subset of
![]() and for any
and for any
![]() $x \in j(b)$
,
$x \in j(b)$
,
![]() $j(x) = x$
. Therefore,
$j(x) = x$
. Therefore,
and hence
![]() $b = j(b)$
. Then, for any
$b = j(b)$
. Then, for any
![]() $x \in b$
,
$x \in b$
,
so
![]() $j(h) = h$
. But this then contradicts the assumption that
$j(h) = h$
. But this then contradicts the assumption that
![]() $j(h)$
was a surjection onto
$j(h)$
was a surjection onto
![]() $j(\kappa ).$
Hence
$j(\kappa ).$
Hence
![]() must be a set in V as required.⊣
must be a set in V as required.⊣
Combining this result with Theorem 5.4 gives the Kunen inconsistency for the theory
![]()
Corollary 6.10. There is no non-trivial, cofinal,
![]() $\Sigma _0$
-elementary embedding
$\Sigma _0$
-elementary embedding
![]() such that
such that
![]() .
.
However this leaves open the question as to whether or not this result is provable without relying on
![]() , namely;
, namely;
Question 6.11. Is the existence of a non-trivial, cofinal,
![]() $\Sigma _0$
-elementary embedding
$\Sigma _0$
-elementary embedding
![]() such that
such that
![]() inconsistent?
inconsistent?
The stumbling block that one needs to overcome appears to be the following:
Question 6.12. Suppose that
![]() ,
,
![]() and
and
![]() is a non-trivial elementary embedding. Is
is a non-trivial elementary embedding. Is
![]() ? Is
? Is
![]() ?Footnote
5
?Footnote
5
7 Collection in symmetric models
The important tool from the previous section was the fact that in models of
![]() proper classes are “big”. That is, given any non-zero ordinal, any proper class surjects onto that ordinal. This property is also a feature of models of ZF as shown by the following result:
proper classes are “big”. That is, given any non-zero ordinal, any proper class surjects onto that ordinal. This property is also a feature of models of ZF as shown by the following result:
Proposition 7.1. Under ZF, there is a surjection from any proper class onto any non-zero ordinal.
Proof. Given a proper class
![]() $\mathcal {C}$
, define
$\mathcal {C}$
, define
Then S must be unbounded in the ordinals so, given an ordinal
![]() $\alpha $
, we can take the first
$\alpha $
, we can take the first
![]() $\alpha $
many elements of S,
$\alpha $
many elements of S,
![]() $\{ \gamma _\beta : \beta \in \alpha \}$
. Then
$\{ \gamma _\beta : \beta \in \alpha \}$
. Then
 $$ \begin{align*} f(x) = \begin{cases} \beta, & \textit{if} \ {\textrm{rank}}(x) = \gamma_\beta, \\ 0, &\textit{otherwise}, \end{cases} \end{align*} $$
$$ \begin{align*} f(x) = \begin{cases} \beta, & \textit{if} \ {\textrm{rank}}(x) = \gamma_\beta, \\ 0, &\textit{otherwise}, \end{cases} \end{align*} $$
defines a surjection of
![]() $\mathcal {C}$
onto
$\mathcal {C}$
onto
![]() $\alpha $
.⊣
$\alpha $
.⊣
On the other hand, we have the following theorem from [Reference Gitman, Hamkins and Johnstone7]:
Theorem 7.2 [Reference Gitman, Hamkins and Johnstone7].
Suppose that
![]() ,
,
![]() $\kappa $
is a regular cardinal with
$\kappa $
is a regular cardinal with
![]() $2^\omega < \aleph _\kappa $
and that
$2^\omega < \aleph _\kappa $
and that
![]() $G \subseteq {\mathrm{Add}}(\omega , \aleph _\kappa )$
is
$G \subseteq {\mathrm{Add}}(\omega , \aleph _\kappa )$
is
![]() If
If
![]() where
where
![]() $G_\gamma = G \cap {\mathrm{Add}}(\omega , \aleph _\gamma )$
,
$G_\gamma = G \cap {\mathrm{Add}}(\omega , \aleph _\gamma )$
,
![]() $($
that is
$($
that is
![]() $G_\gamma $
is the first
$G_\gamma $
is the first
![]() $\aleph _\gamma $
many of the Cohen reals added by
$\aleph _\gamma $
many of the Cohen reals added by
![]() $G)$
then
$G)$
then
![]() has the same cardinals as V and the
has the same cardinals as V and the
![]() -Scheme holds in W for all
-Scheme holds in W for all
![]() $\alpha < \kappa $
, but the
$\alpha < \kappa $
, but the
![]() -Scheme and the Reflection Principle fail.
-Scheme and the Reflection Principle fail.
Since V will have the same cardinals as
![]() , that is the full extension by all
, that is the full extension by all
![]() $\aleph _\kappa $
many reals, in
$\aleph _\kappa $
many reals, in
![]() and therefore there is no surjection of
and therefore there is no surjection of
![]() $\mathcal {P}(\omega )$
onto
$\mathcal {P}(\omega )$
onto
![]() $\aleph _{\kappa + 1}$
. Hence there is no such surjection in W, so W is a model of
$\aleph _{\kappa + 1}$
. Hence there is no such surjection in W, so W is a model of
![]() and the
and the
![]() -scheme for all
-scheme for all
![]() $\alpha \in \kappa $
in which
$\alpha \in \kappa $
in which
![]() $\mathcal {P}(\omega )$
is a proper class which is not big.
$\mathcal {P}(\omega )$
is a proper class which is not big.
So it seems natural to ask which sub-theories of ZFC also prove this feature. While we shall not answer this question here, the following results show the difficulty in coming up with a counterexample in the theory
![]() .
.
One candidate for a counterexample in this theory is an amorphous class where:
Definition 7.3. A class A is said to be amorphous if it is infinite but not the disjoint union of two infinite subclasses. Namely, if
![]() $A = B \cup C$
and
$A = B \cup C$
and
![]() $B \cap C = \emptyset $
then either B or C must be a finite set.
$B \cap C = \emptyset $
then either B or C must be a finite set.
Now one could imagine having a set
![]() with
with
![]() such that M believes that A is an amorphous class. Then A could not surject onto
such that M believes that A is an amorphous class. Then A could not surject onto
![]() $\omega $
since if f were such a surjection,
$\omega $
since if f were such a surjection,
![]() $\{ x \in A : f(x) \textit { is even} \}$
and
$\{ x \in A : f(x) \textit { is even} \}$
and
![]() $\{ x \in A : f(x) \textit { is odd} \}$
would be a partition of A into two infinite classes. However, we shall show that such a situation can never arise because it is inconsistent with
$\{ x \in A : f(x) \textit { is odd} \}$
would be a partition of A into two infinite classes. However, we shall show that such a situation can never arise because it is inconsistent with
![]() to have a definable amorphous class. In fact, the analysis will show that a symmetric submodel of a pretame class forcing will not in general satisfy the Collection Scheme. To begin with we give the basics of symmetric extensions.
to have a definable amorphous class. In fact, the analysis will show that a symmetric submodel of a pretame class forcing will not in general satisfy the Collection Scheme. To begin with we give the basics of symmetric extensions.
7.1 Symmetric extensions
When talking about symmetric extensions we shall follow the notation of Karagila, which can be found in papers such as [Reference Karagila14, Reference Karagila15 ]. The purpose of symmetric extensions is to find a suitable submodel of a generic extension of ZFC in which Choice fails. This allows us to build objects such as Dedekind-finite sets and amorphous sets whose existence would contradict the Axiom of Choice while still using Choice in the ground model to control what happens.
Notation 7.4. Given a set of
![]() $\mathbb {P}$
-names
$\mathbb {P}$
-names
![]() $\{ \dot {x}_i \colon i \in I \}$
let
$\{ \dot {x}_i \colon i \in I \}$
let
![]() $\{ \dot {x}_i \colon i \in I \}^{\bullet }$
denote the
$\{ \dot {x}_i \colon i \in I \}^{\bullet }$
denote the
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() .
.
Now, given a forcing notion
![]() $\mathbb {P}$
and automorphism
$\mathbb {P}$
and automorphism
![]() $\pi $
of
$\pi $
of
![]() $\mathbb {P}$
,
$\mathbb {P}$
,
![]() $\pi $
can be extended to
$\pi $
can be extended to
![]() $\mathbb {P}$
-names by the following recursion:
$\mathbb {P}$
-names by the following recursion:
For
![]() $\mathcal {G}$
a group of automorphisms of
$\mathcal {G}$
a group of automorphisms of
![]() $\mathbb {P}$
we say that
$\mathbb {P}$
we say that
![]() $\mathcal {F}$
is a normal filter of subgroups over
$\mathcal {F}$
is a normal filter of subgroups over
![]() $\mathcal {G}$
if:
$\mathcal {G}$
if:
-
•
 $\mathcal {F}$
is a non-empty family of subgroups of
$\mathcal {F}$
is a non-empty family of subgroups of
 $\mathcal {G}$
.
$\mathcal {G}$
. -
•
 $\mathcal {F}$
is closed under finite intersections and supergroups.
$\mathcal {F}$
is closed under finite intersections and supergroups. -
• (Normality) For any
 $H \in \mathcal {F}$
and
$H \in \mathcal {F}$
and
 $\pi \in \mathcal {G}$
,
$\pi \in \mathcal {G}$
,
 $\pi H \pi ^{-1} \in \mathcal {F}$
.
$\pi H \pi ^{-1} \in \mathcal {F}$
.
A symmetric system is then a triple
![]() $\langle \mathbb {P}, \mathcal {G}, \mathcal {F} \rangle $
such that
$\langle \mathbb {P}, \mathcal {G}, \mathcal {F} \rangle $
such that
![]() $\mathbb {P}$
is a notion of forcing,
$\mathbb {P}$
is a notion of forcing,
![]() $\mathcal {G}$
is a group of automorphisms of
$\mathcal {G}$
is a group of automorphisms of
![]() $\mathbb {P}$
and
$\mathbb {P}$
and
![]() $\mathcal {F}$
is a normal filter of subgroups over
$\mathcal {F}$
is a normal filter of subgroups over
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
We also fix the following notation:
-
• The stabaliser of
 $\dot {x}$
under
$\dot {x}$
under
 $\mathcal {G}$
is
$\mathcal {G}$
is
 ${\textrm {sym}}_{\mathcal {G}} (\dot {x}) = \{ \pi \in \mathcal {G} \colon \pi \dot {x} = \dot {x} \}$
.
${\textrm {sym}}_{\mathcal {G}} (\dot {x}) = \{ \pi \in \mathcal {G} \colon \pi \dot {x} = \dot {x} \}$
. -
•
 $\dot {x}$
is said to be
$\dot {x}$
is said to be
 $\mathcal {F}$
-symmetric when
$\mathcal {F}$
-symmetric when
 ${\textrm {sym}}_{\mathcal {G}} (\dot {x}) \in \mathcal {F}$
.
${\textrm {sym}}_{\mathcal {G}} (\dot {x}) \in \mathcal {F}$
. -
•
 $\dot {x}$
is said to be hereditarily
$\dot {x}$
is said to be hereditarily
 $\mathcal {F}$
-symmetric when it is
$\mathcal {F}$
-symmetric when it is
 $\mathcal {F}$
-symmetric and for any
$\mathcal {F}$
-symmetric and for any
 $\langle p, \dot {y} \rangle $
in
$\langle p, \dot {y} \rangle $
in
 $\dot {x}$
,
$\dot {x}$
,
 $\dot {y}$
is also hereditarily
$\dot {y}$
is also hereditarily
 $\mathcal {F}$
-symmetric.
$\mathcal {F}$
-symmetric. -
•
 denotes the class of hereditarily
denotes the class of hereditarily
 $\mathcal {F}$
-symmetric names.
$\mathcal {F}$
-symmetric names.
We then have the following two theorems which summarise the important consequences of this construction and can be found in Chapter 15 of [Reference Jech12].
Lemma 7.5 (The Symmetry Lemma).
For any
![]() $p \in \mathbb {P}$
, automorphism
$p \in \mathbb {P}$
, automorphism
![]() $\pi $
of
$\pi $
of
![]() $\mathbb {P}$
, formula
$\mathbb {P}$
, formula
![]() $\varphi (v)$
of the forcing language and
$\varphi (v)$
of the forcing language and
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\dot {x}$
,
$\dot {x}$
,
Theorem 7.6. If M is a transitive model of
![]() ,
,
![]() $\langle \mathbb {P}, \mathcal {G}, \mathcal {F} \rangle $
is a symmetric system and
$\langle \mathbb {P}, \mathcal {G}, \mathcal {F} \rangle $
is a symmetric system and
![]() $G \subseteq \mathbb {P}$
is a generic filter then
$G \subseteq \mathbb {P}$
is a generic filter then
![]() is a transitive model of ZF with
is a transitive model of ZF with
![]() .
.
7.2 Class forcing
In order to describe our desired models, we shall need to do a relatively simple class forcing. Because class forcing is not the main goal of this paper, we shall only briefly sketch the construction and refer the reader to works such as [Reference Friedman3], [Reference Holy, Krapf, Lücke, Njegomir and Schlicht9] or [Reference Holy, Krapf and Schlicht10] for more details on how to formally define class forcing.
As in set forcing, when trying to formalise the theory of class forcing one often works in a countable, transitive model of some second order theory such as
![]() . Such a model will be of the form
. Such a model will be of the form
![]() where M denotes the sets of the model and
where M denotes the sets of the model and
![]() $\mathcal {C}$
the classes. However, primarily for ease of notation, we shall repeatedly only talk about the first order part of the theory, noting that if M is a set model of
$\mathcal {C}$
the classes. However, primarily for ease of notation, we shall repeatedly only talk about the first order part of the theory, noting that if M is a set model of
![]() and
and
![]() $\mathcal {C}$
is the collection of classes definable over M then
$\mathcal {C}$
is the collection of classes definable over M then
![]() is a model of
is a model of
![]() . We shall say that a class
. We shall say that a class
![]() $\dot {\Gamma }$
is a
$\dot {\Gamma }$
is a
![]() $\mathbb {P}$
-name if every element of
$\mathbb {P}$
-name if every element of
![]() $\dot {\Gamma }$
is of the form
$\dot {\Gamma }$
is of the form
![]() $\langle \dot {x}, p \rangle $
where
$\langle \dot {x}, p \rangle $
where
![]() $\dot {x}$
is a
$\dot {x}$
is a
![]() $\mathbb {P}$
-name and
$\mathbb {P}$
-name and
![]() $p \in \mathbb {P}$
. We then define
$p \in \mathbb {P}$
. We then define
![]() to be the collection of
to be the collection of
![]() $\mathbb {P}$
-names which are elements of M and define
$\mathbb {P}$
-names which are elements of M and define
![]() $\mathcal {C}^{\mathbb {P}}$
as those names which are in
$\mathcal {C}^{\mathbb {P}}$
as those names which are in
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
Essentially, the question is which properties of set forcing are still true when the partial order,
![]() $\mathbb {P}$
, is now assumed to be a proper class. Here one immediately runs into a problem when trying to prove the forcing theorem which comprises of two parts; truth and definability. The definability lemma is the assertion that the forcing relation is definable in the ground model and the truth lemma is that anything true in the generic extension is forced to be true by an element of the generic. However, as shown in [Reference Holy, Krapf, Lücke, Njegomir and Schlicht9], given any countable, transitive model of
$\mathbb {P}$
, is now assumed to be a proper class. Here one immediately runs into a problem when trying to prove the forcing theorem which comprises of two parts; truth and definability. The definability lemma is the assertion that the forcing relation is definable in the ground model and the truth lemma is that anything true in the generic extension is forced to be true by an element of the generic. However, as shown in [Reference Holy, Krapf, Lücke, Njegomir and Schlicht9], given any countable, transitive model of
![]() there is a class forcing notion which does not satisfy the forcing theorem for atomic formulae. In fact, it is shown in [Reference Gitman, Hamkins, Holy, Schlicht and Williams6] that, over GB with a global well-order, the statement that the forcing theorem holds for any class forcing is equivalent to elementary transfinite recursion for any recursion of length Ord.
there is a class forcing notion which does not satisfy the forcing theorem for atomic formulae. In fact, it is shown in [Reference Gitman, Hamkins, Holy, Schlicht and Williams6] that, over GB with a global well-order, the statement that the forcing theorem holds for any class forcing is equivalent to elementary transfinite recursion for any recursion of length Ord.
Moreover, even if a class forcing satisfies the forcing theorem it is not always the case that
![]() will be preserved in any generic extension. The simplest such example is
will be preserved in any generic extension. The simplest such example is
![]() which generically adds a function collapsing the ordinals onto
which generically adds a function collapsing the ordinals onto
![]() $\omega $
. However, there is a well known collection of class forcings which both satisfy the forcing theorem and preserve all of the axioms of
$\omega $
. However, there is a well known collection of class forcings which both satisfy the forcing theorem and preserve all of the axioms of
![]() . This property was first defined by Stanley and, while such forcings are normally characterised combinatorially, for our purposes we shall use a simpler but less enlightening definition which one can prove is equivalent.
. This property was first defined by Stanley and, while such forcings are normally characterised combinatorially, for our purposes we shall use a simpler but less enlightening definition which one can prove is equivalent.
Definition 7.7 (Stanley).
Let
![]() $\mathbb {M}$
be a model of
$\mathbb {M}$
be a model of
![]() . A class forcing
. A class forcing
![]() $\mathbb {P}$
is said to be pretame for
$\mathbb {P}$
is said to be pretame for
![]() $\mathbb {M}$
if, for any generic filter
$\mathbb {M}$
if, for any generic filter
![]() $G \subseteq \mathbb {P}$
,
$G \subseteq \mathbb {P}$
,
![]() $\mathbb {M}[G]$
satisfies
$\mathbb {M}[G]$
satisfies
![]() .
.
The class forcing we shall consider is
![]() , the forcing to add a proper class of Cohen reals. It can be proven that this satisfies the forcing theorem because it is ordinal approachable by projections,Footnote
6
that is to say it can be written as a continuous, increasing union of set-sized forcings,
, the forcing to add a proper class of Cohen reals. It can be proven that this satisfies the forcing theorem because it is ordinal approachable by projections,Footnote
6
that is to say it can be written as a continuous, increasing union of set-sized forcings,
![]() .
.
Theorem 7.8 [Reference Holy, Krapf, Lücke, Njegomir and Schlicht9].
If
![]() $\mathbb {P}$
is ordinal approachable by projections then
$\mathbb {P}$
is ordinal approachable by projections then
![]() $\mathbb {P}$
satisfies the forcing theorem.
$\mathbb {P}$
satisfies the forcing theorem.
While this property in itself does not ensure that the forcing is pretame, it allows us to use an equivalent characterisation of pretameness from [Reference Holy, Krapf and Schlicht10]:
Theorem 7.9 [Reference Holy, Krapf and Schlicht10].
Suppose that
![]() is a model of GB and
is a model of GB and
![]() $\mathbb {P}$
is a class forcing notion for
$\mathbb {P}$
is a class forcing notion for
![]() $\mathbb {M}$
which satisfies the forcing theorem. Then
$\mathbb {M}$
which satisfies the forcing theorem. Then
![]() $\mathbb {P}$
is pretame if and only if there is no set
$\mathbb {P}$
is pretame if and only if there is no set
![]() , name
, name
![]() $\dot {F} \in \mathcal {C}^{\mathbb {P}}$
and condition
$\dot {F} \in \mathcal {C}^{\mathbb {P}}$
and condition
![]() $p \in \mathbb {P}$
such that
$p \in \mathbb {P}$
such that
![]()
Theorem 7.10. Suppose that
![]() is a model of GB + AC and
is a model of GB + AC and
![]() $\mathbb {P}$
is a class forcing notion for
$\mathbb {P}$
is a class forcing notion for
![]() $\mathbb {M}$
which satisfies the forcing theorem. If
$\mathbb {M}$
which satisfies the forcing theorem. If
![]() $\mu $
is an uncountable cardinal in
$\mu $
is an uncountable cardinal in
![]() $\mathbb {M}$
and
$\mathbb {M}$
and
![]() $\mathbb {P}$
satisfies the
$\mathbb {P}$
satisfies the
![]() $\mu $
-cc then
$\mu $
-cc then
![]() $\mathbb {P}$
is pretame.
$\mathbb {P}$
is pretame.
Proof. This will be proven by a variation on a standard set forcing result which uses the
![]() $\mu $
-cc to approximate functions in the extension:
$\mu $
-cc to approximate functions in the extension:
Claim 7.11. Suppose that
![]() and
and
![]() is a class function in
is a class function in
![]() $\mathbb {M}[G]$
. Then there exists some
$\mathbb {M}[G]$
. Then there exists some
![]() such that for all
such that for all
![]() $x \in a$
,
$x \in a$
,
![]() $F(x) \in f(x)$
and
$F(x) \in f(x)$
and
![]() .
.
To prove the claim, let
![]() $\dot {F}$
be a name for F and take p such that
$\dot {F}$
be a name for F and take p such that
. Next, for each
![]() $x \in a$
, let
$x \in a$
, let
Now suppose that for some
![]() $x \in a$
,
$x \in a$
,
![]() $f(x)$
did not have cardinality less than
$f(x)$
did not have cardinality less than
![]() $\mu $
. By using Collection and set sized Choice, we can choose a subset Y of
$\mu $
. By using Collection and set sized Choice, we can choose a subset Y of
![]() $f(x)$
of size
$f(x)$
of size
![]() $\mu $
. Then for each
$\mu $
. Then for each
![]() $\alpha \in Y$
we can choose
$\alpha \in Y$
we can choose
![]() $q_\alpha \leq p$
such that
$q_\alpha \leq p$
such that
![]() $q_\alpha \Vdash \dot {F}(\check {x}) = \check {\alpha }$
. But then this must be an antichain of size
$q_\alpha \Vdash \dot {F}(\check {x}) = \check {\alpha }$
. But then this must be an antichain of size
![]() $\mu $
contradicting the assumption of
$\mu $
contradicting the assumption of
![]() $\mu $
-cc.
$\mu $
-cc.
Using the claim, we have that if
![]() ,
,
![]() $\dot {F} \in \mathcal {C}^{\mathbb {P}}$
and
$\dot {F} \in \mathcal {C}^{\mathbb {P}}$
and
![]() $p \in \mathbb {P}$
are such that
$p \in \mathbb {P}$
are such that
![]() then, taking f from the conclusion of the claim,
then, taking f from the conclusion of the claim,
![]() $\delta = {\textrm {sup}} \{ {\textrm {sup}}(f(x)) : x \in a \}$
is an ordinal. Therefore
$\delta = {\textrm {sup}} \{ {\textrm {sup}}(f(x)) : x \in a \}$
is an ordinal. Therefore
So, in particular, p cannot force the function to be cofinal which implies that
![]() $\mathbb {P}$
is pretame by Theorem 7.9.⊣
$\mathbb {P}$
is pretame by Theorem 7.9.⊣
7.3 Breaking collection
We can now produce our class symmetric systems. Solely for simplicity, let
![]() $\mathbb {M}$
be a countable, transitive model of GB + AC + CH. The first model we give is a symmetric system to add an amorphous class consisting of sets of Cohen reals. A detailed account of the set version of this forcing can be found as Exercise 8.13.1 of [Reference Drake and Singh2] which serves as the basis for our construction.
$\mathbb {M}$
be a countable, transitive model of GB + AC + CH. The first model we give is a symmetric system to add an amorphous class consisting of sets of Cohen reals. A detailed account of the set version of this forcing can be found as Exercise 8.13.1 of [Reference Drake and Singh2] which serves as the basis for our construction.
Let
be the poset which adds
many
![]() $\omega $
-blocks of Cohen reals. Now, for
$\omega $
-blocks of Cohen reals. Now, for
![]() $\pi ^0$
a permutation of Ord and
$\pi ^0$
a permutation of Ord and
a collection of permutations of
![]() $\omega $
let
$\omega $
let
![]() $\pi $
be the permutation
$\pi $
be the permutation
and let
![]() $\mathcal {G}$
be the class of permutations defined in this way. This is known as the wreath product of the permutations of Ord and the permutations of
$\mathcal {G}$
be the class of permutations defined in this way. This is known as the wreath product of the permutations of Ord and the permutations of
![]() $\omega $
. Then let
$\omega $
. Then let
![]() $\mathcal {F}$
be the filter generated by
$\mathcal {F}$
be the filter generated by
![]() ${\textrm {fix}}(E) \operatorname {\mathrm {:=}} \{ \pi \in \mathcal {G} : \pi \operatorname {\mathrm {\upharpoonright }} E = {\textrm {id}} \}$
for finite sets
${\textrm {fix}}(E) \operatorname {\mathrm {:=}} \{ \pi \in \mathcal {G} : \pi \operatorname {\mathrm {\upharpoonright }} E = {\textrm {id}} \}$
for finite sets
We can extend
![]() $\pi $
to
$\pi $
to
![]() $\mathbb {P}$
by
$\mathbb {P}$
by
So the idea is that elements of
![]() $\mathcal {G}$
first permute the
$\mathcal {G}$
first permute the
![]() $\omega $
-blocks of reals and then permute within the blocks.
$\omega $
-blocks of reals and then permute within the blocks.
Now define
-
•
 $\dot {t}_{(\alpha , n)} \operatorname {\mathrm {:=}} \{ \langle \check {m}, p \rangle \colon p \in \mathbb {P} \ \wedge \ p(\alpha , n, m) = 1 \}$
. This is the canonical name for the Cohen real generated by
$\dot {t}_{(\alpha , n)} \operatorname {\mathrm {:=}} \{ \langle \check {m}, p \rangle \colon p \in \mathbb {P} \ \wedge \ p(\alpha , n, m) = 1 \}$
. This is the canonical name for the Cohen real generated by
 $\mathbb {P}$
restricted to the co-ordinate
$\mathbb {P}$
restricted to the co-ordinate
 $(\alpha , n)$
.
$(\alpha , n)$
. -
•
 $\dot {T}_\alpha \operatorname {\mathrm {:=}} \{\dot {t}_{(\alpha , n)} \colon n \in \omega \}^{\bullet }$
to be a name for the
$\dot {T}_\alpha \operatorname {\mathrm {:=}} \{\dot {t}_{(\alpha , n)} \colon n \in \omega \}^{\bullet }$
to be a name for the
 $\alpha ^{th} \ \omega $
-block of reals.
$\alpha ^{th} \ \omega $
-block of reals. -
•
 to be a name for the collection of all Ord many
to be a name for the collection of all Ord many
 $\omega $
-blocks.
$\omega $
-blocks.
We claim that in the symmetric extension
,
![]() $A = \dot {A}^G$
is an amorphous proper class. To see why it is amorphous, suppose that
$A = \dot {A}^G$
is an amorphous proper class. To see why it is amorphous, suppose that
![]() $\dot {B}$
were a symmetric name such that for some
$\dot {B}$
were a symmetric name such that for some
![]() $p \in \mathbb {P}$
,
$p \in \mathbb {P}$
,
![]() $p \Vdash \dot {B} \subseteq \dot {A}$
. Take
$p \Vdash \dot {B} \subseteq \dot {A}$
. Take
to be a finite set such that
![]() ${\textrm {fix}}(E) \subseteq {\textrm {sym}}(\dot {B})$
and let
${\textrm {fix}}(E) \subseteq {\textrm {sym}}(\dot {B})$
and let
The following claim is a standard argument, for example see [Reference Drake and Singh2], and therefore we omit its proof.
Claim 7.12. For any
![]() $q \leq p$
, if there is an
$q \leq p$
, if there is an
![]() $\alpha \not \in y$
such that
$\alpha \not \in y$
such that
![]() $q \Vdash \dot {T}_\alpha \in \dot {B}$
, then
$q \Vdash \dot {T}_\alpha \in \dot {B}$
, then
![]() $q \Vdash \dot {T}_\beta \in \dot {B}$
for any
$q \Vdash \dot {T}_\beta \in \dot {B}$
for any
![]() $\beta \not \in y$
.
$\beta \not \in y$
.
Therefore, for any
![]() $q \leq p$
,
$q \leq p$
,
and so
![]() $\dot {A}$
will indeed be forced to be an amorphous class.
$\dot {A}$
will indeed be forced to be an amorphous class.
The second model is the system with
![]() , permutations given by
, permutations given by
![]() $\pi p (\pi \alpha , n) = p (\alpha , n)$
where
$\pi p (\pi \alpha , n) = p (\alpha , n)$
where
![]() $\pi $
is a permutation of Ord and
$\pi $
is a permutation of Ord and
![]() $\mathcal {F}$
is the filter generated by
$\mathcal {F}$
is the filter generated by
![]() ${\textrm {fix}}(E)$
for finite sets
${\textrm {fix}}(E)$
for finite sets
![]() . This system will add a Dedekind-finite class of Cohen reals, A, and it can be proven that if B is an infinite subclass of A then B is a proper class.
. This system will add a Dedekind-finite class of Cohen reals, A, and it can be proven that if B is an infinite subclass of A then B is a proper class.
The fact that both of these symmetric submodels fail to satisfy the Collection Scheme follows from the following slightly more general theorem.
Theorem 7.13. Suppose that
![]() satisfies;
satisfies;
-
1.
 ,
, -
2.
 and
and
 and
and -
3.

Then the Collection Scheme fails in
![]() . Moreover,
. Moreover,
![]() does not have a cumulative hierarchy and therefore Power Set also fails.
does not have a cumulative hierarchy and therefore Power Set also fails.
Proof. To prove that the Collection Scheme fails consider classes b satisfying
Since
![]() $\bigcup b \cap A$
is an infinite subclass of A, by the third assumption b must be a proper class. Therefore, while for every
$\bigcup b \cap A$
is an infinite subclass of A, by the third assumption b must be a proper class. Therefore, while for every
![]() $n \in \omega $
there is a y such that
$n \in \omega $
there is a y such that
![]() $(|y| = n \ \wedge \ y \subseteq A)$
there is no set witnessing this for all n.
$(|y| = n \ \wedge \ y \subseteq A)$
there is no set witnessing this for all n.
For the “moreover” part of the theorem, we shall in fact prove that any well-orderable sequence of sets can only contain finitely many elements of A. To see this, let
![]() be an indexed sequence of sets where I is either Ord or an infinite ordinal. We shall show that
be an indexed sequence of sets where I is either Ord or an infinite ordinal. We shall show that
![]() $\bigcup \mathcal {C} \cap A$
is finite and therefore that
$\bigcup \mathcal {C} \cap A$
is finite and therefore that
![]() $\mathcal {C}$
cannot be a hierarchy for the universe. Suppose for a contradiction that
$\mathcal {C}$
cannot be a hierarchy for the universe. Suppose for a contradiction that
![]() $\bigcup \mathcal {C} \cap A$
was in fact infinite. First note that for any
$\bigcup \mathcal {C} \cap A$
was in fact infinite. First note that for any
![]() ,
,
![]() $C_\alpha \cap A$
must be finite. Now we define a sequence of ordinals
$C_\alpha \cap A$
must be finite. Now we define a sequence of ordinals
![]() inductively as the least ordinal
inductively as the least ordinal
![]() such that
such that
![]() $(C_\alpha \setminus \bigcup _{m \in n} C_{\delta _m}) \cap A \neq \emptyset $
. Such an ordinal must exist by the assumption that
$(C_\alpha \setminus \bigcup _{m \in n} C_{\delta _m}) \cap A \neq \emptyset $
. Such an ordinal must exist by the assumption that
![]() $\bigcup \mathcal {C} \cap A$
is infinite and that
$\bigcup \mathcal {C} \cap A$
is infinite and that
![]() $\bigcup _{m \in n} (C_{\delta _m} \cap A)$
is a union of finite sets. But then
$\bigcup _{m \in n} (C_{\delta _m} \cap A)$
is a union of finite sets. But then
![]() $\bigcup _{n \in \omega } C_{\delta _n} \cap A$
is an infinite set, contradicting the third condition of the theorem.⊣
$\bigcup _{n \in \omega } C_{\delta _n} \cap A$
is an infinite set, contradicting the third condition of the theorem.⊣
Karagila [Reference Karagila16] claims that, over GB, any symmetric submodel of a tameFootnote
7
class forcing will again be a model of GB. However, since it is not necessarily true that the symmetric submodel of a pretame class forcing of a model of
![]() is again a model of
is again a model of
![]() we have the following three natural general questions:
we have the following three natural general questions:
Question 7.14.
-
• Suppose that
 . Let
. Let
 $\mathbb {P}$
be a pretame class forcing and
$\mathbb {P}$
be a pretame class forcing and
 $\langle \mathbb {P}, \mathcal {G}, \mathcal {F} \rangle $
a symmetric system with symmetric submodel N. What theory does N satisfy?
$\langle \mathbb {P}, \mathcal {G}, \mathcal {F} \rangle $
a symmetric system with symmetric submodel N. What theory does N satisfy? -
• Is there a combinatorial condition one can place on a symmetric system so that the symmetric submodel will satisfy
 ?
? -
• Which class versions of sets whose existence is incompatible with Choice can exist over models of GB or
 ?
?
In general, this final problem seems to be a difficult one to answer because, as shown by Monro in [Reference Monro20], it is consistent to have a Dedekind-finite proper class:
Theorem 7.15 (Monro).
Let ZF(K) be the theory with the language of ZF plus a one-place predicate K and let M be a countable transitive model of ZF. Then there is a model N such that N is a transitive model of ZF(K) and

In fact it is possible to have a class symmetric system which adds a Dedekind-finite class out of Ord many Cohen reals, is pretame and such that the symmetric submodel is a model of
![]() This is obtained as a symmetric submodel of the forcing
This is obtained as a symmetric submodel of the forcing
![]() which adds a block of
which adds a block of
![]() $\omega $
many Cohen reals for each ordinal. The permutation class is then those permutations which preserve the blocks and then permute within the block and the filter is, as usual, generated by the permutations which fix finite subsets of
$\omega $
many Cohen reals for each ordinal. The permutation class is then those permutations which preserve the blocks and then permute within the block and the filter is, as usual, generated by the permutations which fix finite subsets of
![]() .
.
The reason why the symmetric submodel in this case models both Collection and Separation is that for any pair
![]() there is some ordinal
there is some ordinal
![]() $\alpha $
such that for any permutation
$\alpha $
such that for any permutation
![]() $\pi $
,
$\pi $
,
![]() $\langle \pi \dot {y}, \pi p \rangle $
can be seen as an element of the set forcing
$\langle \pi \dot {y}, \pi p \rangle $
can be seen as an element of the set forcing
![]() ${\textrm {Add}}(\omega , \alpha \times \omega )$
. This means that for any H in the filter of subgroups,
${\textrm {Add}}(\omega , \alpha \times \omega )$
. This means that for any H in the filter of subgroups,
![]() $\{ \langle \pi \dot {y}, \pi p \rangle \colon \pi \in H \}$
is a set which is a sufficient condition to prove the Collection Scheme.
$\{ \langle \pi \dot {y}, \pi p \rangle \colon \pi \in H \}$
is a set which is a sufficient condition to prove the Collection Scheme.
To conclude this work we outline an approach to solving the first question from Question 7.14, which we will study further in future work. As before, suppose that
![]() $\mathbb {M}$
is a countable transitive model of
$\mathbb {M}$
is a countable transitive model of
![]() and that
and that
![]() $\langle \mathbb {P}, \mathcal {G}, \mathcal {F} \rangle $
is a symmetric system where
$\langle \mathbb {P}, \mathcal {G}, \mathcal {F} \rangle $
is a symmetric system where
![]() $\mathbb {P}$
is a pretame class forcing. We shall say that a class name
$\mathbb {P}$
is a pretame class forcing. We shall say that a class name
![]() $\dot {\Gamma }$
is
$\dot {\Gamma }$
is
![]() $\mathcal {F}$
-respected if
$\mathcal {F}$
-respected if
![]() and hereditarily
and hereditarily
![]() $\mathcal {F}$
-respected if this property holds hereditarily. Let HR be the class of names
$\mathcal {F}$
-respected if this property holds hereditarily. Let HR be the class of names
![]() which are hereditarily respected.
which are hereditarily respected.
The purpose of defining symmetric names in this way is to circumvent the issue that, for an arbitrary element H of the filter,
![]() $\{ \pi \dot {x} \colon \pi \in H \}$
may well be a proper class. However, in the set forcing case, the two resulting extensions are equal. That is to say, if
$\{ \pi \dot {x} \colon \pi \in H \}$
may well be a proper class. However, in the set forcing case, the two resulting extensions are equal. That is to say, if
![]() $\mathbb {P}$
is a set forcing and
$\mathbb {P}$
is a set forcing and
![]() $G \subseteq \mathbb {P}$
is generic then
$G \subseteq \mathbb {P}$
is generic then
![]() because any respected name is easily seen to be equivalent to a symmetric name by closing under its symmetry group.
because any respected name is easily seen to be equivalent to a symmetric name by closing under its symmetry group.
Now, suppose that our symmetric system is tenacious.Footnote
8
Let
![]() $\dot {f}$
be a name for a function,
$\dot {f}$
be a name for a function,
![]() $\dot {a}$
a name for its domain and
$\dot {a}$
a name for its domain and
![]() $\dot {b}$
the obvious class forcing name for
$\dot {b}$
the obvious class forcing name for
![]() $f"a$
, for example take the name defined in Theorem 3.1 of [Reference Holy, Krapf and Schlicht10]. Then, for an appropriately chosen
$f"a$
, for example take the name defined in Theorem 3.1 of [Reference Holy, Krapf and Schlicht10]. Then, for an appropriately chosen
![]() $q \in G$
and any
$q \in G$
and any
![]() $\pi $
fixing q,
$\pi $
fixing q,
![]() $\dot {a}$
and
$\dot {a}$
and
![]() $\dot {f}$
we will have that
$\dot {f}$
we will have that
![]() . Thus Replacement will hold in
. Thus Replacement will hold in
![]() . Moreover, one can show that
. Moreover, one can show that
![]() is a model of
is a model of
![]() . However, either of our earlier class symmetric systems will still witness the failure of the Collection Scheme in this model.
. However, either of our earlier class symmetric systems will still witness the failure of the Collection Scheme in this model.
Acknowledgements
This paper is part of the author’s Ph.D. thesis, supervised by Andrew Brooke-Taylor and Michael Rathjen, which was funded by an EPSRC Doctoral Training Grant. I am grateful to Philipp Schlicht for pointing out the use of Dependent Choice in the original proof of Corollary 6.8, Johannes Schürz whose suggestion of considering amorphous classes led to the second half of this paper and Asaf Karagila for many insightful conversations about symmetric submodels. I would also like to thank Bea Adam-Day and John Howe for sitting through and then giving feedback on various early iterations of this work.