No CrossRef data available.
Published online by Cambridge University Press: 12 March 2014
An analogue of a theorem of Sierpinski about the classical operation (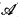 ) provides the motivation for studying κ-Suslin logic, an extension of Lκ+ω which is closed under a propositional connective based on (
) provides the motivation for studying κ-Suslin logic, an extension of Lκ+ω which is closed under a propositional connective based on (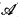 ). This theorem is used to obtain a complete axiomatization for κ-Suslin logic and an upper bound on the κ-Suslin accessible ordinals (for κ = ω these results are due to Ellentuck [E]). It also yields a weak completeness theorem which we use to generalize a result of Barwise and Kunen [B-K] and show that the least ordinal not H(κ+) recursive is the least ordinal not κ-Suslin accessible.
). This theorem is used to obtain a complete axiomatization for κ-Suslin logic and an upper bound on the κ-Suslin accessible ordinals (for κ = ω these results are due to Ellentuck [E]). It also yields a weak completeness theorem which we use to generalize a result of Barwise and Kunen [B-K] and show that the least ordinal not H(κ+) recursive is the least ordinal not κ-Suslin accessible.
We assume familiarity with lectures 3, 4 and 10 of Keisler's Model theory for infinitary logic [Ke]. We use standard notation and terminology including the following.
Lκ+ω is the logic closed under negation, finite quantification, and conjunction and disjunction over sets of formulas of cardinality at most κ. For κ singular, conjunctions and disjunctions over sets of cardinality κ can be replaced by conjunctions and disjunctions over sets of cardinality less than κ so that we can (and will in §2) assume the formation rules of Lκ+ω allow conjunctions and disjunctions only over sets of cardinality strictly less than κ whenever κ is singular.