Throughout this paper κ denotes an infinite cardinal, S = Sym(κ) and G is a subgroup of S. We shall be seeking the subgroups G with [S: G] < 2κ. In [2], the following result was proved.

Theorem 1. If [S: G] ≤ κthen there exists a subset Δ of k such that ∣Δ∣ < k and S(Δ) ≤ G.

Here S(Δ) = Sym(K/⊿) is the pointwise stabilizer of Δ in S.

However, the converse of Theorem 1 is not true. For if cf(κ) ≤ ∣Δ∣ < κ, then [S: S(Δ)] ≥ κcf(κ) > κ. This suggests that a substantially sharpened version of Theorem 1 may be true.

Question 1 [2]. Is it provable in ZFC, or even in ZFC with GCH, that if [S: G] ≤ κ then there is a subset Δ of κ such that ∣Δ∣ < cf(κ) and S(Δ) ≤ G?

At least two of the authors of [2] made a serious attempt to answer the above question positively. In §3, we shall see that they were essentially trying to prove that measurable cardinals do not exist.

The following result, due independently to Semmes [5] and Neumann [2], suggests a second way in which Theorem 1 might be improved.

Theorem 2. If k = ℵ0and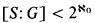then there is a finite subset Δ of k such thatS(Δ) ≤ G.

Question 2 [2]. Is it provable in ZFC that if [S: G] < 2κ then there is a subset Δ of κ such that ∣Δ∣ < κ and S(Δ) < G?

This question will be answered negatively in §4.