Nielsen [7] has proved that every subgroup of a free group of finite rank is free. The theorem was later strengthened by Schreier [8] by eliminating the finiteness restriction on the rank. Several proofs of this theorem (known as the Nielsen-Schreier theorem, henceforth denoted by NS) have appeared since Schreier's 1927 paper (see [1] and [2]). All proofs of NS use the axiom of choice (AC) and it is natural to ask whether NS is equivalent to AC. Läuchli has given a partial answer to this question by proving [6] that the negation of NS is consistent with ZFA (Zermelo-Fraenkel set theory weakened to permit the existence of atoms). By the Jech-Sochor embedding theorem (see [3] and [4]) ZFA can be replaced by ZF. Some form of AC, therefore, is needed to prove NS. The main purpose of this paper is to give a further answer to this question.

In §2 we prove that NS implies ACffin (the axiom of choice for sets of finite sets). In §3 we show that a strengthened version of NS implies AC and in §4 we give a partial list of open problems.

Let y be a set; ∣y∣ denotes the cardinal number of y and (y) is the power set of y. If p is a permutation of y and t ∈ y, the p-orbit of t is the set {pn(t): n is an integer}. If

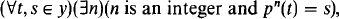
we call p a cyclic permutation of y. If f is a function with domain y and x ⊆ y, f″x denotes the set {f(t):t ∈ x}. If A is a subset of a group (G, °) (sometimes (G, °) will be denoted by G) then A−1= {x−1:x ∈ A} and [A] denotes the subgroup of G generated by A.