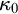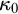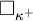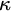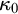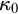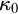1 Introduction and preliminaries
It is well-known (see [Reference Solovay, Reinhardt and Kanamori14, Corollary 4.9]) that if
$\kappa $
is a strongly compact cardinal, then
$\square _\lambda $
must fail for every
$\lambda \ge \kappa $
. Consequently, if
$\kappa $
is supercompact,
$\square _{\kappa ^+}$
must fail, so by reflection, there must be an unbounded subset
$A_0 \subseteq \kappa $
consisting of inaccessible cardinals on which
$\square _{\lambda ^+}$
fails for every
$\lambda \in A_0$
. Similarly, if
$\kappa $
is supercompact and
$2^\kappa = \kappa ^+$
, then again by reflection, there must be an unbounded subset
$A_1 \subseteq \kappa $
consisting of inaccessible cardinals such that for every
$\lambda \in A_1$
,
$2^\lambda = \lambda ^+$
. It is also the case (see [Reference Kanamori8, Propositions 26.11 and 26.12]) that if
$\kappa $
is supercompact, the
$\kappa $
must have a normal measure concentrating on Woodin cardinals, and hence cannot be the least Woodin cardinal.
The purpose of this paper is to show that the three properties of supercompact cardinals mentioned in the previous paragraph can consistently fail if
$\kappa $
is a non-supercompact strongly compact cardinal. In particular, we will prove the following theorems.
Theorem 1.1. Con(ZFC + There exists a supercompact cardinal)
$\Longrightarrow $
Con(ZFC + There is a non-supercompact strongly compact cardinal
$\kappa _0$
(the least measurable cardinal) and
$\square _{\kappa ^+}$
holds for every inaccessible cardinal
$\kappa \neq \kappa _0$
).
Theorem 1.2. Con(ZFC + There exists a supercompact cardinal)
$\Longrightarrow $
Con(ZFC + There is a non-supercompact strongly compact cardinal
$\kappa _0$
(the least measurable cardinal) such that
$2^{\kappa _0} = \kappa ^+_0$
yet
$2^\kappa = \kappa ^{++}$
for every inaccessible cardinal
$\kappa \neq \kappa _0$
).
Theorem 1.3. Con(ZFC + There exists a strongly compact cardinal with a Woodin cardinal above it)
$\Longrightarrow $
Con(ZFC + The least strongly compact cardinal is less than the least Woodin cardinal).
We take this opportunity to make a few remarks concerning Theorems 1.1–1.3. Because of [Reference Solovay, Reinhardt and Kanamori14, Corollary 4.9], the model witnessing the conclusions of Theorem 1.1 will have no inaccessible cardinals above
$\kappa _0$
. On the other hand, as our proof will show, there can be models satisfying the conclusions of Theorem 1.2 containing a proper class of inaccessible cardinals, as long as no cardinal
$\lambda> \kappa _0$
is measurable. Further, as the referee has pointed out, in any model witnessing the conclusions of either Theorem 1.1 or 1.2, if
$j : V \to M$
is an arbitrary
$\lambda $
-strong compactness embedding for
$\lambda \ge \kappa _0$
, then it must be the case that
$(\kappa ^{++}_0)^M < (\kappa ^{++}_0)^V$
. In addition, depending on the exact nature of the ground model, the large cardinal structure of the model witnessing the conclusion of Theorem 1.3 can essentially be arbitrary. Also, Theorem 1.3 provides a specific instance illustrating some general phenomena about the possible relationships between the least strongly compact cardinal and other members of the large cardinal hierarchy. The issues mentioned in the preceding two sentences will be discussed at greater length immediately following the proof of Theorem 1.3.
Before beginning the proofs of Theorems 1.1–1.3, we give some preliminary information. When forcing,
$q \ge p$
means that q is stronger than p. For
$\kappa $
a regular cardinal and
$\lambda $
an ordinal,
$\mathrm {Add}(\kappa , \lambda )$
is the standard partial ordering for adding
$\lambda $
many Cohen subsets of
$\kappa $
. For
$\alpha < \beta $
ordinals,
$[\alpha , \beta ]$
,
$[\alpha , \beta )$
,
$(\alpha , \beta ]$
, and
$(\alpha , \beta )$
are as in standard interval notation. If G is
${\mathbb P}$
-generic over V, we will abuse notation slightly and use both
$V[G]$
and
$V^{\mathbb P}$
to indicate the universe obtained by forcing with
${\mathbb P}$
. We will, from time to time, confuse terms with the sets they denote and write x when we actually mean
$\dot x$
or
$\check x$
.
The partial ordering
${\mathbb P}$
is
$\kappa $
-strategically closed if in the two person game in which the players construct an increasing sequence
$\langle p_\alpha : \alpha \le \kappa \rangle $
, where player I plays odd stages and player II plays even stages (choosing the trivial condition at stage 0), player II has a strategy which ensures the game can always be continued. Note that if
${\mathbb P}$
is
$\kappa $
-strategically closed and
$f : \kappa \to V$
is a function in
$V^{\mathbb P}$
, then
$f \in V$
.
A corollary of Hamkins’ work on gap forcing found in [Reference Hamkins5, Reference Hamkins6] will be employed in the proofs of Theorems 1.1–1.3. We therefore state as a separate theorem what is relevant for this paper, along with some associated terminology, quoting from [Reference Hamkins5, Reference Hamkins6] when appropriate. Suppose
${\mathbb P}$
is a partial ordering which can be written as
${\mathbb Q} \ast \dot {\mathbb R}$
, where
${\vert {\mathbb Q} \vert } < \delta $
,
${\mathbb Q}$
is nontrivial, and
$\Vdash _{\mathbb Q} "\dot {\mathbb R}$
is
$\delta $
-strategically closed.” In Hamkins’ terminology of [Reference Hamkins5, Reference Hamkins6],
${\mathbb P}$
admits a gap at
$\delta $
. Also, as in the terminology of [Reference Hamkins5, Reference Hamkins6], and elsewhere, an embedding
$j : \overline V \to \overline M$
is amenable to
$\overline V$
when
$j \restriction A \in \overline V$
for any
$A \in \overline V$
. The specific corollary of Hamkins’ work from [Reference Hamkins5, Reference Hamkins6] we will be using is then the following.
Theorem 1.4 (Hamkins)
Suppose that
$V[G]$
is a generic extension obtained by forcing that admits a gap at some regular
$\delta < \kappa $
. Suppose further that
$j: V[G] \to M[j(G)]$
is an embedding with critical point
$\kappa $
for which
$M[j(G)] \subseteq V[G]$
and
${M[j(G)]}^\delta \subseteq M[j(G)]$
in
$V[G]$
. Then
$M \subseteq V$
; indeed,
$M = V \cap M[j(G)]$
. If the full embedding j is amenable to
$V[G]$
, then the restricted embedding
$j \restriction V : V \to M$
is amenable to V. If j is definable from parameters (such as a measure or extender) in
$V[G]$
, then the restricted embedding
$j \restriction V$
is definable from the names of those parameters in V.
It immediately follows from Theorem 1.4 that after forcing with a measurable cardinal preserving partial ordering admitting a gap at a small regular cardinal such as
$\omega $
, the measurable cardinals in both the ground model and generic extension are exactly the same.
Recall that if
$\kappa $
is an arbitrary uncountable cardinal,
$\square _\kappa $
is the principle stating that there exists a sequence of sets
$\langle C_\alpha \mid \alpha < \kappa ^+$
and
$\alpha $
is a limit ordinal
$\rangle $
such that
$C_\alpha $
is a closed, unbounded subset of
$\alpha $
so that if
$\mathrm {cf}(\alpha ) < \kappa $
, then
$\mathrm {ot}(C_\alpha ) < \kappa $
, with the additional coherence property that for any limit point
$\beta \in C_\alpha $
,
$C_\alpha \cap \beta = C_\beta $
. For basic facts about
$\square _\kappa $
, readers are urged to consult [Reference Cummings, Foreman and Magidor4, Section 2]. We do note that
$\square _\kappa $
is preserved in any outer model of V containing the same
$\kappa ^+$
. This is since the notions of being closed, unbounded and the square sequence being coherent are both
$\Delta _0$
and hence are upwards absolute.
Finally, in the proof of Lemma 2.2, we will mention the “standard lifting techniques” for lifting a
$\lambda $
-supercompactness embedding
$j : V \to M$
generated by a supercompact ultrafilter over
$P_\kappa (\lambda )$
to a generic extension given by a suitably defined Easton support iteration. Very briefly, we assume the following, where for the remainder of the exposition, for any cardinal
$\kappa $
,
$\kappa ^*$
is the least inaccessible cardinal above
$\kappa $
:
-
1.
$V \vDash \mathrm {GCH}$
. -
2.
$\lambda \ge \kappa $
is a regular cardinal. -
3.
${\mathbb P} = \langle \langle {\mathbb P}_\delta , \dot {\mathbb Q}_\delta \rangle \mid \delta < \kappa \rangle $
is an Easton support iteration having length
$\kappa $
. -
4. The only nontrivial stages of forcing (possibly) occur at inaccessible cardinals.
-
5. G is
${\mathbb P}$
-generic over V. -
6. For any inaccessible cardinal
$\delta < \kappa $
,
$\Vdash _{{\mathbb P}_\delta } "{\vert \dot {\mathbb Q}_\delta \vert } < \check \delta ^*$
.”Footnote
1
-
7.
$j({\mathbb P}) = {\mathbb P} \ast \dot {\mathbb Q} = {\mathbb P}_\kappa \ast \dot {\mathbb Q}$
and in M,
$\Vdash _{{\mathbb P}_\kappa } "\dot {\mathbb Q}$
is (at least)
$\lambda ^+$
-strategically closed.”
When
$\lambda = \kappa $
, since a supercompact ultrafilter over
$P_\kappa (\kappa )$
is essentially the same thing as a normal measure over
$\kappa $
, we assume without loss of generality that the embedding j is generated by a normal measure over
$\kappa $
.
Since
$V \vDash \mathrm {GCH}$
,
$M[G]\vDash "{\vert {\mathbb Q} \vert } = j(\kappa )$
,” and
$V \vDash "{\vert j(\kappa ^+) \vert } = {\vert j(2^\kappa ) \vert } = \vert \{f \mid f : $
$P_\kappa (\lambda ) \to \kappa ^+\} \vert = {\vert \{f \mid f : \lambda \to \kappa ^+\} \vert } = {\vert \{f \mid f : \lambda \to \lambda \} \vert } $
,”
$V[G] \vDash "$
There are
$\lambda ^+ = 2^\lambda = {\vert j(\kappa ^+) \vert } = {\vert j(2^\kappa ) \vert } $
many dense open subsets of
${\mathbb Q}$
present in
$M[G]$
.” Because
${\mathbb P}$
is
$\kappa $
-c.c. and
$\lambda \ge \kappa $
,
$M[G]$
remains
$\lambda $
-closed with respect to
$V[G]$
. As
${\mathbb Q}$
is therefore
$\lambda ^+$
-strategically closed in both
$M[G]$
and
$V[G]$
, working in
$V[G]$
, it is possible to build a
${\mathbb Q}$
-generic object H over
$M[G]$
such that
$j " G \subseteq G \ast H$
. The construction of H is analogous to the construction of the generic object
$G_1$
found in [Reference Apter and Cummings3, Lemma 4]. Still working in
$V[G]$
, one then lifts j to
$j : V[G] \to M[G][H]$
witnessing the
$\lambda $
-supercompactness of
$\kappa $
in
$V[G]$
.
2 The proofs of Theorems 1.1–1.3
We turn now to the proofs of our theorems, beginning with the proof of Theorem 1.1.
Proof Suppose
$V \vDash "$
ZFC +
$\kappa _0$
is supercompact.” Without loss of generality, by first doing a preliminary forcing and then truncating the universe if necessary, we assume in addition that
$V \vDash "$
GCH + No cardinal
$\kappa $
is supercompact up to
$\kappa ^*$
” (where
$\kappa $
is supercompact up to
$\lambda $
if
$\kappa $
is
$\gamma $
-supercompact for every
$\gamma < \lambda $
). In particular, this immediately implies that
$V \vDash "$
No cardinal
$\lambda> \kappa _0$
is inaccessible,” a fact which remains true in any generic extension of V as well.
We are now in a position to define the first partial ordering
${\mathbb P}^0$
used in the proof of Theorem 1.1.
${\mathbb P}^0 = \langle \langle {\mathbb P}^0_\delta , \dot {\mathbb Q}^0_\delta \rangle \mid \delta < \kappa _0 \rangle $
is the Easton support iteration of length
$\kappa _0$
which begins by adding a Cohen subset of
$\omega $
, i.e.,
${\mathbb P}^0_0$
is the trivial partial ordering
$\{\emptyset \}$
, and
$\dot {\mathbb Q}^0_0 = \check {\mathrm {Add}}(\omega , 1)$
. This ensures a gap at
$\omega $
. At all other stages
$\delta> 0$
,
$\dot {\mathbb Q}^0_\delta = \{\check \emptyset \}$
, except if
$\delta < \kappa _0$
is a non-measurable inaccessible cardinal in V. Under these circumstances,
$\dot {\mathbb Q}^0_\delta $
is a term for the partial ordering
${\mathbb P}(\delta ^+)$
of [Reference Apter1, Section 0] which adds a
$\square _{\delta ^+}$
sequence.Footnote
2
Standard arguments show that
$V^{{\mathbb P}^0} \vDash $
GCH and that V and
$V^{{\mathbb P}^0}$
have the same cardinals and cofinalities.
Lemma 2.1.
$V^{{\mathbb P}^0} \vDash "$
For every
$\kappa < \kappa _0$
which is in V a non-measurable inaccessible cardinal,
$\square _{\kappa ^+}$
holds.”
Proof Suppose
$\kappa < \kappa _0$
is a non-measurable inaccessible cardinal in V. Write
${\mathbb P}^0 = {\mathbb P}_{\kappa + 1}^0 \ast \dot {\mathbb P}^{0, \kappa + 1}$
. By the definition of
${\mathbb P}^0$
,
$V^{{\mathbb P}_{\kappa + 1}^0} \vDash "\square _{\kappa ^+}$
holds.” Since by the definition of
${\mathbb P}^0$
,
$\Vdash _{{\mathbb P}_{\kappa + 1}^0} "\dot {\mathbb P}^{0, \kappa + 1}$
is
$(\kappa ^*)^+$
-strategically closed,”
$V^{{\mathbb P}_{\kappa + 1}^0 \ast \dot {\mathbb P}^{0, \kappa + 1}} = V^{{\mathbb P}^0} \vDash "\square _{\kappa ^+}$
holds.” This completes the proof of Lemma 2.1.
Lemma 2.2. If
$V \vDash "\kappa \le \lambda $
are such that
$\kappa $
is
$\lambda $
-supercompact and
$\lambda $
is regular,” then
$V^{{\mathbb P}^0} \vDash "\kappa $
is
$\lambda $
-supercompact.”
Proof Let
$\kappa \le \lambda $
be as in the hypotheses of Lemma 2.2, with
$j : V \to M$
an elementary embedding witnessing the
$\lambda $
-supercompactness of
$\kappa $
generated by a supercompact ultrafilter over
$P_\kappa (\lambda )$
. Because
$V \vDash "$
No cardinal above
$\kappa _0$
is inaccessible,” it follows that
$\kappa \le \kappa _0$
. Write
${\mathbb P}^0 = {\mathbb P}^0_\kappa \ast \dot {\mathbb P}^{0, \kappa }$
.Footnote
3
Since
$V \vDash "\kappa $
isn’t supercompact up to
$\kappa ^*$
,”
$\lambda \in (\kappa , \kappa ^*)$
. In addition, because
$V \vDash "\kappa $
is measurable,” only trivial forcing is done at any stage
$\delta \in [\kappa , \kappa ^*)$
in the definition of
${\mathbb P}^0$
. It follows that
$\Vdash _{{\mathbb P}^0_\kappa } "\dot {\mathbb P}^{0, \kappa }$
is
$(\kappa ^*)^+$
-strategically closed,” so to complete the proof of Lemma 2.2, it suffices to show
$V^{{\mathbb P}^0_\kappa } \vDash "\kappa $
is
$\lambda $
-supercompact.”
To do this, we consider two cases.
Case 1:
$\kappa < \lambda $
. By GCH and the fact that
$\lambda \ge \kappa ^+ = 2^\kappa $
,
$M \vDash "\kappa $
is measurable.” This means that in M,
$\kappa $
is a trivial stage of forcing. By the definition of
${\mathbb P}^0$
, we may therefore write
$j({\mathbb P}^0_\kappa ) = {\mathbb P}^0_\kappa \ast \dot {\mathbb Q}$
, where the first nontrivial stage forced to occur in
$\dot {\mathbb Q}$
in M is well above
$\lambda $
. In particular,
$\kappa $
is forced to be a trivial stage in
$\dot {\mathbb Q}$
. Because this first nontrivial stage of forcing in M is at
$(\lambda ^*)^M = (\kappa ^*)^M$
, by the calculations given in the last paragraph of Section 1,
$\dot {\mathbb Q}$
is forced to be a
$\lambda ^+$
-strategically closed partial ordering whose power set has size
$(\lambda ^+)^V = (\lambda ^+)^{V[G]}$
. Consequently, the standard lifting techniques mentioned in the last paragraph of Section 1 then show that
$V^{{\mathbb P}^0_\kappa } \vDash "\kappa $
is
$\lambda $
-supercompact.”
Case 2:
$\kappa = \lambda $
. In this case, we only know that
$V \vDash "\kappa $
is
$\kappa $
-supercompact,” i.e.,
$V \vDash "\kappa $
is measurable.” Hence, by [Reference Kanamori8, Proposition 5.16], we may assume that
$j : V \to M$
is generated by a normal measure over
$\kappa $
of Mitchell order
$0$
, i.e., a normal measure over
$\kappa $
such that
$M \vDash "\kappa $
isn’t measurable.” We also have as before that
$j({\mathbb P}^0_\kappa ) = {\mathbb P}^0_\kappa \ast \dot {\mathbb Q}$
. It thus follows that
$\kappa $
is in M a nontrivial stage of forcing in
$\dot {\mathbb Q}$
. In particular,
$\dot {\mathbb Q}_\kappa $
is a term for the partial ordering adding a
$\square _{\kappa ^+}$
sequence. However, since
$M^\kappa \subseteq M$
and in M,
$\Vdash _{{\mathbb P}^0_\kappa } "\dot {\mathbb Q}_\kappa $
and thus
$\dot {\mathbb Q}$
are
$\kappa ^+$
-strategically closed,” the arguments of Case 1 remain valid and allow us to infer that
$V^{{\mathbb P}^0_\kappa } \vDash "\kappa $
is measurable.”
Cases 1 and 2 complete the proof of Lemma 2.2.
Since in Lemma 2.2,
$\lambda $
is an arbitrary regular cardinal, it immediately follows that
$V^{{\mathbb P}^0} \vDash "\kappa _0$
is supercompact.”
Lemma 2.3. The measurable cardinals in V and
$V^{{\mathbb P}^0}$
are exactly the same.
Proof As was mentioned in its definition,
${\mathbb P}^0$
admits a gap at
$\omega $
. By Lemma 2.2, all measurable cardinals in V are preserved when forcing with
${\mathbb P}^0$
. Therefore, by our remarks immediately following Theorem 1.4, the measurable cardinals in V and
$V^{{\mathbb P}^0}$
are exactly the same. This completes the proof of Lemma 2.3.
Let
$V_0 = V^{{\mathbb P}^0}$
. To complete the proof of Theorem 1.1, let
${\mathbb P}^1 \in V_0$
be the Magidor iteration of Prikry forcing from [Reference Magidor10] which changes the cofinality of every measurable cardinal
$\kappa < \kappa _0$
to
$\omega $
. Let
$V_1 = V^{{\mathbb P}^1}_0$
. Because
$V_0 \vDash "\kappa _0$
is strongly compact (as it is supercompact),” by the work of [Reference Magidor10],
$V_1 \vDash "\kappa _0$
is both strongly compact and the least measurable cardinal and so is not
$2^{\kappa _0} = \kappa ^+_0$
supercompact.” Since by Lemma 2.3, V and
$V_0$
contain the same measurable cardinals, the V-measurable cardinals
$\kappa < \kappa _0$
are the ones whose cofinality becomes
$\omega $
in
$V_1$
. This means that the inaccessible cardinals
$\kappa < \kappa _0$
in
$V_1$
were non-measurable inaccessible cardinals in both
$V_0$
and V. By Lemma 2.1,
$\square _{\kappa ^+}$
holds in
$V_0$
for every
$\kappa < \kappa _0$
which is inaccessible but non-measurable in V. Therefore, because there are no inaccessible cardinals above
$\kappa _0$
in
$V_1$
, forcing with
${\mathbb P}^1$
preserves cardinals, and for any uncountable cardinal
$\kappa $
,
$\square _\kappa $
is upwards absolute to any outer model of
$V_0$
containing the same
$\kappa ^+$
, we may now infer that
$V_1 \vDash "$
For every non-measurable inaccessible cardinal
$\kappa $
,
$\square _{\kappa ^+}$
holds.” This last fact, Lemmas 2.1–2.3, and the intervening comments complete the proof of Theorem 1.1.
We note that the proof of Theorem 1.1 can be modified so that, e.g.,
$\square _\lambda $
holds whenever
$\lambda \in (\kappa , \kappa ^{+ \aleph _{75}}]$
and
$\kappa \neq \kappa _0$
is inaccessible. We leave the proof of this and other, similar modifications to the readers of this paper. What is not possible, however, is to construct a model with a strongly compact cardinal
$\kappa _0$
(supercompact or otherwise) in which
$\square _\kappa $
holds for every inaccessible cardinal
$\kappa \neq \kappa _0$
. In order to see this, we consider first the following fact.
Proposition 2.4. Suppose
$\kappa $
is a measurable cardinal and
$\square _\lambda $
holds for every inaccessible cardinal
$\lambda < \kappa $
. Then
$\square _\kappa $
holds as well.
Assuming Proposition 2.4, the impossibility of the
$\kappa ^+$
-strong compactness of some cardinal
$\kappa $
together with
$\square _\lambda $
holding for every inaccessible cardinal
$\lambda < \kappa $
follows easily. This is since, as mentioned in our opening remarks, if
$\kappa $
is
$\kappa ^+$
-strongly compact, then
$\square _{\kappa }$
must fail.
Proof To prove Proposition 2.4, let
$j : V \to M$
be an elementary embedding witnessing the measurability of
$\kappa $
generated by a normal measure over
$\kappa $
. If
$V \vDash "$
For every inaccessible
$\lambda < \kappa $
,
$\square _\lambda $
holds,” then by elementarity,
$M \vDash "$
For every inaccessible
$\lambda < j(\kappa )$
,
$\square _\lambda $
holds.” Because
$j(\kappa )> \kappa $
and
$M^\kappa \subseteq M$
, we may consequently infer that
$M \vDash "\kappa $
is inaccessible and
$\square _\kappa $
holds.” As
$M \subseteq V$
,
$M^\kappa \subseteq M$
, and
$(\kappa ^+)^M = (\kappa ^+)^V$
, any
$\square _\kappa $
sequence in M is also a
$\square _\kappa $
sequence in V, i.e.,
$V \vDash "\square _\kappa $
holds.” This completes the proof of Proposition 2.4.
Although it is impossible for
$\kappa $
to be strongly compact and for
$\square _\kappa $
to hold, it is possible for
$\square _\kappa $
to be true when
$\kappa $
is a measurable cardinal. For example, in a canonical extender model
$L[\vec E]$
, a theorem of Schimmerling and Zeman [Reference Schimmerling and Zeman12, Theorem 2] tells us that
$\square _\kappa $
holds for every uncountable cardinal
$\kappa $
. Thus,
$\square _\kappa $
will be true whenever
$L[\vec E] \vDash "\kappa $
is a measurable cardinal.” In addition, as the referee has pointed out, since the standard partial ordering
${\mathbb P}(\kappa )$
for introducing a
$\square _\kappa $
sequence is
$\kappa $
-strategically closed and therefore adds no new subsets of
$\kappa $
,
$\kappa $
remains a measurable cardinal after forcing with
${\mathbb P}(\kappa )$
.
Having completed the proof of Theorem 1.1 and the subsequent discussion, we turn now to the proof of Theorem 1.2.
Proof Suppose
$V \vDash "$
ZFC +
$\kappa _0$
is supercompact.” In analogy to the proof of Theorem 1.1, by first doing a preliminary forcing and then truncating the universe if necessary, we assume in addition that
$V \vDash "$
GCH + No cardinal
$\kappa $
is supercompact up to a measurable cardinal.” In particular, this immediately implies that
$V \vDash "$
No cardinal
$\lambda> \kappa _0$
is measurable.” We do, however, explicitly note that unlike with Theorem 1.1, our assumptions allow for the existence of a (possibly proper) class of inaccessible cardinals above
$\kappa _0$
.
We are now in a position to define the first partial ordering
${\mathbb P}^0$
used in the proof of Theorem 1.2. First, let
$A = \{\delta \mid \delta $
is an inaccessible cardinal
$\}$
. We then define
$$ \begin{align*}\Omega = \begin{cases} \sup(A), & \text{if ot}(A)\ \text{is a limit ordinal,} \\ \max(A) + 1, & \text{if ot}(A)\ \text{is a successor ordinal,} \\ \rm{Ord}, & \text{if}\ A\ \text{is a proper class.} \end{cases}\end{align*} $$
${\mathbb P}^0 = \langle \langle {\mathbb P}^0_\delta , \dot {\mathbb Q}^0_\delta \rangle \mid \delta < \Omega \rangle $
is the Easton support iteration of length
$\Omega $
which begins by adding a Cohen subset of
$\omega $
, i.e., as in the proof of Theorem 1.1,
${\mathbb P}^0_0 = \{\emptyset \}$
and
$\dot {\mathbb Q}^0_0 = \check {\mathrm {Add}}(\omega , 1)$
. This again ensures a gap at
$\omega $
. At all other stages
$\delta> 0$
,
$\dot {\mathbb Q}^0_\delta = \{\check \emptyset \}$
, except if
$\delta < \kappa _0$
is an inaccessible cardinal in V. Under these circumstances,
$\dot {\mathbb Q}^0_\delta = \dot {\mathrm {Add}}(\delta , \delta ^{++})$
if
$\delta $
isn’t measurable in V, but
$\dot {\mathbb Q}^0_\delta = \dot {\mathrm {Add}}(\delta , \delta ^+)$
if
$\delta $
is measurable in V.
${\mathbb P}^0$
as just defined is the partial ordering used in the proof of [Reference Apter2, Theorem 4]. Therefore, the remarks immediately following Theorem 1.4 of this paper, in conjunction with the arguments found on [Reference Apter2, pp. 438–441] (with a particular reference made to the proofs of [Reference Apter2, Lemmas 3.4 and 3.5]), show that
$V^{{\mathbb P}^0} \vDash "$
ZFC +
$\kappa _0$
is supercompact + No cardinal
$\lambda> \kappa _0$
is measurable +
$2^\kappa = \kappa ^{++}$
if
$\kappa $
is a non-measurable inaccessible cardinal +
$2^\kappa = \kappa ^+$
if
$\kappa $
is a measurable cardinal.” In particular,
$V^{{\mathbb P}^0} \vDash "2^{\kappa _0} = \kappa ^+_0$
.”
Now, as in the proof of Theorem 1.1, let
$V_0 = V^{{\mathbb P}^0}$
, and also let once again
${\mathbb P}^1 \in V_0$
be the Magidor iteration of Prikry forcing from [Reference Magidor10] which changes the cofinality of every measurable cardinal
$\kappa < \kappa _0$
to
$\omega $
. As before,
$V_1 = V^{{\mathbb P}^1}_0 \vDash "\kappa _0$
is both strongly compact and the least measurable cardinal and so is not
$2^{\kappa _0} = \kappa ^+_0$
supercompact.” Since
$V_0 \vDash "{\vert {\mathbb P}^1 \vert } = 2^{\kappa _0} = \kappa ^+_0$
,” the Lévy–Solovay results [Reference Lévy and Solovay9] in conjunction with standard arguments yield that
$V_1 \vDash "$
No cardinal
$\lambda> \kappa _0$
is measurable + If
$\lambda> \kappa _0$
is inaccessible, then
$2^\lambda = \lambda ^{++}$
.” It follows that
$V_1 \vDash "\kappa _0$
is the only measurable cardinal.” By the definition of
${\mathbb P}^1$
, any inaccessible cardinal
$\kappa < \kappa _0$
in
$V_1$
was a non-measurable inaccessible cardinal in
$V_0$
. Consequently, since the argument found in [Reference Magidor10, last paragraph of Lemma 4.4] shows that forcing with
${\mathbb P}^1$
doesn’t change the cardinality of power sets of cardinals at or below
$\kappa _0$
,
$V_1 \vDash "2^{\kappa _0} = \kappa ^+_0$
yet
$2^\kappa = \kappa ^{++}$
for every inaccessible cardinal
$\kappa \neq \kappa _0$
.” This completes the proof of Theorem 1.2.
We remark that starting from a model containing a supercompact cardinal
$\kappa _0$
with no inaccessible cardinals above it, it is possible to combine the results of Theorems 1.1 and 1.2 to obtain a model in which
$\kappa _0$
is both the least strongly compact cardinal and the least measurable cardinal,
$\square _{\kappa ^+}$
holds for every inaccessible cardinal
$\kappa \neq \kappa _0$
, and
$2^{\kappa _0} = \kappa ^+_0$
yet
$2^\kappa = \kappa ^{++}$
for every inaccessible cardinal
$\kappa \neq \kappa _0$
. The proof proceeds by forcing first with the partial ordering
${\mathbb P}^0$
used in Theorem 1.1, then forcing next with the partial ordering
${\mathbb P}^0$
as defined in Theorem 1.2, and then finally forcing with the partial ordering
${\mathbb P}^1$
as defined in both Theorems 1.1 and 1.2. We leave it to the readers of this paper to fill in the missing details.
Having completed the proof of Theorem 1.2 and the subsequent discussion, we turn now to the proof of Theorem 1.3.
Proof Suppose
$V \vDash "$
ZFC +
$\kappa _0 < \kappa _1$
are such that
$\kappa _0$
is strongly compact and
$\kappa _1$
is the least Woodin cardinal above
$\kappa _0$
.” Let
${\mathbb P}$
once again be the Magidor iteration of Prikry forcing from [Reference Magidor10] which changes the cofinality of every measurable cardinal
$\kappa < \kappa _0$
to
$\omega $
, with
$V_0 = V^{\mathbb P}$
. Because
$V_0 \vDash "\kappa _0$
is both the least measurable and least strongly compact cardinal,” and because by [Reference Kanamori8, Exercise 26.10], any Woodin cardinal must be a limit of measurable cardinals,
$V_0 \vDash "$
No cardinal
$\kappa \le \kappa _0$
is a Woodin cardinal.” Since
$V \vDash "{\vert {\mathbb P} \vert } = 2^{\kappa _0}$
,” the arguments of [Reference Hamkins and Woodin7] (see also [Reference Hamkins6, Corollary 15] and [Reference Hamkins5, Corollary 6]) show that
$V_0 \vDash "\kappa _1$
is the least Woodin cardinal above
$\kappa _0$
.” From the preceding two sentences, we may now immediately infer that
$V_0 \vDash "\kappa _1$
is the least Woodin cardinal.” Thus, in
$V_0$
, the least strongly compact cardinal
$\kappa _0$
is less than the least Woodin cardinal
$\kappa _1$
. This completes the proof of Theorem 1.3.
We now take this opportunity to make a few observations concerning Theorem 1.3 and its proof. First, we remark that unlike Theorems 1.1 and 1.2, there are no restrictions placed on the large cardinal structure of either the ground model used in the proof of Theorem 1.3 or the generic extension witnessing the conclusions of Theorem 1.3. To see this, suppose that, e.g., we start with a ground model V containing a proper class of supercompact cardinals. Let
$\kappa _0 \in V$
be the least strongly compact cardinal (which might also be the least supercompact cardinal, as was first shown in [Reference Magidor10]). If we now force over V using the partial ordering
${\mathbb P}$
of Theorem 1.3 and once again let
$V_0 = V^{\mathbb P}$
, then by the results of [Reference Lévy and Solovay9], there will still be a proper class of supercompact cardinals in
$V_0$
. Since by [Reference Kanamori8, Propositions 26.11 and 26.12], any supercompact cardinal has a normal measure concentrating on Woodin cardinals, in
$V_0$
, let
$\kappa _1> \kappa _0$
be the least Woodin cardinal above
$\kappa _0$
(which, by the proof of Theorem 1.3, is the least Woodin cardinal in
$V_0$
). We have thus constructed a model containing a proper class of supercompact cardinals in which the least strongly compact cardinal is less than the least Woodin cardinal. Other models witnessing the conclusions of Theorem 1.3 using the arguments of this paragraph are also possible.
We note also that, as the referee has pointed out, there is nothing special about the notion of Woodin cardinal in Theorem 1.3. The work of [Reference Hamkins and Woodin7] and the arguments used in the proof of Theorem 1.3 show that it is consistent, relative to the existence of a strongly compact cardinal with a strong cardinal above it, for the least strongly compact cardinal to be less than the least strong cardinal. In fact, the proof of Theorem 1.3 actually shows the following metatheorem.
Theorem 2.5. Suppose that
$\varphi (x)$
is a formula in the language of ZF such that
$:$
-
1. For any ordinal
$\lambda $
,
$\varphi (\lambda )$
implies
$\lambda $
is a limit of measurable cardinals. -
2. If
$\varphi (\lambda )$
holds and
${\vert {\mathbb P} \vert } < \lambda $
, then forcing with
${\mathbb P}$
preserves
$\varphi (\lambda )$
and creates no new
$\kappa $
satisfying
$\varphi (\kappa )$
for any
$\kappa \ge {\vert {\mathbb P} \vert } $
.
It is then consistent, relative to the existence of a strongly compact cardinal with a cardinal
$\lambda $
above it satisfying
$\varphi (\lambda )$
, for the least strongly compact cardinal to be less than the least cardinal
$\lambda _0$
satisfying
$\varphi (\lambda _0)$
.
It is interesting to observe, though, that in spite of the fact that it is relatively consistent for the least strongly compact cardinal to be smaller than either the least Woodin cardinal or the least strong cardinal, the consistency strength of a cardinal
$\kappa $
such that
$\kappa $
is
$\kappa ^+$
-strongly compact far exceeds the consistency strength of either a strong cardinal or a Woodin cardinal. In particular, [Reference Schimmerling11, Theorem 5.16] shows that relative to the existence of a cardinal
$\kappa $
which is
$\kappa ^+$
-strongly compact, there is a model of height
$\kappa $
containing both a proper class of strong cardinals and a proper class of Woodin cardinals.
3 Concluding remarks
In conclusion to this paper, we pose the following open questions:
-
1. Is it possible to construct models in which
$\square _\kappa $
holds below the least strongly compact cardinal at every uncountable non-inaccessible cardinal
$\kappa $
? -
2. Is it possible to obtain models with more than one strongly compact cardinal below the least Woodin cardinal?
-
3. Is it possible to construct a model in which GCH fails everywhere below the least strongly compact cardinal
$\kappa _0$
? -
4. Is it possible to construct a model in which, for
$n \in \omega $
, the first n strongly compact cardinals
$\kappa _1, \ldots , \kappa _n$
are the first n measurable cardinals,
$2^{\kappa _i} = \kappa ^+_i$
for
$i = 1, \ldots , n$
, yet
$2^\kappa = \kappa ^{++}$
for every other inaccessible cardinal
$\kappa $
? -
5. In general, is it possible to construct a model with more than one non-supercompact strongly compact cardinal in which
$2^\kappa = \kappa ^+$
if
$\kappa $
is a non-supercompact strongly compact cardinal, yet
$2^\kappa = \kappa ^{++}$
for every other inaccessible cardinal
$\kappa $
?
Note that the answer to Question 3 is no, if
$\kappa _0$
is supercompact. This is since by Solovay’s theorem [Reference Solovay13] that GCH must hold at any singular strong limit cardinal above a strongly compact cardinal and the reflection properties of supercompact cardinals, below any supercompact cardinal, there must be many instances of GCH holding. Question 3 should be contrasted with Woodin’s question (see [Reference Kanamori8, Question 22.22]) of whether GCH holding below a strongly compact cardinal implies GCH holds everywhere. Regarding Question 4, it is a theorem of Magidor (unpublished by him, but appearing in a generalized form as [Reference Apter and Cummings3, Theorem 1]) that it is consistent, relative to
$n \in \omega $
supercompact cardinals, for the first n strongly compact cardinals to be the first n measurable cardinals. The proof methods used in [Reference Apter and Cummings3] or in this paper, however, do not seem to generalize to produce answers to Question 4 or any of the other above questions.
Acknowledgments
The author wishes to thank the referee for numerous helpful comments, suggestions, and corrections which considerably improved the exposition of the material contained herein. The author’s research was partially supported by PSC-CUNY Grant 63505-00-51.
