Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-23T04:05:30.304Z Has data issue: false hasContentIssue false
  • English
  • Français

Strong 0-1 laws in finite model theory

Published online by Cambridge University Press:  12 March 2014

Wafik Boulos Lotfallah
Wafik Boulos Lotfallah*
Affiliation:
Department of Mathematics, University of Wisconsin-Madison, Van Vleck Hall, 480 Lincoln Drive, Madison. WI 53706., USA, E-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce a new framework for asymptotic probabilities of sentences, in which we have a σ-additive measure on the sample space of all sequences A = {} of finite models, where the universe of 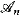is {1,2, …, n}. and use this framework to strengthen 0-1 laws for logics.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 65 , Issue 4 , December 2000 , pp. 1686 - 1704
Copyright
Copyright © Association for Symbolic Logic 2000

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Compton, K. J., 0-1 laws in logic and combinatorics, NATO advanced study institute on algorithms and order, 1987, pp. 353–383.Google Scholar
[2]Compton, K. J., A logical approach to asymptotic combinatorics I: first order properties. Advances in Mathematics, vol. 65 (1987), pp. 65–96.CrossRefGoogle Scholar
[3]Compton, K. J., The computational complexity of asymptotic problems I: partial orders, Information and Computation, vol. 78 (1988), pp. 108–123.CrossRefGoogle Scholar
[4]Compton, K. J., A logical approach to asymptotic combinatorics II: monadic second-order properties, Journal of Combinatorial Theory, Series A, vol. 50 (1989), pp. 110–131.CrossRefGoogle Scholar
[5]Fagin, R., Probabilities on finite models, this Journal, vol. 41 (1976), pp. 17–21.Google Scholar
[6]Glebskii, Y. V., Kogan, D. I., Liogonki, M. I., and Talanov, V. A., Range and degree of realizability of formulas in the restricted predicate calculus, Cybernetics, vol. 5 (1969), pp. 142–154.CrossRefGoogle Scholar
[7]Halmos, P. R., Measure theory, 1974.Google Scholar
[8]Hayman, W. K., A generalisation of Stirling's formula, Journal fuer angewandte undreine Mathematik, vol. 196 (1956), pp. 67–95.CrossRefGoogle Scholar
[9]Hella, L., Kolaitis, P. G., and Luosto, K., Almost everywhere equivalence of logics infinite model theory, The Bulletin of Symbolic Logic, vol. 2 (December 1996), no. 4, pp. 422–443.CrossRefGoogle Scholar
[10]Kleitman, D. J. and Rothschild, B. L., Asymptotic enumeration of partial orders on a finite set, Transactions of the American Mathematical Society, vol. 205 (1975), pp. 205–220.CrossRefGoogle Scholar
[11]Kolaitis, P. G. and Vardi, M. Y., Infinitary logics and 0-1 laws, Information and Computation, vol. 98 (1992), pp. 258–294, special issue: selections from the fifth annual IEEE symposium on logic in computer science.CrossRefGoogle Scholar
[12]Luczak, T. and Spencer, J., When does the zero-one law hold, Journal of the American Mathematical Society, vol. 4 (3) (1991), pp. 451–468.CrossRefGoogle Scholar
[13]Lynch, J. F.. Almost sure theories, Annals of Mathematical Logic, vol. 18 (1980), pp. 91–135.CrossRefGoogle Scholar
[14]Mycielski, J., Measure and category of some sets of models, Notices of the American Mathematical Society, vol. 22 (1975), pp. A–475.Google Scholar
[15]Oxtoby, J. C., Measure and category: A survey of the analogies between topological and measure spaces, 2n ded., Springer-Verlag, New York–Heidelberg–Berlin, 1980.CrossRefGoogle Scholar
[16]Shelah, S. and Spencer, J., Zero-one laws for sparse random graphs, Journal of the American Mathematical Society, vol. 1 (1988), pp. 97–115.CrossRefGoogle Scholar
[17]Williams, D., Probability with martingales, Cambridge University Press, 1991.CrossRefGoogle Scholar
[18]Problems infinite model theory, collected during the conference on Finite Model theory in Luminy, 1995, http://www.informatik.rwth-aachen.de/www-math/fmt.html.Google Scholar