Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T11:03:31.802Z Has data issue: false hasContentIssue false
  • English
  • Français

The Steel hierarchy of ordinal valued Borel mappings

Published online by Cambridge University Press:  12 March 2014

J. Duparc
J. Duparc*
Affiliation:
Equipe De Logique Mathémathique, CNRS Ura 753 et, Université Paris VII, U.F.R. De Mathématiques, 2 Place Jussieu, 75251 Paris Cedex 05, France, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given well ordered countable sets of the form Λϕ, we consider Borel mappings from Λϕω with countable image inside the ordinals. The ordinals and Λϕω are respectively equipped with the discrete topology and the product of the discrete topology on Λϕ. The Steel well-ordering on such mappings is denned by ϕ ≤ ψ iff there exists a continuous function f such that ϕ(x) ≤ ψof(x) holds for any x ϵ Λϕω. It induces a hierarchy of mappings which we give a complete description of. We provide, for each ordinal α, a mapping 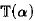whose rank is precisely α in this hierarchy and we also compute the height of the hierarchy restricted to mappings with image bounded by α. These mappings being viewed as partitions of the reals, there is, in most cases, a unique distinguished element of the partition. We analyze the relation between its topological complexity and the rank of the mapping in this hierarchy.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 68 , Issue 1 , March 2003 , pp. 187 - 234
Copyright
Copyright © Association for Symbolic Logic 2003

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Chalons, C., A unique integer associated to each map from Eω to ω, Comptes Rendas de l'Académie des Sciences. Série I Mathématique, vol. 331 (2000), no. 7, pp. 501–506.Google Scholar
[2]Duparc, J., Veblen Hierarchy and Wadge Hierarchy. Part I: Borel sets of finite rank, this Journal, vol. 66 (2001), no. 1, pp. 56–86.Google Scholar
[3]Duparc, J., Vehlen Hierarchy and Wadge Hierarchy, Part II: Borel sets of infinite rank, this Journal, submitted.Google Scholar
[4]van Engelen, F., Miller, A., and Steel, J., Rigid Borel sets and better quasi-order theory, Logic and combinatorics (Areata, Calif., 1985), American Mathematical Society, Providence, RI, 1987, pp. 199–222.CrossRefGoogle Scholar
[5]Gale, D. and Stewart, F.M., Infinite games with perfect information, Annals of Mathematics Studies, vol. 28 (1953), pp. 245–266.Google Scholar
[6]Louveau, A., Some results in the Wadge hierarchy of Borel sets, Cabal seminar 79–81, Springer, Berlin, 1983, Lecture Notes in Mathematics (1019), pp. 28–55.CrossRefGoogle Scholar
[7]Louveau, A. and Saint-Raymond, J., Les propriétés de réduction et de norme pour les classes de Boréliens, Fundamenta Mathematicae, vol. 131 (1988), pp. 223–243.CrossRefGoogle Scholar
[8]Louveau, A., The strength of Borel Wadge determinacy, Cabal seminar 81–85, Springer, Berlin, 1988, Lecture Notes in Mathematics (1333), pp. 1–30.Google Scholar
[9]Louveau, A., On the quasi-ordering of Borel linear orders under embeddability, this Journal, vol. 55 (1990), no. 2, pp. 537–560.Google Scholar
[10]Martin, D.A., Borel Determinacy, Annals of Mathematics, vol. 102 (1975), pp. 363–371.CrossRefGoogle Scholar
[11]Martin, D.A., A purely inductive proof of Borel determinacy, Recursion theory (Ithaca, N.Y., 1982), Proceedings of Symposia in Pure Mathematics, vol. 42, American Mathematical Society, Providence, RI, 1985, pp. 303–308.Google Scholar
[12]Sendak, M., Where the wild things are, Harper & Row, New York, 1963.Google Scholar
[13]Wadge, W.W., Degrees of complexity of subsets of the Baire space. Notice of the American Mathematical Society, 1972, A–714.Google Scholar
[14]Wadge, W.W., Reducibility and determinateness on the Baire space, Ph.D. thesis, Berkley, 1984.Google Scholar