Article contents
STABLY MEASURABLE CARDINALS
Published online by Cambridge University Press: 15 June 2020
Abstract
We define a weak iterability notion that is sufficient for a number of arguments concerning 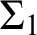 $\Sigma _{1}$
-definability at uncountable regular cardinals. In particular we give its exact consistency strength first in terms of the second uniform indiscernible for bounded subsets of
$\Sigma _{1}$
-definability at uncountable regular cardinals. In particular we give its exact consistency strength first in terms of the second uniform indiscernible for bounded subsets of 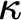 $\kappa $
:
$\kappa $
: 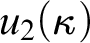 $u_2(\kappa )$
, and secondly to give the consistency strength of a property of Lücke’s.
$u_2(\kappa )$
, and secondly to give the consistency strength of a property of Lücke’s.
TheoremThe following are equiconsistent:
(i) There exists
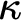 $\kappa $
which is stably measurable;
$\kappa $
which is stably measurable;(ii) for some cardinal
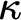 $\kappa $
,
$\kappa $
, 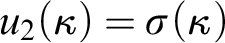 $u_2(\kappa )=\sigma (\kappa )$
;
$u_2(\kappa )=\sigma (\kappa )$
;(iii) The
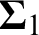 $\boldsymbol {\Sigma }_{1}$
-club property holds at a cardinal
$\boldsymbol {\Sigma }_{1}$
-club property holds at a cardinal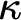 $\kappa $
.
$\kappa $
.
Here 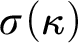 $\sigma (\kappa )$
is the height of the smallest
$\sigma (\kappa )$
is the height of the smallest 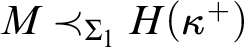 $M \prec _{\Sigma _{1}} H ( \kappa ^{+} )$
containing
$M \prec _{\Sigma _{1}} H ( \kappa ^{+} )$
containing 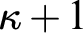 $\kappa +1$
and all of
$\kappa +1$
and all of 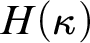 $H ( \kappa )$
. Let
$H ( \kappa )$
. Let 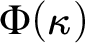 $\Phi (\kappa )$
be the assertion:
$\Phi (\kappa )$
be the assertion: 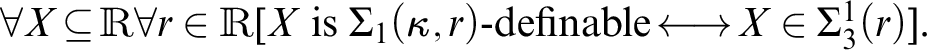
TheoremAssume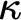 $\kappa $
is stably measurable. Then
$\kappa $
is stably measurable. Then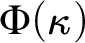 $\Phi (\kappa )$
.
$\Phi (\kappa )$
.
And a form of converse:
TheoremSuppose there is no sharp for an inner model with a strong cardinal. Then in the core model K we have: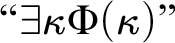 $\mbox {``}\exists \kappa \Phi (\kappa ) \mbox {''}$
is (set)-generically absolute
$\mbox {``}\exists \kappa \Phi (\kappa ) \mbox {''}$
is (set)-generically absolute ${\,\longleftrightarrow \,}$
There are arbitrarily large stably measurable cardinals.
${\,\longleftrightarrow \,}$
There are arbitrarily large stably measurable cardinals.
When 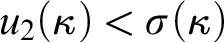 $u_2(\kappa ) < \sigma (\kappa )$
we give some results on inner model reflection.
$u_2(\kappa ) < \sigma (\kappa )$
we give some results on inner model reflection.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Association for Symbolic Logic 2020
References
- 2
- Cited by



