Hostname: page-component-848d4c4894-mwx4w Total loading time: 0 Render date: 2024-06-28T14:50:59.467Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability and posets

Published online by Cambridge University Press:  12 March 2014

Carl G. Jockusch Jr. ,
Bart Kastermans ,
Steffen Lempp ,
Manuel Lerman  and
Reed Solomon
Carl G. Jockusch Jr.
Affiliation:
University of Illinois, Department of Mathematics, Urbana, Il 61801-2975, USA, E-mail: [email protected]
Bart Kastermans
Affiliation:
University of Wisconsin, Department of Mathematics, Madison, Wi 53706-1388, USA, E-mail: [email protected], E-mail: [email protected]
Steffen Lempp
Affiliation:
University of Wisconsin, Department of Mathematics, Madison, Wi 53706-1388, USA, E-mail: [email protected], E-mail: [email protected]
Manuel Lerman
Affiliation:
University of Connecticut, Department of Mathematics, Storrs, Ct 06269-3009, USA, E-mail: [email protected], E-mail: [email protected]
Reed Solomon
Affiliation:
University of Connecticut, Department of Mathematics, Storrs, Ct 06269-3009, USA, E-mail: [email protected], E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Hirschfeldt and Shore have introduced a notion of stability for infinite posets. We define an arguably more natural notion called weak stability, and we study the existence of infinite computable or low chains or antichains, and of infinite 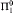chains and antichains, in infinite computable stable and weakly stable posets. For example, we extend a result of Hirschfeldt and Shore to show that every infinite computable weakly stable poset contains either an infinite low chain or an infinite computable antichain. Our hardest result is that there is an infinite computable weakly stable poset with no infinite 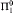chains or antichains. On the other hand, it is easily seen that every infinite computable stable poset contains an infinite computable chain or an infinite 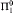antichain. In Reverse Mathematics, we show that SCAC, the principle that every infinite stable poset contains an infinite chain or antichain, is equivalent over RCA0 to WSAC, the corresponding principle for weakly stable posets.

Keywords

Primary: 03C57Secondary: 03D4506A06
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 74 , Issue 2 , June 2009 , pp. 693 - 711
Copyright
Copyright © Association for Symbolic Logic 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Cholak, Peter A., Jockusch, Carl G. Jr., and Slaman, Theodore A., On the strength of Ramsey's theorem for pairs, this Journal, vol. 66 (2001), pp. 1–55.Google Scholar
[2]Demuth, Oskar and Kučera, Antonín, Remarks on l-genericity, semigenericity, and related concepts, Commentationes Mathematicae Universitatis Carolinae, vol. 28 (1987), pp. 85–94.Google Scholar
[3]Harizanov, Valentina S., Jockusch, Carl G. Jr., and Knight, Julia F., Chains and antichains in partial orderings, Archive for Mathematical Logic, vol. 48 (2009), pp. 39–53.CrossRefGoogle Scholar
[4]Herrmann, Eberhard, Infinite chains and antichains in computable partial orderings, this Journal, vol. 66 (2001), pp. 923–934.Google Scholar
[5]Hirschfeldt, Denis R., Jockusch, Carl G. Jr, Kjos-Hanssen, Bjørn, Lempp, Steffen, and Slaman, Theodore A., The strength of some combinatorial principles related to Ramsey's theorem for pairs, Proceedings of the Program on Computational Prospects of Infinity (Chong, C. T., Feng, Qi, Slaman, Theodore, Woodin, Hugh, and Yang, Yue, editors), IMS Proceedings, World Scientific, 2007, pp. 143–161.Google Scholar
[6]Hirschfeldt, Denis R. and Shore, Richard A., >Combinatorial principles weaker than Ramsey's theorem for pairs, this Journal, vol. 72 (2007), pp. 171–206.Combinatorial+principles+weaker+than+Ramsey's+theorem+for+pairs,+this+Journal,+vol.+72+(2007),+pp.+171–206.>Google Scholar
[7]Hummel, Tamara L., Effective versions of Ramsey's theorem: Avoiding the cone above 0′, this Journal, vol. 59 (1994), pp. 1301–1325.Google Scholar
[8]Hummel, Tamara L. and Jockusch, Carl G. Jr., Generalized cohesiveness, this Journal, vol. 64 (1999), pp. 489–516.Google Scholar
[9]Jockusch, Carl G. Jr., Ramsey's theorem and recursion theory, this Journal, vol. 37 (1972), pp. 268–280.Google Scholar
[10]Rogers, Hartley Jr, Theory of Recursive Functions and Effective Computability, McGraw-Hill, New York-Toronto-London, 1967.Google Scholar
[11]Simpson, Stephen G., Subsystems of Second Order Arithmetic, Springer-Verlag, Berlin, Heidelberg, 1999.CrossRefGoogle Scholar