Article contents
SQUARES, ASCENT PATHS, AND CHAIN CONDITIONS
Published online by Cambridge University Press: 21 December 2018
Abstract
With the help of various square principles, we obtain results concerning the consistency strength of several statements about trees containing ascent paths, special trees, and strong chain conditions. Building on a result that shows that Todorčević’s principle 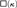 $\square \left( {\kappa ,\lambda } \right)$ implies an indexed version of
$\square \left( {\kappa ,\lambda } \right)$ implies an indexed version of 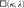 $\square \left( {\kappa ,\lambda } \right)$, we show that for all infinite, regular cardinals
$\square \left( {\kappa ,\lambda } \right)$, we show that for all infinite, regular cardinals 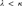 $\lambda < \kappa$, the principle
$\lambda < \kappa$, the principle 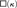 $\square \left( \kappa \right)$ implies the existence of a κ-Aronszajn tree containing a λ-ascent path. We then provide a complete picture of the consistency strengths of statements relating the interactions of trees with ascent paths and special trees. As a part of this analysis, we construct a model of set theory in which
$\square \left( \kappa \right)$ implies the existence of a κ-Aronszajn tree containing a λ-ascent path. We then provide a complete picture of the consistency strengths of statements relating the interactions of trees with ascent paths and special trees. As a part of this analysis, we construct a model of set theory in which  ${\aleph _2}$-Aronszajn trees exist and all such trees contain
${\aleph _2}$-Aronszajn trees exist and all such trees contain  ${\aleph _0}$-ascent paths. Finally, we use our techniques to show that the assumption that the κ-Knaster property is countably productive and the assumption that every κ-Knaster partial order is κ-stationarily layered both imply the failure of
${\aleph _0}$-ascent paths. Finally, we use our techniques to show that the assumption that the κ-Knaster property is countably productive and the assumption that every κ-Knaster partial order is κ-stationarily layered both imply the failure of 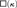 $\square \left( \kappa \right)$.
$\square \left( \kappa \right)$.
Keywords
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2018
References
REFERENCES
- 6
- Cited by


