Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Usuba, Toshimichi
2018.
New combinatorial principle on singular cardinals and normal ideals.
Mathematical Logic Quarterly,
Vol. 64,
Issue. 4-5,
p.
395.


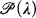
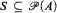 is said to be stationary in
is said to be stationary in 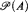 if for every
if for every 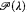 , if there is a regular uncountable cardinal
, if there is a regular uncountable cardinal 