Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-23T05:58:16.682Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectra of structures and relations

Published online by Cambridge University Press:  12 March 2014

Valentina S. Harizanov  and
Russell G. Miller
Valentina S. Harizanov
Affiliation:
Department of Mathematics, The George Washington University, Washington, DC 20052, USA. E-mail: [email protected] Department of Mathematics, Queens College– C.U.N.Y., 65-30 Kissena Blvd. Flushing, New York 11367, USA
Russell G. Miller
Affiliation:
PH.D. Program in Computer Science, The Graduate Center of C.U.N.Y., 365 Fifth Avenue, New York, New York 10016, USA. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider embeddings of structures which preserve spectra: if g : ℳ → 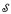with 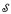computable, then ℳ should have the same Turing degree spectrum (as a structure) that g(ℳ) has (as a relation on 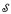). We show that the computable dense linear order ℒ is universal for all countable linear orders under this notion of embedding, and we establish a similar result for the computable random graph 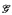Such structures are said to be spectrally universal. We use our results to answer a question of Goncharov, and also to characterize the possible spectra of structures as precisely the spectra of unary relations on 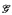. Finally, we consider the extent to which all spectra of unary relations on the structure ℒ may be realized by such embeddings, offering partial results and building the first known example of a structure whose spectrum contains precisely those degrees c with c′ ≥ τ 0″.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 72 , Issue 1 , March 2007 , pp. 324 - 348
Copyright
Copyright © Association for Symbolic Logic 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ash, C. J. and Knight, J., Computable structures and the hyperarithmetical hierarchy, Elsevier, Amsterdam, 2000.Google Scholar
[2]Chisholm, J., The complexity of intrinsically r.e. subsets of existentially decidable models, this Journal, vol. 55 (1990), pp. 1213–1232.Google Scholar
[3]Csima, B. F., Harizanov, V. S., Miller, R. G., and Montalbán, A., Computability of Fraïssé limits, to appear.Google Scholar
[4]Downey, R. G., Goncharov, S. S., and Hirschfeldt, D. R., Degree spectra for relations on Boolean algebras, Algebra and Logic, vol. 42 (2003), pp. 105–111.CrossRefGoogle Scholar
[5]Downey, R. G. and Jockusch, C. G., Every low Boolean algebra is isomorphic to a recursive one, Proceedings of the American Mathematical Society, vol. 122 (1994), pp. 871–880.CrossRefGoogle Scholar
[6]Downey, R. G. and Knight, J. F., Orderings with α-th jump degree 0(α), Proceedings of the American Mathematical Society, vol. 114 (1992), pp. 545–552.Google Scholar
[7]Goncharov, S. S., Harizanov, V. S., Knight, J. F., McCoy, C., Miller, R. G., and Solomon, R., Enumerations in computable structure theory, Annals of Pure and Applied Logic, vol. 136 (2005), pp. 219–246.CrossRefGoogle Scholar
[8]Harizanov, V. S., Uncountable degree spectra, Annals of Pure Applied Logic, vol. 54 (1991), pp. 255–263.CrossRefGoogle Scholar
[9]Harizanov, V. S., Pure computable model theory, Handbook of recursive mathematics, vol. 1, Studies in Logic and the Foundations of Mathematics, vol. 138, Elsevier, Amsterdam, 1998, pp. 3–114.Google Scholar
[10]Harizanov, V. S., Relations on computable structures, Contemporary mathematics (Bokan, N., editor), University of Belgrade, 2000, pp. 65–81.Google Scholar
[11]Hirschfeldt, D. R., Khoussainov, B., Shore, R. A., And Slinko, A. M., Degree spectra and computable dimensions in algebraic structures, Annals of Pure and Applied Logic, vol. 115 (2002), pp. 71–113.Google Scholar
[12]Hodges, W., A shorter model theory, Cambridge University Press, Cambridge, 1997.Google Scholar
[13]Jockusch, C. G. Jr. and Soare, R. I., Degrees of orderings not isomorphic to recursive linear orderings, Annals of Pure and Applied Logic, vol. 52 (1991), pp. 39–64.CrossRefGoogle Scholar
[14]Khoussainov, B. and Shore, R. A., Computable isomorphisms, degree spectra of relations, and Scott families, Annals of Pure and Applied Logic, vol. 93 (1998), pp. 153–193.CrossRefGoogle Scholar
[15]Khoussainov, B. and Shore, R. A., Effective model theory: the number of models and their complexity, Models and computability: Invited papers from logic colloquium '97 (Cooper, S.B. and Truss, J.K., editors), London Mathematical Society Lecture Note Series, vol. 259, Cambridge University Press, Cambridge, 1999, pp. 193–240.Google Scholar
[16]Knight, J. F., Degrees coded in jumps of orderings, this Journal, vol. 51 (1986), pp. 1034–1042.Google Scholar
[17]Miller, R., The -spectrum of a linear order, this Journal, vol. 66 (2001), pp. 470–486.Google Scholar
[18]Moses, M., Relations intrinsically recursive in linear orders, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 32 (1986), pp. 467–472.CrossRefGoogle Scholar
[19]Richter, L. J., Degrees of structures, this Journal, vol. 46 (1981), pp. 723–731.Google Scholar
[20]Soare, R. I., Recursively enumerable sets and degrees, Springer-Verlag, New York, 1987.CrossRefGoogle Scholar