Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-22T20:26:21.313Z Has data issue: false hasContentIssue false
  • English
  • Français

Spector forcing

Published online by Cambridge University Press:  12 March 2014

J. M. Henle
J. M. Henle*
Affiliation:
Smith College, Northampton, Massachusetts 01063
Get access Rights & Permissions [Opens in a new window]

Abstract

Forcing with [Κ]κ over a model of set theory with a strong partition cardinal, M. Spector produced a generic ultrafilter G on κ such that κκ/G is not well-founded.

Theorem. Let G be Spector-generic over a model M of 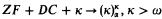, for all α < κ.

1) Every cardinal (well-ordered or not) of M is a cardinal of M[G].

2) If A ∈ M[G] is a well-ordered subset of M, then Ae M. Let Φ = Κκ/G.

3) There is an ultrafilter U on Φ such that every member of U has a subset of type Φ, and the intersection of any well-ordered subset of U is in U.

4) Φ satisfies 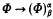for all α <ℵ1 and all ordinals β.

5) There is a linear order Φ′ with property 3) above which is not “weakly compact”, i.e., Φ′ ↛ (Φ′)2.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 49 , Issue 2 , June 1984 , pp. 542 - 554
Copyright
Copyright © Association for Symbolic Logic 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[H]Henle, J. M., Researches into the world of κ → (κ)κ, Annals of Mathematical Logic, vol. 17 (1979), pp. 151–169.CrossRefGoogle Scholar
[HMW]Henle, J. M., Mathias, A. R. D. and Woodin, H., A harren extension (to appear).Google Scholar
[H1]Kleinberg, E. M., Strong partition properties for infinite cardinals, this Journal, vol. 35 (1970), pp. 410–429.Google Scholar
[K2]Kleinberg, E. M., The ℵn are Jonsson cardinals and ℵω is a Rowbottom cardinal, Annals of Mathematical Logic, vol. 12 (1977), pp. 229–248.CrossRefGoogle Scholar
[K3]Kleinberg, E. M., Infinitary combinatorics and the axiom of determinateness, Lecture Note in Mathematics, vol. 612, Springer-Verlag, Berlin, 1977.CrossRefGoogle Scholar
[KS]Kleinberg, E. M. and Seiferas, J. I., Infinite exponent partition relations and well-ordered choice, this Journal, vol. 38 (1973), pp. 299–308.Google Scholar
[S]Spector, M., A measurable cardinal with a nonwellfounded ultrapower, this Journal, vol. 45 (1980), pp. 623–628.Google Scholar