Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T00:45:04.980Z Has data issue: false hasContentIssue false
  • English
  • Français

SOME QUESTIONS OF UNIFORMITY IN ALGORITHMIC RANDOMNESS

Part of: Computability and recursion theory

Published online by Cambridge University Press:  12 August 2021

LAURENT BIENVENU ,
BARBARA F. CSIMA  and
MATTHEW HARRISON-TRAINOR
LAURENT BIENVENU
Affiliation:
LABORATOIRE BORDELAIS DE RECHERCHE EN INFORMATIQUE CNRS, UNIVERSITÉ DE BORDEAUX BORDEAUX INP TALENCE, FRANCEE-mail: [email protected]
BARBARA F. CSIMA
Affiliation:
DEPARTMENT OF PURE MATHEMATICS UNIVERSITY OF WATERLOOWATERLOO, ON, CANADAE-mail: [email protected]
MATTHEW HARRISON-TRAINOR
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF MICHIGANANN ARBOR, MI, USAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The $\Omega $ numbers—the halting probabilities of universal prefix-free machines—are known to be exactly the Martin-Löf random left-c.e. reals. We show that one cannot uniformly produce, from a Martin-Löf random left-c.e. real 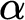$\alpha $ , a universal prefix-free machine U whose halting probability is 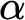$\alpha $ . We also answer a question of Barmpalias and Lewis-Pye by showing that given a left-c.e. 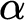real $\alpha $ , one cannot uniformly produce a left-c.e. real 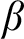$\beta $ such that 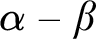$\alpha - \beta $ is neither left-c.e. nor right-c.e.

Keywords

algorithmic randomnessKolmogorov complexity

MSC classification

Primary: 03D32: Algorithmic randomness and dimension
Type
Article
Information
The Journal of Symbolic Logic , Volume 86 , Issue 4 , December 2021 , pp. 1612 - 1631
Check for updates
Copyright
© Association for Symbolic Logic 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ambos-Spies, K., Weihrauch, K., and Zheng, X., Weakly computable real numbers . Journal of Complexity, vol. 16 (2000), no. 4, pp. 676–690.10.1006/jcom.2000.0561CrossRefGoogle Scholar
Barmpalias, G., Aspects of Chaitin’s omega, Algorithmic Randomness: Progress and Prospects, Springer, Berlin, 2018, pp. 623–632.Google Scholar
Barmpalias, G. and Lewis-Pye, A., A note on the differences of computably enumerable reals, Computability and Complexity, Lecture Notes in Computational Sciences, vol. 10010, Springer, Cham, 2017, pp. 623–632.10.1007/978-3-319-50062-1_37CrossRefGoogle Scholar
Bienvenu, L. and Downey, R., Kolmogorov complexity and Solovay functions, Symposium on Theoretical Aspects of Computer Science (STACS 2009), Dagstuhl Seminar Proceedings, 09001, Schloss Dagstuhl—Leibniz-Zentrum fuer Informatik, Germany Internationales Begegnungs- und Forschungszentrum fuer Informatik (IBFI), Schloss Dagstuhl, 2009, pp. 147–158.Google Scholar
Bienvenu, L., Downey, R. G., Nies, A., and Merkle, W., Solovay functions and their applications in algorithmic randomness. Journal of Computer and System Sciences, vol. 81 (2015), no. 8, pp. 1575–1591.10.1016/j.jcss.2015.04.004CrossRefGoogle Scholar
Bienvenu, L. and Shen, A., Random semicomputable reals revisited, Computation, Physics and Beyond (M. J. Dinneen, B. Khoussainov, and A. Nies, editors), Lecture Notes in Computer Science, vol. 7160, Springer, Berlin, 2012, pp. 31–45.10.1007/978-3-642-27654-5_3CrossRefGoogle Scholar
Calude, C. S., Hertling, P. H., Khoussainov, B., and Wang, Y., Recursively enumerable reals and Chaitin $\varOmega$ numbers. Theoretical Computer Science, vol. 255 (2001), no. 1–2, pp. 125–149.10.1016/S0304-3975(99)00159-0CrossRefGoogle Scholar
Calude, C. S., Nies, A., Staiger, L., and Stephan, F.. Universal recursively enumerable sets of strings. Theoretical Computer Science, vol. 412 (2011), no. 22, pp. 2253–2261.10.1016/j.tcs.2011.01.002CrossRefGoogle Scholar
Calude, C. S. and Staiger, L., On universal computably enumerable prefix codes. Mathematical Structures Computer Science, vol. 19 (2009), no. 1, pp. 45–57.10.1017/S0960129508007238CrossRefGoogle Scholar
Chaitin, G. J., A theory of program size formally identical to information theory. Journal of the Association of the Computing Machinery, vol. 22 (1975), pp. 329–340.CrossRefGoogle Scholar
Downey, R. and Hirschfeldt, D.. Algorithmic Randomness and Complexity, Theory and Applications of Computability. Springer, Berlin, 2010.10.1007/978-0-387-68441-3CrossRefGoogle Scholar
Downey, R., Hirschfeldt, D. R., and Nies, A., Randomness, computability, and density. SIAM Journal on Computing, vol. 31 (2002), no. 4, pp. 1169–1183.10.1137/S0097539700376937CrossRefGoogle Scholar
Hoyrup, M. and Rojas, C., Computability of probability measures and Martin-Löf randomness over metric spaces. Information and Computation, vol. 207 (2009), no. 7, pp. 2207–2222.10.1016/j.ic.2008.12.009CrossRefGoogle Scholar
Kučera, A. and Slaman, T., Randomness and recursive enumerability. SIAM Journal on Computing, vol. 31 (2001), pp. 199–211.10.1137/S0097539799357441CrossRefGoogle Scholar
Ng, K. M., Some properties of d.c.e. reals and their degrees, Master’s thesis, National University of Singapore, 2006.Google Scholar
Nies, A., Computability and Randomness, Oxford Logic Guides, Oxford University Press, Oxford, 2009.10.1093/acprof:oso/9780199230761.001.0001CrossRefGoogle Scholar
Raichev, A., Relative randomness and real closed fields, this Journal, vol. 70 (2005), no. 1, pp. 319–330.Google Scholar
Solovay, R. M., Handwritten Manuscript Related to Chaitin’s Work. IBM Thomas J. Watson Research Center, Yorktown Heights, 1975, 215 pages.Google Scholar