No CrossRef data available.
Published online by Cambridge University Press: 23 October 2018
It is shown that 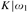 $K|{\omega _1}$ need not be solid in the sense previously introduced by the authors: it is consistent that there is no inner model with a Woodin cardinal yet there is an inner model W and a Cohen real x over W such that
$K|{\omega _1}$ need not be solid in the sense previously introduced by the authors: it is consistent that there is no inner model with a Woodin cardinal yet there is an inner model W and a Cohen real x over W such that 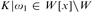 $K|{\omega _1}\,\, \in \,\,W[x] \setminus W$. However, if
$K|{\omega _1}\,\, \in \,\,W[x] \setminus W$. However, if 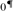 ${0^{\rm{\P}}}$ does not exist and
${0^{\rm{\P}}}$ does not exist and 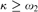 $\kappa \ge {\omega _2}$ is a cardinal, then
$\kappa \ge {\omega _2}$ is a cardinal, then 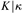 $K|\kappa$ is solid. We draw the conclusion that solidity is not forcing absolute in general, and that under the assumption of
$K|\kappa$ is solid. We draw the conclusion that solidity is not forcing absolute in general, and that under the assumption of 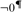 $\neg {0^{\rm{\P}}}$, the core model is contained in the solid core, previously introduced by the authors.
$\neg {0^{\rm{\P}}}$, the core model is contained in the solid core, previously introduced by the authors.
It is also shown, assuming 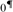 ${0^{\rm{\P}}}$ does not exist, that if there is a forcing that preserves
${0^{\rm{\P}}}$ does not exist, that if there is a forcing that preserves 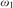 ${\omega _1}$, forces that every real has a sharp, and increases
${\omega _1}$, forces that every real has a sharp, and increases 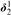 $\delta _2^1$, then
$\delta _2^1$, then 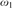 ${\omega _1}$ is measurable in K.
${\omega _1}$ is measurable in K.