Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T18:27:10.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Singular σ-dense trees

Published online by Cambridge University Press:  12 March 2014

Avner Landver
Avner Landver*
Affiliation:
Department of Mathematics, University of Kansas, Lawrence, Kansas 66045, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

Let 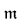be the least cardinal θ such that MAθ fails, 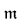(i.e. MA) implies that 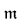is regular. Models for 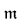regular with 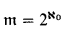are easy to get (see [Ku1]). Fremlin and Miller proved that cof(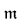) > ω [Fr, 41C(d)]. The question of whether it is consistent that 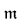be singular was solved, in the affirmative, by Kunen [Ku1]. Kunen used a (θ, θ) strong gap in 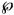(ω)/Fin, whose splitting partial order is c.c.c. He showed that if cof(θ) = ω1, and P is a c.c.c. partial order of cardinality < θ that may destroy the strong gap, then there exists another c.c.c. partial order Q, which does not destroy the strong gap, and such that ⊩Q “P is not c.c.c”. One then gets Kunen's model by iterating c.c.c. partial orders of cardinality < θ, without destroying the strong (θ, θ) gap. It is unknown whether it is consistent to have ω1 < cof() < .

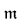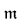Clearly, there exists a c.c.c. partial order Q with ∣Q∣ = 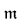, such that 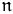(Q) = 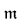(see (1.1)). A partial order P is σ-centered iff P is the union of countably many centered subsets, where a subset A ⊆ P is centered iff 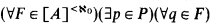p ≤ q. Clearly, a σ-centered partial order is c.c.c. Bell and Szymański proved that 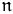(σ-centered) is regular (see [Be] or [Fr, 14C], and [Fr, 21K] or [vD, 3.1(e)]). This implies that if P is a σ-centered partial order, and 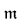is singular, then 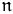(P) > 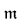. In particular, if 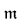is singular, then Q is not σ-centered and all c.c.c. partial orders of cardinality < 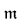have a Baire number (1.1) strictly greater than 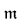. It was suggested in [Ku1] to try and use Q(T) (1.2), where T is a tree with no ω1-branches, to get models with singular 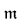. It is well known that when T is such a tree, the forcing Q(T) is c.c.c. [BMR], ∣Q(T)∣ = ∣T∣, and if T is not special, then n(Q(T)) ≤ ∣T∣.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 57 , Issue 4 , December 1992 , pp. 1403 - 1416
Copyright
Copyright © Association for Symbolic Logic 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[BcS]Balcar, B. and Simon, P., Disjoint refinement, Handbook of Boolean algebras, Vol. 2 (Monk, J. D. and Bonnet, R., editors), North-Holland, Amsterdam, 1989, pp. 333–386.Google Scholar
[BHK]Baumgartner, J. E., Harrington, L. A., and Kleinberg, E. M., Adding a closed unbounded set, this Journal, vol. 41 (1976), pp. 481–482.Google Scholar
[BMR]Baumgartner, J., Malitz, J., and Reinhardt, W., Embedding trees in the rationals, Proceedings of the National Academy of Sciences of the United States of America, vol. 67 (1970), pp. 1748–1753.CrossRefGoogle ScholarPubMed
[Be]Bell, M., On the combinatorial principle p(c), Fundamenta Mathematicae, vol. 114 (1981), pp. 149–159.CrossRefGoogle Scholar
[De]Devlin, K. J., ℵ1-trees, Annals of Mathematical Logic, vol. 13 (1978), pp. 267–330.CrossRefGoogle Scholar
[Fr]Fremlin, D., Consequences of Martin's axiom, Cambridge Tracts in Mathematics, vol. 84, Cambridge University Press, Cambridge, 1984.CrossRefGoogle Scholar
[ISh]Ihoda, J.Judah, H. and Shelah, S., Martin's axiom, measurability and equiconsistency, this Journal, vol. 54 (1989), pp. 78–94.Google Scholar
[J]Jech, T., Set theory, Academic Press, New York, 1978.Google Scholar
[J1]Jech, T., Some species of trees, Notices of the American Mathematical Society, vol. 19 (1972), p. A–29 (abstract 691–04–1).Google Scholar
[Ko]Koszmider, P., Semimorasses and nonreflection at singular cardinals, preprint.Google Scholar
[Ku]Kunen, K., Set theory, North-Holland, Amsterdam, 1980.Google Scholar
[Kul]Kunen, K., Where MA first fails, this Journal, vol. 53 (1988), pp. 429–433.Google Scholar
[KV]Kunen, K. and Vaughan, J. (editors), Handbook of set-theoretic topology, North-Holland, Amsterdam, 1984.Google Scholar
[Lan]Landver, A., Singular Baire numbers and related topics, Ph.D. thesis, University of Wisconsin, Madison, Wisconsin, 1990.Google Scholar
[Lav]Laver, R., Random reals and Souslin trees, Proceedings of the American Mathematical Society, vol. 100 (1987), pp. 531–534.CrossRefGoogle Scholar
[To]Todorčević, S., Trees and linearly ordered sets, in [KV], pp. 235–293.CrossRefGoogle Scholar
[Tol]Todorčević, S., Stationary sets, trees and continuums, Publications de l'Institut Mathématique [Beograd], Nouvelle Série, vol. 29 (43) (1981), pp. 249–262.Google Scholar
[vD]van Douwen, E. K., The integers and topology, in [KV], pp. 111–167.CrossRefGoogle Scholar
[We]Weiss, W., Versions of Martin's axiom, in [KV], pp. 827–886.CrossRefGoogle Scholar