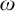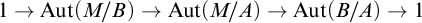1 Introduction and preliminaries
In Remarks on Galois cohomology and definability [Reference Pillay2], Anand Pillay introduced definable Galois cohomology, a model-theoretic generalization of the first nonabelian Galois cohomology set adapted for suitable first order theories T. When T is specialized to the theory
![]() $DCF_0$
, definable Galois cohomology coincides with constrained differential Galois cohomology as defined in Chapter 7 of Kolchin’s Differential Algebraic Groups [Reference Kolchin1]. When specialized to the theory
$DCF_0$
, definable Galois cohomology coincides with constrained differential Galois cohomology as defined in Chapter 7 of Kolchin’s Differential Algebraic Groups [Reference Kolchin1]. When specialized to the theory
![]() $ACF_0$
, definable Galois cohomology coincides with usual algebraic non-abelian Galois cohomology as defined in Chapter 1 Section 5 of Serre’s Galois Cohomology [Reference Serre5]. We begin by recalling the setting and main result of [Reference Pillay2] before stating our results. We will continue to work in this setting throughout this paper.
$ACF_0$
, definable Galois cohomology coincides with usual algebraic non-abelian Galois cohomology as defined in Chapter 1 Section 5 of Serre’s Galois Cohomology [Reference Serre5]. We begin by recalling the setting and main result of [Reference Pillay2] before stating our results. We will continue to work in this setting throughout this paper.
Let T be a complete theory eliminating imaginaries (or consider
![]() $T^{eq}$
). Let M be a model of T which is atomic and strongly
$T^{eq}$
). Let M be a model of T which is atomic and strongly
![]() $\omega $
-homogeneous over a set of parameters A. That is, the type of any finite tuple from M over A is isolated and for any two finite tuples from M with the same type over A, there is an automorphism of M taking one tuple to the other.
$\omega $
-homogeneous over a set of parameters A. That is, the type of any finite tuple from M over A is isolated and for any two finite tuples from M with the same type over A, there is an automorphism of M taking one tuple to the other.
Recall from [Reference Pillay2] that an (A-definable) right principal homogeneous space (PHS) for an A-definable group G is a nonempty A-definable set X together with a right A-definable action
![]() $\rho :X \times G \to X$
such that
$\rho :X \times G \to X$
such that
![]() $\forall x,y \in X$
there exists a unique
$\forall x,y \in X$
there exists a unique
![]() $z \in G$
such that
$z \in G$
such that
![]() $\rho (x,z) = y$
. A pointed PHS for G is a pair
$\rho (x,z) = y$
. A pointed PHS for G is a pair
![]() $(X,p)$
consisting of a PHS for G with a specified M-point p of X.
$(X,p)$
consisting of a PHS for G with a specified M-point p of X.
An A-definable bijection between two PHSs for G which commutes with the actions of G is an isomorphism of PHSs. The set of isomorphism classes of PHSs for G has the structure of a pointed set with basepoint being the isomorphism class containing G itself considered as a PHS. Altering slightly the notation from [Reference Pillay2], we will denote this pointed set
![]() $\operatorname {\mathrm {P}}_{\operatorname {\mathrm {def}}}(M/A,G(M))$
.
$\operatorname {\mathrm {P}}_{\operatorname {\mathrm {def}}}(M/A,G(M))$
.
Similarly, an A-definable bijection of two pointed PHSs for G commuting with the actions of G and which sends the basepoint of one to the basepoint of the other is an isomorphism of pointed PHSs. The set of A-isomorphism classes of pointed PHSs for G also has the structure of a pointed set. The basepoint is the isomorphism class containing the pointed PHS
![]() $(G,e)$
where e is the identity of G. We will denote this pointed set
$(G,e)$
where e is the identity of G. We will denote this pointed set
![]() $\operatorname {\mathrm {P}}_{\operatorname {\mathrm {def}},*}(M/A,G(M))$
.
$\operatorname {\mathrm {P}}_{\operatorname {\mathrm {def}},*}(M/A,G(M))$
.
A (right) definable cocycle is a function
![]() $\varphi $
from
$\varphi $
from
![]() $\operatorname {\mathrm {Aut}}(M/A)$
to
$\operatorname {\mathrm {Aut}}(M/A)$
to
![]() $G(M)$
, the M-points of G, such that firstly, for any
$G(M)$
, the M-points of G, such that firstly, for any
![]() $\sigma , \tau \in \operatorname {\mathrm {Aut}}(M/A)$
,
$\sigma , \tau \in \operatorname {\mathrm {Aut}}(M/A)$
,
and secondly, there exists an A-definable function
![]() $h(\bar {x},\bar {y})$
and tuple
$h(\bar {x},\bar {y})$
and tuple
![]() $\bar {a}$
from M such that
$\bar {a}$
from M such that
![]() $\forall \sigma \in \operatorname {\mathrm {Aut}}(M/A)$
,
$\forall \sigma \in \operatorname {\mathrm {Aut}}(M/A)$
,
The set of cocycles from
![]() $\operatorname {\mathrm {Aut}}(M/A)$
to
$\operatorname {\mathrm {Aut}}(M/A)$
to
![]() $G(M)$
is denoted
$G(M)$
is denoted
![]() $\operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(M/A,G(M))$
and has the structure of a pointed set. The cocycle which takes constant value at the identity
$\operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(M/A,G(M))$
and has the structure of a pointed set. The cocycle which takes constant value at the identity
![]() $e \in G(M)$
is the basepoint.
$e \in G(M)$
is the basepoint.
Two definable cocycles
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are said to be cohomologous if there is an element
$\psi $
are said to be cohomologous if there is an element
![]() $b \in G(M)$
such that
$b \in G(M)$
such that
for all
![]() $\sigma \in \operatorname {\mathrm {Aut}}(M/A)$
. Cohomology is an equivalence relation on the pointed set of cocycles,
$\sigma \in \operatorname {\mathrm {Aut}}(M/A)$
. Cohomology is an equivalence relation on the pointed set of cocycles,
![]() $\operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(M/A,G(M))$
, and a cocycle is called trivial if it is cohomologous to the constant cocycle. Taking the quotient of
$\operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(M/A,G(M))$
, and a cocycle is called trivial if it is cohomologous to the constant cocycle. Taking the quotient of
![]() $\operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(M/A,G(M))$
by the cohomology equivalence relation yields another pointed set, the pointed set of cohomology classes of cocycles, which is denoted
$\operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(M/A,G(M))$
by the cohomology equivalence relation yields another pointed set, the pointed set of cohomology classes of cocycles, which is denoted
![]() $\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
and which has the class of trivial cocycles as its basepoint.
$\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
and which has the class of trivial cocycles as its basepoint.
The main result of [Reference Pillay2] is the following:
Proposition 1.1. [Reference Pillay2, Proposition 3.3]
There is a natural isomorphism (basepoint preserving bijection, natural with respect to morphisms of definable groups in the second coordinate),
between the pointed set of isomorphism classes of A-definable right principal homogeneous spaces for G and
![]() $\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(M/A,G(M))$
, the pointed set of equivalence classes of definable cocycles from
$\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(M/A,G(M))$
, the pointed set of equivalence classes of definable cocycles from
![]() $\operatorname {\mathrm {Aut}}(M/A)$
to
$\operatorname {\mathrm {Aut}}(M/A)$
to
![]() $G(M)$
modulo the cohomology relation.
$G(M)$
modulo the cohomology relation.
An extension of parameters B, with
![]() $A \subseteq B \subseteq M$
, is called normal if it is closed under type (in finitely many variables) in M over A: Let
$A \subseteq B \subseteq M$
, is called normal if it is closed under type (in finitely many variables) in M over A: Let
![]() $\bar {b}$
be a finite tuple from B. If
$\bar {b}$
be a finite tuple from B. If
![]() $\bar {b}'$
is a finite tuple from M with
$\bar {b}'$
is a finite tuple from M with
![]() $\operatorname {\mathrm {tp}}(\bar {b}/A) = \operatorname {\mathrm {tp}}(\bar {b}'/A)$
then
$\operatorname {\mathrm {tp}}(\bar {b}/A) = \operatorname {\mathrm {tp}}(\bar {b}'/A)$
then
![]() $\bar {b}'$
must also be contained in B. By
$\bar {b}'$
must also be contained in B. By
![]() $\operatorname {\mathrm {Aut}}(B/A)$
we mean the group of elementary permutations of B fixing A. In Section 2 of this paper we will review normal extensions and describe some additional properties which they satisfy in the three settings of atomic and strongly
$\operatorname {\mathrm {Aut}}(B/A)$
we mean the group of elementary permutations of B fixing A. In Section 2 of this paper we will review normal extensions and describe some additional properties which they satisfy in the three settings of atomic and strongly
![]() $\omega $
-homogeneous structures discussed in [Reference Pillay2].
$\omega $
-homogeneous structures discussed in [Reference Pillay2].
In Section 3 of this paper we will define the definable Galois cohomology set
![]() $\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
where B is a normal extension of A in M and generalize the main result of [Reference Pillay2] to show that
$\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
where B is a normal extension of A in M and generalize the main result of [Reference Pillay2] to show that
![]() $\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
classifies exactly the isomorphism classes of PHS for G which contain a B-point.
$\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
classifies exactly the isomorphism classes of PHS for G which contain a B-point.
In [Reference Pillay3], Pillay adapted the notion of a (relatively) definable subset of
![]() $\operatorname {\mathrm {Aut}}(M/A)$
from the setting of a saturated model to that of an atomic and strongly
$\operatorname {\mathrm {Aut}}(M/A)$
from the setting of a saturated model to that of an atomic and strongly
![]() $\omega $
-homogeneous structure. This yields an equivalent definition of a definable cocycle (see [Reference Pillay3, Lemma 3.5]). Also in [Reference Pillay3], Pillay introduces (relatively) definable subsets of
$\omega $
-homogeneous structure. This yields an equivalent definition of a definable cocycle (see [Reference Pillay3, Lemma 3.5]). Also in [Reference Pillay3], Pillay introduces (relatively) definable subsets of
![]() $\operatorname {\mathrm {Aut}}(B/A)$
for normal extensions B of A in M. At the end of Section 3 below, we will show that our notion of definable cocycle, introduced at the beginning of Section 3 for the setting of a normal extension, has an equivalent phrasing using the definition of definable subset of
$\operatorname {\mathrm {Aut}}(B/A)$
for normal extensions B of A in M. At the end of Section 3 below, we will show that our notion of definable cocycle, introduced at the beginning of Section 3 for the setting of a normal extension, has an equivalent phrasing using the definition of definable subset of
![]() $\operatorname {\mathrm {Aut}}(B/A)$
from [Reference Pillay3].
$\operatorname {\mathrm {Aut}}(B/A)$
from [Reference Pillay3].
In Section 4 we will prove the main result of this paper: For B, a normal extension of A contained in M, a short exact sequence
induces the following short exact sequence in definable Galois cohomology:
We begin section 4 with an adaptation of Serre’s “transform” action of
![]() $\operatorname {\mathrm {Aut}}(B/A)$
on
$\operatorname {\mathrm {Aut}}(B/A)$
on
![]() $\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(M/B,G(M))$
to conclude that the image of the final map of the sequence lands in the fixed points of this action.
$\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(M/B,G(M))$
to conclude that the image of the final map of the sequence lands in the fixed points of this action.
The short exact sequence of the present paper is a generalization of a classical algebraic statement appearing in Chapter 1 Section 5.8 of Serre’s Galois Cohomology [Reference Serre5]. The result was proved by Kolchin in the differential setting as Theorem 1 of Chapter 7 Section 2 of [Reference Kolchin1]. Kolchin’s statement does not include mention of the action of
![]() $\operatorname {\mathrm {Aut}}(B/A)$
on the final term so we have strengthened the differential statement slightly. The result is novel in the general definable setting of [Reference Pillay2]. Together with the long exact sequence of [Reference Sánchez, Meretzky and Pillay4], our result brings definable Galois cohomology into a more fully developed state.
$\operatorname {\mathrm {Aut}}(B/A)$
on the final term so we have strengthened the differential statement slightly. The result is novel in the general definable setting of [Reference Pillay2]. Together with the long exact sequence of [Reference Sánchez, Meretzky and Pillay4], our result brings definable Galois cohomology into a more fully developed state.
2 Normal extensions
We continue in the setting of [Reference Pillay2]. Namely, T is a complete theory eliminating imaginaries. We work in a model M of T which is atomic and strongly
![]() $\omega $
-homogeneous over a set of parameters A.
$\omega $
-homogeneous over a set of parameters A.
The following definition precedes [Reference Tent and Ziegler6, Lemma 9.2.6].
Definition 2.1. An extension
![]() $A \subseteq B$
of parameters in M is said to be normal if, for any finite tuple
$A \subseteq B$
of parameters in M is said to be normal if, for any finite tuple
![]() $\bar {b}$
from B, every realization of
$\bar {b}$
from B, every realization of
![]() $\operatorname {\mathrm {tp}}(\bar {b}/A)$
in M is contained in B.
$\operatorname {\mathrm {tp}}(\bar {b}/A)$
in M is contained in B.
If B is a normal extension of A, then B is
![]() $\operatorname {\mathrm {Aut}}(M/A)$
-invariant and the restriction map from
$\operatorname {\mathrm {Aut}}(M/A)$
-invariant and the restriction map from
![]() $\operatorname {\mathrm {Aut}}(M/A)$
to
$\operatorname {\mathrm {Aut}}(M/A)$
to
![]() $\operatorname {\mathrm {Aut}}(B/A)$
, the group of elementary permutations of B fixing A, is a group homomorphism with kernel
$\operatorname {\mathrm {Aut}}(B/A)$
, the group of elementary permutations of B fixing A, is a group homomorphism with kernel
![]() $\operatorname {\mathrm {Aut}}(M/B)$
. So there is a short exact sequence
$\operatorname {\mathrm {Aut}}(M/B)$
. So there is a short exact sequence
In [Reference Pillay2], three model-theoretic settings are discussed in which the conditions on
![]() $A \subseteq M$
of atomicity and strong
$A \subseteq M$
of atomicity and strong
![]() $\omega $
-homogeneity are satisfied. These conditions ensure that Proposition 1.1 holds, i.e., that definable Galois cohomology classifies principal homogeneous spaces for definable groups.
$\omega $
-homogeneity are satisfied. These conditions ensure that Proposition 1.1 holds, i.e., that definable Galois cohomology classifies principal homogeneous spaces for definable groups.
In the first setting, M is taken to be the prime model over A of an
![]() $\omega $
-stable theory. In the second setting, M is taken to be
$\omega $
-stable theory. In the second setting, M is taken to be
![]() $\operatorname {\mathrm {acl}}(A)$
. In the third setting, M is the countable model of an
$\operatorname {\mathrm {acl}}(A)$
. In the third setting, M is the countable model of an
![]() $\omega $
-categorical theory. We will now address the assumptions on B needed in each setting so that the final map in the above sequence is surjective, that is, every elementary permutation of B fixing A extends to an automorphism of M fixing A.
$\omega $
-categorical theory. We will now address the assumptions on B needed in each setting so that the final map in the above sequence is surjective, that is, every elementary permutation of B fixing A extends to an automorphism of M fixing A.
When M is the model-theoretic algebraic closure of A or the prime model over A of an
![]() $\omega $
-stable theory, then for any normal extension B in M over A the restriction map from
$\omega $
-stable theory, then for any normal extension B in M over A the restriction map from
![]() $\operatorname {\mathrm {Aut}}(M/A)$
to
$\operatorname {\mathrm {Aut}}(M/A)$
to
![]() $\operatorname {\mathrm {Aut}}(B/A)$
is surjective. In the
$\operatorname {\mathrm {Aut}}(B/A)$
is surjective. In the
![]() $\omega $
-categorical setting
$\omega $
-categorical setting
![]() $B\backslash A$
must be finite for the restriction map to be surjective.
$B\backslash A$
must be finite for the restriction map to be surjective.
Remark 2.2. We slightly generalize the first setting of an
![]() $\omega $
-stable theory T to a totally transcendental theory T. Note that any
$\omega $
-stable theory T to a totally transcendental theory T. Note that any
![]() $\omega $
-stable theory is totally transcendental, the converse being true when T is countable.
$\omega $
-stable theory is totally transcendental, the converse being true when T is countable.
To see the surjectivity of the restriction map in the setting of the prime model of a totally transcendental theory, we use a fundamental characterization of such models which can be found in [Reference Tent and Ziegler6, Chapter 9]:
Fact 2.3. Let T be a totally transcendental theory. A model M of T is prime over a set of parameters A if and only if it is atomic over A and contains no uncountable A-indiscernible sequence.
Lemma 2.4. Let M be the prime model over A of a totally transcendental theory T. Let B be a normal extension over A in M. Then
-
(i) M is atomic over B.
-
(ii) M is prime over B.
-
(iii) The restriction homomorphism
 $\operatorname {\mathrm {Aut}}(M/A) \to \operatorname {\mathrm {Aut}}(B/A)$
is surjective.
$\operatorname {\mathrm {Aut}}(M/A) \to \operatorname {\mathrm {Aut}}(B/A)$
is surjective.
Proof.
-
(i) This can also be found in [Reference Tent and Ziegler6, Chapter 9]. Note that the isolated types are dense in the type space over arbitrary parameter sets in totally transcendental theories.
Let
 $\bar {b} \in M^n$
. Let
$\bar {b} \in M^n$
. Let
 $\phi (\bar {x})$
isolate
$\phi (\bar {x})$
isolate
 $\operatorname {\mathrm {tp}}(\bar {b}/A)$
. Since the isolated types are dense over B, there is a formula
$\operatorname {\mathrm {tp}}(\bar {b}/A)$
. Since the isolated types are dense over B, there is a formula
 $\psi (\bar {x},\bar {d})$
isolating a complete type over B which contains the formula
$\psi (\bar {x},\bar {d})$
isolating a complete type over B which contains the formula
 $\phi (\bar {x})$
. Let
$\phi (\bar {x})$
. Let
 $\bar {b}'$
realize
$\bar {b}'$
realize
 $\psi (\bar {x},\bar {d})$
in M. Then
$\psi (\bar {x},\bar {d})$
in M. Then
 $\bar {b}'$
realizes
$\bar {b}'$
realizes
 $\phi (\bar {x})$
and so
$\phi (\bar {x})$
and so
 $\bar {b}$
and
$\bar {b}$
and
 $\bar {b}'$
have the same type over A. By the strong
$\bar {b}'$
have the same type over A. By the strong
 $\omega $
-homogeneity of M there is an automorphism
$\omega $
-homogeneity of M there is an automorphism
 $\sigma $
of M taking
$\sigma $
of M taking
 $\bar {b}'$
to
$\bar {b}'$
to
 $\bar {b}$
. Let
$\bar {b}$
. Let
 $\bar {e} = \sigma (\bar {d})$
, which by normality must lie in B. Then
$\bar {e} = \sigma (\bar {d})$
, which by normality must lie in B. Then
 $\psi (\bar {x},\bar {e})$
isolates the type of
$\psi (\bar {x},\bar {e})$
isolates the type of
 $\bar {b}$
over B.
$\bar {b}$
over B. -
(ii) As
 $A \subseteq B$
, any B-indicernible sequence is A-indicernible. As M is prime over A, it contains no uncountable A-indicernible sequence and therefore no uncountable B-indicernible sequence. This, together with (i), shows from Fact 2.3 that M is prime over B.
$A \subseteq B$
, any B-indicernible sequence is A-indicernible. As M is prime over A, it contains no uncountable A-indicernible sequence and therefore no uncountable B-indicernible sequence. This, together with (i), shows from Fact 2.3 that M is prime over B. -
(iii) Let
 $\sigma $
be an elementary permutation of B over A. Let
$\sigma $
be an elementary permutation of B over A. Let
 $\bar {M}$
be a sufficiently saturated and strongly homogeneous model of T. Then we can assume that
$\bar {M}$
be a sufficiently saturated and strongly homogeneous model of T. Then we can assume that
 $\bar {M}$
contains M and that
$\bar {M}$
contains M and that
 $\sigma $
extends to an automorphism
$\sigma $
extends to an automorphism
 $\gamma \in \operatorname {\mathrm {Aut}}(\bar {M}/A)$
. Let
$\gamma \in \operatorname {\mathrm {Aut}}(\bar {M}/A)$
. Let
 $M' = \gamma (M)$
. By the characterization of prime models,
$M' = \gamma (M)$
. By the characterization of prime models,
 $M'$
is still the prime model over B. By the uniqueness of prime models of an
$M'$
is still the prime model over B. By the uniqueness of prime models of an
 $\omega $
-stable theory, there is an isomorphism
$\omega $
-stable theory, there is an isomorphism
 $\tau :M' \to M$
fixing B. Then
$\tau :M' \to M$
fixing B. Then
 $\tau \circ \gamma |_M:M \to M$
is an automorphism of M extending
$\tau \circ \gamma |_M:M \to M$
is an automorphism of M extending
 $\sigma $
.
$\sigma $
.
Proposition 2.5. Let B be normal in M over A where M is
![]() $\operatorname {\mathrm {acl}}(A)$
or the prime model of a totally transcendental theory or where M is
$\operatorname {\mathrm {acl}}(A)$
or the prime model of a totally transcendental theory or where M is
![]() $\omega $
-categorical and additionally we require
$\omega $
-categorical and additionally we require
![]() $B\backslash A$
to be finite. Then there is a short exact sequence of groups:
$B\backslash A$
to be finite. Then there is a short exact sequence of groups:
Proof. In the
![]() $\omega $
-categorical case the surjectivity follows from the strong
$\omega $
-categorical case the surjectivity follows from the strong
![]() $\omega $
-homogeneity of M and the fact that we have taken
$\omega $
-homogeneity of M and the fact that we have taken
![]() $B\backslash A$
to be finite. In the case where
$B\backslash A$
to be finite. In the case where
![]() $M = \operatorname {\mathrm {acl}}(A)$
, the surjectivity follows from a standard back and forth argument. The preceding lemma covers the case of the prime model of a totally transcendental theory.
$M = \operatorname {\mathrm {acl}}(A)$
, the surjectivity follows from a standard back and forth argument. The preceding lemma covers the case of the prime model of a totally transcendental theory.
3 Definable Galois cohomology for normal extensions
We continue to work in the setting of [Reference Pillay2]. Let T be a complete theory eliminating imaginaries (EI). Let M be a model of T containing a set of parameters A, over which M is atomic and strongly
![]() $\omega $
-homogeneous.
$\omega $
-homogeneous.
Let B be a normal extension of A in M such that elementary permutations of B over A (which we denote
![]() $\operatorname {\mathrm {Aut}}(B/A)$
) extend to automorphisms of M over A and such that M is atomic and strongly
$\operatorname {\mathrm {Aut}}(B/A)$
) extend to automorphisms of M over A and such that M is atomic and strongly
![]() $\omega $
-homogeneous over B. We have in mind the three model-theoretic settings of [Reference Pillay2] discussed in the last section: i.e., when M is the prime model over A of a totally transcendental theory or M is
$\omega $
-homogeneous over B. We have in mind the three model-theoretic settings of [Reference Pillay2] discussed in the last section: i.e., when M is the prime model over A of a totally transcendental theory or M is
![]() $\operatorname {\mathrm {acl}}(A)$
then any normal intermediate extension B will satisfy these conditions. When M is the countable model of an
$\operatorname {\mathrm {acl}}(A)$
then any normal intermediate extension B will satisfy these conditions. When M is the countable model of an
![]() $\omega $
-categorical theory,
$\omega $
-categorical theory,
![]() $B\backslash A$
must be finite in addition to B being normal.
$B\backslash A$
must be finite in addition to B being normal.
By the atomicity and strong
![]() $\omega $
-homogeneity of M over B, we have that an M-definable
$\omega $
-homogeneity of M over B, we have that an M-definable
![]() $\operatorname {\mathrm {Aut}}(M/B)$
-invariant set is B-definable, from which it follows that the fixed set of the action of
$\operatorname {\mathrm {Aut}}(M/B)$
-invariant set is B-definable, from which it follows that the fixed set of the action of
![]() $\operatorname {\mathrm {Aut}}(M/B)$
on M is
$\operatorname {\mathrm {Aut}}(M/B)$
on M is
![]() $\operatorname {\mathrm {dcl}}(B)$
.
$\operatorname {\mathrm {dcl}}(B)$
.
Definition 3.1. Let G be an A-definable group and X an A-definable set. Let
![]() $\varphi (\bar {x})$
and
$\varphi (\bar {x})$
and
![]() $\psi (\bar {y})$
be A-formulas defining the underlying set of G and X respectively. By
$\psi (\bar {y})$
be A-formulas defining the underlying set of G and X respectively. By
![]() $G(B)$
we mean
$G(B)$
we mean
or equivalently,
![]() $G(M) \cap B^{|\bar {x}|}$
. Similarly, by
$G(M) \cap B^{|\bar {x}|}$
. Similarly, by
![]() $X(B)$
we mean
$X(B)$
we mean
equivalently,
![]() $X(M)\cap B^{|\bar {y}|}$
. We will refer to elements of
$X(M)\cap B^{|\bar {y}|}$
. We will refer to elements of
![]() $G(B)$
and
$G(B)$
and
![]() $X(B)$
as B-points of
$X(B)$
as B-points of
![]() $G(M)$
and
$G(M)$
and
![]() $X(M)$
.
$X(M)$
.
We will also now require
![]() $B = \operatorname {\mathrm {dcl}}(B)$
for two reasons, firstly, so that B is exactly the fixed set of the action of
$B = \operatorname {\mathrm {dcl}}(B)$
for two reasons, firstly, so that B is exactly the fixed set of the action of
![]() $\operatorname {\mathrm {Aut}}(M/B)$
on M and secondly, so that
$\operatorname {\mathrm {Aut}}(M/B)$
on M and secondly, so that
![]() $G(B)$
is a subgroup of
$G(B)$
is a subgroup of
![]() $G(M)$
.
$G(M)$
.
Lemma 3.2. Let G be an A-definable group. Let
![]() $A \subseteq B \subseteq M$
with
$A \subseteq B \subseteq M$
with
![]() $B = \operatorname {\mathrm {dcl}}(B)$
. Then
$B = \operatorname {\mathrm {dcl}}(B)$
. Then
![]() $G(B)$
is an abstract subgroup of
$G(B)$
is an abstract subgroup of
![]() $G(M)$
. Moreover, if X is an A-definable principal homogeneous space for G which contains a B-point, then
$G(M)$
. Moreover, if X is an A-definable principal homogeneous space for G which contains a B-point, then
![]() $X(B)$
is an abstract principal homogeneous space for
$X(B)$
is an abstract principal homogeneous space for
![]() $G(B)$
equivariant with respect to the left action of
$G(B)$
equivariant with respect to the left action of
![]() $\operatorname {\mathrm {Aut}}(B/A)$
.
$\operatorname {\mathrm {Aut}}(B/A)$
.
Proof. Again, let
![]() $\varphi (\bar {x})$
and
$\varphi (\bar {x})$
and
![]() $\psi (\bar {y})$
be A-formulas defining the underlying set of G and X respectively.
$\psi (\bar {y})$
be A-formulas defining the underlying set of G and X respectively.
Let
![]() $e \in G$
be the identity. As G is A-definable,
$e \in G$
be the identity. As G is A-definable,
![]() $e \in G(\operatorname {\mathrm {dcl}}(A)) \subseteq G(B)$
. Let
$e \in G(\operatorname {\mathrm {dcl}}(A)) \subseteq G(B)$
. Let
![]() $g_1,g_2 \in G(B)$
. Their product
$g_1,g_2 \in G(B)$
. Their product
![]() $g_1g_2$
is definable over
$g_1g_2$
is definable over
![]() $A\cup \{g_1, g_2\}$
, that is
$A\cup \{g_1, g_2\}$
, that is
![]() $g_1g_2 \in \operatorname {\mathrm {dcl}}(A,g_1,g_2)$
and so must lie in
$g_1g_2 \in \operatorname {\mathrm {dcl}}(A,g_1,g_2)$
and so must lie in
![]() $\operatorname {\mathrm {dcl}}(B)$
as
$\operatorname {\mathrm {dcl}}(B)$
as
![]() $\operatorname {\mathrm {dcl}}(B) = B$
. We have
$\operatorname {\mathrm {dcl}}(B) = B$
. We have
![]() $g_1g_2 \in B^{|\bar {x}|} \cap G(M) = G(B)$
. Likewise,
$g_1g_2 \in B^{|\bar {x}|} \cap G(M) = G(B)$
. Likewise,
![]() $g_1^{-1}$
is definable over
$g_1^{-1}$
is definable over
![]() $\operatorname {\mathrm {dcl}}(A,g_1)$
, so
$\operatorname {\mathrm {dcl}}(A,g_1)$
, so
![]() $g_1^{-1} \in B^{|\bar {x}|} \cap G(M) = G(B)$
. Hence
$g_1^{-1} \in B^{|\bar {x}|} \cap G(M) = G(B)$
. Hence
![]() $G(B)$
is an abstract subgroup of
$G(B)$
is an abstract subgroup of
![]() $G(M)$
.
$G(M)$
.
By assumption
![]() $X(B) \neq \emptyset $
, so let
$X(B) \neq \emptyset $
, so let
![]() $p \in X(B)$
. Let
$p \in X(B)$
. Let
![]() $g \in G(B)$
, then
$g \in G(B)$
, then
![]() $pg \in \operatorname {\mathrm {dcl}}(A,p,g)$
. As
$pg \in \operatorname {\mathrm {dcl}}(A,p,g)$
. As
![]() $\operatorname {\mathrm {dcl}}(A,p,g) \subseteq \operatorname {\mathrm {dcl}}(B) = B$
,
$\operatorname {\mathrm {dcl}}(A,p,g) \subseteq \operatorname {\mathrm {dcl}}(B) = B$
,
![]() $pg \in B^{|\bar {y}|}$
. Hence
$pg \in B^{|\bar {y}|}$
. Hence
![]() $pg \in X(B)$
. So
$pg \in X(B)$
. So
![]() $G(B)$
acts on
$G(B)$
acts on
![]() $X(B)$
. Now let
$X(B)$
. Now let
![]() $p' \in X(B)$
. As X is an A-definable PHS for G, there is a unique element
$p' \in X(B)$
. As X is an A-definable PHS for G, there is a unique element
![]() $g \in G(M)$
such that
$g \in G(M)$
such that
![]() $pg = g'$
. So
$pg = g'$
. So
![]() $g \in \operatorname {\mathrm {dcl}}(A,p,p')$
. As
$g \in \operatorname {\mathrm {dcl}}(A,p,p')$
. As
![]() $\operatorname {\mathrm {dcl}}(A,p,p') \subseteq \operatorname {\mathrm {dcl}}(B) = B$
,
$\operatorname {\mathrm {dcl}}(A,p,p') \subseteq \operatorname {\mathrm {dcl}}(B) = B$
,
![]() $g \in B^{|\bar {x}|}$
. Hence
$g \in B^{|\bar {x}|}$
. Hence
![]() $g \in G(B)$
. So
$g \in G(B)$
. So
![]() $X(B)$
is an abstract PHS for
$X(B)$
is an abstract PHS for
![]() $G(B)$
.
$G(B)$
.
Let
![]() $\sigma \in \operatorname {\mathrm {Aut}}(B/A)$
. Let
$\sigma \in \operatorname {\mathrm {Aut}}(B/A)$
. Let
![]() $p \in X(B)$
and
$p \in X(B)$
and
![]() $g \in G(B)$
then
$g \in G(B)$
then
![]() $\sigma (pg) = \sigma (p)\sigma (g)$
as the action is A-definable and
$\sigma (pg) = \sigma (p)\sigma (g)$
as the action is A-definable and
![]() $\sigma $
is an A-elementary permutation of B. So the equivariance of the action is verified.
$\sigma $
is an A-elementary permutation of B. So the equivariance of the action is verified.
In this section we will define definable Galois cohomology in the setting of a normal extension
![]() $A \subseteq B$
and introduce the notation
$A \subseteq B$
and introduce the notation
![]() $\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
. We then introduce some further notation for certain pointed sets of isomorphism classes of definable PHSs. We then prove that
$\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
. We then introduce some further notation for certain pointed sets of isomorphism classes of definable PHSs. We then prove that
![]() $\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
classifies exactly the isomorphism classes of definable PHSs for G which contain a B-point. This refines Proposition 1.1, the main result of [Reference Pillay2], to apply in the setting of normal intermediate extensions.
$\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
classifies exactly the isomorphism classes of definable PHSs for G which contain a B-point. This refines Proposition 1.1, the main result of [Reference Pillay2], to apply in the setting of normal intermediate extensions.
Definition 3.3. A definable (right) cocycle
![]() $\varphi :\operatorname {\mathrm {Aut}}(B/A) \to G(B)$
is a function
$\varphi :\operatorname {\mathrm {Aut}}(B/A) \to G(B)$
is a function
![]() $\varphi $
together with an A-definable function
$\varphi $
together with an A-definable function
![]() $h(\bar {x},\bar {y})$
and a tuple
$h(\bar {x},\bar {y})$
and a tuple
![]() $\bar {a}$
from B satisfying
$\bar {a}$
from B satisfying
![]() $\forall \sigma , \tau \in \operatorname {\mathrm {Aut}}(B/A)$
,
$\forall \sigma , \tau \in \operatorname {\mathrm {Aut}}(B/A)$
,
-
(i)
 $\varphi (\sigma \tau ) = \varphi (\sigma )\sigma (\varphi (\tau ))$
(cocycle condition)
$\varphi (\sigma \tau ) = \varphi (\sigma )\sigma (\varphi (\tau ))$
(cocycle condition) -
(ii)
 $\varphi (\sigma ) = h(\bar {a},\sigma (\bar {a}))$
(definability condition)
$\varphi (\sigma ) = h(\bar {a},\sigma (\bar {a}))$
(definability condition)
The definable cocycles from
![]() $\operatorname {\mathrm {Aut}}(B/A)$
to
$\operatorname {\mathrm {Aut}}(B/A)$
to
![]() $G(B)$
form a pointed set, which we denote
$G(B)$
form a pointed set, which we denote
![]() $Z^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
. We define the basepoint of
$Z^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
. We define the basepoint of
![]() $Z^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
to be the constant cocycle which sends every elementary permutation to the identity of G.
$Z^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
to be the constant cocycle which sends every elementary permutation to the identity of G.
Two definable cocycles
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are said to be cohomologous if there is an element
$\psi $
are said to be cohomologous if there is an element
![]() $b \in G(B)$
such that
$b \in G(B)$
such that
for all
![]() $\sigma \in \operatorname {\mathrm {Aut}}(B/A)$
. As we required B to be
$\sigma \in \operatorname {\mathrm {Aut}}(B/A)$
. As we required B to be
![]() $\operatorname {\mathrm {dcl}}$
-closed,
$\operatorname {\mathrm {dcl}}$
-closed,
![]() $G(B)$
is a group and cohomology is again an equivalence relation on
$G(B)$
is a group and cohomology is again an equivalence relation on
![]() $\operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
. Again we call a cocycle trivial if it is cohomologous to the constant cocycle. Trivial cocycles are therefore of the form
$\operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
. Again we call a cocycle trivial if it is cohomologous to the constant cocycle. Trivial cocycles are therefore of the form
for some
![]() $b \in G(B)$
. The quotient of
$b \in G(B)$
. The quotient of
![]() $\operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
via the cohomology equivalence relation is again a pointed set which we denote
$\operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
via the cohomology equivalence relation is again a pointed set which we denote
![]() $\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
and which has the class of trivial cocycles as its basepoint.
$\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
and which has the class of trivial cocycles as its basepoint.
We now describe the relationship between the pointed sets
![]() $\operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
and
$\operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
and
![]() $\operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(M/A,G(M))$
. Let
$\operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(M/A,G(M))$
. Let
![]() $\pi :\operatorname {\mathrm {Aut}}(M/A) \to \operatorname {\mathrm {Aut}}(B/A)$
be the projection homomorphism which via our assumptions is surjective.
$\pi :\operatorname {\mathrm {Aut}}(M/A) \to \operatorname {\mathrm {Aut}}(B/A)$
be the projection homomorphism which via our assumptions is surjective.
Lemma 3.4. Let
![]() $\varphi \in \operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
, then
$\varphi \in \operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
, then
defined by
![]() $\varphi \mapsto \varphi \circ \pi $
is an injective map of pointed sets whose image is exactly the set of definable cocycles in
$\varphi \mapsto \varphi \circ \pi $
is an injective map of pointed sets whose image is exactly the set of definable cocycles in
![]() $\operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(M/A,G(M))$
which have definability parameter
$\operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(M/A,G(M))$
which have definability parameter
![]() $\bar {a}$
in B. Moreover
$\bar {a}$
in B. Moreover
![]() $-\circ \pi $
descends to an injective map on cohomology,
$-\circ \pi $
descends to an injective map on cohomology,
Proof. Let
![]() $\varphi $
be a definable cocycle from
$\varphi $
be a definable cocycle from
![]() $\operatorname {\mathrm {Aut}}(B/A)$
to
$\operatorname {\mathrm {Aut}}(B/A)$
to
![]() $G(B)$
with definability data
$G(B)$
with definability data
![]() $h(\bar {x},\bar {y})$
and
$h(\bar {x},\bar {y})$
and
![]() $\bar {a}$
in B. We first check that
$\bar {a}$
in B. We first check that
![]() $\varphi \circ \pi $
is still a cocycle witnessed by the same definability data:
$\varphi \circ \pi $
is still a cocycle witnessed by the same definability data:
Let
![]() $\sigma , \tau \in \operatorname {\mathrm {Aut}}(M/A)$
,
$\sigma , \tau \in \operatorname {\mathrm {Aut}}(M/A)$
,
 $$ \begin{align*} \varphi \circ \pi(\sigma\tau) &= \varphi(\pi(\sigma)\cdot \pi(\tau))\\ &= \varphi(\pi(\sigma))\cdot \pi(\sigma)(\varphi(\pi(\tau)))\\ &= \varphi\circ \pi(\sigma)\cdot \sigma(\varphi\circ \pi(\tau)). \end{align*} $$
$$ \begin{align*} \varphi \circ \pi(\sigma\tau) &= \varphi(\pi(\sigma)\cdot \pi(\tau))\\ &= \varphi(\pi(\sigma))\cdot \pi(\sigma)(\varphi(\pi(\tau)))\\ &= \varphi\circ \pi(\sigma)\cdot \sigma(\varphi\circ \pi(\tau)). \end{align*} $$
So the cocycle condition is satisfied. For the definability condition, let
![]() $\sigma \in \operatorname {\mathrm {Aut}}(M/A)$
. As
$\sigma \in \operatorname {\mathrm {Aut}}(M/A)$
. As
![]() $\bar {a}$
is in B,
$\bar {a}$
is in B,
Since
![]() $\pi $
is surjective, the map
$\pi $
is surjective, the map
![]() $-\circ \pi $
on cocycles is injective.
$-\circ \pi $
on cocycles is injective.
Let
![]() $\varphi \in \operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(M/A,G(M))$
with definability parameter
$\varphi \in \operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(M/A,G(M))$
with definability parameter
![]() $\bar {a}$
coming from B. Let
$\bar {a}$
coming from B. Let
![]() $\sigma \in \operatorname {\mathrm {Aut}}(M/A)$
. The definability condition
$\sigma \in \operatorname {\mathrm {Aut}}(M/A)$
. The definability condition
![]() $\varphi (\sigma ) = h(\bar {a},\sigma (\bar {a}))$
shows that
$\varphi (\sigma ) = h(\bar {a},\sigma (\bar {a}))$
shows that
![]() $\varphi (\sigma ) \in \operatorname {\mathrm {dcl}}(\bar {a}, \sigma (\bar {a}))$
. By the normality of B and the assumption that B is
$\varphi (\sigma ) \in \operatorname {\mathrm {dcl}}(\bar {a}, \sigma (\bar {a}))$
. By the normality of B and the assumption that B is
![]() $\operatorname {\mathrm {dcl}}$
-closed, we obtain
$\operatorname {\mathrm {dcl}}$
-closed, we obtain
![]() $\varphi (\sigma ) \in G(B)$
. Furthermore, as
$\varphi (\sigma ) \in G(B)$
. Furthermore, as
![]() $\bar {a}$
comes from B and
$\bar {a}$
comes from B and
![]() $\varphi (\sigma ) = h(\bar {a},\sigma (\bar {a}))$
,
$\varphi (\sigma ) = h(\bar {a},\sigma (\bar {a}))$
,
![]() $\varphi (\sigma )$
depends only on the restriction
$\varphi (\sigma )$
depends only on the restriction
![]() $\pi (\sigma )$
and so descends to a well defined map on
$\pi (\sigma )$
and so descends to a well defined map on
![]() $\operatorname {\mathrm {Aut}}(B/A)$
which we call
$\operatorname {\mathrm {Aut}}(B/A)$
which we call
![]() $\tilde {\varphi }$
. As
$\tilde {\varphi }$
. As
![]() $\tilde {\varphi }$
and
$\tilde {\varphi }$
and
![]() $\varphi $
have the same image, it is clear that
$\varphi $
have the same image, it is clear that
![]() $\tilde {\varphi } \in \operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
as witnessed by the same definability data. Lastly,
$\tilde {\varphi } \in \operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
as witnessed by the same definability data. Lastly,
![]() $\tilde {\varphi }\circ \pi = \varphi $
. So the image of
$\tilde {\varphi }\circ \pi = \varphi $
. So the image of
![]() $\operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
under
$\operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
under
![]() $-\circ \pi $
is exactly the subset of definable cocycles in
$-\circ \pi $
is exactly the subset of definable cocycles in
![]() $\operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(M/A,G(M))$
which have definability parameter
$\operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(M/A,G(M))$
which have definability parameter
![]() $\bar {a}$
in B.
$\bar {a}$
in B.
Let
![]() $\varphi _1$
and
$\varphi _1$
and
![]() $\varphi _2$
in
$\varphi _2$
in
![]() $Z^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
be cohomologous as witnessed by
$Z^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
be cohomologous as witnessed by
![]() $g \in G(B)$
. As
$g \in G(B)$
. As
![]() $G(B) \subseteq G(M)$
, the same element g witnesses that
$G(B) \subseteq G(M)$
, the same element g witnesses that
![]() $\varphi _1 \circ \pi $
and
$\varphi _1 \circ \pi $
and
![]() $\varphi _2 \circ \pi $
are cohomologous. So the map on cocycles descends to a well defined map on cohomology which we call
$\varphi _2 \circ \pi $
are cohomologous. So the map on cocycles descends to a well defined map on cohomology which we call
![]() $\pi ^*$
.
$\pi ^*$
.
Let
![]() $\varphi _1$
and
$\varphi _1$
and
![]() $\varphi _2$
be cocycles from
$\varphi _2$
be cocycles from
![]() $\operatorname {\mathrm {Aut}}(B/A)$
to
$\operatorname {\mathrm {Aut}}(B/A)$
to
![]() $G(B)$
with definability data
$G(B)$
with definability data
![]() $h_1$
,
$h_1$
,
![]() $\bar {a}_1$
and
$\bar {a}_1$
and
![]() $h_2$
,
$h_2$
,
![]() $\bar {a}_2$
respectively. Suppose that
$\bar {a}_2$
respectively. Suppose that
![]() $\varphi _1 \circ \pi $
and
$\varphi _1 \circ \pi $
and
![]() $\varphi _2\circ \pi $
are cohomologous via
$\varphi _2\circ \pi $
are cohomologous via
![]() $g \in G(M)$
. So for all
$g \in G(M)$
. So for all
![]() $\sigma \in \operatorname {\mathrm {Aut}}(M/A)$
,
$\sigma \in \operatorname {\mathrm {Aut}}(M/A)$
,
As
![]() $\bar {a}_1$
and
$\bar {a}_1$
and
![]() $\bar {a}_2$
lie in B, for all
$\bar {a}_2$
lie in B, for all
![]() $\sigma \in \operatorname {\mathrm {Aut}}(M/B)$
we have
$\sigma \in \operatorname {\mathrm {Aut}}(M/B)$
we have
![]() $h(\bar {a}_1,\sigma (\bar {a}_1)) = e$
and
$h(\bar {a}_1,\sigma (\bar {a}_1)) = e$
and
![]() $h(\bar {a}_2,\sigma (\bar {a}_2)) = e$
and therefore
$h(\bar {a}_2,\sigma (\bar {a}_2)) = e$
and therefore
![]() $g^{-1}\sigma (g) = e$
. So g is fixed by the action of
$g^{-1}\sigma (g) = e$
. So g is fixed by the action of
![]() $\operatorname {\mathrm {Aut}}(M/B)$
. Then as
$\operatorname {\mathrm {Aut}}(M/B)$
. Then as
![]() $B = \operatorname {\mathrm {dcl}}(B)$
, we have
$B = \operatorname {\mathrm {dcl}}(B)$
, we have
![]() $g \in G(B)$
. So the same g witnesses that
$g \in G(B)$
. So the same g witnesses that
![]() $\varphi _1$
and
$\varphi _1$
and
![]() $\varphi _2$
are cohomologous. We have then shown that the induced map on cohomology,
$\varphi _2$
are cohomologous. We have then shown that the induced map on cohomology,
![]() $\pi ^*$
, is injective.
$\pi ^*$
, is injective.
We now alter and extend slightly the notation from [Reference Pillay2] for pointed sets of isomorphism classes of definable PHSs. We first make some observations.
As B is
![]() $\operatorname {\mathrm {dcl}}$
-closed, if
$\operatorname {\mathrm {dcl}}$
-closed, if
![]() $X_1$
and
$X_1$
and
![]() $X_2$
are isomorphic A-definable PHSs for an A-definable group G then
$X_2$
are isomorphic A-definable PHSs for an A-definable group G then
![]() $X_1$
has a B-point if and only if
$X_1$
has a B-point if and only if
![]() $X_2$
has a B-point. Moreover, if
$X_2$
has a B-point. Moreover, if
![]() $(X_1,p_1)$
and
$(X_1,p_1)$
and
![]() $(X_2,p_2)$
are isomorphic pointed PHS for G,
$(X_2,p_2)$
are isomorphic pointed PHS for G,
![]() $p_1$
is a B-point of
$p_1$
is a B-point of
![]() $X_1$
if and only if
$X_1$
if and only if
![]() $p_2$
is a B-point of
$p_2$
is a B-point of
![]() $X_2$
.
$X_2$
.
Definition 3.5. The A-isomorphism classes of A-definable pointed PHS for G whose representatives all have a B-point as their basepoint form a sub-pointed set of
![]() $\operatorname {\mathrm {P}}_{\operatorname {\mathrm {def}}}(M/A,G(M))$
which we will denote
$\operatorname {\mathrm {P}}_{\operatorname {\mathrm {def}}}(M/A,G(M))$
which we will denote
![]() $\operatorname {\mathrm {P}}_{\operatorname {\mathrm {def}},*}(B/A,G(B))$
.
$\operatorname {\mathrm {P}}_{\operatorname {\mathrm {def}},*}(B/A,G(B))$
.
In addition, the set of A-isomorphism classes of A-definable PHS for G whose representatives all contain a B-point form a sub-pointed set of
![]() $\operatorname {\mathrm {P}}_{\operatorname {\mathrm {def}}}(M/A,G(M))$
which we denote
$\operatorname {\mathrm {P}}_{\operatorname {\mathrm {def}}}(M/A,G(M))$
which we denote
![]() $\operatorname {\mathrm {P}}_{\operatorname {\mathrm {def}}}(B/A,G(B))$
.
$\operatorname {\mathrm {P}}_{\operatorname {\mathrm {def}}}(B/A,G(B))$
.
Note that the identity of G is an A-point, so contained in B. So the isomorphism class containing G is in
![]() $\operatorname {\mathrm {P}}_{\operatorname {\mathrm {def}}}(B/A,G(B))$
. Note also that the isomorphism class of
$\operatorname {\mathrm {P}}_{\operatorname {\mathrm {def}}}(B/A,G(B))$
. Note also that the isomorphism class of
![]() $(G,e)$
is in
$(G,e)$
is in
![]() $\operatorname {\mathrm {P}}_{\operatorname {\mathrm {def}},*}(B/A,G(B))$
. Thus
$\operatorname {\mathrm {P}}_{\operatorname {\mathrm {def}},*}(B/A,G(B))$
. Thus
![]() $\operatorname {\mathrm {P}}_{\operatorname {\mathrm {def}},*}(B/A,G(B))$
and
$\operatorname {\mathrm {P}}_{\operatorname {\mathrm {def}},*}(B/A,G(B))$
and
![]() $\operatorname {\mathrm {P}}_{\operatorname {\mathrm {def}}}(B/A,G(B))$
are nonempty.
$\operatorname {\mathrm {P}}_{\operatorname {\mathrm {def}}}(B/A,G(B))$
are nonempty.
Remark 3.6. As B is required to be
![]() $\operatorname {\mathrm {dcl}}$
-closed, if X is any A-definable right PHS for G with a B-point, then restricting the action of G on X to B-points, we see that
$\operatorname {\mathrm {dcl}}$
-closed, if X is any A-definable right PHS for G with a B-point, then restricting the action of G on X to B-points, we see that
![]() $X(B)$
is an abstract right PHS for
$X(B)$
is an abstract right PHS for
![]() $G(B)$
equivariant with respect to the left action of
$G(B)$
equivariant with respect to the left action of
![]() $\operatorname {\mathrm {Aut}}(B/A)$
.
$\operatorname {\mathrm {Aut}}(B/A)$
.
We now refine Proposition 1.1 to describe the setting of normal extensions of parameters.
Proposition 3.7. There is a natural isomorphism
between the set of cohomology classes of definable cocycles from
![]() $\operatorname {\mathrm {Aut}}(B/A)$
to
$\operatorname {\mathrm {Aut}}(B/A)$
to
![]() $G(B)$
and the pointed set of isomorphism classes of A-definable PHS X for G which contain a B-point.
$G(B)$
and the pointed set of isomorphism classes of A-definable PHS X for G which contain a B-point.
The following lemmas trace the constructions (from [Reference Pillay2]) of a cocycle in
![]() $\operatorname {\mathrm {Z}}^{1}_{\operatorname {\mathrm {def}}}(M/A,G(M))$
from a pointed PHS in
$\operatorname {\mathrm {Z}}^{1}_{\operatorname {\mathrm {def}}}(M/A,G(M))$
from a pointed PHS in
![]() $\operatorname {\mathrm {P}}_{\operatorname {\mathrm {def}},*}(M/A,G(M))$
and vice versa. We check that via these constructions the cocycles in the image of
$\operatorname {\mathrm {P}}_{\operatorname {\mathrm {def}},*}(M/A,G(M))$
and vice versa. We check that via these constructions the cocycles in the image of
![]() $\operatorname {\mathrm {Z}}^{1}_{\operatorname {\mathrm {def}}}(B/A,G(B))$
under the map of Lemma 3.4 corresponds to
$\operatorname {\mathrm {Z}}^{1}_{\operatorname {\mathrm {def}}}(B/A,G(B))$
under the map of Lemma 3.4 corresponds to
![]() $\operatorname {\mathrm {P}}_{\operatorname {\mathrm {def}},*}(B/A,G(B))$
, that is, cocycles whose definability parameters come from B correspond exactly to pointed PHSs which have a B-point as their basepoint.
$\operatorname {\mathrm {P}}_{\operatorname {\mathrm {def}},*}(B/A,G(B))$
, that is, cocycles whose definability parameters come from B correspond exactly to pointed PHSs which have a B-point as their basepoint.
Lemma 3.8. An A-definable pointed PHS
![]() $(X,p)$
for G with
$(X,p)$
for G with
![]() $p \in X(B)$
gives rise to a cocycle
$p \in X(B)$
gives rise to a cocycle
![]() $\varphi :\operatorname {\mathrm {Aut}}(M/A) \to G(M)$
which has the B-point
$\varphi :\operatorname {\mathrm {Aut}}(M/A) \to G(M)$
which has the B-point
![]() $p \in X(B)$
as its definability parameter.
$p \in X(B)$
as its definability parameter.
Proof. As
![]() $p \in X(B)$
,
$p \in X(B)$
,
![]() $\sigma (p) \in X(B)$
. We define
$\sigma (p) \in X(B)$
. We define
![]() $\varphi $
by sending
$\varphi $
by sending
![]() $\sigma \in \operatorname {\mathrm {Aut}}(B/A)$
to the unique
$\sigma \in \operatorname {\mathrm {Aut}}(B/A)$
to the unique
![]() $g_\sigma \in G(B)$
such that
$g_\sigma \in G(B)$
such that
![]() $\sigma (p) = pg_\sigma $
. The cocycle condition is easily checked. Let
$\sigma (p) = pg_\sigma $
. The cocycle condition is easily checked. Let
![]() $\Gamma (\mu )(\bar {x},\bar {z},\bar {y})$
define the graph of the definable action
$\Gamma (\mu )(\bar {x},\bar {z},\bar {y})$
define the graph of the definable action
![]() $\mu :X \times G \to X$
. Let
$\mu :X \times G \to X$
. Let
![]() $h(\bar {x},\bar {y}) = \bar {z}$
be the definable function whose graph is
$h(\bar {x},\bar {y}) = \bar {z}$
be the definable function whose graph is
![]() $\Gamma (\mu )(\bar {x},\bar {z},\bar {y})$
. Then
$\Gamma (\mu )(\bar {x},\bar {z},\bar {y})$
. Then
![]() $h(\bar {x},\bar {y})$
together with the parameter p witnesses the definability condition.
$h(\bar {x},\bar {y})$
together with the parameter p witnesses the definability condition.
Let
![]() $\varphi :\operatorname {\mathrm {Aut}}(M/A) \to G(M)$
be a definable cocycle witnessed by an A-definable function h and definability parameter
$\varphi :\operatorname {\mathrm {Aut}}(M/A) \to G(M)$
be a definable cocycle witnessed by an A-definable function h and definability parameter
![]() $\bar {a}$
from B. Note that as
$\bar {a}$
from B. Note that as
![]() $B \subseteq M$
and M is atomic over A, the type
$B \subseteq M$
and M is atomic over A, the type
![]() $\operatorname {\mathrm {tp}}(\bar {a}/A)$
is isolated and is then given by an A-definable set Z defined by a formula
$\operatorname {\mathrm {tp}}(\bar {a}/A)$
is isolated and is then given by an A-definable set Z defined by a formula
![]() $\theta (\bar {x})$
. The following facts are from [Reference Pillay2].
$\theta (\bar {x})$
. The following facts are from [Reference Pillay2].
Fact 3.9. Let
![]() $\bar {b}$
and
$\bar {b}$
and
![]() $\bar {c}$
be tuples from M having the same type as
$\bar {c}$
be tuples from M having the same type as
![]() $\bar {a}$
over A. Then
$\bar {a}$
over A. Then
![]() $h(\bar {a},\bar {c}) = h(\bar {a},\bar {b})h(\bar {b},\bar {c})$
.
$h(\bar {a},\bar {c}) = h(\bar {a},\bar {b})h(\bar {b},\bar {c})$
.
Fact 3.10. Let
![]() $(\bar {a}_1,g_1)$
and
$(\bar {a}_1,g_1)$
and
![]() $(\bar {a}_2,g_2)$
be elements from
$(\bar {a}_2,g_2)$
be elements from
![]() $Y(M):= Z(M) \times G(M)$
. The binary relation defined by
$Y(M):= Z(M) \times G(M)$
. The binary relation defined by
![]() $h(\bar {a}_1,\bar {a}_2)g_2 = g_1$
is an A-definable equivalence relation on this set. We will denote the equivalence relation by E.
$h(\bar {a}_1,\bar {a}_2)g_2 = g_1$
is an A-definable equivalence relation on this set. We will denote the equivalence relation by E.
Lemma 3.11. The definable cocycle
![]() $\varphi $
, with definability parameter contained in B, gives rise to a pointed PHS for G whose basepoint is a B-point.
$\varphi $
, with definability parameter contained in B, gives rise to a pointed PHS for G whose basepoint is a B-point.
Proof. By EI, the quotient of
![]() $Y = Z \times G$
by E, is again an A-definable set X.
$Y = Z \times G$
by E, is again an A-definable set X.
It is clear that G acts A-definably on the right on Y by multiplication on the right on the G-coordinate. It is easy to see that this action preserves the classes of the equivalence relation and so descends to an action on X: if
![]() $g \in G$
,
$g \in G$
,
![]() $h(\bar {a}_1,\bar {a}_2)g_2 = g_1$
iff
$h(\bar {a}_1,\bar {a}_2)g_2 = g_1$
iff
![]() $h(\bar {a}_1,\bar {a}_2)g_2g = g_1g$
. Similarly, because G is a right torsor for itself, the action is regular: Let
$h(\bar {a}_1,\bar {a}_2)g_2g = g_1g$
. Similarly, because G is a right torsor for itself, the action is regular: Let
![]() $(\bar {a}_1,g_1)$
and
$(\bar {a}_1,g_1)$
and
![]() $(\bar {a}_2,g_2)$
be elements of Y. As
$(\bar {a}_2,g_2)$
be elements of Y. As
![]() $h(\bar {a}_1,\bar {a}_2)$
,
$h(\bar {a}_1,\bar {a}_2)$
,
![]() $g_1$
and
$g_1$
and
![]() $g_2$
are elements of G, there is a unique element
$g_2$
are elements of G, there is a unique element
![]() $g \in G$
such that
$g \in G$
such that
![]() $h(\bar {a}_1,\bar {a}_2)g_2g = g_1$
. That is, g is the unique element such that
$h(\bar {a}_1,\bar {a}_2)g_2g = g_1$
. That is, g is the unique element such that
![]() $(\bar {a}_1,g_1)E(\bar {a}_2,g_2g)$
. We have shown that X is an A-definable PHS for G.
$(\bar {a}_1,g_1)E(\bar {a}_2,g_2g)$
. We have shown that X is an A-definable PHS for G.
Finally, the specified basepoint of X is the E-class of
![]() $(\bar {a},e)$
which lives in
$(\bar {a},e)$
which lives in
![]() $\operatorname {\mathrm {dcl}}^{eq}(B)$
. Note by EI and assumptions,
$\operatorname {\mathrm {dcl}}^{eq}(B)$
. Note by EI and assumptions,
![]() $\operatorname {\mathrm {dcl}}^{eq}(B) = \operatorname {\mathrm {dcl}}(B) = B$
.
$\operatorname {\mathrm {dcl}}^{eq}(B) = \operatorname {\mathrm {dcl}}(B) = B$
.
Before proving Proposition 3.7 we discuss the correspondence of Proposition 1.1. Cocycles
![]() $\varphi :\operatorname {\mathrm {Aut}}(M/A) \to G(M)$
correspond to isomorphism classes of pointed PHSs for G. Cohomology classes of cocycles correspond to isomorphism classes of PHSs for G, that is, cohomologous cocycles correspond to pointed PHSs which are isomorphic as PHSs but not as pointed PHSs: There is an A-definable G-equivariant bijection between the PHSs which is not neccesarily basepoint preserving.
$\varphi :\operatorname {\mathrm {Aut}}(M/A) \to G(M)$
correspond to isomorphism classes of pointed PHSs for G. Cohomology classes of cocycles correspond to isomorphism classes of PHSs for G, that is, cohomologous cocycles correspond to pointed PHSs which are isomorphic as PHSs but not as pointed PHSs: There is an A-definable G-equivariant bijection between the PHSs which is not neccesarily basepoint preserving.
Proof of Proposition 3.7
By Lemma 3.2,
![]() $\operatorname {\mathrm {H}}^1(B/A,G(B))$
injects into the cohomology set
$\operatorname {\mathrm {H}}^1(B/A,G(B))$
injects into the cohomology set
![]() $\operatorname {\mathrm {H}}^1(M/A,G(M))$
. The image of this map is exactly the set of cohomology classes containing a cocycle with definability parameter contained in B.
$\operatorname {\mathrm {H}}^1(M/A,G(M))$
. The image of this map is exactly the set of cohomology classes containing a cocycle with definability parameter contained in B.
By Lemmas 3.6 and 3.9, cocycles with definability parameters contained in B correspond exactly with pointed PHSs for G whose basepoint is a B-point. From the preceding discussion, cocycles which are cohomologous to cocycles with definability parameters from B correspond to pointed PHSs which are isomorphic as PHSs (but not neccesarily as pointed PHS) to PHSs which have a B-point as basepoint, and so themselves must contain a B-point.
We have shown that
![]() $\operatorname {\mathrm {P}}_{\operatorname {\mathrm {def}}}(B/A,G(B))$
, the pointed set of isomorphism classes of PHSs whose representatives contain a B-point, is isomorphic as a pointed set to
$\operatorname {\mathrm {P}}_{\operatorname {\mathrm {def}}}(B/A,G(B))$
, the pointed set of isomorphism classes of PHSs whose representatives contain a B-point, is isomorphic as a pointed set to
![]() $\operatorname {\mathrm {H}}^{1}_{\operatorname {\mathrm {def}}}(B/A,G(B))$
.
$\operatorname {\mathrm {H}}^{1}_{\operatorname {\mathrm {def}}}(B/A,G(B))$
.
We conclude this section by giving an alternative definition of a definable cocycle from
![]() $\operatorname {\mathrm {Aut}}(B/A)$
to
$\operatorname {\mathrm {Aut}}(B/A)$
to
![]() $G(B)$
using notions introduced in [Reference Pillay3] and remark on the various definitions of cocycles appearing in the literature.
$G(B)$
using notions introduced in [Reference Pillay3] and remark on the various definitions of cocycles appearing in the literature.
Recall from [Reference Pillay3] that a set
![]() $Y \subseteq \operatorname {\mathrm {Aut}}(M/A)$
is called definable if there is an A-formula
$Y \subseteq \operatorname {\mathrm {Aut}}(M/A)$
is called definable if there is an A-formula
![]() $\varphi (\bar {x},\bar {y})$
and a tuple
$\varphi (\bar {x},\bar {y})$
and a tuple
![]() $\bar {b}$
from M such that
$\bar {b}$
from M such that
Furthermore, let X be an A-definable set. We say that
![]() $\Lambda $
, a subset of
$\Lambda $
, a subset of
![]() $\operatorname {\mathrm {Aut}}(M/A)\times X(M)$
, is definable if there is an A-formula
$\operatorname {\mathrm {Aut}}(M/A)\times X(M)$
, is definable if there is an A-formula
![]() $\varphi (\bar {x},\bar {y},\bar {z})$
and a tuple
$\varphi (\bar {x},\bar {y},\bar {z})$
and a tuple
![]() $\bar {b}$
from M such that
$\bar {b}$
from M such that
The following statement is [Reference Pillay3, Lemma 3.5]. It gives either an alternative definition or a characterization of definable cocycles: Let
![]() $\varphi $
be a function from
$\varphi $
be a function from
![]() $\operatorname {\mathrm {Aut}}(M/A)$
to G. Then there is an A-definable function
$\operatorname {\mathrm {Aut}}(M/A)$
to G. Then there is an A-definable function
![]() $h(\bar {x},\bar {y})$
and a tuple
$h(\bar {x},\bar {y})$
and a tuple
![]() $\bar {b}$
from M such that for all
$\bar {b}$
from M such that for all
![]() $\sigma \in \operatorname {\mathrm {Aut}}(M/A) \varphi (\sigma ) = h(\bar {b},\sigma (\bar {b}))$
if and only if the graph of
$\sigma \in \operatorname {\mathrm {Aut}}(M/A) \varphi (\sigma ) = h(\bar {b},\sigma (\bar {b}))$
if and only if the graph of
![]() $\varphi $
is definable in the above sense.
$\varphi $
is definable in the above sense.
We now give a similar statement in the setting of a normal extension. In [Reference Pillay3], the following definitions (or a slight variation of them depending on the version) are given.
Definition 3.12. A set
![]() $Y \subseteq \operatorname {\mathrm {Aut}}(B/A)$
is called definable if there is an A-formula
$Y \subseteq \operatorname {\mathrm {Aut}}(B/A)$
is called definable if there is an A-formula
![]() $\varphi (\bar {x},\bar {y})$
and a tuple
$\varphi (\bar {x},\bar {y})$
and a tuple
![]() $\bar {b}$
from B such that
$\bar {b}$
from B such that
Furthermore, let X be an A-definable set. We say that
![]() $\Lambda $
, a subset of
$\Lambda $
, a subset of
![]() $\operatorname {\mathrm {Aut}}(B/A)\times X(M)$
, is definable if there is an A-formula
$\operatorname {\mathrm {Aut}}(B/A)\times X(M)$
, is definable if there is an A-formula
![]() $\varphi (\bar {x},\bar {y},\bar {z})$
and a tuple
$\varphi (\bar {x},\bar {y},\bar {z})$
and a tuple
![]() $\bar {b}$
from B such that
$\bar {b}$
from B such that
This gives an alternative characterization of the cocycles introduced in the beginning of this section.
Lemma 3.13. Let
![]() $\varphi $
be a function from
$\varphi $
be a function from
![]() $\operatorname {\mathrm {Aut}}(B/A)$
to
$\operatorname {\mathrm {Aut}}(B/A)$
to
![]() $G(B)$
. Then there is an A-definable function
$G(B)$
. Then there is an A-definable function
![]() $h(\bar {x},\bar {y})$
and a tuple
$h(\bar {x},\bar {y})$
and a tuple
![]() $\bar {b}$
from B such that for all
$\bar {b}$
from B such that for all
![]() $\sigma \in \operatorname {\mathrm {Aut}}(B/A) \varphi (\sigma ) = h(\bar {b},\sigma (\bar {b}))$
if and only if the graph of
$\sigma \in \operatorname {\mathrm {Aut}}(B/A) \varphi (\sigma ) = h(\bar {b},\sigma (\bar {b}))$
if and only if the graph of
![]() $\varphi $
is definable in the sense of the previous definition.
$\varphi $
is definable in the sense of the previous definition.
We adapt the proof of Lemma 3.5 of [Reference Pillay3].
Proof. Suppose that for
![]() $\varphi :\operatorname {\mathrm {Aut}}(B/A) \to G(B)$
, there is a tuple
$\varphi :\operatorname {\mathrm {Aut}}(B/A) \to G(B)$
, there is a tuple
![]() $\bar {b}$
from B and definable function
$\bar {b}$
from B and definable function
![]() $h(\bar {x},\bar {y}) = \bar {z}$
such that for all
$h(\bar {x},\bar {y}) = \bar {z}$
such that for all
![]() $\sigma \in \operatorname {\mathrm {Aut}}(B/A)$
,
$\sigma \in \operatorname {\mathrm {Aut}}(B/A)$
,
![]() $\varphi (\sigma ) = h(\bar {b},\sigma (\bar {b}))$
. Let
$\varphi (\sigma ) = h(\bar {b},\sigma (\bar {b}))$
. Let
![]() $\Gamma (h)(\bar {x},\bar {y},\bar {z})$
be the graph of h. Now,
$\Gamma (h)(\bar {x},\bar {y},\bar {z})$
be the graph of h. Now,
![]() $(\sigma ,g) \in \Gamma (\varphi )$
, the graph of
$(\sigma ,g) \in \Gamma (\varphi )$
, the graph of
![]() $\varphi $
, iff
$\varphi $
, iff
![]() $\varphi (\sigma ) = g$
iff
$\varphi (\sigma ) = g$
iff
![]() $ M \models h(\bar {b},\sigma (\bar {b})) = g$
. So the graph of
$ M \models h(\bar {b},\sigma (\bar {b})) = g$
. So the graph of
![]() $\varphi $
is definable via
$\varphi $
is definable via
![]() $\Gamma (h)(\bar {x},\bar {y},\bar {z})$
and parameter
$\Gamma (h)(\bar {x},\bar {y},\bar {z})$
and parameter
![]() $\bar {b}$
.
$\bar {b}$
.
Suppose now that
![]() $\varphi :\operatorname {\mathrm {Aut}}(B/A) \to G(B)$
is a function whose graph is definable via an A-formula
$\varphi :\operatorname {\mathrm {Aut}}(B/A) \to G(B)$
is a function whose graph is definable via an A-formula
![]() $\psi (\bar {x},\bar {y}, \bar {z})$
and parameter
$\psi (\bar {x},\bar {y}, \bar {z})$
and parameter
![]() $\bar {b}$
from B so that
$\bar {b}$
from B so that
Let
![]() $\theta (\bar {x})$
isolate the type
$\theta (\bar {x})$
isolate the type
![]() $\operatorname {\mathrm {tp}}(\bar {b}/A)$
and let Z be the associated definable set of realizations of this type. We want to produce a definable function from
$\operatorname {\mathrm {tp}}(\bar {b}/A)$
and let Z be the associated definable set of realizations of this type. We want to produce a definable function from
![]() $h:Z^2 \to G$
satisfying the definability condition of Definition 3.3 (ii).
$h:Z^2 \to G$
satisfying the definability condition of Definition 3.3 (ii).
Let
![]() $\bar {b}'$
realize the type of
$\bar {b}'$
realize the type of
![]() $\bar {b}$
over A. By the strong
$\bar {b}$
over A. By the strong
![]() $\omega $
-homogeneity of M over A and normality of B, there is an automorphism
$\omega $
-homogeneity of M over A and normality of B, there is an automorphism
![]() $\sigma \in \operatorname {\mathrm {Aut}}(B/A)$
with
$\sigma \in \operatorname {\mathrm {Aut}}(B/A)$
with
![]() $\sigma (\bar {b}) = \bar {b}'$
. Let
$\sigma (\bar {b}) = \bar {b}'$
. Let
![]() $g = \varphi (\sigma )$
. Then by the definability of the graph of
$g = \varphi (\sigma )$
. Then by the definability of the graph of
![]() $\varphi $
,
$\varphi $
,
![]() $M \models \psi (\bar {b},\sigma (\bar {b}),g)$
and so
$M \models \psi (\bar {b},\sigma (\bar {b}),g)$
and so
![]() $M \models \psi (\bar {b},\bar {b}',g)$
. So for any realization
$M \models \psi (\bar {b},\bar {b}',g)$
. So for any realization
![]() $\bar {b}'$
of
$\bar {b}'$
of
![]() $\operatorname {\mathrm {tp}}(\bar {b}/A)$
there is at least one
$\operatorname {\mathrm {tp}}(\bar {b}/A)$
there is at least one
![]() $g \in G(B)$
with
$g \in G(B)$
with
![]() $M \models \psi (\bar {b},\bar {b'},g)$
. Also, let
$M \models \psi (\bar {b},\bar {b'},g)$
. Also, let
![]() $g,g' \in G(M)$
such that for some
$g,g' \in G(M)$
such that for some
![]() $\bar {b}'$
realizing
$\bar {b}'$
realizing
![]() $\operatorname {\mathrm {tp}}(\bar {b}/A)$
we have
$\operatorname {\mathrm {tp}}(\bar {b}/A)$
we have
![]() $M \models \psi (\bar {b},\bar {b}',g)$
and
$M \models \psi (\bar {b},\bar {b}',g)$
and
![]() $M \models \psi (\bar {b},\bar {b}',g')$
. Again, via strong
$M \models \psi (\bar {b},\bar {b}',g')$
. Again, via strong
![]() $\omega $
-homogeneity and normality let
$\omega $
-homogeneity and normality let
![]() $\sigma (\bar {b}) = \bar {b}'$
. Then
$\sigma (\bar {b}) = \bar {b}'$
. Then
![]() $M \models \psi (\bar {b},\sigma (\bar {b}),g)$
and
$M \models \psi (\bar {b},\sigma (\bar {b}),g)$
and
![]() $M \models \psi (\bar {b},\sigma (\bar {b}),g')$
. By the definability of
$M \models \psi (\bar {b},\sigma (\bar {b}),g')$
. By the definability of
![]() $\varphi $
we have
$\varphi $
we have
![]() $(\sigma ,g) \in \Gamma (\varphi )$
and
$(\sigma ,g) \in \Gamma (\varphi )$
and
![]() $(\sigma ,g') \in \Gamma (\varphi )$
and since
$(\sigma ,g') \in \Gamma (\varphi )$
and since
![]() $\varphi $
is a function,
$\varphi $
is a function,
![]() $g = g'$
. So there is exactly one
$g = g'$
. So there is exactly one
![]() $g \in G(M)$
such that
$g \in G(M)$
such that
![]() $M \models \psi (\bar {b},\bar {b}',\bar {g})$
for any realization of
$M \models \psi (\bar {b},\bar {b}',\bar {g})$
for any realization of
![]() $\operatorname {\mathrm {tp}}(\bar {b}/A)$
. We therefore have that
$\operatorname {\mathrm {tp}}(\bar {b}/A)$
. We therefore have that
Also as
![]() $\theta (\bar {x})$
isolates the type of
$\theta (\bar {x})$
isolates the type of
![]() $\bar {b}$
, we have
$\bar {b}$
, we have
So
![]() $\theta (\bar {y})\wedge \theta (\bar {x}) \wedge \psi (\bar {x},\bar {y},\bar {z})$
is the graph of the desired definable function
$\theta (\bar {y})\wedge \theta (\bar {x}) \wedge \psi (\bar {x},\bar {y},\bar {z})$
is the graph of the desired definable function
![]() $h: Z^2 \to G$
with parameter
$h: Z^2 \to G$
with parameter
![]() $\bar {b}$
from B satisfying the definability condition of Definition 3.3 (ii).
$\bar {b}$
from B satisfying the definability condition of Definition 3.3 (ii).
Remark 3.14. Concerning the various definitions of cocycles:
-
1. In the algebraic setting of [Reference Serre5], cocycles are defined to be continuous. If
 $\operatorname {\mathrm {Aut}}(M/A)$
is given the usual structure of a topological group where a neighborhood base of the identity is the set of stabilizers of finite tuples from M, and
$\operatorname {\mathrm {Aut}}(M/A)$
is given the usual structure of a topological group where a neighborhood base of the identity is the set of stabilizers of finite tuples from M, and
 $G(M)$
is given the discrete topology, then continuity of a cocycle
$G(M)$
is given the discrete topology, then continuity of a cocycle
 $\varphi $
is equivalent the cocycle condition together with the data of an
$\varphi $
is equivalent the cocycle condition together with the data of an
 $\operatorname {\mathrm {Aut}}(M/A)$
-invariant function
$\operatorname {\mathrm {Aut}}(M/A)$
-invariant function
 $h(\bar {x},\bar {y})$
and a tuple
$h(\bar {x},\bar {y})$
and a tuple
 $\bar {a}$
from M such that for any
$\bar {a}$
from M such that for any
 $\sigma \in \operatorname {\mathrm {Aut}}(M/A)$
,
$\sigma \in \operatorname {\mathrm {Aut}}(M/A)$
,
 $\varphi (\sigma ) = h(\bar {a},\sigma (\bar {a}))$
. This observation is contained implicitly in [Reference Pillay2, Lemma 2.6]. This gives some motivation for the definition of a definable cocycle.
$\varphi (\sigma ) = h(\bar {a},\sigma (\bar {a}))$
. This observation is contained implicitly in [Reference Pillay2, Lemma 2.6]. This gives some motivation for the definition of a definable cocycle.In
 $ACF_0$
, for
$ACF_0$
, for
 $M = \operatorname {\mathrm {acl}}(A)$
the function
$M = \operatorname {\mathrm {acl}}(A)$
the function
 $h(\bar {x},\bar {y})$
is
$h(\bar {x},\bar {y})$
is
 $\operatorname {\mathrm {Aut}}(M/A)$
-invariant if and only if it is A-definable so “invariant” and definable cocycles coincide. That is, at the level of cocycles,
$\operatorname {\mathrm {Aut}}(M/A)$
-invariant if and only if it is A-definable so “invariant” and definable cocycles coincide. That is, at the level of cocycles,
 $Z^{1}_{\operatorname {\mathrm {def}}}$
in the setting of
$Z^{1}_{\operatorname {\mathrm {def}}}$
in the setting of
 $ACF_0$
and
$ACF_0$
and
 $Z^1$
coincide.
$Z^1$
coincide. -
2. Kolchin’s constrained cohomology is defined in terms of what he calls constrained cocycles, satisfy a generalization of the continuity condition. He shows that these are closely connected to another set of cocycles called differential rational cocycles whose definition is closer to the definability data definition. The key point, see [Reference Pillay2, Remark 2.8(ii)], is that despite the fact that the set of constrained cocycles defined by Kolchin,
 $Z^1_{\Delta }$
, is a priori slightly different than the set of definable cocycles specialized to the theory
$Z^1_{\Delta }$
, is a priori slightly different than the set of definable cocycles specialized to the theory
 $DCF_0$
,
$DCF_0$
,
 $Z^1_{\operatorname {\mathrm {def}}}$
, the resulting sets of cohomology classes both classify differential algebraic PHSs and so
$Z^1_{\operatorname {\mathrm {def}}}$
, the resulting sets of cohomology classes both classify differential algebraic PHSs and so
 $H^1_{\operatorname {\mathrm {def}}}$
for the theory
$H^1_{\operatorname {\mathrm {def}}}$
for the theory
 $DCF_0$
and
$DCF_0$
and
 $H^1_{\Delta }$
are equivalent i.e., isomorphic as pointed sets.
$H^1_{\Delta }$
are equivalent i.e., isomorphic as pointed sets. -
3. We also remark that Kolchin suppresses the set of rational points on the coefficients in his notation, writing
 $H^1_\Delta (L/K,G)$
instead of
$H^1_\Delta (L/K,G)$
instead of
 $H^1_\Delta (L/K,G(L))$
for example.
$H^1_\Delta (L/K,G(L))$
for example.
4 The short exact sequence in definable Galois cohomology
In this section we show that a short exact sequence of automorphism groups arising from a normal intermediate extension of parameters induces a short exact sequence in definable Galois cohomology.
We will retain the same assumptions on M, A, T, and G from the previous sections. Our statement here is slightly more general than that of the introduction; we generalize M in the earlier statement to an additional intermediate normal extension C.
Let
![]() $A \subseteq B \subseteq C \subseteq M$
with B and C normal in M,
$A \subseteq B \subseteq C \subseteq M$
with B and C normal in M,
![]() $\operatorname {\mathrm {dcl}}^{eq}$
-closed, such that every elementary permutation of either B or C fixing A lifts to an automorphism of M and such that M is atomic and strongly
$\operatorname {\mathrm {dcl}}^{eq}$
-closed, such that every elementary permutation of either B or C fixing A lifts to an automorphism of M and such that M is atomic and strongly
![]() $\omega $
-homogeneous over both B and C.
$\omega $
-homogeneous over both B and C.
Definition 4.1. Let
![]() $\sigma \in \operatorname {\mathrm {Aut}}(C/A)$
. Let
$\sigma \in \operatorname {\mathrm {Aut}}(C/A)$
. Let
![]() $\varphi \in \operatorname {\mathrm {Z}}^{1}_{\operatorname {\mathrm {def}}}(C/B,G(C))$
be a definable cocycle. Let
$\varphi \in \operatorname {\mathrm {Z}}^{1}_{\operatorname {\mathrm {def}}}(C/B,G(C))$
be a definable cocycle. Let
![]() $(P,p)$
be a pointed definable PHS representing a class in
$(P,p)$
be a pointed definable PHS representing a class in
![]() $\mathcal {P}_{\operatorname {\mathrm {def}},*}(C/B,G(B))$
. We define the transform of
$\mathcal {P}_{\operatorname {\mathrm {def}},*}(C/B,G(B))$
. We define the transform of
![]() $\varphi $
by
$\varphi $
by
![]() $\sigma $
, denoted
$\sigma $
, denoted
![]() $\sigma (\varphi )$
, to be the map
$\sigma (\varphi )$
, to be the map
for
![]() $\tau \in \operatorname {\mathrm {Aut}}(B/C)$
. We define the the transform of
$\tau \in \operatorname {\mathrm {Aut}}(B/C)$
. We define the the transform of
![]() $(P,p)$
by
$(P,p)$
by
![]() $\sigma $
, denoted
$\sigma $
, denoted
![]() $\sigma (P,p)$
to be the definable pointed PHS
$\sigma (P,p)$
to be the definable pointed PHS
![]() $(\sigma (P),\sigma (p))$
.
$(\sigma (P),\sigma (p))$
.
Lemma 4.2. The transform induces a well defined action of
![]() $\operatorname {\mathrm {Aut}}(B/A)$
on both
$\operatorname {\mathrm {Aut}}(B/A)$
on both
![]() $\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(C/B,G(C))$
and
$\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(C/B,G(C))$
and
![]() $\mathcal {P}_{\operatorname {\mathrm {def}}}(C/B,G(C))$
such that the isomorphism between them is equivariant with respect to this action.
$\mathcal {P}_{\operatorname {\mathrm {def}}}(C/B,G(C))$
such that the isomorphism between them is equivariant with respect to this action.
Proof. Let
![]() $(P,p)$
represent an isomorphism class in
$(P,p)$
represent an isomorphism class in
![]() $\mathcal {P}_{\operatorname {\mathrm {def}},*}(C/B,G(B))$
. Let
$\mathcal {P}_{\operatorname {\mathrm {def}},*}(C/B,G(B))$
. Let
![]() $\sigma \in \operatorname {\mathrm {Aut}}(C/A)$
. By the normality of B,
$\sigma \in \operatorname {\mathrm {Aut}}(C/A)$
. By the normality of B,
![]() $\sigma (P)$
is still a B-definable PHS for G containing a B-point
$\sigma (P)$
is still a B-definable PHS for G containing a B-point
![]() $\sigma (p)$
.
$\sigma (p)$
.
Let
![]() $(Q,q)$
be B-definably isomorphic as a pointed PHS to
$(Q,q)$
be B-definably isomorphic as a pointed PHS to
![]() $(P,p)$
via
$(P,p)$
via
![]() $\Phi $
. Then again by normality,
$\Phi $
. Then again by normality,
![]() $\sigma (\Phi )$
is a B-definable PHS isomorphism between
$\sigma (\Phi )$
is a B-definable PHS isomorphism between
![]() $(\sigma (Q),\sigma (q))$
and
$(\sigma (Q),\sigma (q))$
and
![]() $(\sigma (P),\sigma (p))$
so the transform is well defined on
$(\sigma (P),\sigma (p))$
so the transform is well defined on
![]() $\mathcal {P}_{\operatorname {\mathrm {def}},*}(C/B,G(B))$
.
$\mathcal {P}_{\operatorname {\mathrm {def}},*}(C/B,G(B))$
.
Let
![]() $(P,p)$
correspond to a definable cocycle
$(P,p)$
correspond to a definable cocycle
![]() $\varphi \in \operatorname {\mathrm {Z}}^{1}_{\operatorname {\mathrm {def}}}(C/B,G(C))$
via Lemma 3.8. We show that the transform of the cocycle
$\varphi \in \operatorname {\mathrm {Z}}^{1}_{\operatorname {\mathrm {def}}}(C/B,G(C))$
via Lemma 3.8. We show that the transform of the cocycle
![]() $\varphi $
by
$\varphi $
by
![]() $\sigma $
is the cocycle corresponding to the transform of
$\sigma $
is the cocycle corresponding to the transform of
![]() $(P,p)$
. Let
$(P,p)$
. Let
![]() $\tau \in \operatorname {\mathrm {Aut}}(C/B)$
. Recall that
$\tau \in \operatorname {\mathrm {Aut}}(C/B)$
. Recall that
![]() $\sigma (p)$
is the base point of
$\sigma (p)$
is the base point of
![]() $\sigma (P)$
, so applying
$\sigma (P)$
, so applying
![]() $\tau $
we obtain
$\tau $
we obtain
 $$ \begin{align*}\tau(\sigma(p)) &= \sigma(\sigma^{-1}(\tau(\sigma(p))))= \sigma(\sigma^{-1}\tau\sigma(p))\\ &= \sigma(p\varphi(\sigma^{-1}\tau\sigma))\\ &= \sigma(p)\sigma(\varphi(\sigma^{-1}\tau\sigma))\\ &= \sigma(p)\sigma(\varphi)(\tau). \end{align*} $$
$$ \begin{align*}\tau(\sigma(p)) &= \sigma(\sigma^{-1}(\tau(\sigma(p))))= \sigma(\sigma^{-1}\tau\sigma(p))\\ &= \sigma(p\varphi(\sigma^{-1}\tau\sigma))\\ &= \sigma(p)\sigma(\varphi(\sigma^{-1}\tau\sigma))\\ &= \sigma(p)\sigma(\varphi)(\tau). \end{align*} $$
So the cocycle corresponding to
![]() $\sigma (P,p)$
is exactly the transform
$\sigma (P,p)$
is exactly the transform
![]() $\sigma (\varphi )$
. It is also then clear that the transform by
$\sigma (\varphi )$
. It is also then clear that the transform by
![]() $\sigma \in \operatorname {\mathrm {Aut}}(C/A)$
depends only on its action on B and therefore descends to an action of
$\sigma \in \operatorname {\mathrm {Aut}}(C/A)$
depends only on its action on B and therefore descends to an action of
![]() $\operatorname {\mathrm {Aut}}(B/A)$
.
$\operatorname {\mathrm {Aut}}(B/A)$
.
A short computation shows that if
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
in
$\psi $
in
![]() $Z^{1}_{\operatorname {\mathrm {def}}}(C/B,G(C))$
are cohomologous via
$Z^{1}_{\operatorname {\mathrm {def}}}(C/B,G(C))$
are cohomologous via
![]() $g \in G(C)$
, then
$g \in G(C)$
, then
![]() $\sigma (\varphi )$
and
$\sigma (\varphi )$
and
![]() $\sigma (\psi )$
in
$\sigma (\psi )$
in
![]() $Z^{1}_{\operatorname {\mathrm {def}}}(C/B,G(C))$
are cohomologous via
$Z^{1}_{\operatorname {\mathrm {def}}}(C/B,G(C))$
are cohomologous via
![]() $\sigma (g) \in G(C)$
: Let
$\sigma (g) \in G(C)$
: Let
![]() $\varphi (\tau ) = g^{-1}\psi (\tau )\tau (g)$
. Then
$\varphi (\tau ) = g^{-1}\psi (\tau )\tau (g)$
. Then
 $$ \begin{align*} \sigma(\varphi)(\tau) &= \sigma(\varphi(\sigma^{-1}\tau\sigma))\\&= \sigma(g^{-1}\psi(\sigma^{-1}\tau\sigma)\sigma^{-1}\tau\sigma(g)))\\ &= \sigma(g^{-1})\sigma(\psi(\sigma^{-1}\tau\sigma)\tau\sigma(g)\\ &= \sigma(g^{-1})\sigma(\psi)(\tau)\tau(\sigma(g)). \end{align*} $$
$$ \begin{align*} \sigma(\varphi)(\tau) &= \sigma(\varphi(\sigma^{-1}\tau\sigma))\\&= \sigma(g^{-1}\psi(\sigma^{-1}\tau\sigma)\sigma^{-1}\tau\sigma(g)))\\ &= \sigma(g^{-1})\sigma(\psi(\sigma^{-1}\tau\sigma)\tau\sigma(g)\\ &= \sigma(g^{-1})\sigma(\psi)(\tau)\tau(\sigma(g)). \end{align*} $$
So
![]() $\operatorname {\mathrm {Aut}}(B/A)$
acts via the transform on
$\operatorname {\mathrm {Aut}}(B/A)$
acts via the transform on
![]() $\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(C/B,G(C))$
and
$\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(C/B,G(C))$
and
![]() $\mathcal {P}_{\operatorname {\mathrm {def}}}(C/B,G(C))$
equivariantly with respect to the isomorphism between them.
$\mathcal {P}_{\operatorname {\mathrm {def}}}(C/B,G(C))$
equivariantly with respect to the isomorphism between them.
Theorem 4.3. The short exact sequence
induces a short exact sequence in definable Galois cohomology
Proof. Let
![]() $\varphi $
be a definable cocycle from
$\varphi $
be a definable cocycle from
![]() $\operatorname {\mathrm {Aut}}(B/A)$
to
$\operatorname {\mathrm {Aut}}(B/A)$
to
![]() $G(B)$
with definability data h and a. Let
$G(B)$
with definability data h and a. Let
![]() $\pi :\operatorname {\mathrm {Aut}}(C/A) \to \operatorname {\mathrm {Aut}}(B/A)$
be the quotient map. As in the proof of Lemma 3.2, we define a map from
$\pi :\operatorname {\mathrm {Aut}}(C/A) \to \operatorname {\mathrm {Aut}}(B/A)$
be the quotient map. As in the proof of Lemma 3.2, we define a map from
![]() $Z^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
to
$Z^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
to
![]() $Z^1_{\operatorname {\mathrm {def}}}(C/A,G(C))$
by sending
$Z^1_{\operatorname {\mathrm {def}}}(C/A,G(C))$
by sending
![]() $\varphi $
to
$\varphi $
to
![]() $\varphi \circ \pi $
. Now
$\varphi \circ \pi $
. Now
![]() $\varphi \circ \pi $
is still a cocycle witnessed by the same definability data. Since
$\varphi \circ \pi $
is still a cocycle witnessed by the same definability data. Since
![]() $\pi $
is surjective, this map on cocycles is injective. Let
$\pi $
is surjective, this map on cocycles is injective. Let
![]() $\varphi _1$
and
$\varphi _1$
and
![]() $\varphi _2$
in
$\varphi _2$
in
![]() $Z^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
be cohomologous as witnessed by
$Z^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
be cohomologous as witnessed by
![]() $g \in G(B)$
. As
$g \in G(B)$
. As
![]() $G(B) \subseteq G(C)$
, the same element g witnesses that
$G(B) \subseteq G(C)$
, the same element g witnesses that
![]() $\varphi _1 \circ \pi $
and
$\varphi _1 \circ \pi $
and
![]() $\varphi _2 \circ \pi $
are cohomologous. So the map on cocycles descends to a well defined map on cohomology which we call
$\varphi _2 \circ \pi $
are cohomologous. So the map on cocycles descends to a well defined map on cohomology which we call
![]() $\pi ^1$
.
$\pi ^1$
.
Let
![]() $\varphi _1$
and
$\varphi _1$
and
![]() $\varphi _2$
be cocycles from
$\varphi _2$
be cocycles from
![]() $\operatorname {\mathrm {Aut}}(B/A)$
to
$\operatorname {\mathrm {Aut}}(B/A)$
to
![]() $G(B)$
with definability data
$G(B)$
with definability data
![]() $h_1$
,
$h_1$
,
![]() $\bar {a}_1$
and
$\bar {a}_1$
and
![]() $h_2$
,
$h_2$
,
![]() $\bar {a}_2$
respectively. Suppose that
$\bar {a}_2$
respectively. Suppose that
![]() $\varphi _1 \circ \pi $
and
$\varphi _1 \circ \pi $
and
![]() $\varphi _2\circ \pi $
are cohomologous via
$\varphi _2\circ \pi $
are cohomologous via
![]() $g \in G(C)$
. So for all
$g \in G(C)$
. So for all
![]() $\sigma \in \operatorname {\mathrm {Aut}}(C/A)$
and moreover for all
$\sigma \in \operatorname {\mathrm {Aut}}(C/A)$
and moreover for all
![]() $\sigma \in \operatorname {\mathrm {Aut}}(M/A)$
,
$\sigma \in \operatorname {\mathrm {Aut}}(M/A)$
,
As
![]() $\bar {a}_1$
and
$\bar {a}_1$
and
![]() $\bar {a}_2$
lie in B, when
$\bar {a}_2$
lie in B, when
![]() $\sigma \in \operatorname {\mathrm {Aut}}(M/B)$
,
$\sigma \in \operatorname {\mathrm {Aut}}(M/B)$
,
![]() $h_1(\bar {a}_1,\sigma (\bar {a}_1)) = e$
and
$h_1(\bar {a}_1,\sigma (\bar {a}_1)) = e$
and
![]() $h_2(\bar {a}_2,\sigma (\bar {a}_2)) = e$
, and then
$h_2(\bar {a}_2,\sigma (\bar {a}_2)) = e$
, and then
![]() $g^{-1}\sigma (g) = e$
. Thus g is fixed under all automorphisms of M fixing B. As M is atomic and strongly
$g^{-1}\sigma (g) = e$
. Thus g is fixed under all automorphisms of M fixing B. As M is atomic and strongly
![]() $\omega $
-homogeneous over B, we have
$\omega $
-homogeneous over B, we have
![]() $g \in dcl(B)$
. As
$g \in dcl(B)$
. As
![]() $dcl(B) = B$
, we have that
$dcl(B) = B$
, we have that
![]() $g \in G(B)$
. Then g witnesses that
$g \in G(B)$
. Then g witnesses that
![]() $\varphi _1$
and
$\varphi _1$
and
![]() $\varphi _2$
are cohomologous. Thus the induced map on cohomology,
$\varphi _2$
are cohomologous. Thus the induced map on cohomology,
![]() $\pi ^1$
, is injective.
$\pi ^1$
, is injective.
Let
![]() $\iota :\operatorname {\mathrm {Aut}}(C/B) \to \operatorname {\mathrm {Aut}}(C/A)$
be the inclusion map. Precomposition by
$\iota :\operatorname {\mathrm {Aut}}(C/B) \to \operatorname {\mathrm {Aut}}(C/A)$
be the inclusion map. Precomposition by
![]() $\iota $
gives a map of cocycles from
$\iota $
gives a map of cocycles from
![]() $Z^1_{\operatorname {\mathrm {def}}}(C/A,G(C)) \to Z^1_{\operatorname {\mathrm {def}}}(C/B,G(C))$
which induces a well defined map on cohomology
$Z^1_{\operatorname {\mathrm {def}}}(C/A,G(C)) \to Z^1_{\operatorname {\mathrm {def}}}(C/B,G(C))$
which induces a well defined map on cohomology
![]() $\iota ^1$
: The same definability data witnesses that precomposition gives a map of definable cocycles and the same element of
$\iota ^1$
: The same definability data witnesses that precomposition gives a map of definable cocycles and the same element of
![]() $G(C)$
witnesses the cohomology relation on the restriction of the cocycle. Note that for cocycles in
$G(C)$
witnesses the cohomology relation on the restriction of the cocycle. Note that for cocycles in
![]() $\operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(C/A,G(C))$
, precomposition by
$\operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(C/A,G(C))$
, precomposition by
![]() $\iota $
is equivalent to restriction to
$\iota $
is equivalent to restriction to
![]() $\operatorname {\mathrm {Aut}}(C/B)$
.
$\operatorname {\mathrm {Aut}}(C/B)$
.
We now show that the image of
![]() $\iota ^1$
is contained in the fixed points of the action of
$\iota ^1$
is contained in the fixed points of the action of
![]() $\operatorname {\mathrm {Aut}}(B/A)$
on
$\operatorname {\mathrm {Aut}}(B/A)$
on
![]() $\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(C/B,G(C))$
via the transform. Let
$\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(C/B,G(C))$
via the transform. Let
![]() $\sigma \in \operatorname {\mathrm {Aut}}(C/A)$
be a lift of some
$\sigma \in \operatorname {\mathrm {Aut}}(C/A)$
be a lift of some
![]() $\hat {\sigma } \in \operatorname {\mathrm {Aut}}(B/A)$
. Let
$\hat {\sigma } \in \operatorname {\mathrm {Aut}}(B/A)$
. Let
![]() $\varphi \in \operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(C/A,G(C))$
, we show that the transform
$\varphi \in \operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(C/A,G(C))$
, we show that the transform
![]() $\sigma (\varphi \circ \iota )$
is cohomologous to
$\sigma (\varphi \circ \iota )$
is cohomologous to
![]() $\varphi \circ \iota $
. Let
$\varphi \circ \iota $
. Let
![]() $\tau \in \operatorname {\mathrm {Aut}}(C/B)$
. Then
$\tau \in \operatorname {\mathrm {Aut}}(C/B)$
. Then
 $$ \begin{align*} \sigma(\varphi\circ\iota)(\tau) &= \sigma(\varphi(\sigma^{-1}\tau\sigma))\\ &= \sigma(\varphi(\sigma^{-1}))\sigma(\sigma^{-1}(\varphi(\tau)\tau(\varphi(\sigma))))\\ &= \sigma(\varphi(\sigma^{-1})\varphi(\tau)\tau(\varphi(\sigma)))\\ &= g^{-1}\varphi(\tau)\tau(g) \end{align*} $$
$$ \begin{align*} \sigma(\varphi\circ\iota)(\tau) &= \sigma(\varphi(\sigma^{-1}\tau\sigma))\\ &= \sigma(\varphi(\sigma^{-1}))\sigma(\sigma^{-1}(\varphi(\tau)\tau(\varphi(\sigma))))\\ &= \sigma(\varphi(\sigma^{-1})\varphi(\tau)\tau(\varphi(\sigma)))\\ &= g^{-1}\varphi(\tau)\tau(g) \end{align*} $$
where
![]() $g = \varphi (\sigma ) \in G(C)$
. So the cocycles
$g = \varphi (\sigma ) \in G(C)$
. So the cocycles
![]() $\sigma (\varphi \circ \iota )$
and
$\sigma (\varphi \circ \iota )$
and
![]() $\varphi \circ \iota $
are cohomologous via
$\varphi \circ \iota $
are cohomologous via
![]() $\varphi (\sigma )$
. Hence the image of
$\varphi (\sigma )$
. Hence the image of
![]() $\iota ^1$
is contained in
$\iota ^1$
is contained in
![]() $\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(C/B,G(C))^{\operatorname {\mathrm {Aut}}(B/A)}$
. Note that we really need a class in the image: If
$\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(C/B,G(C))^{\operatorname {\mathrm {Aut}}(B/A)}$
. Note that we really need a class in the image: If
![]() $\varphi $
were an arbitrary cocycle in
$\varphi $
were an arbitrary cocycle in
![]() $\operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(C/B,G(B))$
then while it is true that
$\operatorname {\mathrm {Z}}^1_{\operatorname {\mathrm {def}}}(C/B,G(B))$
then while it is true that
![]() $\sigma ^{-1}\tau \sigma \in \operatorname {\mathrm {Aut}}(C/B)$
,
$\sigma ^{-1}\tau \sigma \in \operatorname {\mathrm {Aut}}(C/B)$
,
![]() $\sigma $
is not necessarily in
$\sigma $
is not necessarily in
![]() $\operatorname {\mathrm {Aut}}(C/B)$
and so we could not conclude that
$\operatorname {\mathrm {Aut}}(C/B)$
and so we could not conclude that
![]() $\varphi (\sigma ^{-1}\tau \sigma ) = \varphi (\sigma ^{-1})\sigma ^{-1}(\varphi (\tau )\tau (\varphi (\sigma )))$
needed for the second equality of the computation.
$\varphi (\sigma ^{-1}\tau \sigma ) = \varphi (\sigma ^{-1})\sigma ^{-1}(\varphi (\tau )\tau (\varphi (\sigma )))$
needed for the second equality of the computation.
Choose a cohomology class from
![]() $\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(C/A,G(C))$
in the image of
$\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(C/A,G(C))$
in the image of
![]() $\pi ^1$
. By definition this class has a representative cocycle
$\pi ^1$
. By definition this class has a representative cocycle
![]() $\varphi $
such that
$\varphi $
such that
![]() $\varphi = \psi \circ \pi $
where
$\varphi = \psi \circ \pi $
where
![]() $\psi \in Z^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
. Then
$\psi \in Z^1_{\operatorname {\mathrm {def}}}(B/A,G(B))$
. Then
![]() $\varphi \circ \iota = \psi \circ \pi \circ \iota $
which is the constant cocycle. Since
$\varphi \circ \iota = \psi \circ \pi \circ \iota $
which is the constant cocycle. Since
![]() $\iota ^1$
is a well defined map on cohomology, the image of the original class must be trivial i.e., cohomologous to the constant cocycle. So the image of
$\iota ^1$
is a well defined map on cohomology, the image of the original class must be trivial i.e., cohomologous to the constant cocycle. So the image of
![]() $\pi ^1$
is contained in the kernel of
$\pi ^1$
is contained in the kernel of
![]() $\iota ^1$
.
$\iota ^1$
.
We now check that the kernel of
![]() $\iota ^1$
is contained in the image of
$\iota ^1$
is contained in the image of
![]() $\pi ^1$
: Choose a cohomology class from
$\pi ^1$
: Choose a cohomology class from
![]() $\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(C/A,G(C))$
in the kernel of
$\operatorname {\mathrm {H}}^1_{\operatorname {\mathrm {def}}}(C/A,G(C))$
in the kernel of
![]() $\iota ^1$
. The first claim is that this class must contain a representative mapping to the constant cocycle: If
$\iota ^1$
. The first claim is that this class must contain a representative mapping to the constant cocycle: If
![]() $\varphi '$
is a representative of a class in the kernel of
$\varphi '$
is a representative of a class in the kernel of
![]() $\iota ^1$
then there is a
$\iota ^1$
then there is a
![]() $g \in G(C)$
such that
$g \in G(C)$
such that
![]() $\forall \sigma \in \operatorname {\mathrm {Aut}}(C/B)$
,
$\forall \sigma \in \operatorname {\mathrm {Aut}}(C/B)$
,
![]() $\varphi '(\sigma ) = g^{-1}\sigma (g)$
. But then
$\varphi '(\sigma ) = g^{-1}\sigma (g)$
. But then
![]() $g\varphi '\sigma (g^{-1})$
is another representative of the class of
$g\varphi '\sigma (g^{-1})$
is another representative of the class of
![]() $\varphi '$
which maps to the constant cocycle.
$\varphi '$
which maps to the constant cocycle.
Let
![]() $\varphi $
be a representative of our cohomology class in the kernel of
$\varphi $
be a representative of our cohomology class in the kernel of
![]() $\iota ^1$
such that
$\iota ^1$
such that
![]() $\varphi \circ \iota $
is the constant cocycle. The cocycle
$\varphi \circ \iota $
is the constant cocycle. The cocycle
![]() $\varphi $
is a map from
$\varphi $
is a map from
![]() $\operatorname {\mathrm {Aut}}(C/A)$
to
$\operatorname {\mathrm {Aut}}(C/A)$
to
![]() $G(C)$
which sends the subgroup
$G(C)$
which sends the subgroup
![]() $\operatorname {\mathrm {Aut}}(C/B)$
to the identity of
$\operatorname {\mathrm {Aut}}(C/B)$
to the identity of
![]() $G(C)$
.
$G(C)$
.
We now show that the definability data for
![]() $\varphi $
can be re-chosen so that the parameter comes from B: Let
$\varphi $
can be re-chosen so that the parameter comes from B: Let
![]() $h(\bar {x},\bar {y})$
,
$h(\bar {x},\bar {y})$
,
![]() $\bar {a}$
be the original definability data for
$\bar {a}$
be the original definability data for
![]() $\varphi $
. Let Z be the A-definable set
$\varphi $
. Let Z be the A-definable set
![]() $\operatorname {\mathrm {tp}}(\bar {a}/A)$
; recall that M is isolated over A. From
$\operatorname {\mathrm {tp}}(\bar {a}/A)$
; recall that M is isolated over A. From
![]() $h(\bar {x},\bar {y})$
and
$h(\bar {x},\bar {y})$
and
![]() $\bar {a}$
, we can produce, as in Lemma 3.11, a pointed PHS for G whose underlying definable set is
$\bar {a}$
, we can produce, as in Lemma 3.11, a pointed PHS for G whose underlying definable set is
![]() $(Z\times G)/E$
where E is the A-definable equivalence relation defined by
$(Z\times G)/E$
where E is the A-definable equivalence relation defined by
![]() $(\bar {a},g)E(\bar {a}',g')$
if
$(\bar {a},g)E(\bar {a}',g')$
if
![]() $h(\bar {a},\bar {a}')g' = g$
. The basepoint of this PHS is the E-class
$h(\bar {a},\bar {a}')g' = g$
. The basepoint of this PHS is the E-class
![]() $({a},e)/E$
which furnishes new definability data for
$({a},e)/E$
which furnishes new definability data for
![]() $\varphi $
as in Lemma 3.8.
$\varphi $
as in Lemma 3.8.
Now, let
![]() $\sigma \in \operatorname {\mathrm {Aut}}(C/B)$
. Then
$\sigma \in \operatorname {\mathrm {Aut}}(C/B)$
. Then
![]() $\sigma ((\bar {a},e)/E) = (\bar {a},e)/E$
as
$\sigma ((\bar {a},e)/E) = (\bar {a},e)/E$
as
![]() $h(\bar {a},\sigma (\bar {a}))e = e$
. So
$h(\bar {a},\sigma (\bar {a}))e = e$
. So
![]() $(\bar {a},e)/E$
is fixed pointwise by the action of
$(\bar {a},e)/E$
is fixed pointwise by the action of
![]() $\operatorname {\mathrm {Aut}}(C/B)$
, so
$\operatorname {\mathrm {Aut}}(C/B)$
, so
![]() $(\bar {a},e)/E \in B$
.
$(\bar {a},e)/E \in B$
.
We may now assume that
![]() $\varphi $
has definability parameter
$\varphi $
has definability parameter
![]() $\bar {a}$
coming from B. As in the proof of Lemma 3.4, the definability condition
$\bar {a}$
coming from B. As in the proof of Lemma 3.4, the definability condition
![]() $\varphi (\sigma ) = h(\bar {a},\sigma (\bar {a}))$
shows
$\varphi (\sigma ) = h(\bar {a},\sigma (\bar {a}))$
shows
![]() $\varphi (\sigma ) \in \operatorname {\mathrm {dcl}}(\bar {a},\sigma (\bar {a}))$
and so by the normality of B and the fact that
$\varphi (\sigma ) \in \operatorname {\mathrm {dcl}}(\bar {a},\sigma (\bar {a}))$
and so by the normality of B and the fact that
![]() $\operatorname {\mathrm {dcl}}(B) = B$
, the image of
$\operatorname {\mathrm {dcl}}(B) = B$
, the image of
![]() $\varphi $
is contained in
$\varphi $
is contained in
![]() $G(B)$
. As the definability parameter is contained in B,
$G(B)$
. As the definability parameter is contained in B,
![]() $\varphi $
descends to a well defined map
$\varphi $
descends to a well defined map
![]() $\tilde {\varphi }$
from
$\tilde {\varphi }$
from
![]() $\operatorname {\mathrm {Aut}}(B/A)$
to
$\operatorname {\mathrm {Aut}}(B/A)$
to
![]() $G(B)$
, and moreover
$G(B)$
, and moreover
![]() $\tilde {\varphi }\circ \pi = \varphi $
. We show that
$\tilde {\varphi }\circ \pi = \varphi $
. We show that
![]() $\tilde {\varphi }$
still satisfies the cocycle condition: Let
$\tilde {\varphi }$
still satisfies the cocycle condition: Let
![]() $\sigma ,\tau \in \operatorname {\mathrm {Aut}}(C/A)$
and
$\sigma ,\tau \in \operatorname {\mathrm {Aut}}(C/A)$
and
![]() $\tilde {\sigma },\tilde {\tau } \in \operatorname {\mathrm {Aut}}(B/A)$
with
$\tilde {\sigma },\tilde {\tau } \in \operatorname {\mathrm {Aut}}(B/A)$
with
![]() $\pi (\sigma ) = \tilde {\sigma }$
and
$\pi (\sigma ) = \tilde {\sigma }$
and
![]() $\pi (\tau ) = \tilde {\tau }$
$\pi (\tau ) = \tilde {\tau }$
 $$ \begin{align*} \tilde{\varphi}(\tilde{\sigma}\tilde{\tau}) &= \varphi(\sigma\tau)\\ &= \varphi(\sigma)\sigma(\varphi(\tau))\\ &= \tilde{\varphi}(\tilde{\sigma})\tilde{\sigma}(\tilde{\varphi}(\tilde{\tau})) \end{align*} $$
$$ \begin{align*} \tilde{\varphi}(\tilde{\sigma}\tilde{\tau}) &= \varphi(\sigma\tau)\\ &= \varphi(\sigma)\sigma(\varphi(\tau))\\ &= \tilde{\varphi}(\tilde{\sigma})\tilde{\sigma}(\tilde{\varphi}(\tilde{\tau})) \end{align*} $$
where the last equality holds because the image of
![]() $\varphi $
is contained in B. The same definability data for
$\varphi $
is contained in B. The same definability data for
![]() $\varphi $
shows that
$\varphi $
shows that
![]() $\tilde {\varphi }$
is a definable cocycle. The class of
$\tilde {\varphi }$
is a definable cocycle. The class of
![]() $\varphi $
is then the image of the class of
$\varphi $
is then the image of the class of
![]() $\tilde {\varphi }$
under
$\tilde {\varphi }$
under
![]() $\pi ^1$
.
$\pi ^1$
.
Acknowledgements
The author would like to thank Anand Pillay for many helpful comments and suggestions, and especially for several discussions which led to a simplification of the material in Section 2. The author would like to thank the referee for suggesting the inclusion of an adaptation of Serre’s transform action on the final term of the short exact sequence.